七年级数学二元一次方程组
文档属性
| 名称 | 七年级数学二元一次方程组 |

|
|
| 格式 | zip | ||
| 文件大小 | 395.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-29 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
二元一次方程组全章复习精讲
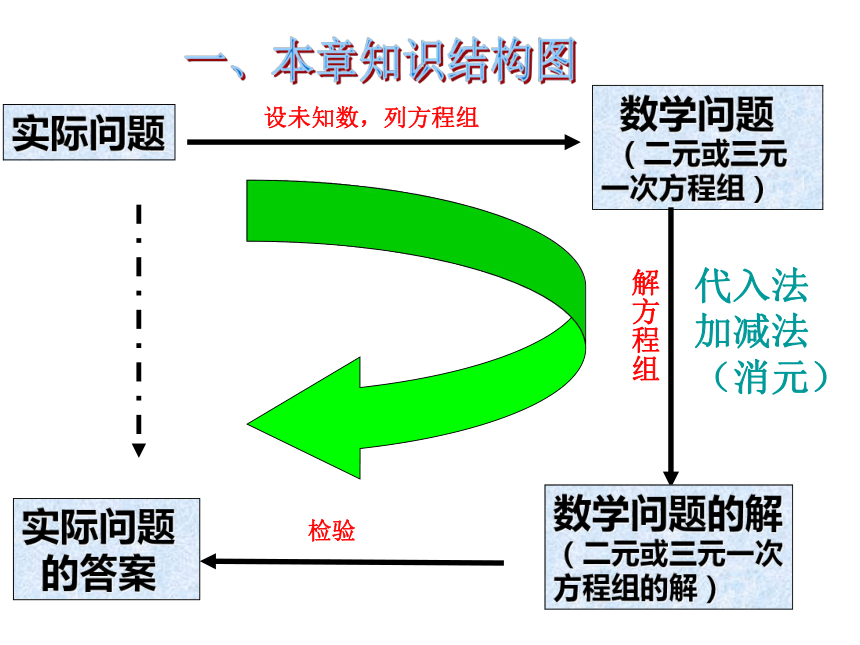
实际问题
设未知数,列方程组
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题
的答案
代入法
加减法
(消元)
二、有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
4.二元一次方程组的解:
使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解.
三、方程组的解法
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——消元
常用方法————代入法和加减法
用代入法解二元一次方程组的步骤:
1.求表达式:从方程组中选一个系数比较简
单的方程,将此方程中的一个未知数,如y,用
含x的代数式表示;
2.把这个含x的代数式代入另一个方程中,
消去y,得到一个关于x的一元一次方程;
3.解一元一次方程,求出x的值;
4.再把求出的x的值 代入变形后的方程,求
出y的值.
用加减法解二元一次方程组的步骤:
1.利用等式性质把一个或两个方程的两边都
乘以适当的数,变换两个方程的某一个未知数
的系数,使其绝对值相等;
2.把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
3.解这个一元一次方程,求得一个未知数的值 ;
4.把所求的这个未知的值代入方程组中较为简
便的一个方程,求出另一个未知数,从而得到方
程的解 .
1.已知: 是关于x、y的二元一次方程,求m、n的值。
2已知: 是方程组
的解,求 的解
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
、知识应用
1.二元一次方程2m+3n=11 ( )
A.任何一对有理数都是它的解.
B.只有两组解.
C.只有两组正整数解.
D.有负整数解.
C
2.方程 中,x、y、z是未知数,若方程为二元一次方程,求a的值。
3.甲、乙两人共同解组 ,甲看错了方程(1)中的a,得到方程组的解为 ,乙看错了方程(2)中的b,得到方程组的解为 ,试计算: 的值。
4.已知关于的方程组 的解是整数,a是正整数,求 a的值。
5.已知,
求
6.已知, 则
7.若方程组 的解
是 , 求方程组
的解。
8.若关于x、y的二元一次方程组
的解互为相反数,求
m的值。
9.解方程组 时,可
由(1)得 (3),然后再将(3)代入(2),4×1-y=5,求得y=-1,从而进一步求得 。
这种方法被称为“整体代入法”,请用这样的方法求方程组 的解。
解法过关
12.用合适的解法解下列方程组:
(1) (2)
同解方程
若关于x,y的方程组
与 有相同的解,求 m,n的值
应用题
1。篮球比赛中都要分出胜负,每队胜一场得2分,负一场得1分,要想在全部22场比赛中得到40分,那么该队胜、负场数分别是多少?
2.甲、乙两人从相距36千米的两地相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇。求甲、乙两人的速度。
应用题
3
.。开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本。
求每支钢笔和每本笔记本的价格。
应用题
4.栖树一群鸦,鸦树不知数,三只栖一树,五只没出处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”诗句中谈到的鸦为 只,树为 棵。
.5.实验中学组织爱心捐款支援灾区活动,
七年级(一)班55名同学共捐款1180元,
捐款情况见下表,表中捐款10元和20元的
人数不小心被墨水污染已经看不清楚,
请你帮助确定表中的数据
捐款(元) 5 10 20 50
人数 6 7
6.2009年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米。
7.双蓉服装店老板到厂家选购A,B两种型号的装,若购进A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B中型号服装8件,需要1880元。求A,B两种型号的服装每件分别多少元?
9.A,B两地相距2400千米,一架飞机从A地顺风飞往B地需2小时40分,从B地逆风飞往A地需3小时,求飞机的速度与风速。
10.两种枕木共300棵,甲种枕木的总重量比乙种枕木的总重量轻1吨。如果每根枕木甲种重46千克,乙种种28千克,两种枕木各多少根?
11,李明家和陈刚家都从甲、乙两供水点购买同样的一种桶装矿泉水,李明家第一季度从甲、乙两供水点分别购买了10桶和6桶,共花费51元;陈刚家第一季度从甲、乙两供水点分别购买了8桶和12桶,且在乙供水点比在甲供水点多花18元钱。若只考虑价格因素,通过计算说明到哪家供水点购买这种桶装矿泉水更便宜些。
12.舒新服装厂生产某种款式的秋装一批,已知每2米的某种布料可做上衣的衣身3个或衣袖5只。现计划用132米这种布料生产这批秋装(不考虑布料的损耗),应分别用多少布料才能使做的衣身和衣袖恰好配套?
13.某商店为了处理积压商品,实行亏本销售,购进的甲、乙商品的原价之和880元,甲种商品按原价打八折,乙种商品按原价打七五折,结果两种商品共亏196元,则甲、乙两种商品的原价分别为 多少?
14.巍巍古寺在山林,不知寺内几多僧,三百六十四只碗,看看用尽不差矣,三人共食一碗饭,四人共吃一碗羹,请问先生明算者,算来寺内几多僧。”题目大意:一寺庙内不知有多少僧人,但饭碗和汤碗共364只,如果3人共用一个饭碗吃饭,或者4人共用一个汤碗喝汤,正好用完所有的碗,问:寺内共有多少僧人?
解的判别式
.关于x,y的二元一次方程组 ,
当满足何条件是,(1)有唯一解;(2)
无解;(3)无数解。
2.若点P(x-y,3x+y)与点Q(-1,-5)关于X轴对称,则x+y=______.
3
3.已知|2x+3y+5|+(3x+2Y-25)2=0,
则x-y=______.
-30
4.若两个多边形的边数之比是2:3,两个多边形的内角和是1980°,求这两个多边形的边数.
6和9
5.方程组 中,x与y的和为
12,求k的值.
解得:K=14
解法1:解这个方程组,得
依题意:x+y=12
所以(2k-6) +(4-k)=12
解法2:根据题意,得
解这个方程组,得k=14
6、解方程组
7、解方程组
8、解方程组
9、分析对话
累死我了!
你还累?这么大的个,才比我多驮了2个。
哼!我从你背上拿来1个,我的包裹数就是你的2倍!
真的?!
它们各驮了多少包裹呢?
10.甲、乙两人练习跑步,如果甲让乙先跑10米,甲跑5秒钟就可追上乙,如果甲让乙先跑2秒,那么甲跑4秒就能追上乙,问甲、乙每秒各跑多少米?
11.一张方桌由一个桌面和四个桌腿组成,如果1立方米木料可制作方桌桌面50个,或制作桌腿300条,现有5立方米木料,请你设计一下,用多少木料做桌面,用多少木料做桌腿,恰好制成方桌多少张?
12、已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元,某中学计划将100500元钱全部用于从该公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该学校选择,并说明理由。
13、一列快车长70米,慢车长80米。若两车同向而行,快车从追上慢车到完全离开慢车所用时间(会车时间)为20秒。两车相向而行,则两车从相遇到离开时间为4秒,求两车每小时各行多少千米?
14.已知方程组 的解
满足2x+3y=6,求m的值。
二元一次方程组全章复习精讲
实际问题
设未知数,列方程组
数学问题
(二元或三元一次方程组)
解方程组
数学问题的解
(二元或三元一次
方程组的解)
检验
实际问题
的答案
代入法
加减法
(消元)
二、有关概念
1.二元一次方程:通过化简后,只有两个未知数,并且两个未知数的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
4.二元一次方程组的解:
使二元一次方程组的两个方程左、右两边的值都相等的两个未知数的值,叫做二元一次方程组的解.
三、方程组的解法
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——消元
常用方法————代入法和加减法
用代入法解二元一次方程组的步骤:
1.求表达式:从方程组中选一个系数比较简
单的方程,将此方程中的一个未知数,如y,用
含x的代数式表示;
2.把这个含x的代数式代入另一个方程中,
消去y,得到一个关于x的一元一次方程;
3.解一元一次方程,求出x的值;
4.再把求出的x的值 代入变形后的方程,求
出y的值.
用加减法解二元一次方程组的步骤:
1.利用等式性质把一个或两个方程的两边都
乘以适当的数,变换两个方程的某一个未知数
的系数,使其绝对值相等;
2.把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
3.解这个一元一次方程,求得一个未知数的值 ;
4.把所求的这个未知的值代入方程组中较为简
便的一个方程,求出另一个未知数,从而得到方
程的解 .
1.已知: 是关于x、y的二元一次方程,求m、n的值。
2已知: 是方程组
的解,求 的解
解三元一次方程组的基本思路与解二元一次方程组的基本思路一样,即
三元一次方程组
消元
二元一次方程组
消元
一元一次方程
、知识应用
1.二元一次方程2m+3n=11 ( )
A.任何一对有理数都是它的解.
B.只有两组解.
C.只有两组正整数解.
D.有负整数解.
C
2.方程 中,x、y、z是未知数,若方程为二元一次方程,求a的值。
3.甲、乙两人共同解组 ,甲看错了方程(1)中的a,得到方程组的解为 ,乙看错了方程(2)中的b,得到方程组的解为 ,试计算: 的值。
4.已知关于的方程组 的解是整数,a是正整数,求 a的值。
5.已知,
求
6.已知, 则
7.若方程组 的解
是 , 求方程组
的解。
8.若关于x、y的二元一次方程组
的解互为相反数,求
m的值。
9.解方程组 时,可
由(1)得 (3),然后再将(3)代入(2),4×1-y=5,求得y=-1,从而进一步求得 。
这种方法被称为“整体代入法”,请用这样的方法求方程组 的解。
解法过关
12.用合适的解法解下列方程组:
(1) (2)
同解方程
若关于x,y的方程组
与 有相同的解,求 m,n的值
应用题
1。篮球比赛中都要分出胜负,每队胜一场得2分,负一场得1分,要想在全部22场比赛中得到40分,那么该队胜、负场数分别是多少?
2.甲、乙两人从相距36千米的两地相向而行,如果甲比乙先走2小时,那么他们在乙出发2.5小时后相遇;如果乙比甲先走2小时,那么他们在甲出发3小时后相遇。求甲、乙两人的速度。
应用题
3
.。开学初,小芳和小亮去学校商店购买学习用品,小芳用18元钱买了1支钢笔和3本笔记本;小亮用31元买了同样的钢笔2支和笔记本5本。
求每支钢笔和每本笔记本的价格。
应用题
4.栖树一群鸦,鸦树不知数,三只栖一树,五只没出处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”诗句中谈到的鸦为 只,树为 棵。
.5.实验中学组织爱心捐款支援灾区活动,
七年级(一)班55名同学共捐款1180元,
捐款情况见下表,表中捐款10元和20元的
人数不小心被墨水污染已经看不清楚,
请你帮助确定表中的数据
捐款(元) 5 10 20 50
人数 6 7
6.2009年北京市生产运营用水和居民家庭用水的总和为5.8亿立方米,其中居民家庭用水比生产运营用水的3倍还多0.6亿立方米,问生产运营用水和居民家庭用水各多少亿立方米。
7.双蓉服装店老板到厂家选购A,B两种型号的装,若购进A种型号服装9件,B种型号服装10件,需要1810元;若购进A种型号服装12件,B中型号服装8件,需要1880元。求A,B两种型号的服装每件分别多少元?
9.A,B两地相距2400千米,一架飞机从A地顺风飞往B地需2小时40分,从B地逆风飞往A地需3小时,求飞机的速度与风速。
10.两种枕木共300棵,甲种枕木的总重量比乙种枕木的总重量轻1吨。如果每根枕木甲种重46千克,乙种种28千克,两种枕木各多少根?
11,李明家和陈刚家都从甲、乙两供水点购买同样的一种桶装矿泉水,李明家第一季度从甲、乙两供水点分别购买了10桶和6桶,共花费51元;陈刚家第一季度从甲、乙两供水点分别购买了8桶和12桶,且在乙供水点比在甲供水点多花18元钱。若只考虑价格因素,通过计算说明到哪家供水点购买这种桶装矿泉水更便宜些。
12.舒新服装厂生产某种款式的秋装一批,已知每2米的某种布料可做上衣的衣身3个或衣袖5只。现计划用132米这种布料生产这批秋装(不考虑布料的损耗),应分别用多少布料才能使做的衣身和衣袖恰好配套?
13.某商店为了处理积压商品,实行亏本销售,购进的甲、乙商品的原价之和880元,甲种商品按原价打八折,乙种商品按原价打七五折,结果两种商品共亏196元,则甲、乙两种商品的原价分别为 多少?
14.巍巍古寺在山林,不知寺内几多僧,三百六十四只碗,看看用尽不差矣,三人共食一碗饭,四人共吃一碗羹,请问先生明算者,算来寺内几多僧。”题目大意:一寺庙内不知有多少僧人,但饭碗和汤碗共364只,如果3人共用一个饭碗吃饭,或者4人共用一个汤碗喝汤,正好用完所有的碗,问:寺内共有多少僧人?
解的判别式
.关于x,y的二元一次方程组 ,
当满足何条件是,(1)有唯一解;(2)
无解;(3)无数解。
2.若点P(x-y,3x+y)与点Q(-1,-5)关于X轴对称,则x+y=______.
3
3.已知|2x+3y+5|+(3x+2Y-25)2=0,
则x-y=______.
-30
4.若两个多边形的边数之比是2:3,两个多边形的内角和是1980°,求这两个多边形的边数.
6和9
5.方程组 中,x与y的和为
12,求k的值.
解得:K=14
解法1:解这个方程组,得
依题意:x+y=12
所以(2k-6) +(4-k)=12
解法2:根据题意,得
解这个方程组,得k=14
6、解方程组
7、解方程组
8、解方程组
9、分析对话
累死我了!
你还累?这么大的个,才比我多驮了2个。
哼!我从你背上拿来1个,我的包裹数就是你的2倍!
真的?!
它们各驮了多少包裹呢?
10.甲、乙两人练习跑步,如果甲让乙先跑10米,甲跑5秒钟就可追上乙,如果甲让乙先跑2秒,那么甲跑4秒就能追上乙,问甲、乙每秒各跑多少米?
11.一张方桌由一个桌面和四个桌腿组成,如果1立方米木料可制作方桌桌面50个,或制作桌腿300条,现有5立方米木料,请你设计一下,用多少木料做桌面,用多少木料做桌腿,恰好制成方桌多少张?
12、已知某电脑公司有A型、B型、C型三种型号的电脑,其价格分别为A型每台6000元,B型每台4000元,C型每台2500元,某中学计划将100500元钱全部用于从该公司购进其中两种不同型号的电脑共36台,请你设计出几种不同的购买方案供该学校选择,并说明理由。
13、一列快车长70米,慢车长80米。若两车同向而行,快车从追上慢车到完全离开慢车所用时间(会车时间)为20秒。两车相向而行,则两车从相遇到离开时间为4秒,求两车每小时各行多少千米?
14.已知方程组 的解
满足2x+3y=6,求m的值。
