浙江省丽水市普通高中2020-2021学年高二下学期期末教学质量监控数学试题 Word版含答案
文档属性
| 名称 | 浙江省丽水市普通高中2020-2021学年高二下学期期末教学质量监控数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 711.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 10:04:30 | ||
图片预览



文档简介
丽水市2020学年第二学期普通高中期末教学质量监控
高二数学 试题卷 2021.7
本试题卷分选择题和非选择题两部分。全卷共5页,选择题部分1至2页,非选择题部分3至5页。满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
第Ⅰ卷 选择题部分(共40分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。
2.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试题卷上。
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,,则
A. B. C. D.
2.双曲线的焦点坐标是
A. B. C. D.
3.某几何体的三视图(单位:cm)如图所示,
则该几何体的体积是(单位:)
A. B.
C. D.
4.已知实数,,,则
A. B. C. D.
5.已知直线,,和平面,,则是的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
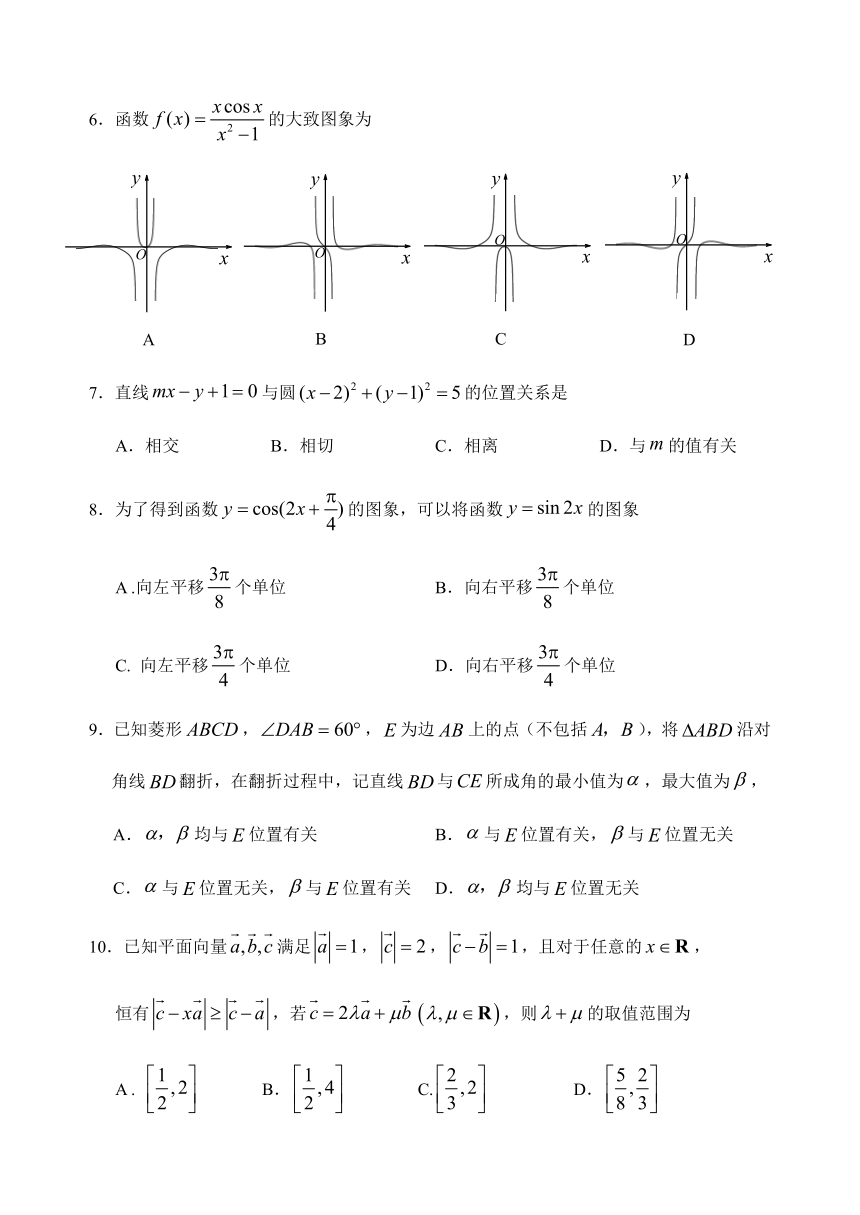
6.函数的大致图象为
7.直线与圆的位置关系是
A.相交 B.相切 C.相离 D.与的值有关
8.为了得到函数的图象,可以将函数的图象
A .向左平移个单位 B.向右平移个单位
C. 向左平移个单位 D.向右平移个单位
9.已知菱形,,为边上的点(不包括),将沿对角线翻折,在翻折过程中,记直线与所成角的最小值为,最大值为,
A.均与位置有关 B.与位置有关,与位置无关
C.与位置无关,与位置有关 D.均与位置无关
10.已知平面向量满足,,,且对于任意的,
恒有,若,则的取值范围为
A . B. C. D.
第Ⅱ卷 非选择题部分(共110分)
注意事项:
1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
2.在答题纸上作图,可先使用2B铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
二、填空题:本题共7小题,其中11-14题每小题6分,15-17题每小题4分,共36分.
11.南宋时期,数学家秦九韶提出利用三角形的三边求面积的公式:如果一个三角形的三边长分别为,那么三角形的面积,后人称之为秦九韶公式.这与古希腊数学家海伦证明的面积公式,
实质是相同的.若在中,,,,则的面积为 ▲ , 的内切圆半径为 ▲ .
12.设变量,满足约束条件,则函数的最大值为 ▲ ,最小值为 ▲ .
13. 已知函数,则 ▲ ;若,则 ▲ .
14. 已知等差数列的首项,公差,且,,成等比数列,则 ▲ .若数列的通项,则的前项和 ▲ .
15.为了测量河对岸两点间的距离,现在沿岸相距的两点处分别测得,
假设四点在同一平面内,
则间的距离为 ▲ .
16. 已知椭圆,过右焦点且斜率为的直线与椭圆相交
于,两点,若,则椭圆的离心率为 ▲ .
17.已知正数满足,则的最大值为 ▲ .
三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)已知函数.
(Ⅰ)求;
(Ⅱ)求在上的值域.
19.(本题满分15分)在四棱锥中,平面平面,底面为直角梯形,,,分别为的中点.
(Ⅰ)证明://平面;
(Ⅱ)求与平面所成角的正弦值.
20.(本题满分15分)已知正项数列的前项的和为,且,
,数列的首项,且满足.
(Ⅰ)求数列,的通项公式;
(Ⅱ)设数列满足,求证:数列的前项和.
21.(本题满分15分)已知抛物线与椭圆有公共焦点,并交于两点.不与轴垂直的直线交抛物线于两点,且的中点在椭圆上,的垂直平分线交轴于点.
(Ⅰ)求抛物线的方程;
(Ⅱ)求点横坐标的取值范围.
22.(本题满分15分)已知函数,,
设.
(Ⅰ)若,且当时,求的最大值;
(Ⅱ)若存在实数,对任意的实数,使得方程恒有四个不同的实数解,求的最小值.
丽水市2020学年第二学期普通高中期末教学质量监控
高二 数学答案
一、选择题:BDDCB;BAACA;
二、填空题:
11.,. 12.,. 13. ,. 14. ,
15.. 16. 17..
18.(本题满分14分)
解:(Ⅰ)
(Ⅱ)
,
所以所求的值域为.
19.(本题满分15分)
(Ⅰ)证明:取AD中点,连接
平面,平面
平面,
平面,平面
平面,
平面平面
平面
(Ⅱ)平面平面
平面平面
平面
平面
以为原点, ,,分别为建立坐标系,设=1.
则,, ,,
,
,,
,
,
是平面的一个法向量,
设与平面所成的角为,
则
20解:(1) 当时,,解得
当时,,
两式相减得:,
又,所以,且
所以
由得
所以
(2)
两式相减得:
所以
所以
21.(本题满分15分)
解: (1)由已知得抛物线的焦点为(1,0),
所以,抛物线方程为
(2)设
两式相减得:
即
所以
即,
由题意得 化得,即
22.解:(1)当时,,
当时,递增,
当时,递减,
所以,当时,.
(a)当时,,为二次方程,不合题意.
(b)当时,,
,
方程无解,不合题意.
(c)当时,,
方程有四个不同的解,等价于直线与的图象有四个不同的交点,
由得在时恒成立,
由得在时恒成立,
对称轴方程,
,,
所以只要
(不合),
综上:的最小值为2.
高二数学 试题卷 2021.7
本试题卷分选择题和非选择题两部分。全卷共5页,选择题部分1至2页,非选择题部分3至5页。满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
第Ⅰ卷 选择题部分(共40分)
注意事项:
1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸上。
2.每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试题卷上。
一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,,则
A. B. C. D.
2.双曲线的焦点坐标是
A. B. C. D.
3.某几何体的三视图(单位:cm)如图所示,
则该几何体的体积是(单位:)
A. B.
C. D.
4.已知实数,,,则
A. B. C. D.
5.已知直线,,和平面,,则是的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.函数的大致图象为
7.直线与圆的位置关系是
A.相交 B.相切 C.相离 D.与的值有关
8.为了得到函数的图象,可以将函数的图象
A .向左平移个单位 B.向右平移个单位
C. 向左平移个单位 D.向右平移个单位
9.已知菱形,,为边上的点(不包括),将沿对角线翻折,在翻折过程中,记直线与所成角的最小值为,最大值为,
A.均与位置有关 B.与位置有关,与位置无关
C.与位置无关,与位置有关 D.均与位置无关
10.已知平面向量满足,,,且对于任意的,
恒有,若,则的取值范围为
A . B. C. D.
第Ⅱ卷 非选择题部分(共110分)
注意事项:
1.用黑色字迹的签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。
2.在答题纸上作图,可先使用2B铅笔,确定后必须使用黑色字迹的签字笔或钢笔描黑。
二、填空题:本题共7小题,其中11-14题每小题6分,15-17题每小题4分,共36分.
11.南宋时期,数学家秦九韶提出利用三角形的三边求面积的公式:如果一个三角形的三边长分别为,那么三角形的面积,后人称之为秦九韶公式.这与古希腊数学家海伦证明的面积公式,
实质是相同的.若在中,,,,则的面积为 ▲ , 的内切圆半径为 ▲ .
12.设变量,满足约束条件,则函数的最大值为 ▲ ,最小值为 ▲ .
13. 已知函数,则 ▲ ;若,则 ▲ .
14. 已知等差数列的首项,公差,且,,成等比数列,则 ▲ .若数列的通项,则的前项和 ▲ .
15.为了测量河对岸两点间的距离,现在沿岸相距的两点处分别测得,
假设四点在同一平面内,
则间的距离为 ▲ .
16. 已知椭圆,过右焦点且斜率为的直线与椭圆相交
于,两点,若,则椭圆的离心率为 ▲ .
17.已知正数满足,则的最大值为 ▲ .
三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)已知函数.
(Ⅰ)求;
(Ⅱ)求在上的值域.
19.(本题满分15分)在四棱锥中,平面平面,底面为直角梯形,,,分别为的中点.
(Ⅰ)证明://平面;
(Ⅱ)求与平面所成角的正弦值.
20.(本题满分15分)已知正项数列的前项的和为,且,
,数列的首项,且满足.
(Ⅰ)求数列,的通项公式;
(Ⅱ)设数列满足,求证:数列的前项和.
21.(本题满分15分)已知抛物线与椭圆有公共焦点,并交于两点.不与轴垂直的直线交抛物线于两点,且的中点在椭圆上,的垂直平分线交轴于点.
(Ⅰ)求抛物线的方程;
(Ⅱ)求点横坐标的取值范围.
22.(本题满分15分)已知函数,,
设.
(Ⅰ)若,且当时,求的最大值;
(Ⅱ)若存在实数,对任意的实数,使得方程恒有四个不同的实数解,求的最小值.
丽水市2020学年第二学期普通高中期末教学质量监控
高二 数学答案
一、选择题:BDDCB;BAACA;
二、填空题:
11.,. 12.,. 13. ,. 14. ,
15.. 16. 17..
18.(本题满分14分)
解:(Ⅰ)
(Ⅱ)
,
所以所求的值域为.
19.(本题满分15分)
(Ⅰ)证明:取AD中点,连接
平面,平面
平面,
平面,平面
平面,
平面平面
平面
(Ⅱ)平面平面
平面平面
平面
平面
以为原点, ,,分别为建立坐标系,设=1.
则,, ,,
,
,,
,
,
是平面的一个法向量,
设与平面所成的角为,
则
20解:(1) 当时,,解得
当时,,
两式相减得:,
又,所以,且
所以
由得
所以
(2)
两式相减得:
所以
所以
21.(本题满分15分)
解: (1)由已知得抛物线的焦点为(1,0),
所以,抛物线方程为
(2)设
两式相减得:
即
所以
即,
由题意得 化得,即
22.解:(1)当时,,
当时,递增,
当时,递减,
所以,当时,.
(a)当时,,为二次方程,不合题意.
(b)当时,,
,
方程无解,不合题意.
(c)当时,,
方程有四个不同的解,等价于直线与的图象有四个不同的交点,
由得在时恒成立,
由得在时恒成立,
对称轴方程,
,,
所以只要
(不合),
综上:的最小值为2.
同课章节目录
