浙江省丽水市普通高中2020-2021学年高一下学期期末教学质量监控数学试题 Word版含答案
文档属性
| 名称 | 浙江省丽水市普通高中2020-2021学年高一下学期期末教学质量监控数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 829.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 10:04:51 | ||
图片预览




文档简介
丽水市2020学年第二学期普通高中期末教学质量监控
高一数学 试题卷 (2021.07)
本试题卷分选择题和非选择题两部分。全卷共6页,满分150分,考试时间120分钟。
注意事项:
1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题卷规定的位置上。
2.答题时,请按照答题卷上“注意事项”的要求,在答题卷相应的位置上规范作答,在本试题卷上的作答一律无效。
选择题部分(共60分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数的虚部为
A. B. C. D.
2.先后抛掷一枚质地均匀的硬币两次,得到一次正面向上和一次反面向上的概率为
A. B. C. D.
3.已知平面向量,,,下列结论中正确的是
A.若,则 B.若,则
C.若,,则 D.若,则
4.已知某19个数据的平均数为5,方差为2,现加入一个数5,此时这20个数据的平均数为,方差为,则
A., B.,
C., D.,
5.从装有2个红球、4个白球的袋子中任意摸出2个球,事件“至少有1个红球”,
事件“至多有1个白球”,则
A. B.
C. D.
6.若向量,,则在上的投影向量为
A. B. C. D.
7.新冠肺炎疫情的发生,我国的三大产业均受到不同程度的影响,其中第三产业中的各个行业都面临着很大的营收压力.2020年7月国家统计局发布了我国上半年国内经济数据,如图所示:图1为国内三大产业比重,图2为第三产业中各行业比重.
以下关于我国上半年经济数据的说法正确的是
A.第一产业的生产总值与第三产业中“租赁和商务服务业”的生产总值基本持平
B.第一产业的生产总值超过第三产业中“房地产业”的生产总值
C.若“住宿餐饮业”生产总值为7500亿元,则“金融业”生产总值为32500亿元
D.若“金融业”生产总值为41040亿元,则第二产业生产总值为166500亿元
8.已知的外接圆圆心为,且,,则
A. B. C. D.
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)
9.设,是两条不同的直线,,是不同的平面,则下列结论正确的是
A.若,,则
B.若,,,则
C.若,,,则
D.若,,,则
10.下列四个命题中,不正确的是
A.若复数z满足,则
B.若复数,满足,则
C.若复数(),则为纯虚数的充要条件是
D.若,则
11.已知某地区有小学生人,初中生人,高中生人,当地教育部门为了了解本地区中小学生的近视率,按小学生、初中生、高中生进行分层抽样,抽取一个容量为的样本,得到小学生,初中生,高中生的近视率分别为,,.下列说法中正确的有
A.从高中生中抽取了人
B.每名学生被抽到的概率为
C.估计该地区中小学生总体的平均近视率为
D.估计高中学生的近视人数约为
12.已知正方体的棱长为,点是 的中点,点是侧面 内的动点,且满足,下列选项正确的是
A.动点轨迹的长度是
B.三角形在正方体内运动形成几何体的体积是
C.直线与所成的角为,则的最小值是
D.存在某个位置,使得直线与平面所成的角为
非选择题部分(共90分)
三、填空题(本大题共6小题,每小题5分,共30分)
13.空气质量指数(AQI)是定量描述空气质量状况的无量纲指数,AQI的数值越大、级别和类别越高,说明空气污染状况越严重.当空气质量指数在时,空气质量指数级别为一级(优);当空气质量指数在时,空气质量指数级别为二级(良)……为了加强环境保护,治理空气污染,环境监测部门对我市2020年的空气质量进行调研,随机抽取了100天的空气质量指数(AQI),得下表:
空气质量指数
天数
依据上表,估计我市某一天的空气质量指数级别为一级(优)的概率是 ▲ .
14.已知复数,则 ▲ .
15.在锐角中,角的对边分别为,若,,则边的取值范围是 ▲ .
16.已知复数满足,则的最大值是 ▲ .
17.已知球的球面面积为,四面体的四个顶点均在球面上,且平面,,,则该四面体的体积的最大值是 ▲ .
18.已知平面向量,,满足,,,则的最大值
是 ▲ .
四、解答题(本大题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤)
19.某景区的平面图如图所示,其中,为两条公路,,为公路上的两个景点,测得km,km,为了拓展旅游业务,拟在景区内建一个观景台,为了获得最佳观景效果,要求对的视角.现需要从观景台到建造两条观光路线.
(Ⅰ)求两地间的直线距离;
(Ⅱ)求观光线路长的取值范围.
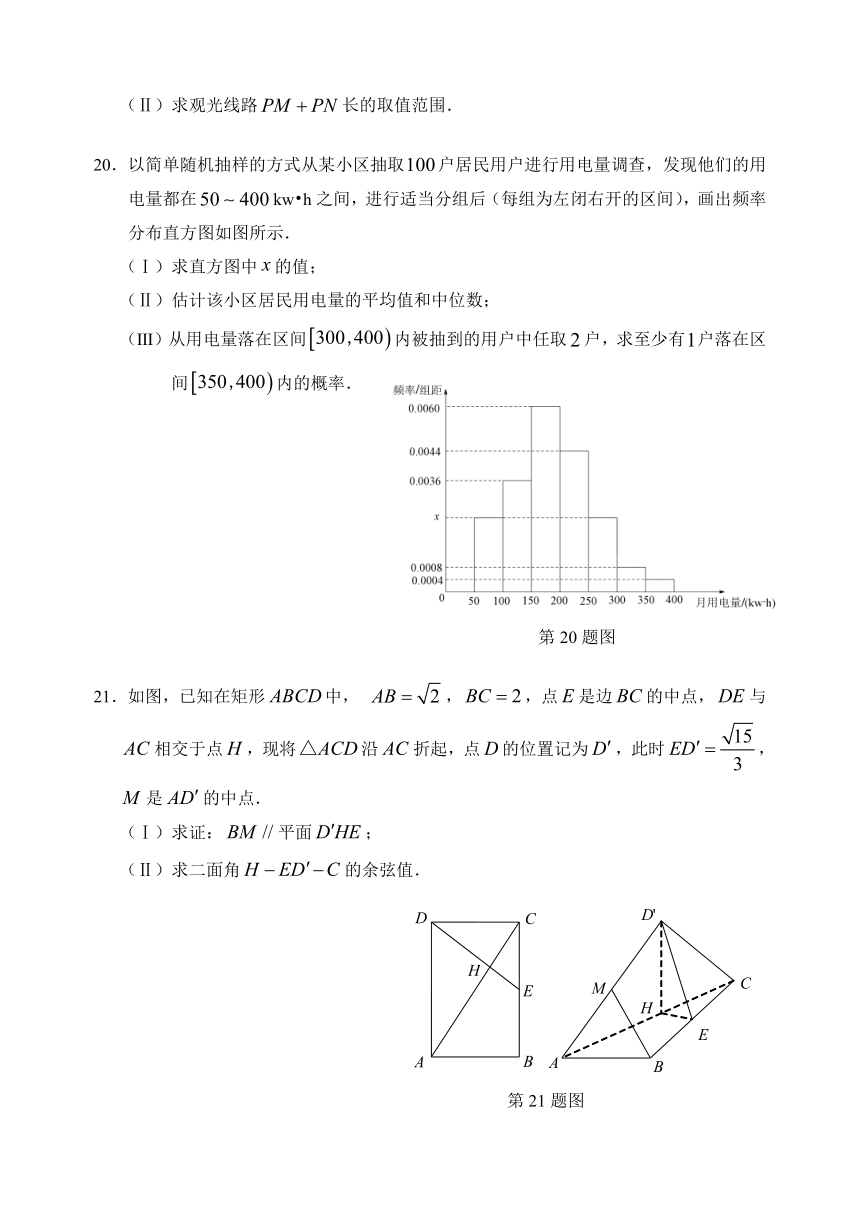
20.以简单随机抽样的方式从某小区抽取户居民用户进行用电量调查,发现他们的用电量都在kw?h之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示.
(Ⅰ)求直方图中的值;
(Ⅱ)估计该小区居民用电量的平均值和中位数;
(Ⅲ)从用电量落在区间内被抽到的用户中任取户,求至少有户落在区间内的概率.
21.如图,已知在矩形中, ,,点是边的中点,与相交于点,现将沿折起,点的位置记为,此时,是的中点.
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值.
22.在中,角的对边分别为.
(Ⅰ)已知,且 (在①,②,
③,这三个条件中任选两个补充到横线上),求;
(Ⅱ)若,,与交于点,过的直线分别交线段于两点,设,,求的最小值.
23.如图,已知在四棱锥中,底面是平行四边形,,
,,.
(Ⅰ)求与平面所成的角的正弦值;
(Ⅱ)棱上是否存在点,使得平面平面?若存在,求的值;若不存在,请说明理由.
丽水市2020学年第二学期普通高中期末教学质量监控
高一数学 答案 (2021.07)
一、单项选择题
CCDC BADA
多项选择题
9.BD 10.ACD 11.ABD 12.ABC
三、填空题
13. 14. 1 15.
16. 17. 18.
四、解答题
19.解:(Ⅰ)由余弦定理,得
.
所以两地间的直线距离为km …………6分
(Ⅱ)在中,设,
则…8分
所以
…………………10分
因为
所以
所以.………………12分
20.解:(Ⅰ)由
得……………3分
(Ⅱ)平均值
…………6分
因为用电量落在区间的频率之和为
所以中位数落在区,设中位数为,
则
解得,…………8分
(Ⅲ)易知用电量落在区间的用户有户,记为,用电量落在区间用户有2户,记为,记事件“至少有户落在区间内”.
则从,中这6个元素中任取2个元素的样本空间,,,,,,, ,,,,,,,,
,,,,, ,,,,
所以
即至少有户落在区间内的概率为.…12分
21.(Ⅰ)证明:取中点,连接,,
易得,
所以,
所以,平面
又因为,
所以平面
又,所以平面平面
所以平面…………6分
(Ⅱ)解:过点作于点,连结,易知,
所以,所以翻折后,,
所以平面,
所以,所以平面,
所以为二面角的平面角,
由,,,得,
所以,所以
所以
所以
即二面角的余弦值为.…………12分
22.解:(Ⅰ)由已知得
所以,
即,
所以,,所以.
若选①②
由,得,所以
由,得,
所以由,得
所以,
所以,得.
所以,.
若选②③
由,得,
又因为,
所以由正弦定理,得
所以,
若选①③
由,得,所以
又,所以
所以
所以…………6分
(Ⅱ)设,
则
因为三点共线,三点共线
所以,解得,
所以
由三点共线,得
所以
当且仅当,时,有最小值.……12分
23.解:(Ⅰ)取的中点,连结,过作于点,连,
又因为,所以为的外心,
又由,所以在平面上射影是的外心
所以平面,
所以平面平面,所以平面
所以为与平面所成的角
在中,,
所以,
与平面所成的角的正弦值.………6分
(Ⅱ)过作于点,连结,作交于点,交于点,
由(Ⅰ)得,所以平面,
所以
要使得平面平面,则需
在中,,,
所以,
于是.……………12分
高一数学 试题卷 (2021.07)
本试题卷分选择题和非选择题两部分。全卷共6页,满分150分,考试时间120分钟。
注意事项:
1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题卷规定的位置上。
2.答题时,请按照答题卷上“注意事项”的要求,在答题卷相应的位置上规范作答,在本试题卷上的作答一律无效。
选择题部分(共60分)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数的虚部为
A. B. C. D.
2.先后抛掷一枚质地均匀的硬币两次,得到一次正面向上和一次反面向上的概率为
A. B. C. D.
3.已知平面向量,,,下列结论中正确的是
A.若,则 B.若,则
C.若,,则 D.若,则
4.已知某19个数据的平均数为5,方差为2,现加入一个数5,此时这20个数据的平均数为,方差为,则
A., B.,
C., D.,
5.从装有2个红球、4个白球的袋子中任意摸出2个球,事件“至少有1个红球”,
事件“至多有1个白球”,则
A. B.
C. D.
6.若向量,,则在上的投影向量为
A. B. C. D.
7.新冠肺炎疫情的发生,我国的三大产业均受到不同程度的影响,其中第三产业中的各个行业都面临着很大的营收压力.2020年7月国家统计局发布了我国上半年国内经济数据,如图所示:图1为国内三大产业比重,图2为第三产业中各行业比重.
以下关于我国上半年经济数据的说法正确的是
A.第一产业的生产总值与第三产业中“租赁和商务服务业”的生产总值基本持平
B.第一产业的生产总值超过第三产业中“房地产业”的生产总值
C.若“住宿餐饮业”生产总值为7500亿元,则“金融业”生产总值为32500亿元
D.若“金融业”生产总值为41040亿元,则第二产业生产总值为166500亿元
8.已知的外接圆圆心为,且,,则
A. B. C. D.
二、多项选择题(本大题共4小题,每小题5分,共计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分)
9.设,是两条不同的直线,,是不同的平面,则下列结论正确的是
A.若,,则
B.若,,,则
C.若,,,则
D.若,,,则
10.下列四个命题中,不正确的是
A.若复数z满足,则
B.若复数,满足,则
C.若复数(),则为纯虚数的充要条件是
D.若,则
11.已知某地区有小学生人,初中生人,高中生人,当地教育部门为了了解本地区中小学生的近视率,按小学生、初中生、高中生进行分层抽样,抽取一个容量为的样本,得到小学生,初中生,高中生的近视率分别为,,.下列说法中正确的有
A.从高中生中抽取了人
B.每名学生被抽到的概率为
C.估计该地区中小学生总体的平均近视率为
D.估计高中学生的近视人数约为
12.已知正方体的棱长为,点是 的中点,点是侧面 内的动点,且满足,下列选项正确的是
A.动点轨迹的长度是
B.三角形在正方体内运动形成几何体的体积是
C.直线与所成的角为,则的最小值是
D.存在某个位置,使得直线与平面所成的角为
非选择题部分(共90分)
三、填空题(本大题共6小题,每小题5分,共30分)
13.空气质量指数(AQI)是定量描述空气质量状况的无量纲指数,AQI的数值越大、级别和类别越高,说明空气污染状况越严重.当空气质量指数在时,空气质量指数级别为一级(优);当空气质量指数在时,空气质量指数级别为二级(良)……为了加强环境保护,治理空气污染,环境监测部门对我市2020年的空气质量进行调研,随机抽取了100天的空气质量指数(AQI),得下表:
空气质量指数
天数
依据上表,估计我市某一天的空气质量指数级别为一级(优)的概率是 ▲ .
14.已知复数,则 ▲ .
15.在锐角中,角的对边分别为,若,,则边的取值范围是 ▲ .
16.已知复数满足,则的最大值是 ▲ .
17.已知球的球面面积为,四面体的四个顶点均在球面上,且平面,,,则该四面体的体积的最大值是 ▲ .
18.已知平面向量,,满足,,,则的最大值
是 ▲ .
四、解答题(本大题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤)
19.某景区的平面图如图所示,其中,为两条公路,,为公路上的两个景点,测得km,km,为了拓展旅游业务,拟在景区内建一个观景台,为了获得最佳观景效果,要求对的视角.现需要从观景台到建造两条观光路线.
(Ⅰ)求两地间的直线距离;
(Ⅱ)求观光线路长的取值范围.
20.以简单随机抽样的方式从某小区抽取户居民用户进行用电量调查,发现他们的用电量都在kw?h之间,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示.
(Ⅰ)求直方图中的值;
(Ⅱ)估计该小区居民用电量的平均值和中位数;
(Ⅲ)从用电量落在区间内被抽到的用户中任取户,求至少有户落在区间内的概率.
21.如图,已知在矩形中, ,,点是边的中点,与相交于点,现将沿折起,点的位置记为,此时,是的中点.
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值.
22.在中,角的对边分别为.
(Ⅰ)已知,且 (在①,②,
③,这三个条件中任选两个补充到横线上),求;
(Ⅱ)若,,与交于点,过的直线分别交线段于两点,设,,求的最小值.
23.如图,已知在四棱锥中,底面是平行四边形,,
,,.
(Ⅰ)求与平面所成的角的正弦值;
(Ⅱ)棱上是否存在点,使得平面平面?若存在,求的值;若不存在,请说明理由.
丽水市2020学年第二学期普通高中期末教学质量监控
高一数学 答案 (2021.07)
一、单项选择题
CCDC BADA
多项选择题
9.BD 10.ACD 11.ABD 12.ABC
三、填空题
13. 14. 1 15.
16. 17. 18.
四、解答题
19.解:(Ⅰ)由余弦定理,得
.
所以两地间的直线距离为km …………6分
(Ⅱ)在中,设,
则…8分
所以
…………………10分
因为
所以
所以.………………12分
20.解:(Ⅰ)由
得……………3分
(Ⅱ)平均值
…………6分
因为用电量落在区间的频率之和为
所以中位数落在区,设中位数为,
则
解得,…………8分
(Ⅲ)易知用电量落在区间的用户有户,记为,用电量落在区间用户有2户,记为,记事件“至少有户落在区间内”.
则从,中这6个元素中任取2个元素的样本空间,,,,,,, ,,,,,,,,
,,,,, ,,,,
所以
即至少有户落在区间内的概率为.…12分
21.(Ⅰ)证明:取中点,连接,,
易得,
所以,
所以,平面
又因为,
所以平面
又,所以平面平面
所以平面…………6分
(Ⅱ)解:过点作于点,连结,易知,
所以,所以翻折后,,
所以平面,
所以,所以平面,
所以为二面角的平面角,
由,,,得,
所以,所以
所以
所以
即二面角的余弦值为.…………12分
22.解:(Ⅰ)由已知得
所以,
即,
所以,,所以.
若选①②
由,得,所以
由,得,
所以由,得
所以,
所以,得.
所以,.
若选②③
由,得,
又因为,
所以由正弦定理,得
所以,
若选①③
由,得,所以
又,所以
所以
所以…………6分
(Ⅱ)设,
则
因为三点共线,三点共线
所以,解得,
所以
由三点共线,得
所以
当且仅当,时,有最小值.……12分
23.解:(Ⅰ)取的中点,连结,过作于点,连,
又因为,所以为的外心,
又由,所以在平面上射影是的外心
所以平面,
所以平面平面,所以平面
所以为与平面所成的角
在中,,
所以,
与平面所成的角的正弦值.………6分
(Ⅱ)过作于点,连结,作交于点,交于点,
由(Ⅰ)得,所以平面,
所以
要使得平面平面,则需
在中,,,
所以,
于是.……………12分
同课章节目录
