沪科版七年级上册数学 第3章 整合提升密码
文档属性
| 名称 | 沪科版七年级上册数学 第3章 整合提升密码 |  | |
| 格式 | doc | ||
| 文件大小 | 144.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 12:52:29 | ||
图片预览




文档简介
专训一:图表信息问题的四种类型
名师点金:二元一次方程组的应用是初中教材中的重要内容,也是中考的热点内容之一,特别是近几年中考中,将已知条件以图形或图表等形式给出,出题手法新颖,给人耳目一新的感觉.
实物信息类
1.如图,在东北大秧歌的踩高跷表演中,已知演员身高是高跷长度的2倍,高跷与腿重合部分的长度为28 cm,演员踩在高跷上时,头顶距离地面的高度为224 cm,设演员的身高为x cm,高跷的长度为y cm,求x,y的值.
(第1题)
表格信息类
2.(中考·连云港)小林在某商店购买商品A,B共三次,只有一次购买时,购买商品A,B同时打折,其余两次均按标价购买,三次购买商品A,B的数量和费用如下表:
购买商品A
的数量/个 购买商品B
的数量/个 购买总费
用/元
第一次购物 6 5 1 140
第二次购物 3 7 1 110
第三次购物 9 8 1 062
(1)小林以折扣价购买商品A,B是第________次购物;
(2)求出商品A,B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品的?
几何图形类
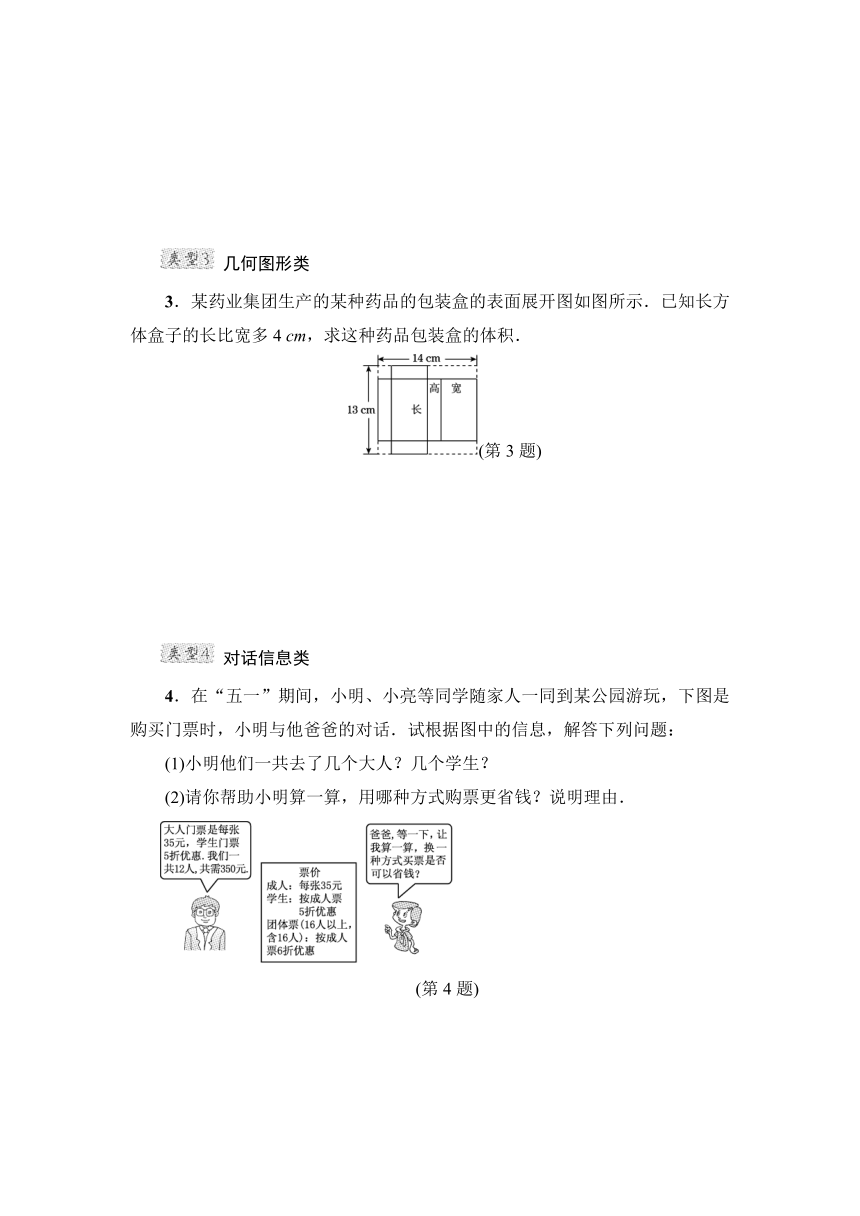
3.某药业集团生产的某种药品的包装盒的表面展开图如图所示.已知长方体盒子的长比宽多4 cm,求这种药品包装盒的体积.
(第3题)
对话信息类
4.在“五一”期间,小明、小亮等同学随家人一同到某公园游玩,下图是购买门票时,小明与他爸爸的对话.试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个大人?几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?说明理由.
(第4题)
专训二:巧用一次方程(组)选择方案
名师点金: 解方案选择题要仔细审题,弄清题目中条件之间的关系和作用;在选择合适的方案之前,应分析都有哪几种可行的方案,结合求出的每种方案的结果作出判断,培养把实际问题抽象为数学问题的能力和分析判断能力.
旅行社收费方案决策
1.张校长暑假将带领几名学生去北京旅游,甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠”;乙旅行社说:“包括校长在内全部按全票价的6折优惠”,全票价为240元.
(1)若学生有3人和5人,甲旅行社收费多少元?乙旅行社呢?
(2)学生有多少人时,两个旅行社的收费相同?
运输方式方案决策
2.某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时.其他主要参考数据如下:
运输工具 途中平均速
度(千米/时) 运费(元/千米) 装卸费用(元)
火车 100 15 2 000
汽车 80 20 900
(1)如果汽车的总支出费用比火车多1 100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与B市之间的路程为s千米,且知道火车与汽车在路上需临时停车耽误的时间分别为2小时和3.1小时.你若是A市水果批发部门的经理,要想将这批水果运往B市销售,你认为选择哪种运输方式比较合算?
购买方案决策
3.某商场计划拨款9万元从厂家购进50台电视机.已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1 500元,乙种每台2 100元,丙种每台2 500元.若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你帮助设计一下商场的进货方案.
上网计费方案决策
4.某地上网有两种收费方式,用户可任选其一:(A)计时制:2.8元/时;(B)包月制:60元/月.此外,每种收费方式都加收通信费1.2元/时.
(1)某用户每月上网20小时,选用哪种收费方式比较合算?
(2)某用户有120元钱用于上网(一个月),选用哪种收费方式比较合算?
(3)请你为用户设计一个方案,使用户能合理地选择收费方式.
专训三:几种常见的热门考点
名师点金:一元一次方程及方程组是初中数学的重点内容,也是中考的必考内容,其命题方向主要围绕方程(组)的相关概念、解法及应用几个方面.常见的题型有选择题、填空题、解答题,难度一般为中等.
一次方程(组)的相关概念
1.下列方程组是二元一次方程组的是( )
A. B.
C. D.
2.若关于x的方程ax+3=4x+1的解为正整数,则整数a 的值为( )
A.3或2 B.4 C.5 D.6
3.已知方程组的解为则2a-3b的值为( )
A.4 B.6 C.-6 D.-4
4.若关于x的方程(3-m)x2|m|-5+7=2是一元一次方程,则m=________.
等式的基本性质
5.下列等式变形正确的是( )
A.如果S=ab,那么b=
B.如果x=6,那么x=3
C.如果x-3=y-3,那么x-y=0
D.如果mx=my,那么x=y
6.已知x=y≠-,且xy≠0,下列各式:①x-3=y-3;②=;③=;④2x+2y=0,其中一定正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,标有相同字母的物体的质量相同,若A的质量为20克,当天平处于平衡状态时,B的质量为________克.
(第7题)
一次方程(组)的解法
8.下列方程组适合用代入法消元的是( )
A. B.
C. D.
9.解方程组时,为达到消元的目的,应该进行如下变形:①×________-②×________.
10.解下列方程:
(1)12-(3x-5)=7-5x;
(2)+=1.
11.解下列方程组:
(1) (2)
(3) (4)
一次方程(组)的应用
12.“六一”儿童节前夕,某超市用3 360元购进A、B两种童装共120套,其中A型童装每套24元,B型童装每套36元.设购买A型童装x套,B型童装y套,依题意列方程组正确的是( )
A. B.
C. D.
13.某种商品因换季准备打折出售.如果按定价的七五折出售将赔25元,而按定价的九折出售将赚20元,那么这种商品的定价是多少元?
14.为建设节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
小张家2015年4月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少.
思想方法
a.转化思想
15.二元一次方程x+y=7的非负整数解有( )
A.6个 B.7个 C.8个 D.无数个
b.整体思想
16.有甲、乙、丙三种商品,购买甲3件、乙2件、丙1件共需315元;购买甲1件、乙2件、丙3件共需285元,那么购买甲、乙、丙三种商品各一件共需________元.
c.数形结合思想
17.如图,数轴上两个动点A,B开始时所表示的数分别为-8,4,A,B两点各自以一定的速度在数轴上运动,且A点的运动速度为2个单位/秒.
(第17题)
(1)A,B两点同时出发相向而行,在原点处相遇,求B点的运动速度;
(2)A,B两点按上面的速度同时出发,向数轴正方向运动,几秒时两点相距6个单位?
(3)A,B两点按上面的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发向同方向运动,且在运动过程中,始终有CB∶CA=1∶2,若干秒后,C点在-10处,求此时B点的位置.
d.逆向思维法
18.李飒的妈妈买了几瓶饮料,第一天,他们全家喝了全部饮料的一半零半瓶;第二天,李飒招待来家中做客的同学,又喝了第一天剩下的饮料的一半零半瓶;第三天,李飒索性将第二天所剩的饮料的一半零半瓶喝了.这三天,正好把妈妈买的全部饮料喝光,则李飒的妈妈买的饮料一共有多少瓶?
答案
专训一
1.解:根据题意列方程组,得解得
故x的值为168,y的值为84.
2.解:(1)三
(2)设商品A,B的标价分别为x元、y元.
根据题意,得解得
答:商品A,B的标价分别为90元、120元.
(3)设商品A,B均打a折出售.
根据题意,得(9×90+8×120)×=1 062.
解得a=6.
答:商店是打6折出售这两种商品的.
3.解:方法一:设这种药品包装盒的高为x cm,则宽为 cm,长为(13-2x) cm.
依题意得13-2x-=4.
解得x=2.
方法二:设这种药品包装盒的宽为x cm,高为y cm,则长为(x+4) cm.
根据题意,得解得
故这种药品包装盒的长为9 cm,宽为5 cm,高为2 cm.
所以体积为9×5×2=90(cm3).
答:这种药品包装盒的体积为90 cm3.
4.解:(1)设一共去了x个大人,y个学生,
则解得
答:一共去了8个大人,4个学生.
(2)按团体票一次性购买16张门票更省钱.理由:
按团体票一次性购买16张门票需要35×60%×16=336(元),因为336<350,所以按团体票一次性购买更省钱.
专训二
1.解:(1)当有学生3人时,甲:240+240×0.5×3=600(元);
乙:(3+1)×240×0.6=576(元).
当有学生5人时,甲:240+240×0.5×5=840(元);
乙:(5+1)×240×0.6=864(元).
(2)设学生有x人.由题意,得
240+240×0.5x=(x+1)×240×0.6.解得x=4.
答:学生有4人时,两个旅行社的收费相同.
2.解:(1)设所求路程为x千米,则选择火车用的钱数为(+15x+2 000)元,选择汽车用的钱数为(+20x+900)元.
由题意,得+15x+2 000=+20x+900-1 100,解得x=400.
答:本市与A市之间的路程为400千米.
(2)选择火车用的钱数为×200+15s+2 000=17s+2 400(元),选择汽车用的钱数为×200+20s+900=22.5s+1 520(元).
当两种运输方式所用钱数相同时,即17s+2 400=22.5s+1 520,解得s=160.
所以当s等于160时,两种运输方式一样合算;当s小于160时,选择汽车运输比较合算;当s大于160时,选择火车运输比较合算.
3.解:设购进甲种电视机x台,乙种电视机y台,丙种电视机z台.
若购进甲、乙两种电视机,
列方程组为解得即购进甲种电视机25台,乙种电视机25台.
若购进甲、丙两种电视机,
列方程组为解得即购进甲种电视机35台,丙种电视机15台.
若购进乙、丙两种电视机,
列方程组为解得(不合题意,舍去)
综上所述,共有两种方案:一是购进甲种电视机25台,乙种电视机25台;二是购进甲种电视机35台,丙种电视机15台.
4.解:(1)计时制:20×(2.8+1.2)=80(元),
包月制:60+20×1.2=84(元).
因为80<84,所以选用计时制比较合算.
(2)120÷(2.8+1.2)=30(小时),
(120-60)÷1.2=50(小时).
因为30小时<50小时,所以选用包月制比较合算.
(3)设用户每月上网x小时,两种方式的费用一样.
由题意得:(2.8+1.2)x=60+1.2x,解得x=.
所以当用户每月上网时间大于小时时,选用包月制比较合算;
当用户每月上网时间小于小时时,选用计时制比较合算;
当用户每月上网时间等于小时时,选用计时制和包月制一样合算.
专训三
1.C 2.A 3.B 4.-3 5.C 6.B 7.10 8.B 9.3;2
10.解:(1)12-(3x-5)=7-5x,
12-3x+5= 7-5x,
2x= -10,
x= -5.
(2)+=1,
2(2x-5)+3(3-x)= 12,
4x-10+9-3x= 12,
x= 13.
11.解:(1)
将①代入②,得3x+(2x+5)=10,解得x=1.
将x=1代入①,得y=7.
所以原方程组的解为
(2)
①-②,得-2y=-4,解得y=2.
将y=2代入①,得3x-8=4,解得x=4.
所以原方程组的解为
(3)
整理原方程组得
③+②,得4x=32,解得x=8.
将x=8代入③,得8+2y=16,解得y=4.
所以原方程组的解为
(4)
①+②,得3x-3y=15,即x-y=5,④
②-③,得x+2y=11,⑤
联立④⑤组成方程组
解得将代入③,得7-2-z=7,解得z=-2.
所以原方程组的解为
12.B
13.解:设这种商品的定价是x元.
根据题意,得0.75x+25=0.9x-20,
解得x=300.
答:这种商品的定价是300元.
14.解:设“基本电价”为x元/千瓦时,“提高电价”为y元/千瓦时.
由题意得解得
答:“基本电价”为0.6元/千瓦时,“提高电价”为1元/千瓦时.
15.C 16.150
17.解:(1)设B点的运动速度为x个单位/秒,列方程为x=4.解得x=1.
答:B点的运动速度为1个单位/秒.
(2)设两点运动t秒时相距6个单位,
①当A点在B点的左侧时,
2t-t=(4+8)-6,解得t=6;
②当A点在B点的右侧时,
2t-t=(4+8)+6,解得t=18.
答:当A,B两点运动6秒或18秒时相距6个单位.
(3)设C点运动的速度为y个单位/秒,始终有CB∶CA=1∶2,则列方程得2-y=2(y-1).解得y=.当C点停留在-10处时,所用的时间为=(秒),
此时B点所表示的数为4-×1=-.
答:此时B点的位置是-所对应的点处.
点拨:本题利用数形结合思想,运用数轴辅助分析题意,找到相等关系,列方程得以求解.
18.解:设第三天李飒喝饮料之前,还有x瓶饮料,则+=x.解得x=1,
这也是第二天喝饮料之后所剩的饮料瓶数.
设第二天喝饮料之前还有y瓶饮料,则y-=1.解得y=3,这也是第一天喝饮料之后所剩的饮料瓶数.
再设第一天喝饮料之前有z瓶饮料,则z-=3.
解得z=7,这就是李飒的妈妈买的饮料的瓶数.
答:李飒的妈妈买的饮料一共有7瓶.
点拨:此题若按常规思维方法考虑非常困难,我们可利用逆向思维反向推理,问题便迎刃而解.
名师点金:二元一次方程组的应用是初中教材中的重要内容,也是中考的热点内容之一,特别是近几年中考中,将已知条件以图形或图表等形式给出,出题手法新颖,给人耳目一新的感觉.
实物信息类
1.如图,在东北大秧歌的踩高跷表演中,已知演员身高是高跷长度的2倍,高跷与腿重合部分的长度为28 cm,演员踩在高跷上时,头顶距离地面的高度为224 cm,设演员的身高为x cm,高跷的长度为y cm,求x,y的值.
(第1题)
表格信息类
2.(中考·连云港)小林在某商店购买商品A,B共三次,只有一次购买时,购买商品A,B同时打折,其余两次均按标价购买,三次购买商品A,B的数量和费用如下表:
购买商品A
的数量/个 购买商品B
的数量/个 购买总费
用/元
第一次购物 6 5 1 140
第二次购物 3 7 1 110
第三次购物 9 8 1 062
(1)小林以折扣价购买商品A,B是第________次购物;
(2)求出商品A,B的标价;
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品的?
几何图形类
3.某药业集团生产的某种药品的包装盒的表面展开图如图所示.已知长方体盒子的长比宽多4 cm,求这种药品包装盒的体积.
(第3题)
对话信息类
4.在“五一”期间,小明、小亮等同学随家人一同到某公园游玩,下图是购买门票时,小明与他爸爸的对话.试根据图中的信息,解答下列问题:
(1)小明他们一共去了几个大人?几个学生?
(2)请你帮助小明算一算,用哪种方式购票更省钱?说明理由.
(第4题)
专训二:巧用一次方程(组)选择方案
名师点金: 解方案选择题要仔细审题,弄清题目中条件之间的关系和作用;在选择合适的方案之前,应分析都有哪几种可行的方案,结合求出的每种方案的结果作出判断,培养把实际问题抽象为数学问题的能力和分析判断能力.
旅行社收费方案决策
1.张校长暑假将带领几名学生去北京旅游,甲旅行社说:“如果校长买全票一张,则其余学生可享受半价优惠”;乙旅行社说:“包括校长在内全部按全票价的6折优惠”,全票价为240元.
(1)若学生有3人和5人,甲旅行社收费多少元?乙旅行社呢?
(2)学生有多少人时,两个旅行社的收费相同?
运输方式方案决策
2.某市水果批发部门欲将A市的一批水果运往本市销售,有火车和汽车两种运输方式,运输过程中的损耗均为200元/时.其他主要参考数据如下:
运输工具 途中平均速
度(千米/时) 运费(元/千米) 装卸费用(元)
火车 100 15 2 000
汽车 80 20 900
(1)如果汽车的总支出费用比火车多1 100元,你知道本市与A市之间的路程是多少千米吗?请你列方程解答.
(2)如果A市与B市之间的路程为s千米,且知道火车与汽车在路上需临时停车耽误的时间分别为2小时和3.1小时.你若是A市水果批发部门的经理,要想将这批水果运往B市销售,你认为选择哪种运输方式比较合算?
购买方案决策
3.某商场计划拨款9万元从厂家购进50台电视机.已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1 500元,乙种每台2 100元,丙种每台2 500元.若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你帮助设计一下商场的进货方案.
上网计费方案决策
4.某地上网有两种收费方式,用户可任选其一:(A)计时制:2.8元/时;(B)包月制:60元/月.此外,每种收费方式都加收通信费1.2元/时.
(1)某用户每月上网20小时,选用哪种收费方式比较合算?
(2)某用户有120元钱用于上网(一个月),选用哪种收费方式比较合算?
(3)请你为用户设计一个方案,使用户能合理地选择收费方式.
专训三:几种常见的热门考点
名师点金:一元一次方程及方程组是初中数学的重点内容,也是中考的必考内容,其命题方向主要围绕方程(组)的相关概念、解法及应用几个方面.常见的题型有选择题、填空题、解答题,难度一般为中等.
一次方程(组)的相关概念
1.下列方程组是二元一次方程组的是( )
A. B.
C. D.
2.若关于x的方程ax+3=4x+1的解为正整数,则整数a 的值为( )
A.3或2 B.4 C.5 D.6
3.已知方程组的解为则2a-3b的值为( )
A.4 B.6 C.-6 D.-4
4.若关于x的方程(3-m)x2|m|-5+7=2是一元一次方程,则m=________.
等式的基本性质
5.下列等式变形正确的是( )
A.如果S=ab,那么b=
B.如果x=6,那么x=3
C.如果x-3=y-3,那么x-y=0
D.如果mx=my,那么x=y
6.已知x=y≠-,且xy≠0,下列各式:①x-3=y-3;②=;③=;④2x+2y=0,其中一定正确的有( )
A.1个 B.2个 C.3个 D.4个
7.如图,标有相同字母的物体的质量相同,若A的质量为20克,当天平处于平衡状态时,B的质量为________克.
(第7题)
一次方程(组)的解法
8.下列方程组适合用代入法消元的是( )
A. B.
C. D.
9.解方程组时,为达到消元的目的,应该进行如下变形:①×________-②×________.
10.解下列方程:
(1)12-(3x-5)=7-5x;
(2)+=1.
11.解下列方程组:
(1) (2)
(3) (4)
一次方程(组)的应用
12.“六一”儿童节前夕,某超市用3 360元购进A、B两种童装共120套,其中A型童装每套24元,B型童装每套36元.设购买A型童装x套,B型童装y套,依题意列方程组正确的是( )
A. B.
C. D.
13.某种商品因换季准备打折出售.如果按定价的七五折出售将赔25元,而按定价的九折出售将赚20元,那么这种商品的定价是多少元?
14.为建设节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
小张家2015年4月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少.
思想方法
a.转化思想
15.二元一次方程x+y=7的非负整数解有( )
A.6个 B.7个 C.8个 D.无数个
b.整体思想
16.有甲、乙、丙三种商品,购买甲3件、乙2件、丙1件共需315元;购买甲1件、乙2件、丙3件共需285元,那么购买甲、乙、丙三种商品各一件共需________元.
c.数形结合思想
17.如图,数轴上两个动点A,B开始时所表示的数分别为-8,4,A,B两点各自以一定的速度在数轴上运动,且A点的运动速度为2个单位/秒.
(第17题)
(1)A,B两点同时出发相向而行,在原点处相遇,求B点的运动速度;
(2)A,B两点按上面的速度同时出发,向数轴正方向运动,几秒时两点相距6个单位?
(3)A,B两点按上面的速度同时出发,向数轴负方向运动,与此同时,C点从原点出发向同方向运动,且在运动过程中,始终有CB∶CA=1∶2,若干秒后,C点在-10处,求此时B点的位置.
d.逆向思维法
18.李飒的妈妈买了几瓶饮料,第一天,他们全家喝了全部饮料的一半零半瓶;第二天,李飒招待来家中做客的同学,又喝了第一天剩下的饮料的一半零半瓶;第三天,李飒索性将第二天所剩的饮料的一半零半瓶喝了.这三天,正好把妈妈买的全部饮料喝光,则李飒的妈妈买的饮料一共有多少瓶?
答案
专训一
1.解:根据题意列方程组,得解得
故x的值为168,y的值为84.
2.解:(1)三
(2)设商品A,B的标价分别为x元、y元.
根据题意,得解得
答:商品A,B的标价分别为90元、120元.
(3)设商品A,B均打a折出售.
根据题意,得(9×90+8×120)×=1 062.
解得a=6.
答:商店是打6折出售这两种商品的.
3.解:方法一:设这种药品包装盒的高为x cm,则宽为 cm,长为(13-2x) cm.
依题意得13-2x-=4.
解得x=2.
方法二:设这种药品包装盒的宽为x cm,高为y cm,则长为(x+4) cm.
根据题意,得解得
故这种药品包装盒的长为9 cm,宽为5 cm,高为2 cm.
所以体积为9×5×2=90(cm3).
答:这种药品包装盒的体积为90 cm3.
4.解:(1)设一共去了x个大人,y个学生,
则解得
答:一共去了8个大人,4个学生.
(2)按团体票一次性购买16张门票更省钱.理由:
按团体票一次性购买16张门票需要35×60%×16=336(元),因为336<350,所以按团体票一次性购买更省钱.
专训二
1.解:(1)当有学生3人时,甲:240+240×0.5×3=600(元);
乙:(3+1)×240×0.6=576(元).
当有学生5人时,甲:240+240×0.5×5=840(元);
乙:(5+1)×240×0.6=864(元).
(2)设学生有x人.由题意,得
240+240×0.5x=(x+1)×240×0.6.解得x=4.
答:学生有4人时,两个旅行社的收费相同.
2.解:(1)设所求路程为x千米,则选择火车用的钱数为(+15x+2 000)元,选择汽车用的钱数为(+20x+900)元.
由题意,得+15x+2 000=+20x+900-1 100,解得x=400.
答:本市与A市之间的路程为400千米.
(2)选择火车用的钱数为×200+15s+2 000=17s+2 400(元),选择汽车用的钱数为×200+20s+900=22.5s+1 520(元).
当两种运输方式所用钱数相同时,即17s+2 400=22.5s+1 520,解得s=160.
所以当s等于160时,两种运输方式一样合算;当s小于160时,选择汽车运输比较合算;当s大于160时,选择火车运输比较合算.
3.解:设购进甲种电视机x台,乙种电视机y台,丙种电视机z台.
若购进甲、乙两种电视机,
列方程组为解得即购进甲种电视机25台,乙种电视机25台.
若购进甲、丙两种电视机,
列方程组为解得即购进甲种电视机35台,丙种电视机15台.
若购进乙、丙两种电视机,
列方程组为解得(不合题意,舍去)
综上所述,共有两种方案:一是购进甲种电视机25台,乙种电视机25台;二是购进甲种电视机35台,丙种电视机15台.
4.解:(1)计时制:20×(2.8+1.2)=80(元),
包月制:60+20×1.2=84(元).
因为80<84,所以选用计时制比较合算.
(2)120÷(2.8+1.2)=30(小时),
(120-60)÷1.2=50(小时).
因为30小时<50小时,所以选用包月制比较合算.
(3)设用户每月上网x小时,两种方式的费用一样.
由题意得:(2.8+1.2)x=60+1.2x,解得x=.
所以当用户每月上网时间大于小时时,选用包月制比较合算;
当用户每月上网时间小于小时时,选用计时制比较合算;
当用户每月上网时间等于小时时,选用计时制和包月制一样合算.
专训三
1.C 2.A 3.B 4.-3 5.C 6.B 7.10 8.B 9.3;2
10.解:(1)12-(3x-5)=7-5x,
12-3x+5= 7-5x,
2x= -10,
x= -5.
(2)+=1,
2(2x-5)+3(3-x)= 12,
4x-10+9-3x= 12,
x= 13.
11.解:(1)
将①代入②,得3x+(2x+5)=10,解得x=1.
将x=1代入①,得y=7.
所以原方程组的解为
(2)
①-②,得-2y=-4,解得y=2.
将y=2代入①,得3x-8=4,解得x=4.
所以原方程组的解为
(3)
整理原方程组得
③+②,得4x=32,解得x=8.
将x=8代入③,得8+2y=16,解得y=4.
所以原方程组的解为
(4)
①+②,得3x-3y=15,即x-y=5,④
②-③,得x+2y=11,⑤
联立④⑤组成方程组
解得将代入③,得7-2-z=7,解得z=-2.
所以原方程组的解为
12.B
13.解:设这种商品的定价是x元.
根据题意,得0.75x+25=0.9x-20,
解得x=300.
答:这种商品的定价是300元.
14.解:设“基本电价”为x元/千瓦时,“提高电价”为y元/千瓦时.
由题意得解得
答:“基本电价”为0.6元/千瓦时,“提高电价”为1元/千瓦时.
15.C 16.150
17.解:(1)设B点的运动速度为x个单位/秒,列方程为x=4.解得x=1.
答:B点的运动速度为1个单位/秒.
(2)设两点运动t秒时相距6个单位,
①当A点在B点的左侧时,
2t-t=(4+8)-6,解得t=6;
②当A点在B点的右侧时,
2t-t=(4+8)+6,解得t=18.
答:当A,B两点运动6秒或18秒时相距6个单位.
(3)设C点运动的速度为y个单位/秒,始终有CB∶CA=1∶2,则列方程得2-y=2(y-1).解得y=.当C点停留在-10处时,所用的时间为=(秒),
此时B点所表示的数为4-×1=-.
答:此时B点的位置是-所对应的点处.
点拨:本题利用数形结合思想,运用数轴辅助分析题意,找到相等关系,列方程得以求解.
18.解:设第三天李飒喝饮料之前,还有x瓶饮料,则+=x.解得x=1,
这也是第二天喝饮料之后所剩的饮料瓶数.
设第二天喝饮料之前还有y瓶饮料,则y-=1.解得y=3,这也是第一天喝饮料之后所剩的饮料瓶数.
再设第一天喝饮料之前有z瓶饮料,则z-=3.
解得z=7,这就是李飒的妈妈买的饮料的瓶数.
答:李飒的妈妈买的饮料一共有7瓶.
点拨:此题若按常规思维方法考虑非常困难,我们可利用逆向思维反向推理,问题便迎刃而解.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
