人教版五年级上册5 简易方程整理和复习课件(31张PPT)
文档属性
| 名称 | 人教版五年级上册5 简易方程整理和复习课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 14:19:54 | ||
图片预览










文档简介
(共31张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
整理和复习
简易方程
5
小组交流:本单元主要学习了哪些内容?
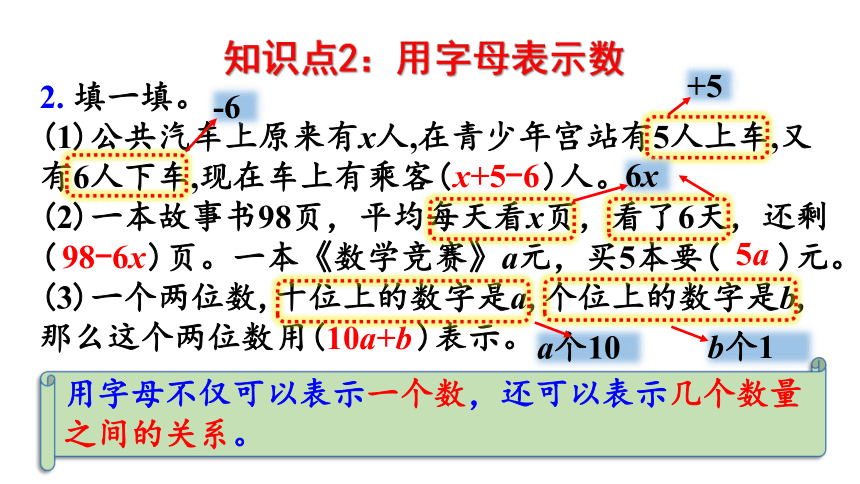
知识梳理
用字母表示数
解简易
方程
等式的性质
用字母表示运算定律及计算公式
借助字母解决实际问题并代入求值
方程的意义
解方程
用字母表示数量关系
简易方程
用方程解决实际问题
要点回顾
知识点1:用字母表示运算定律和计算公式
1. 填一填,说一说。
用字母可以表示我们学过的运算定律、运算性质、计算公式以及常用的数量关系。
(12.5+x)+8=12.5+( + )
4.5×a+6.5×a=a×( )
25-x-y=25 -( + )
s=v×( )
S平行四边形=a×( )
8
4.5+6.5
x
y
t
加法结合律
乘法分配律
x
连减的性质
速度、时间和路程的关系
h
平行四边形面积公式
知识点2:用字母表示数
2. 填一填。
(1)公共汽车上原来有x人,在青少年宫站有5人上车,又有6人下车,现在车上有乘客( )人。
(2)一本故事书98页,平均每天看x页,看了6天,还剩( )页。一本《数学竞赛》a元,买5本要( )元。
(3)一个两位数,十位上的数字是a,个位上的数字是b,那么这个两位数用( )表示。
x+5-6
98-6x
5a
10a+b
+5
-6
6x
a个10
b个1
用字母不仅可以表示一个数,还可以表示几个数量之间的关系。
知识点3:求含有字母式子的值
3. 小华家12月底用电抄表读数是2231千瓦时,11月底用电抄表读数是m千瓦时。小华家12月份应缴电费a元,(1)用含有字母的式子表示当地电费单价;
(2)当m=2130,a=56.56时,电费每千瓦时是多少元
(1) a÷(2231-m)
(2)当m=2130, a=56.56时,
a÷(2231-m)=56.56÷(2231-2130)=0.56(元/千瓦时)
水费÷(12月底读数- 11月底读数) =单价
把数值代入含有字母式子进行计算,结果注意不要忘了单位。
知识点4:含有字母式子的化简计算
4. 省略乘号并化简下列各式。
2×x = t×47 = a×4 = x×y =
9×y+5×y = a+a+6 =
12×x-7×x = 2.5×c-c =
2x
47t
4a
xy
14y
2a+6
5x
1.5c
在用字母表示的式子里,乘号可以用“·”代替,或省略不写;利用乘法的分配律还可以对一些较复杂的式子进行化简。
知识点5:方程的意义
5. 在方程后面画√。
6x+8 = 23 ( ) 8x-5 = 15×5 ( )
30a+5b ( ) 7x-8<36 ( )
10x = y ( ) (2.4+a)÷2.4 = 5 ( )
1÷8 = 0.125 ( ) 6x+8 = 9x-13 ( )
√
√
√
√
√
含有未知数的等式叫方程。判断一个式子是不是方程有两个条件:①是否等式;②是否含有未知数。二者缺一不可。
知识点6:等式的性质
6. 根据等式的性质填空。
(1)如果a=b(a、b均不为0),a+8=b+( );3a=b×( )
(2)如果3x = x+100,那么2x =( )
8
3
100
等式的性质1 等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
知识点7:解方程
7. 解下列方程。
(教材第83页整理和复习第1题)
x+4.8 = 7.2 x-6.5 = 3.2
解:x+4.8-4.8 = 7.2-4.8
x = 2.4
解:x-6.5+6.5 = 3.2+6.5
x = 9.7
知识点7:解方程
x÷8 = 0.4 6x+18 = 48
解:x÷8×8 = 0.4×8
x = 3.2
解: 6x+18-18 = 48-18
6x = 30
6x÷6 = 30÷6
x = 5
7. 解下列方程。
解方程要灵活运用等式的性质1和性质2;对于较复杂的方程,要注意明确把哪个式子看作整体。
3(x+2.1)= 10.5 12x-9x = 8.7
解:3(x+2.1)÷3 = 10.5÷3
x+2.1 = 3.5
x+2.1-2.1 = 3.5-2.1
x = 1.4
解:3x = 8.7
3x÷3 = 8.7÷3
x = 2.9
知识点7:解方程
7. 解下列方程。
检验: 把 x = 2.9代入原方程,
方程左边 = 12×2.9-9×2.9
= 8.7=方程右边
所以,x = 2.9是原方程的解。
解方程要注意书写格式,更要养成认真检验的好习惯。
知识点8:列方程解决实际问题
(1)
8. 列方程解决实际问题。
哈,93kg!这两个月我坚持锻炼,体重减少了3kg。
两个月前,他的体重是多少千克?
从图中你知道哪些信息?
(教材第83页整理和复习第2题)
现在的体重
要求的问题
知识点8:列方程解决实际问题
(1)
8. 列方程解决实际问题。
哈,93kg!这两个月我坚持锻炼,体重减少了3kg。
两个月前,他的体重是多少千克?
(教材第83页整理和复习第2题)
体重减少了3kg
现在的体重比两个月前的体重减少了3kg
两个月前的体重-3=现在的体重
两个月前的体重-3=现在的体重
解:设两个月前他的体重为x kg。
x-3 = 93
x-3+3 = 93+3
x = 96
检验: (1)经检验,所列的方程正确;
(2)把x = 96,代入原方程,
左边= 96-3
= 93=右边
所以,x = 96是原方程的解。
答:两个月前他的体重是96kg。
(2)
这条街一共有多少盏路灯?
解:设这条街一共有x盏路灯。
5x=140
5x÷5=140÷5
x=28
可根据“每盏路灯的灯泡数×路灯盏数=灯泡总个数”来列方程。
每盏路灯要装5个灯泡。
这条街一共需要140个灯泡。
检验:把结果代入原题中,
5×28=140(个),与原题中的条件一致,说明结果是正确的。
答:这条街一共有28盏路灯。
(3)
这里有两个未知量,可根据倍数关系来假设,两者的差来列方程。
3.65m
我的高度是你的3.5倍。
列方程解决问题有哪些步骤?检验时需要注意什么?
倍数关系
两者的差
解:设小鹿的高度为x m。
3.5x-x = 3.65
2.5x = 3.65
2.5x÷2.5 = 3.65÷2.5
x = 1.46
长颈鹿:1.46+3.65=5.11(m)
检验:把结果代入原题中,
5.11-1.46=3.65(m),5.11÷1.46=3.5
与原题中的条件完全一致,说明结果是正确的。
答:长颈鹿和小鹿的高度分别是5.11m和1.46m。
长颈鹿身高-小鹿身高=3.65m
列方程解决实际问题的步骤
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,
列方程;
(3)解方程并检验作答。
用方程解决问题有哪些步骤?检验时要注意什么?
检验时要注意两点:
(1)检验所得结果是不是方程的解;
(2)检验所得结果是否符合实际问题的意义。
课堂练习
1. 判断下面各题的叙述是否正确。
(1)> 2a。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)5x+5=5(x+ 1 )。 ( )
(4)x=6是方程3x-6=12 的解。 ( )
×
×
√
√
方程、方程的解和解方程等概念要区分清楚;和2a的意义也不同,也要注意分清。
(教材第84页第1题)
解:设这头大象重x吨。
25x-1= 124
25x-1 +1= 124+1
25x = 125
x = 5
答:这头大象重5吨。
2. 地球上最大的动物是蓝鲸。一头蓝鲸重124吨,比一头大象体重的25倍少1吨。这头大象重多少吨
一头大象的体重×25-1=一头蓝鲸的体重
解: 设小船的载质量是x吨。
8x+1000 = 25000
8x+1000-1000 = 25000-1000
8x = 24000
x = 3000
答:小船的载质量是3000吨。
3. 2002年8月15日,浙江省第一艘自行制造的载质量达25000吨的巨轮“阿斯娜”号从造船基地下水,驶向大海。
哇!它的载质量比我们的8倍还多1000吨。
可根据“它的载质量比我们的8倍还多1000吨”来找等量关系。
(教材第84页第5题)
4. 一个足球多少钱?
学校买来40支钢笔和20个足球,一共花了1180元。
8.5元/支
40支钢笔的价钱+20个足球的价钱=一共花的1180元
解:设一个足球x元。
8.5×40+20x = 1180
340+20x = 1180
20x = 840
x = 42
答:一个足球42元。
5. 有10元面值的人民币和5元面值的人民币共15张,合计120元。10元面值的人民币有多少张
5元面值人民币的和+ 10元面值人民币的和=120
解:设10元面值的人民币有x张,则5元面值的人
民币有(15-x)张。
10 x +(15-x)×5 = 120
75+5x = 560
75+5x-75= 120-75
5x = 45
x = 9
15-x=15-9=6
答: 10元面值的人
民币有6张。
小明和小红在校门口分手,7 分钟后他们同时到家。小明平均每分钟走45m,小红平均每分钟走多少米?
6.
这个问题可以想象为两人是同时从家出发,相向而行,结果在校门口相遇。这样就变成一道相遇问题。
(教材第85页第8题)
小红家
小明家
560m
解:设小红平均每分钟走x米。
45×7+7x = 560
315+7x = 560
315+7x-315 = 560-315
7x = 245
x = 35
答:小红平均每分钟走35米。
小红走的路程+小明走的路程=总路程
(教材第85页第8题)
方法一
解:设小红平均每分钟走x米。
(45+x)×7 = 560
(45+x)×7÷7 = 560÷7
45+x = 80
45+x-45 = 80-45
x = 35
答:小红平均每分钟走35米。
小红和小明走的速度和×所用时间=总路程
方法二
7.
他们分别有多少颗玻璃球?
我的玻璃球 是你的2倍。
要是你给我3颗,我们俩就一样多了。
(教材第85页第9*题)
女孩
男孩
男孩的是女孩的2倍
3颗
3颗
两人一样多
多(3×2)颗
男孩原
有颗数
-3=
女孩原
有颗数
+3
男孩原
有颗数
-
女孩原
有颗数
3×2
=
解: 设女孩原有玻璃球x颗,男孩有2x颗。
2x-3 = x+3
2x-3+3 = x+3+3
2x = x+6
2x-x = x+6-x
x = 6
6×2=12(颗)
答:女孩的玻璃球是6颗,男孩是12颗。
男孩原有颗数-3=女孩原有颗数+3
(教材第85页第9*题)
人教版数学
五年级上册
人教版数学五年级(上)
整理和复习
简易方程
5
小组交流:本单元主要学习了哪些内容?
知识梳理
用字母表示数
解简易
方程
等式的性质
用字母表示运算定律及计算公式
借助字母解决实际问题并代入求值
方程的意义
解方程
用字母表示数量关系
简易方程
用方程解决实际问题
要点回顾
知识点1:用字母表示运算定律和计算公式
1. 填一填,说一说。
用字母可以表示我们学过的运算定律、运算性质、计算公式以及常用的数量关系。
(12.5+x)+8=12.5+( + )
4.5×a+6.5×a=a×( )
25-x-y=25 -( + )
s=v×( )
S平行四边形=a×( )
8
4.5+6.5
x
y
t
加法结合律
乘法分配律
x
连减的性质
速度、时间和路程的关系
h
平行四边形面积公式
知识点2:用字母表示数
2. 填一填。
(1)公共汽车上原来有x人,在青少年宫站有5人上车,又有6人下车,现在车上有乘客( )人。
(2)一本故事书98页,平均每天看x页,看了6天,还剩( )页。一本《数学竞赛》a元,买5本要( )元。
(3)一个两位数,十位上的数字是a,个位上的数字是b,那么这个两位数用( )表示。
x+5-6
98-6x
5a
10a+b
+5
-6
6x
a个10
b个1
用字母不仅可以表示一个数,还可以表示几个数量之间的关系。
知识点3:求含有字母式子的值
3. 小华家12月底用电抄表读数是2231千瓦时,11月底用电抄表读数是m千瓦时。小华家12月份应缴电费a元,(1)用含有字母的式子表示当地电费单价;
(2)当m=2130,a=56.56时,电费每千瓦时是多少元
(1) a÷(2231-m)
(2)当m=2130, a=56.56时,
a÷(2231-m)=56.56÷(2231-2130)=0.56(元/千瓦时)
水费÷(12月底读数- 11月底读数) =单价
把数值代入含有字母式子进行计算,结果注意不要忘了单位。
知识点4:含有字母式子的化简计算
4. 省略乘号并化简下列各式。
2×x = t×47 = a×4 = x×y =
9×y+5×y = a+a+6 =
12×x-7×x = 2.5×c-c =
2x
47t
4a
xy
14y
2a+6
5x
1.5c
在用字母表示的式子里,乘号可以用“·”代替,或省略不写;利用乘法的分配律还可以对一些较复杂的式子进行化简。
知识点5:方程的意义
5. 在方程后面画√。
6x+8 = 23 ( ) 8x-5 = 15×5 ( )
30a+5b ( ) 7x-8<36 ( )
10x = y ( ) (2.4+a)÷2.4 = 5 ( )
1÷8 = 0.125 ( ) 6x+8 = 9x-13 ( )
√
√
√
√
√
含有未知数的等式叫方程。判断一个式子是不是方程有两个条件:①是否等式;②是否含有未知数。二者缺一不可。
知识点6:等式的性质
6. 根据等式的性质填空。
(1)如果a=b(a、b均不为0),a+8=b+( );3a=b×( )
(2)如果3x = x+100,那么2x =( )
8
3
100
等式的性质1 等式两边加上或减去同一个数,左右两边仍然相等。
等式的性质2 等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
知识点7:解方程
7. 解下列方程。
(教材第83页整理和复习第1题)
x+4.8 = 7.2 x-6.5 = 3.2
解:x+4.8-4.8 = 7.2-4.8
x = 2.4
解:x-6.5+6.5 = 3.2+6.5
x = 9.7
知识点7:解方程
x÷8 = 0.4 6x+18 = 48
解:x÷8×8 = 0.4×8
x = 3.2
解: 6x+18-18 = 48-18
6x = 30
6x÷6 = 30÷6
x = 5
7. 解下列方程。
解方程要灵活运用等式的性质1和性质2;对于较复杂的方程,要注意明确把哪个式子看作整体。
3(x+2.1)= 10.5 12x-9x = 8.7
解:3(x+2.1)÷3 = 10.5÷3
x+2.1 = 3.5
x+2.1-2.1 = 3.5-2.1
x = 1.4
解:3x = 8.7
3x÷3 = 8.7÷3
x = 2.9
知识点7:解方程
7. 解下列方程。
检验: 把 x = 2.9代入原方程,
方程左边 = 12×2.9-9×2.9
= 8.7=方程右边
所以,x = 2.9是原方程的解。
解方程要注意书写格式,更要养成认真检验的好习惯。
知识点8:列方程解决实际问题
(1)
8. 列方程解决实际问题。
哈,93kg!这两个月我坚持锻炼,体重减少了3kg。
两个月前,他的体重是多少千克?
从图中你知道哪些信息?
(教材第83页整理和复习第2题)
现在的体重
要求的问题
知识点8:列方程解决实际问题
(1)
8. 列方程解决实际问题。
哈,93kg!这两个月我坚持锻炼,体重减少了3kg。
两个月前,他的体重是多少千克?
(教材第83页整理和复习第2题)
体重减少了3kg
现在的体重比两个月前的体重减少了3kg
两个月前的体重-3=现在的体重
两个月前的体重-3=现在的体重
解:设两个月前他的体重为x kg。
x-3 = 93
x-3+3 = 93+3
x = 96
检验: (1)经检验,所列的方程正确;
(2)把x = 96,代入原方程,
左边= 96-3
= 93=右边
所以,x = 96是原方程的解。
答:两个月前他的体重是96kg。
(2)
这条街一共有多少盏路灯?
解:设这条街一共有x盏路灯。
5x=140
5x÷5=140÷5
x=28
可根据“每盏路灯的灯泡数×路灯盏数=灯泡总个数”来列方程。
每盏路灯要装5个灯泡。
这条街一共需要140个灯泡。
检验:把结果代入原题中,
5×28=140(个),与原题中的条件一致,说明结果是正确的。
答:这条街一共有28盏路灯。
(3)
这里有两个未知量,可根据倍数关系来假设,两者的差来列方程。
3.65m
我的高度是你的3.5倍。
列方程解决问题有哪些步骤?检验时需要注意什么?
倍数关系
两者的差
解:设小鹿的高度为x m。
3.5x-x = 3.65
2.5x = 3.65
2.5x÷2.5 = 3.65÷2.5
x = 1.46
长颈鹿:1.46+3.65=5.11(m)
检验:把结果代入原题中,
5.11-1.46=3.65(m),5.11÷1.46=3.5
与原题中的条件完全一致,说明结果是正确的。
答:长颈鹿和小鹿的高度分别是5.11m和1.46m。
长颈鹿身高-小鹿身高=3.65m
列方程解决实际问题的步骤
(1)找出未知数,用字母x表示;
(2)分析实际问题中的数量关系,找出等量关系,
列方程;
(3)解方程并检验作答。
用方程解决问题有哪些步骤?检验时要注意什么?
检验时要注意两点:
(1)检验所得结果是不是方程的解;
(2)检验所得结果是否符合实际问题的意义。
课堂练习
1. 判断下面各题的叙述是否正确。
(1)> 2a。 ( )
(2)含有未知数的式子叫做方程。 ( )
(3)5x+5=5(x+ 1 )。 ( )
(4)x=6是方程3x-6=12 的解。 ( )
×
×
√
√
方程、方程的解和解方程等概念要区分清楚;和2a的意义也不同,也要注意分清。
(教材第84页第1题)
解:设这头大象重x吨。
25x-1= 124
25x-1 +1= 124+1
25x = 125
x = 5
答:这头大象重5吨。
2. 地球上最大的动物是蓝鲸。一头蓝鲸重124吨,比一头大象体重的25倍少1吨。这头大象重多少吨
一头大象的体重×25-1=一头蓝鲸的体重
解: 设小船的载质量是x吨。
8x+1000 = 25000
8x+1000-1000 = 25000-1000
8x = 24000
x = 3000
答:小船的载质量是3000吨。
3. 2002年8月15日,浙江省第一艘自行制造的载质量达25000吨的巨轮“阿斯娜”号从造船基地下水,驶向大海。
哇!它的载质量比我们的8倍还多1000吨。
可根据“它的载质量比我们的8倍还多1000吨”来找等量关系。
(教材第84页第5题)
4. 一个足球多少钱?
学校买来40支钢笔和20个足球,一共花了1180元。
8.5元/支
40支钢笔的价钱+20个足球的价钱=一共花的1180元
解:设一个足球x元。
8.5×40+20x = 1180
340+20x = 1180
20x = 840
x = 42
答:一个足球42元。
5. 有10元面值的人民币和5元面值的人民币共15张,合计120元。10元面值的人民币有多少张
5元面值人民币的和+ 10元面值人民币的和=120
解:设10元面值的人民币有x张,则5元面值的人
民币有(15-x)张。
10 x +(15-x)×5 = 120
75+5x = 560
75+5x-75= 120-75
5x = 45
x = 9
15-x=15-9=6
答: 10元面值的人
民币有6张。
小明和小红在校门口分手,7 分钟后他们同时到家。小明平均每分钟走45m,小红平均每分钟走多少米?
6.
这个问题可以想象为两人是同时从家出发,相向而行,结果在校门口相遇。这样就变成一道相遇问题。
(教材第85页第8题)
小红家
小明家
560m
解:设小红平均每分钟走x米。
45×7+7x = 560
315+7x = 560
315+7x-315 = 560-315
7x = 245
x = 35
答:小红平均每分钟走35米。
小红走的路程+小明走的路程=总路程
(教材第85页第8题)
方法一
解:设小红平均每分钟走x米。
(45+x)×7 = 560
(45+x)×7÷7 = 560÷7
45+x = 80
45+x-45 = 80-45
x = 35
答:小红平均每分钟走35米。
小红和小明走的速度和×所用时间=总路程
方法二
7.
他们分别有多少颗玻璃球?
我的玻璃球 是你的2倍。
要是你给我3颗,我们俩就一样多了。
(教材第85页第9*题)
女孩
男孩
男孩的是女孩的2倍
3颗
3颗
两人一样多
多(3×2)颗
男孩原
有颗数
-3=
女孩原
有颗数
+3
男孩原
有颗数
-
女孩原
有颗数
3×2
=
解: 设女孩原有玻璃球x颗,男孩有2x颗。
2x-3 = x+3
2x-3+3 = x+3+3
2x = x+6
2x-x = x+6-x
x = 6
6×2=12(颗)
答:女孩的玻璃球是6颗,男孩是12颗。
男孩原有颗数-3=女孩原有颗数+3
(教材第85页第9*题)
