人教版五年级上册数学 7 数学广角——植树问题练习二十四课件(29张PPT)
文档属性
| 名称 | 人教版五年级上册数学 7 数学广角——植树问题练习二十四课件(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 15:17:02 | ||
图片预览








文档简介
(共29张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
练习二十四
数学广角
7
重点回顾
有关植树问题,你学会了哪些内容?
植树问题分为路线是不封闭的和封闭的两种情况。
不封闭的:两端都栽,植树棵数=间隔数+1;
两端不栽,植树棵数=间隔数-1;
只栽一端,植树棵数=间隔数。
封闭图形的与只栽一端的相同,植树棵数=间隔数。
练习巩固
(教材第109页练习二十四)
1. 马路一边栽了 25 棵梧桐树。如果每两棵梧桐中间栽一棵银杏树,一共要栽多少棵银杏树?
25 - 1 = 24(棵)
答:一共要栽 24 棵银杏树。
把银杏树就当成两棵树之间的间隔,这样就可根据“植数棵树-1=间隔数” 来解答。
2. 5路公共汽车行驶路线全长12 km,相邻两站之间的路程都是1 km。一共设有多少个车站?
12÷1 = 12(个)
12+1 = 13(个)
答:一共设有13个车站。
假如一个车站就是一棵树,这也是植树问题。
3. 工人们正在架设电线杆,相邻两根的距离是200 m。 在总长 3000 m 的笔直路上,一共要架设多少根电线杆(两端都架设)?
把电线杆看作树,那么这道题也是植树问题。
3000÷200 = 15(个)
15+1 = 16(根)
答:一共要架设16根电线杆。
4. 园林工人沿一条笔直的公路一侧植树,每隔6 m种一棵,一共种了36棵。从第一棵到最后一棵的距离有多远?
间隔数:36-1 = 35(个)
总路长:35×6 = 210(米)
答:从第一棵到最后一棵的距离有210米。
间隔数=植数棵树-1,
总路长=植株间距×间隔数。
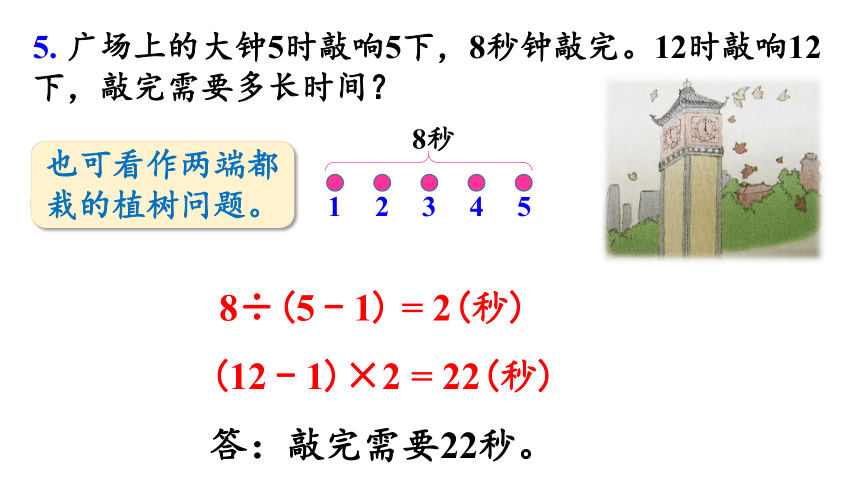
5. 广场上的大钟5时敲响5下,8秒钟敲完。12时敲响12下,敲完需要多长时间?
也可看作两端都栽的植树问题。
8÷(5 - 1) = 2(秒)
(12 - 1)×2 = 22(秒)
答:敲完需要22秒。
8秒
1
2
3
4
5
间隔数:32÷4 = 8(个)
植物盆数:8 - 1 = 7(盆)
答:一共要放 7 盆植物。
6. 一条走廊长 32 m,每隔 4 m 摆放一盆植物(两端不放)。一共要放多少盆植物?
把一盆植物看作树,就是植树问题。
服务点数=间隔数
把饮水服务点就当成树,就是一端栽,一端不栽的植树问题。
42÷3 = 14(处)
答:全程一共有 14 处这样的服务点。
7. 马拉松比赛全程约 42 km。平均每 3 km设置一处饮水服务点(起点不设,终点设),全程一共有多少处这样的服务点?
8. 一根木头长10 m,要把它平均分成5段。每锯下一段需要8分钟,锯完一共要花多少分钟?
锯1次
锯成2段
锯2次
锯成3段
锯3次
锯成4段
……
……
锯的次数=锯的段数-1
两端都不栽的植树问题
5 - 1 = 4(次)
8×4 = 32(分钟)
9. 笔直的跑道一旁插着51面小旗,它们的间隔是2m。现在要改为只插26面小旗(两端的旗子不动),间隔应改为多少米?
跑道的长度:
答:间隔应改为4米。
2×(51 1)=100(米)
间距:
100÷(26 1)=4(米)
两端都栽的植树问题。先要求出跑道的长,再求改动后的间距。
10. 解下列方程。
16+x = 71
解:
16+x-16 = 71 16
x = 55
3(2x 4)= 9
3(2x 4)÷3 = 9÷3
2x-4+4 = 3+4
2x÷2 = 7÷2
x = 3.5
解:
1.4x+9.2x = 53
10.6x = 53
10.6x÷10.6 = 53÷10.6
x = 5
解:
18+7x = 39
7x 18 = 39 18
7x÷7 = 21÷7
x = 3
解:
12.3x 7.5x = 57.6
4.8x = 57.6
4.8x÷4.8 = 57.6÷4.8
x = 12
(3x 7)÷5 = 16
(3x 7)÷5×5 = 16×5
3x-7+7 = 80+7
3x÷3 = 87÷3
x = 29
解:
解:
11. 一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样,10张桌子并成一排可以坐多少人?如果一共有38人,需要并多少张桌子才能坐下?
……
假设每两个人之间的间距为1,则有……
桌子数/张 长 宽 周长 间隔数/个 人数
1
2
3
…… … … …… …… ……
1×2=2
1
(2+1)×2=6
6÷1=6
6
2×2=4
1
(4+1)×2=10
10÷1=10
10
3×2=6
1
(6+1)×2=14
14÷1=14
14
10
10×2=20
1
(20+1)×2=42
42÷1=42
42
10张桌子并成一排可以坐多少人?
长方形的周长(因为间距为1,所以周长数=总间隔数)和围坐的人数之间存在着一一对应关系。
(10×2+1)×2=42(人)
10张桌子拼在一起的长
答:10张桌子并成一排可以坐42人。
解:
(2x+1)×2 = 38
x = 9
答:38人需要并9张桌子。
(2x+1)×2÷2 = 38÷2
2x+1-1 = 19 -1
2x ÷2 = 18÷2
如果一共有38人,需要并多少张桌子才能坐下?
设需要并x张桌子才能坐下。
60÷5=12(颗)
答:这条项链上共有12颗水晶。
12. 一条项链长60 cm,每隔5 cm有一颗水晶。这条项链上共有多少颗水晶?
把一颗颗水晶当成树,就可根据“植数棵树=间隔数”来解答。
13. 小区花园是一个长60 m,宽40 m的长方形。现在要在花园四周栽树,四个角上都要栽,每相邻两棵间隔5 m。一共要栽多少棵树?
封闭曲线上的植树问题:
长方形周长:(60+40)×2 = 200(m)
间隔数(植树棵数):200÷5 = 40(棵)
答:一共要栽40棵树。
14*. 围棋盘的最外层每边能放19枚棋子。最外层一共可以摆放多少棋子?
把棋子看作树,就是是封闭图形的植树问题:总棋子数=间隔数。
(19 1)×4=18×4=72(枚)
答:一共可以摆72枚棋子。
19×2+17×2=72(枚)
上下两边各有19枚棋子,左右两边各有17枚棋子。
……
……
……
……
19枚
17枚
这道题还有其他解题思路吗?
答:一共可以摆72枚棋子。
思路一
每边都只算1个顶点,每边各有18枚棋子。
……
……
……
……
18枚
(19 1)×4 =72(枚)
思路二
答:一共可以摆72枚棋子。
这道题还有其他解题思路吗?
4个顶点上的棋子先不算,每边各有17枚棋子。
……
……
……
……
17枚
17×4+4 =72(枚)
思路三
答:一共可以摆72枚棋子。
这道题还有其他解题思路吗?
15*. 为迎接“六一”儿童节, 学校举行团体操表演。五年级学生排成下面的方阵,最外层每边站15名学生, 最外层一共有多少名学生?整个方阵一共有多少名学生?
如果把最外层一圈看作正方形,把学生看作树,则这道题可以看作是封闭图形的植树问题。
15*. 为迎接“六一”儿童节, 学校举行团体操表演。五年级学生排成下面的方阵,最外层每边站15名学生, 最外层一共有多少名学生?整个方阵一共有多少名学生?
最外层:
(15 1)×4=56(名)
整个方阵:
15×15=225(名)
答:最外层一共有56名学生,
整个方阵一共有225名学生。
因为总人数=间隔数。每边站15名学生,有(15 1)个间隔,则4边一共……
在一条长150米的大路两边各栽一行树,起点和终点都栽,相邻两棵树之间的距离相等,一共栽了102棵,相邻两棵树之间的距离是多少米?
间隔数:102÷2-1=50(个)
间 距:150÷50=3(m)
答:相邻两棵树之间的距离是3米。
这是两端都栽的植树问题:
间隔数=植树棵数-1;
间距=总长÷间隔数。
每边的植树棵数=植树总数÷2
拓展提升
人教版数学
五年级上册
人教版数学五年级(上)
练习二十四
数学广角
7
重点回顾
有关植树问题,你学会了哪些内容?
植树问题分为路线是不封闭的和封闭的两种情况。
不封闭的:两端都栽,植树棵数=间隔数+1;
两端不栽,植树棵数=间隔数-1;
只栽一端,植树棵数=间隔数。
封闭图形的与只栽一端的相同,植树棵数=间隔数。
练习巩固
(教材第109页练习二十四)
1. 马路一边栽了 25 棵梧桐树。如果每两棵梧桐中间栽一棵银杏树,一共要栽多少棵银杏树?
25 - 1 = 24(棵)
答:一共要栽 24 棵银杏树。
把银杏树就当成两棵树之间的间隔,这样就可根据“植数棵树-1=间隔数” 来解答。
2. 5路公共汽车行驶路线全长12 km,相邻两站之间的路程都是1 km。一共设有多少个车站?
12÷1 = 12(个)
12+1 = 13(个)
答:一共设有13个车站。
假如一个车站就是一棵树,这也是植树问题。
3. 工人们正在架设电线杆,相邻两根的距离是200 m。 在总长 3000 m 的笔直路上,一共要架设多少根电线杆(两端都架设)?
把电线杆看作树,那么这道题也是植树问题。
3000÷200 = 15(个)
15+1 = 16(根)
答:一共要架设16根电线杆。
4. 园林工人沿一条笔直的公路一侧植树,每隔6 m种一棵,一共种了36棵。从第一棵到最后一棵的距离有多远?
间隔数:36-1 = 35(个)
总路长:35×6 = 210(米)
答:从第一棵到最后一棵的距离有210米。
间隔数=植数棵树-1,
总路长=植株间距×间隔数。
5. 广场上的大钟5时敲响5下,8秒钟敲完。12时敲响12下,敲完需要多长时间?
也可看作两端都栽的植树问题。
8÷(5 - 1) = 2(秒)
(12 - 1)×2 = 22(秒)
答:敲完需要22秒。
8秒
1
2
3
4
5
间隔数:32÷4 = 8(个)
植物盆数:8 - 1 = 7(盆)
答:一共要放 7 盆植物。
6. 一条走廊长 32 m,每隔 4 m 摆放一盆植物(两端不放)。一共要放多少盆植物?
把一盆植物看作树,就是植树问题。
服务点数=间隔数
把饮水服务点就当成树,就是一端栽,一端不栽的植树问题。
42÷3 = 14(处)
答:全程一共有 14 处这样的服务点。
7. 马拉松比赛全程约 42 km。平均每 3 km设置一处饮水服务点(起点不设,终点设),全程一共有多少处这样的服务点?
8. 一根木头长10 m,要把它平均分成5段。每锯下一段需要8分钟,锯完一共要花多少分钟?
锯1次
锯成2段
锯2次
锯成3段
锯3次
锯成4段
……
……
锯的次数=锯的段数-1
两端都不栽的植树问题
5 - 1 = 4(次)
8×4 = 32(分钟)
9. 笔直的跑道一旁插着51面小旗,它们的间隔是2m。现在要改为只插26面小旗(两端的旗子不动),间隔应改为多少米?
跑道的长度:
答:间隔应改为4米。
2×(51 1)=100(米)
间距:
100÷(26 1)=4(米)
两端都栽的植树问题。先要求出跑道的长,再求改动后的间距。
10. 解下列方程。
16+x = 71
解:
16+x-16 = 71 16
x = 55
3(2x 4)= 9
3(2x 4)÷3 = 9÷3
2x-4+4 = 3+4
2x÷2 = 7÷2
x = 3.5
解:
1.4x+9.2x = 53
10.6x = 53
10.6x÷10.6 = 53÷10.6
x = 5
解:
18+7x = 39
7x 18 = 39 18
7x÷7 = 21÷7
x = 3
解:
12.3x 7.5x = 57.6
4.8x = 57.6
4.8x÷4.8 = 57.6÷4.8
x = 12
(3x 7)÷5 = 16
(3x 7)÷5×5 = 16×5
3x-7+7 = 80+7
3x÷3 = 87÷3
x = 29
解:
解:
11. 一张桌子坐6人,两张桌子并起来坐10人,三张桌子并起来坐14人……照这样,10张桌子并成一排可以坐多少人?如果一共有38人,需要并多少张桌子才能坐下?
……
假设每两个人之间的间距为1,则有……
桌子数/张 长 宽 周长 间隔数/个 人数
1
2
3
…… … … …… …… ……
1×2=2
1
(2+1)×2=6
6÷1=6
6
2×2=4
1
(4+1)×2=10
10÷1=10
10
3×2=6
1
(6+1)×2=14
14÷1=14
14
10
10×2=20
1
(20+1)×2=42
42÷1=42
42
10张桌子并成一排可以坐多少人?
长方形的周长(因为间距为1,所以周长数=总间隔数)和围坐的人数之间存在着一一对应关系。
(10×2+1)×2=42(人)
10张桌子拼在一起的长
答:10张桌子并成一排可以坐42人。
解:
(2x+1)×2 = 38
x = 9
答:38人需要并9张桌子。
(2x+1)×2÷2 = 38÷2
2x+1-1 = 19 -1
2x ÷2 = 18÷2
如果一共有38人,需要并多少张桌子才能坐下?
设需要并x张桌子才能坐下。
60÷5=12(颗)
答:这条项链上共有12颗水晶。
12. 一条项链长60 cm,每隔5 cm有一颗水晶。这条项链上共有多少颗水晶?
把一颗颗水晶当成树,就可根据“植数棵树=间隔数”来解答。
13. 小区花园是一个长60 m,宽40 m的长方形。现在要在花园四周栽树,四个角上都要栽,每相邻两棵间隔5 m。一共要栽多少棵树?
封闭曲线上的植树问题:
长方形周长:(60+40)×2 = 200(m)
间隔数(植树棵数):200÷5 = 40(棵)
答:一共要栽40棵树。
14*. 围棋盘的最外层每边能放19枚棋子。最外层一共可以摆放多少棋子?
把棋子看作树,就是是封闭图形的植树问题:总棋子数=间隔数。
(19 1)×4=18×4=72(枚)
答:一共可以摆72枚棋子。
19×2+17×2=72(枚)
上下两边各有19枚棋子,左右两边各有17枚棋子。
……
……
……
……
19枚
17枚
这道题还有其他解题思路吗?
答:一共可以摆72枚棋子。
思路一
每边都只算1个顶点,每边各有18枚棋子。
……
……
……
……
18枚
(19 1)×4 =72(枚)
思路二
答:一共可以摆72枚棋子。
这道题还有其他解题思路吗?
4个顶点上的棋子先不算,每边各有17枚棋子。
……
……
……
……
17枚
17×4+4 =72(枚)
思路三
答:一共可以摆72枚棋子。
这道题还有其他解题思路吗?
15*. 为迎接“六一”儿童节, 学校举行团体操表演。五年级学生排成下面的方阵,最外层每边站15名学生, 最外层一共有多少名学生?整个方阵一共有多少名学生?
如果把最外层一圈看作正方形,把学生看作树,则这道题可以看作是封闭图形的植树问题。
15*. 为迎接“六一”儿童节, 学校举行团体操表演。五年级学生排成下面的方阵,最外层每边站15名学生, 最外层一共有多少名学生?整个方阵一共有多少名学生?
最外层:
(15 1)×4=56(名)
整个方阵:
15×15=225(名)
答:最外层一共有56名学生,
整个方阵一共有225名学生。
因为总人数=间隔数。每边站15名学生,有(15 1)个间隔,则4边一共……
在一条长150米的大路两边各栽一行树,起点和终点都栽,相邻两棵树之间的距离相等,一共栽了102棵,相邻两棵树之间的距离是多少米?
间隔数:102÷2-1=50(个)
间 距:150÷50=3(m)
答:相邻两棵树之间的距离是3米。
这是两端都栽的植树问题:
间隔数=植树棵数-1;
间距=总长÷间隔数。
每边的植树棵数=植树总数÷2
拓展提升
