人教版五年级上册数学8 总复习练习二十五课件(41张PPT)
文档属性
| 名称 | 人教版五年级上册数学8 总复习练习二十五课件(41张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 15:21:40 | ||
图片预览








文档简介
(共41张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
练习二十五
总复习
8
重点回顾
通过复习,你有哪些收获?
我学会了利用已经学过的知识解决新问题。
小数的乘除法都是转化为学过的整数除法来计算。
用字母表示未知数, 根据数量关系列方 程解决实际问题。
通过不断的学习,我发现数学在生活中的应用真多呀!
练习巩固
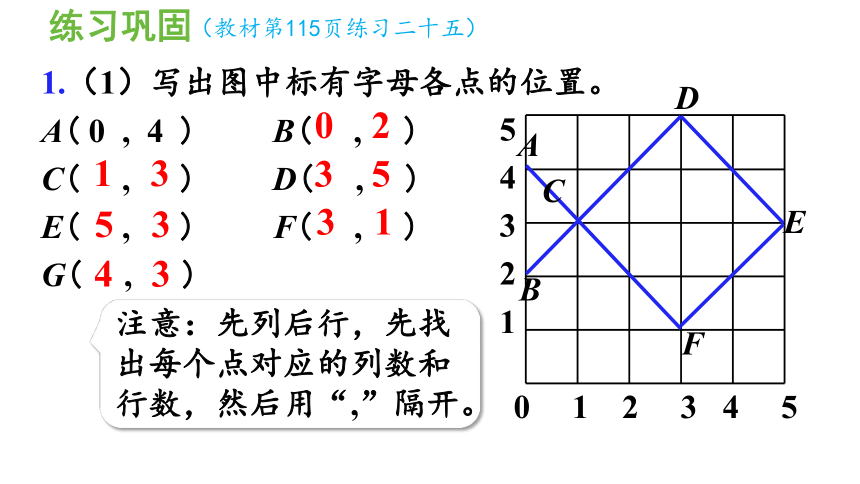
1.(1)写出图中标有字母各点的位置。
A( 0 , 4 ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , )
0 2
1 3
3 5
5 3
3 1
4 3
注意:先列后行,先找出每个点对应的列数和行数,然后用“,”隔开。
5
4
3
2
1
0 1 2 3 4 5
F
E
D
C
A
B
(教材第115页练习二十五)
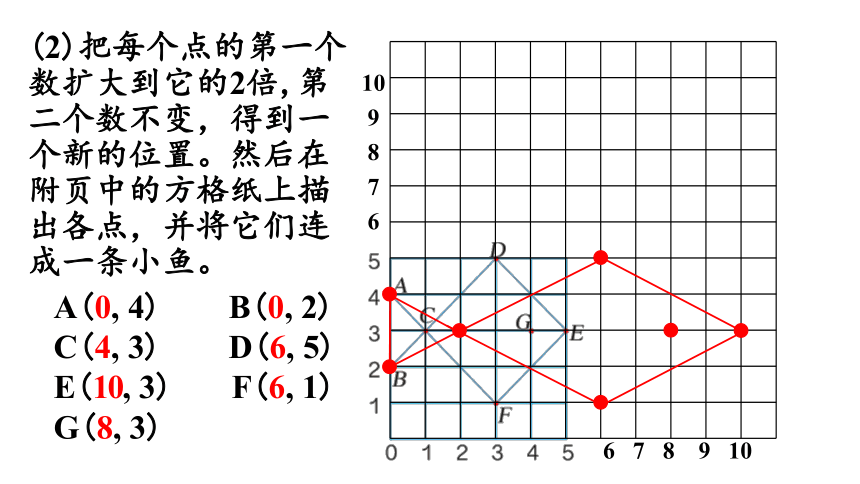
(2)把每个点的第一个数扩大到它的2倍,第二个数不变,得到一个新的位置。然后在附页中的方格纸上描出各点,并将它们连成一条小鱼。
10
9
8
7
6
6 7 8 9 10
A(0, 4) B(0, 2)
C(4, 3) D(6, 5)
E(10, 3) F(6, 1)
G(8, 3)
10
9
8
7
6
(3)每个点的第一个数不变,第二个数扩大到它的2倍。像上面那样,连成小鱼。
A(0, 8) B(0, 4)
C(2, 6) D(3, 10)
E(5, 6) F(3, 2)
G(4, 6)
6 7 8 9 10
10
9
8
7
6
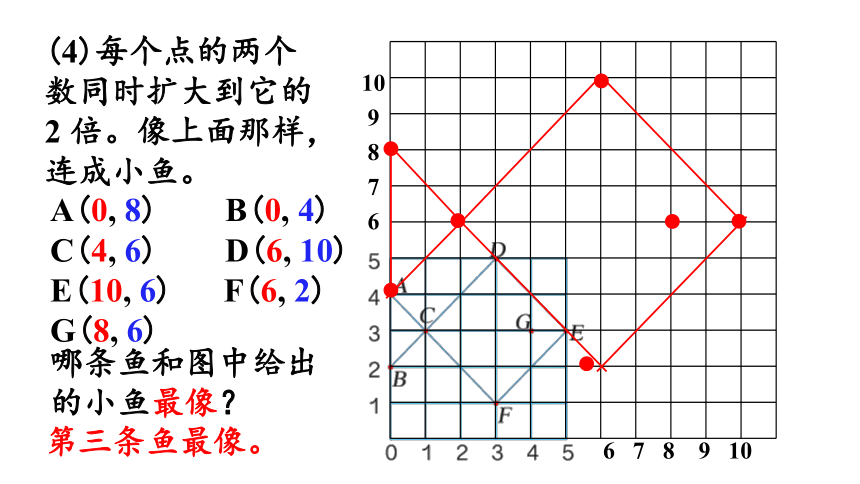
(4)每个点的两个数同时扩大到它的 2 倍。像上面那样,连成小鱼。
哪条鱼和图中给出
的小鱼最像?
第三条鱼最像。
A(0, 8) B(0, 4)
C(4, 6) D(6, 10)
E(10, 6) F(6, 2)
G(8, 6)
6 7 8 9 10
0 0 6 8 0
2.
计算下面各题。
32.5÷2.5=
1.36×0.05=
0.06×1.7=
13
0.068
0.102
2.5
3 2. 5
2 5
1
7 5
3
7 5
0
.
1. 3 6
× 0. 0 5
0 1 0 2
.
2
0.0 6
× 1.7
4
6
2.08×75=
156
1 5 6 0 0
.
0
2.0 8
× 7 5
4
6
1
0
5
4
1
65÷2.6=
25
2.6
6 5
5 2
2
1 3 0
5
1 3 0
0
0
2.3÷0.46=
5
0.46
2. 3
2 3 0
5
0
0
2.
计算下面各题。
3.根据我们学过的运算定律,在下面的□里填上合适的数,在○里填上合适的运算符号。
31.8× =1.2 ×
(2.5+3.5)× = × ○ ×4
(1.5×1.2)× =1.2×( ×4)
1.2
31.8
4
2.5
3.5
4
1.5
4
+
整数乘法的交换律、结合律和分配律对小数乘法同样适用。利用这些运算定律可以使一些计算简便。
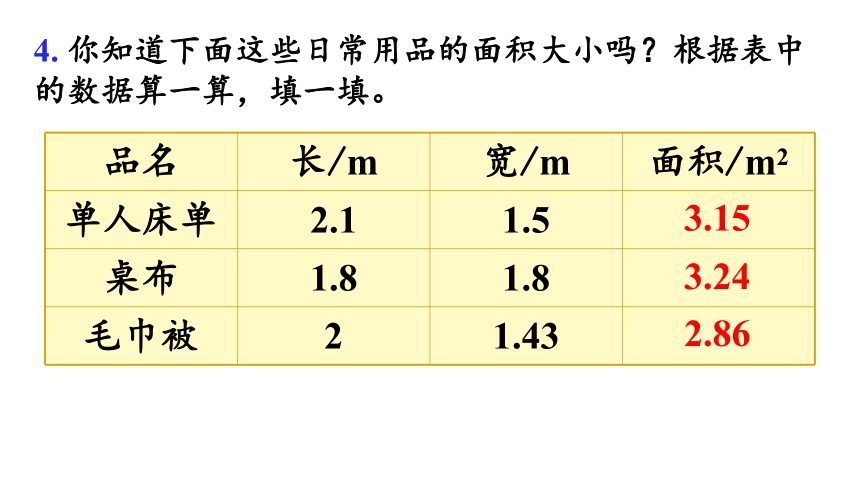
4. 你知道下面这些日常用品的面积大小吗?根据表中的数据算一算,填一填。
品名 长/m 宽/m 面积/m2
单人床单 2.1 1.5
桌布 1.8 1.8
毛巾被 2 1.43
3.15
3.24
2.86
5. 四川省峨眉山是我国降雨天数最多的地方。峨眉山的年降水量可达2033.9mm,平均每月降水量大约有多少毫米?(得数保留一位小数)
2033.9÷12 ≈ 169.5(mm)
答:平均每月降水量大约有169.5毫米。
根据“年降水量÷12=月降水量”列式。
按“四舍五入”法取近似数。
6.
解:设每箱饮料有x盒。
4x+4 = 52
4x+4-4 = 52-4
4x = 48
x = 12
答:每箱饮料有12盒。
我们班共52人,买4箱正好每人一盒。
每箱饮料有多少盒?
4整箱的盒数+送的盒数=总盒数
解:设每箱饮料有x盒。
4(x+1)= 52
4(x+1)÷4 = 52÷4
x+1 = 13
x = 12
答:每箱饮料有12盒。
每箱饮料有多少盒?
也可以这样列方程,你知道这两个方程有什么联系吗?
我们班共52人,买4箱正好每人一盒。
6.
(整箱的盒数+每箱送的盒
数) ×4=总盒数
7.一块街头广告牌的形状是平行四边形,底是12.5 m,高6.4 m。如果要油饰这块广告牌,每平方米用油漆0.6 kg,共需要多少千克油漆?
可根据平行四边形的面积公式先求出广告牌的面积。
再求需要多少千克的油漆。
7.一块街头广告牌的形状是平行四边形,底是12.5 m,高6.4 m。如果要油饰这块广告牌,每平方米用油漆0.6 kg,共需要多少千克油漆?
平行四边形的面积:
12.5×6.4=80(m2)
总共需要的油漆:
80×0.6=48(千克)
答:共需要48千克油漆。
8.一辆汽车的后车窗有一块遮阳布是梯形形状,上底是1m,下底是1.2m,高0.7m.它的面积是多少?
=(1+1.2)×0.7÷2
答:它的面积是0.77m2
= 0.77(m2)
S =
(a+b)h÷2
利用梯形面积公式求面积的时候,要注意书写格式,结果的单位名称也不要丢了。
1m
1.2m
0.7m
9. 一张边长4cm的正方形纸(下左图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是多少?
4×4-2×2÷2=14(cm2)
答:剩下的面积是14cm2 。
方法一
添补成正方形。
4×2+(2+4)×2÷2=14(cm2)
答:剩下的面积是14cm2 。
方法二
分割成长方形和梯形。
9. 一张边长4cm的正方形纸(下左图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是多少?
2×2÷2×7=14(cm2)
答:剩下的面积是14cm2 。
方法三
等分法。
9. 一张边长4cm的正方形纸(下左图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是多少?
把这个图形分成三个三角形和一个正方形。
10.你能想办法求出下图的面积吗?(小方格的边长为1cm.)
(7×2÷2)+(5×2÷2)+(5×5)+(5×1÷2)
= 39.5(cm2)
30+18÷2 = 39.5(cm2)
方法一
用数方格的方法求出它的面积。
方法二
指针停在哪种颜色区域的可能性最大?停在哪种颜色区域的可能性最小?
红色区域的可能性最大
黄色区域的可能性最小
蓝色区域的可能性最大
红色区域的可能性最小
11.
哪种颜色所占的面积大,指针停在哪种颜色区域的可能性就大。
序号 第一枚硬币 第二枚硬币 结果
1
2
3
4
12.
正
正
女孩赢
正
反
男孩赢
反
正
反
反
男孩赢
女孩赢
会有哪些可能的结果
如果两枚硬币朝上
的面相同,我获胜。
13.计算下面各题。
1.83+2.7=
2.73×1.5=
8
7
+
3
5
4
1
3
.
1
2
.
.
7
3
.
5
×
6
5
1
7
3
9
5
0
.
2
3
2
4
.
1
4.095
4.53
28.5÷15=
8.3 2.63=
5.67
1.9
1
.
15
5
3
2
8
5
5
9
3
5
0
1
.
1
1
3
6
7
6
5
0
3
.
8
2
.
.
13.计算下面各题。
5.5×
=5.5×
×
=5.5×24
=132
6.7
17.3
+
5.5
(17.3+6.7)
3.8+4.29+2.1+4.2
=(3.8+4.2)+(4.29+2.1)
=8+6.39
=14.39
3.8
4.2
8
13.计算下面各题。
14. 计算下面各题。(得数保留两位小数)
2
3
.
8
×
8
4
7
6
1
9
4
9
0
2
.
4
.
3
42.3×0.78 ≈
32.99
3
3
9
2
.
1.9
5
8
7
9
7
1
3
5
1
0
1
0
2
8
8
.
5
7
7
1
0
1
9
.
5.87÷1.9≈
3.09
11.9÷0.72≈
16.53
.
0.72
1
1
9
2
2
7
3
1
4
4
3
8
6
0
5
.
7
0
2
0
7
6
3
0
0
4
0
4
6
0
0
4
5
6
2
1
5
5
积的近似数,要先算出积再取值;
商的近似数,可以不用算出完全的商,只要除到比保留位数多一位即可。
15. 在下面的○里填上“>”或“<”。
9.9×6.9○70 0.97×23.8○24 57.5×6.2○420
15.6×2.1○30 26.4×1.08○26.4 5.9×7.8○48
<
<
<
<
>
>
我是先计算,再作比较。
我是先估算一下左边的积,利用估大法或估小法直接判定结果。
16. 从地球上向月球发射的一个激光信号,经过约2.56秒收到从月球反射回来的信号。已知光速是30万千米/秒,算一算这时月球到地球的距离是多少。
30×2.56÷2= 38.4(万千米)
答:这时月球到地球的距离是38.4万千米。
用激光测远距离既精确又迅速。
激光从地球到月球走了一个来回。
月球到地球的距离只是激光来回路程的一半。
17.解方程。
x÷1.44 =0.4
解:
x÷1.44×1.44 = 0.4×1.44
x=0.576
3.85+1.5x=6.1
3.85+1.5x 3.85 =6.1 3.85
1.5x÷1.5 =2.25÷1.5
x=1.5
解:
1.5x =2.25
6x 0.9=4.5
6x 0.9+0.9 =4.5+0.9
6x÷6 =5.4÷6
x=0.9
解:
6x =5.4
利用等式的性质1和性质2解方程时,要注意以下2点:
1.要注意格式;2.要养成认真检验的好习惯。
17.解方程。
18.一个玩具厂做一个毛绒兔原来需要3.8元的材料。后来改进了制作方法,每个只需3.6元的材料。原来准备做180个毛绒兔的材料,现在可以做多少个?
3.8×180=684(元)
原来180个毛绒兔的材料费:
改进制作方法后可以毛绒兔数量:
684÷3.6=190(个)
答:现在可以做190个。
19. 一条公路长360m,甲、乙两支施工队同时从公路的两端往中间铺柏油。甲队的施工速度是乙队的1.25倍,4天后这条公路全部铺完。甲、乙两队每天分别铺柏油路多少米
解:设乙队每天铺柏油路x m,则甲队每天铺柏油路1.25x m。
1.25x×4+4x = 360
9x = 360
x = 40
1.25×40 = 50(m)
答:甲、乙两队每天分别铺泊油路50 m,40 m。
还可以怎样列方程呢?
甲队铺的+乙队铺的=360
解:设乙队每天铺柏油路x m,则甲队每天铺柏油路1.25x m。
(1.25x+x)×4 = 360
9x = 360
x = 40
1.25×40 = 50(m)
答:甲、乙两队每天分别铺泊油路50 m,40 m。
这两个方程又有什么联系呢?
(甲队每天铺的+乙队每天铺的)×4=360
19. 一条公路长360m,甲、乙两支施工队同时从公路的两端往中间铺柏油。甲队的施工速度是乙队的1.25倍,4天后这条公路全部铺完。甲、乙两队每天分别铺柏油路多少米
20.王村有一个占地面积是3384m 的鱼塘(如下图)。村长告诉小林,鱼塘两条平行的边分别是84 m和60 m。小林用这学期的数学知识算出了这两条边的距离。
你能算出来吗?
上底和下底
?
两条边的距离就是梯形的高。
可根据梯形的面积公式求出这条高。
解:设这两条边的距离是x m。
(60+84)×x÷2 = 3384
x = 47
答:这两条边的距离是47 m。
144x÷2 = 3384
72x = 3384
72x÷72 = 3384÷72
21*.某地举行长跑比赛,运动员跑到离起点3km处要返回到起跑点。领先的运动员每分钟跑310 m,最后的运动员每分钟跑290 m。起跑后多少分钟这两个运动员相遇 相遇时离返回点有多少米
起跑点
返回点
两人共跑了2个3km
求出离返回点的距离。
根据“相遇时间=总路程÷两人的速度之和”即可求出相遇时间
21*.某地举行长跑比赛,运动员跑到离起点3km处要返回到起跑点。领先的运动员每分钟跑310 m,最后的运动员每分钟跑290 m。起跑后多少分钟这两个运动员相遇 相遇时离返回点有多少米
3km=3000m
(2×3000)÷(310+290)=10(分)
3000-290×10=100(m)
答:起跑后10分钟相遇。相遇时离返回点有100 m。
人教版数学
五年级上册
人教版数学五年级(上)
练习二十五
总复习
8
重点回顾
通过复习,你有哪些收获?
我学会了利用已经学过的知识解决新问题。
小数的乘除法都是转化为学过的整数除法来计算。
用字母表示未知数, 根据数量关系列方 程解决实际问题。
通过不断的学习,我发现数学在生活中的应用真多呀!
练习巩固
1.(1)写出图中标有字母各点的位置。
A( 0 , 4 ) B( , )
C( , ) D( , )
E( , ) F( , )
G( , )
0 2
1 3
3 5
5 3
3 1
4 3
注意:先列后行,先找出每个点对应的列数和行数,然后用“,”隔开。
5
4
3
2
1
0 1 2 3 4 5
F
E
D
C
A
B
(教材第115页练习二十五)
(2)把每个点的第一个数扩大到它的2倍,第二个数不变,得到一个新的位置。然后在附页中的方格纸上描出各点,并将它们连成一条小鱼。
10
9
8
7
6
6 7 8 9 10
A(0, 4) B(0, 2)
C(4, 3) D(6, 5)
E(10, 3) F(6, 1)
G(8, 3)
10
9
8
7
6
(3)每个点的第一个数不变,第二个数扩大到它的2倍。像上面那样,连成小鱼。
A(0, 8) B(0, 4)
C(2, 6) D(3, 10)
E(5, 6) F(3, 2)
G(4, 6)
6 7 8 9 10
10
9
8
7
6
(4)每个点的两个数同时扩大到它的 2 倍。像上面那样,连成小鱼。
哪条鱼和图中给出
的小鱼最像?
第三条鱼最像。
A(0, 8) B(0, 4)
C(4, 6) D(6, 10)
E(10, 6) F(6, 2)
G(8, 6)
6 7 8 9 10
0 0 6 8 0
2.
计算下面各题。
32.5÷2.5=
1.36×0.05=
0.06×1.7=
13
0.068
0.102
2.5
3 2. 5
2 5
1
7 5
3
7 5
0
.
1. 3 6
× 0. 0 5
0 1 0 2
.
2
0.0 6
× 1.7
4
6
2.08×75=
156
1 5 6 0 0
.
0
2.0 8
× 7 5
4
6
1
0
5
4
1
65÷2.6=
25
2.6
6 5
5 2
2
1 3 0
5
1 3 0
0
0
2.3÷0.46=
5
0.46
2. 3
2 3 0
5
0
0
2.
计算下面各题。
3.根据我们学过的运算定律,在下面的□里填上合适的数,在○里填上合适的运算符号。
31.8× =1.2 ×
(2.5+3.5)× = × ○ ×4
(1.5×1.2)× =1.2×( ×4)
1.2
31.8
4
2.5
3.5
4
1.5
4
+
整数乘法的交换律、结合律和分配律对小数乘法同样适用。利用这些运算定律可以使一些计算简便。
4. 你知道下面这些日常用品的面积大小吗?根据表中的数据算一算,填一填。
品名 长/m 宽/m 面积/m2
单人床单 2.1 1.5
桌布 1.8 1.8
毛巾被 2 1.43
3.15
3.24
2.86
5. 四川省峨眉山是我国降雨天数最多的地方。峨眉山的年降水量可达2033.9mm,平均每月降水量大约有多少毫米?(得数保留一位小数)
2033.9÷12 ≈ 169.5(mm)
答:平均每月降水量大约有169.5毫米。
根据“年降水量÷12=月降水量”列式。
按“四舍五入”法取近似数。
6.
解:设每箱饮料有x盒。
4x+4 = 52
4x+4-4 = 52-4
4x = 48
x = 12
答:每箱饮料有12盒。
我们班共52人,买4箱正好每人一盒。
每箱饮料有多少盒?
4整箱的盒数+送的盒数=总盒数
解:设每箱饮料有x盒。
4(x+1)= 52
4(x+1)÷4 = 52÷4
x+1 = 13
x = 12
答:每箱饮料有12盒。
每箱饮料有多少盒?
也可以这样列方程,你知道这两个方程有什么联系吗?
我们班共52人,买4箱正好每人一盒。
6.
(整箱的盒数+每箱送的盒
数) ×4=总盒数
7.一块街头广告牌的形状是平行四边形,底是12.5 m,高6.4 m。如果要油饰这块广告牌,每平方米用油漆0.6 kg,共需要多少千克油漆?
可根据平行四边形的面积公式先求出广告牌的面积。
再求需要多少千克的油漆。
7.一块街头广告牌的形状是平行四边形,底是12.5 m,高6.4 m。如果要油饰这块广告牌,每平方米用油漆0.6 kg,共需要多少千克油漆?
平行四边形的面积:
12.5×6.4=80(m2)
总共需要的油漆:
80×0.6=48(千克)
答:共需要48千克油漆。
8.一辆汽车的后车窗有一块遮阳布是梯形形状,上底是1m,下底是1.2m,高0.7m.它的面积是多少?
=(1+1.2)×0.7÷2
答:它的面积是0.77m2
= 0.77(m2)
S =
(a+b)h÷2
利用梯形面积公式求面积的时候,要注意书写格式,结果的单位名称也不要丢了。
1m
1.2m
0.7m
9. 一张边长4cm的正方形纸(下左图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是多少?
4×4-2×2÷2=14(cm2)
答:剩下的面积是14cm2 。
方法一
添补成正方形。
4×2+(2+4)×2÷2=14(cm2)
答:剩下的面积是14cm2 。
方法二
分割成长方形和梯形。
9. 一张边长4cm的正方形纸(下左图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是多少?
2×2÷2×7=14(cm2)
答:剩下的面积是14cm2 。
方法三
等分法。
9. 一张边长4cm的正方形纸(下左图),从相邻两边的中点连一条线段,沿这条线段剪去一个角,剩下的面积是多少?
把这个图形分成三个三角形和一个正方形。
10.你能想办法求出下图的面积吗?(小方格的边长为1cm.)
(7×2÷2)+(5×2÷2)+(5×5)+(5×1÷2)
= 39.5(cm2)
30+18÷2 = 39.5(cm2)
方法一
用数方格的方法求出它的面积。
方法二
指针停在哪种颜色区域的可能性最大?停在哪种颜色区域的可能性最小?
红色区域的可能性最大
黄色区域的可能性最小
蓝色区域的可能性最大
红色区域的可能性最小
11.
哪种颜色所占的面积大,指针停在哪种颜色区域的可能性就大。
序号 第一枚硬币 第二枚硬币 结果
1
2
3
4
12.
正
正
女孩赢
正
反
男孩赢
反
正
反
反
男孩赢
女孩赢
会有哪些可能的结果
如果两枚硬币朝上
的面相同,我获胜。
13.计算下面各题。
1.83+2.7=
2.73×1.5=
8
7
+
3
5
4
1
3
.
1
2
.
.
7
3
.
5
×
6
5
1
7
3
9
5
0
.
2
3
2
4
.
1
4.095
4.53
28.5÷15=
8.3 2.63=
5.67
1.9
1
.
15
5
3
2
8
5
5
9
3
5
0
1
.
1
1
3
6
7
6
5
0
3
.
8
2
.
.
13.计算下面各题。
5.5×
=5.5×
×
=5.5×24
=132
6.7
17.3
+
5.5
(17.3+6.7)
3.8+4.29+2.1+4.2
=(3.8+4.2)+(4.29+2.1)
=8+6.39
=14.39
3.8
4.2
8
13.计算下面各题。
14. 计算下面各题。(得数保留两位小数)
2
3
.
8
×
8
4
7
6
1
9
4
9
0
2
.
4
.
3
42.3×0.78 ≈
32.99
3
3
9
2
.
1.9
5
8
7
9
7
1
3
5
1
0
1
0
2
8
8
.
5
7
7
1
0
1
9
.
5.87÷1.9≈
3.09
11.9÷0.72≈
16.53
.
0.72
1
1
9
2
2
7
3
1
4
4
3
8
6
0
5
.
7
0
2
0
7
6
3
0
0
4
0
4
6
0
0
4
5
6
2
1
5
5
积的近似数,要先算出积再取值;
商的近似数,可以不用算出完全的商,只要除到比保留位数多一位即可。
15. 在下面的○里填上“>”或“<”。
9.9×6.9○70 0.97×23.8○24 57.5×6.2○420
15.6×2.1○30 26.4×1.08○26.4 5.9×7.8○48
<
<
<
<
>
>
我是先计算,再作比较。
我是先估算一下左边的积,利用估大法或估小法直接判定结果。
16. 从地球上向月球发射的一个激光信号,经过约2.56秒收到从月球反射回来的信号。已知光速是30万千米/秒,算一算这时月球到地球的距离是多少。
30×2.56÷2= 38.4(万千米)
答:这时月球到地球的距离是38.4万千米。
用激光测远距离既精确又迅速。
激光从地球到月球走了一个来回。
月球到地球的距离只是激光来回路程的一半。
17.解方程。
x÷1.44 =0.4
解:
x÷1.44×1.44 = 0.4×1.44
x=0.576
3.85+1.5x=6.1
3.85+1.5x 3.85 =6.1 3.85
1.5x÷1.5 =2.25÷1.5
x=1.5
解:
1.5x =2.25
6x 0.9=4.5
6x 0.9+0.9 =4.5+0.9
6x÷6 =5.4÷6
x=0.9
解:
6x =5.4
利用等式的性质1和性质2解方程时,要注意以下2点:
1.要注意格式;2.要养成认真检验的好习惯。
17.解方程。
18.一个玩具厂做一个毛绒兔原来需要3.8元的材料。后来改进了制作方法,每个只需3.6元的材料。原来准备做180个毛绒兔的材料,现在可以做多少个?
3.8×180=684(元)
原来180个毛绒兔的材料费:
改进制作方法后可以毛绒兔数量:
684÷3.6=190(个)
答:现在可以做190个。
19. 一条公路长360m,甲、乙两支施工队同时从公路的两端往中间铺柏油。甲队的施工速度是乙队的1.25倍,4天后这条公路全部铺完。甲、乙两队每天分别铺柏油路多少米
解:设乙队每天铺柏油路x m,则甲队每天铺柏油路1.25x m。
1.25x×4+4x = 360
9x = 360
x = 40
1.25×40 = 50(m)
答:甲、乙两队每天分别铺泊油路50 m,40 m。
还可以怎样列方程呢?
甲队铺的+乙队铺的=360
解:设乙队每天铺柏油路x m,则甲队每天铺柏油路1.25x m。
(1.25x+x)×4 = 360
9x = 360
x = 40
1.25×40 = 50(m)
答:甲、乙两队每天分别铺泊油路50 m,40 m。
这两个方程又有什么联系呢?
(甲队每天铺的+乙队每天铺的)×4=360
19. 一条公路长360m,甲、乙两支施工队同时从公路的两端往中间铺柏油。甲队的施工速度是乙队的1.25倍,4天后这条公路全部铺完。甲、乙两队每天分别铺柏油路多少米
20.王村有一个占地面积是3384m 的鱼塘(如下图)。村长告诉小林,鱼塘两条平行的边分别是84 m和60 m。小林用这学期的数学知识算出了这两条边的距离。
你能算出来吗?
上底和下底
?
两条边的距离就是梯形的高。
可根据梯形的面积公式求出这条高。
解:设这两条边的距离是x m。
(60+84)×x÷2 = 3384
x = 47
答:这两条边的距离是47 m。
144x÷2 = 3384
72x = 3384
72x÷72 = 3384÷72
21*.某地举行长跑比赛,运动员跑到离起点3km处要返回到起跑点。领先的运动员每分钟跑310 m,最后的运动员每分钟跑290 m。起跑后多少分钟这两个运动员相遇 相遇时离返回点有多少米
起跑点
返回点
两人共跑了2个3km
求出离返回点的距离。
根据“相遇时间=总路程÷两人的速度之和”即可求出相遇时间
21*.某地举行长跑比赛,运动员跑到离起点3km处要返回到起跑点。领先的运动员每分钟跑310 m,最后的运动员每分钟跑290 m。起跑后多少分钟这两个运动员相遇 相遇时离返回点有多少米
3km=3000m
(2×3000)÷(310+290)=10(分)
3000-290×10=100(m)
答:起跑后10分钟相遇。相遇时离返回点有100 m。
