鲁教版六年级上册数学第2章 2.7.1有理数的乘法习题课件 (26张PPT)
文档属性
| 名称 | 鲁教版六年级上册数学第2章 2.7.1有理数的乘法习题课件 (26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 393.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 09:01:17 | ||
图片预览








文档简介
有理数的乘法
鲁教版 六年级上
第二章 有理数及其运算
7
第1课时 有理数的乘法
A
C
1
2
3
4
5
D
D
6
7
8
A
答 案 呈 现
温馨提示:点击 进入讲评
习题链接
9
C
10
11
12
D
D
C
B
B
13
14
温馨提示:点击 进入讲评
习题链接
15
16
17
答 案 呈 现
A
18
A
1
【中考·安顺】计算(-3)×2的结果是( )
A.-6 B.-1
C.1 D.6
【天津二模】计算-4×(-2)的结果等于( )
A.12 B.-12
C.8 D.-8
2
C
3
D
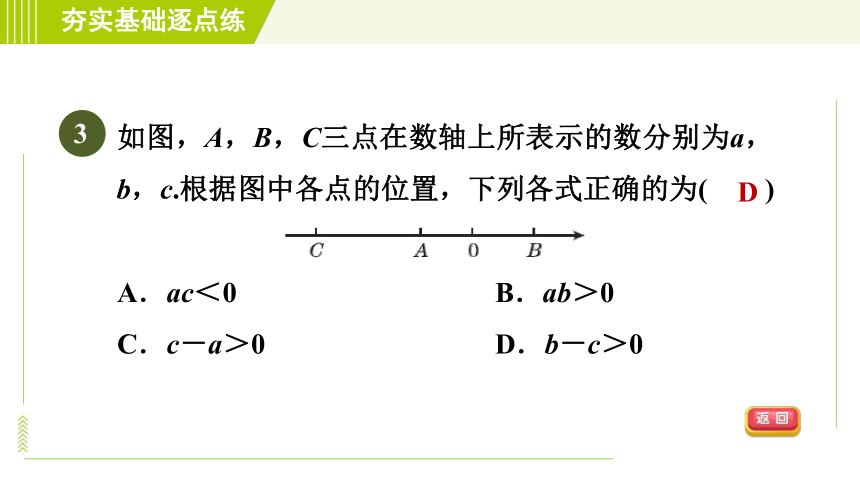
如图,A,B,C三点在数轴上所表示的数分别为a,b,c.根据图中各点的位置,下列各式正确的为( )
?
A.ac<0 B.ab>0
C.c-a>0 D.b-c>0
D
4
若ab>0,则a,b的符号最正确的表述是( )
A.a,b都为正 B.a,b都为负
C.a,b是一正一负 D.a,b是同号
【聊城东阿期末】如果a+b>0,且ab>0,那么( )
A.a>0,b>0
B.a<0,b<0
C.a,b异号且正数的绝对值较小
D.a,b异号且负数的绝对值较小
A
5
如图,数轴上的A,B两点所表示的数分别为a,b,且a+b<0,ab<0,则原点O的位置在( )
?
A.点A的右边
B.点B的左边
C.A,B两点之间,且靠近点A
D.A,B两点之间,且靠近点B
6
C
【点拨】因为数轴上的A,B两点所表示的数分别为a,b,且a+b<0,ab<0,所以a与b异号且b绝对值大,即a>0,b<0,|b|>|a|.所以原点O的位置在A,B两点之间,且靠近点A.
若|a|=3,|b|=4,且ab>0,则式子a+b的值是( )
A.7 B.1
C.1或-1 D.7 或-7
7
D
【点拨】因为|a|=3,|b|=4,所以a=±3,b=±4.
因为ab>0,所以当a=3时,b=4,则a+b=7,
当a=-3时,b=-4,则a+b=-7.
综上所述,a+b的值是7或-7.
8
解:(+4)×(-5)=-4×5=-20;
计算:
(1)(+4)×(-5);
(2)(-0.125)×(-8);
(4)0×(-13.52);
(6)(-1)×a.
(-0.125)×(-8)=0.125×8=1;
0×(-13.52)=0;
(-1)×a=-a.
9
D
10
C
若数a,b互为倒数,则( )
A.a-b=0 B.ab=1
C.a+b=0 D.ab=-1
11
B
下列叙述中错误的个数是( )
①任何有理数都有倒数
②互为倒数的两个数的积为1
③若a>0,b<0,则ab<0
④若a+b=0,则ab<0
A.1 B.2 C.3 D.4
12
B
【点拨】①任何非0的有理数都有倒数;②互为倒数的两个数的积为1;③若a>0,b<0,则ab<0;④若a+b=0,则ab≤0.故①④错误.
13
求下列各数的倒数.
14
下列说法中,正确的是( )
①两个正数中倒数大的反而小;
②两个负数中倒数大的反而小;
③两个有理数中倒数大的反而小;
④两个符号相同的有理数中倒数大的反而小.
A.①②④ B.① C.①②③ D.①④
A
错解:C
诊断:只要两个数同号,那么倒数大的反而小,未限定符号时,不能说哪个大.
正解:A
计算:
15
原式=4+1=5;
(3)4+(-0.5)×(-2);
(4)-3-0.125×8.
原式=-3-1=-4.
一辆出租车在一条东西走向的大街上行驶,这辆出租车连续送客20次,其中8次向东行驶,12次向西行驶,向东每次行驶10 km,向西每次行驶7 km.
16
(1)该出租车连续20次送客后,停在何处?
(2)该出租车一共行驶了多少千米的路程?
解:以向东为正方向,
则8×(+10)+12×(-7)=80-84=-4(km).
即该出租车停在出发点西边4 km处.
8×|+10|+12×|-7|=80+84=164(km).
故该出租车一共行驶了164 km的路程.
17
【点拨】本题运用分类讨论思想,x的绝对值是分
x=2和x=-2两种情况讨论.
解:因为a,b互为相反数,c,d互为倒数,x的绝对值是2.所以a+b=0,cd=1,x=2或x=-2.
18
规定一种新运算“*”,两数a,b通过“*”运算得(a+2)×2-b,即a*b=(a+2)×2-b,例如:3*5=(3+2)×2-5=10-5=5.根据上面的规定解答下题:
(1)求7*(-3)的值;
(2)7*(-3)与(-3)*7的值相等吗?
解:7*(-3)=(7+2)×2-(-3)=21.
因为(-3)*7=[(-3)+2]×2-7=-9,所以7*(-3)与(-3)*7的值不相等.
鲁教版 六年级上
第二章 有理数及其运算
7
第1课时 有理数的乘法
A
C
1
2
3
4
5
D
D
6
7
8
A
答 案 呈 现
温馨提示:点击 进入讲评
习题链接
9
C
10
11
12
D
D
C
B
B
13
14
温馨提示:点击 进入讲评
习题链接
15
16
17
答 案 呈 现
A
18
A
1
【中考·安顺】计算(-3)×2的结果是( )
A.-6 B.-1
C.1 D.6
【天津二模】计算-4×(-2)的结果等于( )
A.12 B.-12
C.8 D.-8
2
C
3
D
如图,A,B,C三点在数轴上所表示的数分别为a,b,c.根据图中各点的位置,下列各式正确的为( )
?
A.ac<0 B.ab>0
C.c-a>0 D.b-c>0
D
4
若ab>0,则a,b的符号最正确的表述是( )
A.a,b都为正 B.a,b都为负
C.a,b是一正一负 D.a,b是同号
【聊城东阿期末】如果a+b>0,且ab>0,那么( )
A.a>0,b>0
B.a<0,b<0
C.a,b异号且正数的绝对值较小
D.a,b异号且负数的绝对值较小
A
5
如图,数轴上的A,B两点所表示的数分别为a,b,且a+b<0,ab<0,则原点O的位置在( )
?
A.点A的右边
B.点B的左边
C.A,B两点之间,且靠近点A
D.A,B两点之间,且靠近点B
6
C
【点拨】因为数轴上的A,B两点所表示的数分别为a,b,且a+b<0,ab<0,所以a与b异号且b绝对值大,即a>0,b<0,|b|>|a|.所以原点O的位置在A,B两点之间,且靠近点A.
若|a|=3,|b|=4,且ab>0,则式子a+b的值是( )
A.7 B.1
C.1或-1 D.7 或-7
7
D
【点拨】因为|a|=3,|b|=4,所以a=±3,b=±4.
因为ab>0,所以当a=3时,b=4,则a+b=7,
当a=-3时,b=-4,则a+b=-7.
综上所述,a+b的值是7或-7.
8
解:(+4)×(-5)=-4×5=-20;
计算:
(1)(+4)×(-5);
(2)(-0.125)×(-8);
(4)0×(-13.52);
(6)(-1)×a.
(-0.125)×(-8)=0.125×8=1;
0×(-13.52)=0;
(-1)×a=-a.
9
D
10
C
若数a,b互为倒数,则( )
A.a-b=0 B.ab=1
C.a+b=0 D.ab=-1
11
B
下列叙述中错误的个数是( )
①任何有理数都有倒数
②互为倒数的两个数的积为1
③若a>0,b<0,则ab<0
④若a+b=0,则ab<0
A.1 B.2 C.3 D.4
12
B
【点拨】①任何非0的有理数都有倒数;②互为倒数的两个数的积为1;③若a>0,b<0,则ab<0;④若a+b=0,则ab≤0.故①④错误.
13
求下列各数的倒数.
14
下列说法中,正确的是( )
①两个正数中倒数大的反而小;
②两个负数中倒数大的反而小;
③两个有理数中倒数大的反而小;
④两个符号相同的有理数中倒数大的反而小.
A.①②④ B.① C.①②③ D.①④
A
错解:C
诊断:只要两个数同号,那么倒数大的反而小,未限定符号时,不能说哪个大.
正解:A
计算:
15
原式=4+1=5;
(3)4+(-0.5)×(-2);
(4)-3-0.125×8.
原式=-3-1=-4.
一辆出租车在一条东西走向的大街上行驶,这辆出租车连续送客20次,其中8次向东行驶,12次向西行驶,向东每次行驶10 km,向西每次行驶7 km.
16
(1)该出租车连续20次送客后,停在何处?
(2)该出租车一共行驶了多少千米的路程?
解:以向东为正方向,
则8×(+10)+12×(-7)=80-84=-4(km).
即该出租车停在出发点西边4 km处.
8×|+10|+12×|-7|=80+84=164(km).
故该出租车一共行驶了164 km的路程.
17
【点拨】本题运用分类讨论思想,x的绝对值是分
x=2和x=-2两种情况讨论.
解:因为a,b互为相反数,c,d互为倒数,x的绝对值是2.所以a+b=0,cd=1,x=2或x=-2.
18
规定一种新运算“*”,两数a,b通过“*”运算得(a+2)×2-b,即a*b=(a+2)×2-b,例如:3*5=(3+2)×2-5=10-5=5.根据上面的规定解答下题:
(1)求7*(-3)的值;
(2)7*(-3)与(-3)*7的值相等吗?
解:7*(-3)=(7+2)×2-(-3)=21.
因为(-3)*7=[(-3)+2]×2-7=-9,所以7*(-3)与(-3)*7的值不相等.
