海口市2012年高中数学青年教师课堂教学评比材料:课题:独立重复试验与二项分布
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:课题:独立重复试验与二项分布 |

|
|
| 格式 | zip | ||
| 文件大小 | 66.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 00:00:00 | ||
图片预览



文档简介
课题:独立重复试验与二项分布
人教A版选修2-3第二章第二单元第三课时
授课教师:海南海政学校 向旭明
一、教学目标
●知识与技能:
理解n次独立重复试验及二项分布模型,会判断一个具体问题是否服从二项分布,培养学生的自主学习能力、数学建摸能力,并能解决相应的实际问题。
●过程与方法:
通过主动探究、自主合作、相互交流,从具体事例中归纳出数学概念,使学生充分体会知识的发现过程,并渗透由特殊到一般,由具体到抽象的数学思想方法。
●情感态度与价值观:
使学生体会数学的理性与严谨,了解数学来源于实际,应用于实际的唯物主义思想,培养学生对新知识的科学态度,勇于探索和敢于创新的精神。
二、教学重点、难点
重点:独立重复试验、二项分布的理解及应用二项分布模型解决一些简单的实际问题。
难点:二项分布模型的构建。
三、教学方法与手段
教学方法:诱思探究教学法
学习方法:自主探究、观察发现、合作交流、归纳总结。
教学手段:多媒体辅助教学
四、教学过程
环节 教学设计 师生互动
创设情景导入新课 心理测试:游戏:有四张卡片,正反排列,同学们猜想下我会怎么放至少猜对二个你才为胜利(请看幻灯片演示)反面反面正面正面问题1: 前一次猜测的结果是否影响后一次的猜测?也就是每次猜测是否相互独立?每次试验有几种结果问题2:每次猜测,猜对的概率P= ,猜错的概率是q=1-p= 学生回答这个问题的同时,可以初步体验独立重复试验模型,为定义的提出作好铺垫。引起学生的好奇,激发学习和探究知识的兴趣。
师生互动探究新知 探究一 独立重复试验思考:在同等条件下,将一枚硬币重复抛掷100次,记Ai(i=1,2,…,100)表示“第i次抛掷硬币正面朝上”,那么事件A1,A2,…,A100两两之间是否相互独立?每次试验结果有几种结果? 思考:在同等条件下,某人连续射击20次,记Ai(i=1,2,…,20)表示“第i次射中”,那么事件A1,A2,…,A20两两之间是否相互独立?每次试验结果有几种结果? 相同 不同点 在满足学生的好奇之后让学生对这两个例子进行对比分析,目的是让学生进一步体验独立重复试验模型,并得出其特征,使定义的提出水到渠成从探究游戏中的第二个问题入手,引导学生合作探索新知识,,也符合学生的认知规律。同时突出本节课重点,也突破了难点。
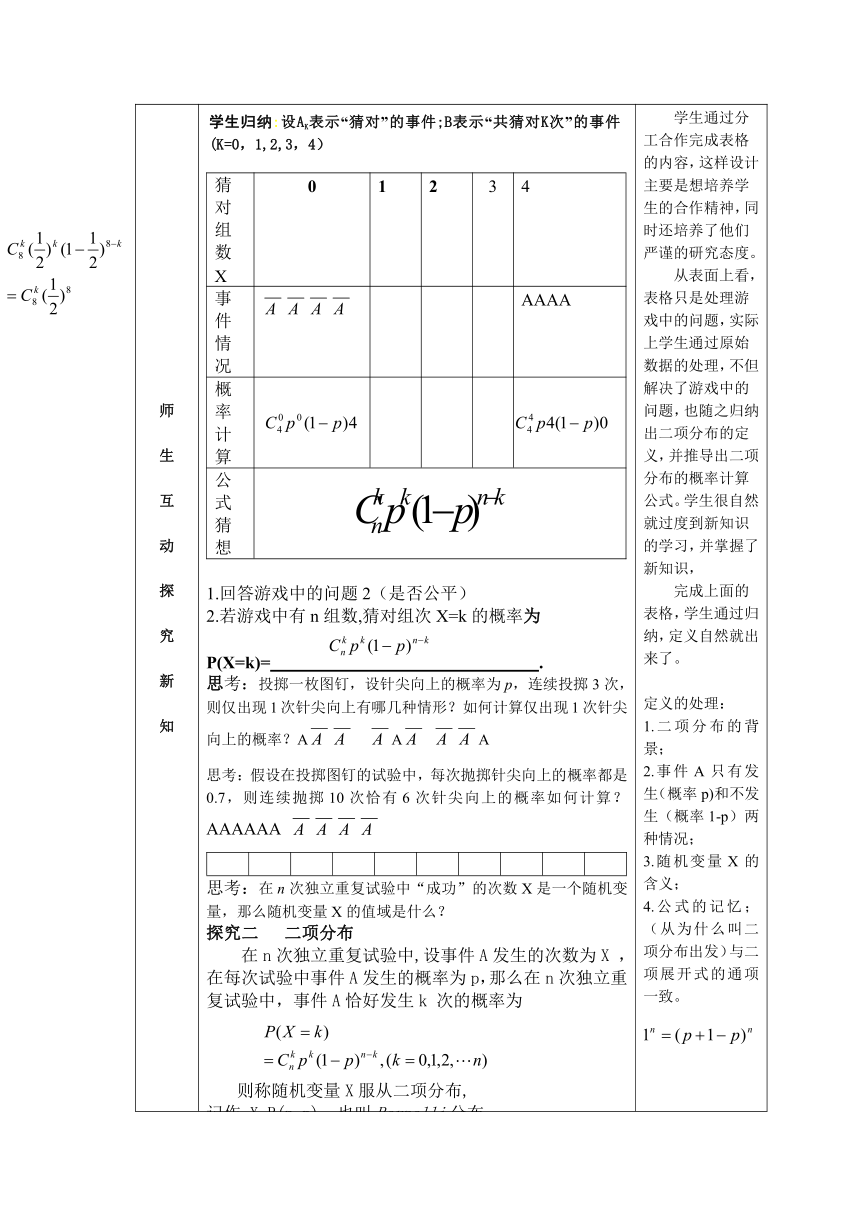
师生互动探究新知 猜对组数X01234事件情况AAAA概率计算公式猜想1.回答游戏中的问题2(是否公平)2.若游戏中有n组数,猜对组次X=k的概率为P(X=k)= .思考:投掷一枚图钉,设针尖向上的概率为p,连续投掷3次,则仅出现1次针尖向上有哪几种情形?如何计算仅出现1次针尖向上的概率?A A A思考:假设在投掷图钉的试验中,每次抛掷针尖向上的概率都是0.7,则连续抛掷10次恰有6次针尖向上的概率如何计算? AAAAAA 思考:在n次独立重复试验中“成功”的次数X是一个随机变量,那么随机变量X的值域是什么?探究二 二项分布在n次独立重复试验中,设事件A发生的次数为X ,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k 次的概率为 则称随机变量X服从二项分布, 记作 XB(n,p),也叫Bernolli分布。 学生通过分工合作完成表格的内容,这样设计主要是想培养学生的合作精神,同时还培养了他们严谨的研究态度。 从表面上看,表格只是处理游戏中的问题,实际上学生通过原始数据的处理,不但解决了游戏中的问题,也随之归纳出二项分布的定义,并推导出二项分布的概率计算公式。学生很自然就过度到新知识的学习,并掌握了新知识,完成上面的表格,学生通过归纳,定义自然就出来了。定义的处理:1.二项分布的背景;2.事件A只有发生(概率p)和不发生(概率1-p)两种情况;3.随机变量X的含义;4.公式的记忆;(从为什么叫二项分布出发)与二项展开式的通项一致。
知识应用 探究三 二项分布的运用例题1:某射手每次射击击中目标的概率是0.8 。求这名射手在10次射击中,(1)恰有8次击中目标的概率;(2)至少有8次击中目标的概率;(3)射中目标的次数X的分布列. (4)要保证击中目标概率大于0.98,至少应射击多少次?(结果保留两个有效数字)解:设X为击中目标的次数,则X~B (10, 0.8 ) . (1)在 10 次射击中,恰有 8 次击中目标的概率为 P (X = 8 ) =.(2)在 10 次射击中,至少有 8 次击中目标的概率为 P (X≥8) = P (X = 8) + P ( X = 9 ) + P ( X = 10 ) .(3)X012345678910P(4)设至少射击次,才能保证的保证击中目标概率大于0.98.∵射击次相当于次独立重复试验,记事件=“击中目标的事件”,则.∴.由题意,令,所以,两边取常用对数得,.即,∴,且,所以取. 第(1)、(2)问为课本的例4。教学中注意:1.为什么可以看成二项分布的模型;2.计算借助计算器;3.计算结果的解释;4.第(3)、(4)问有助学生更深刻理解二项分布。例2选自生活中与同学们密切的比赛的胜负,更好联系生活,解决实际生活问题思考题通过几种分布的类比,加深学生对二项分布的理解。
解决练习巩固新知 例题2:实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).(1)试分别求甲打完3局、4局、5局才能取胜的概率.(2)按比赛规则甲获胜的概率.解:甲、乙两队实力相等,所以每局比赛甲获胜的概率为,乙获胜的概率为.记事件=“甲打完3局才能取胜”,记事件=“甲打完4局才能取胜”,记事件=“甲打完5局才能取胜”.①甲打完3局取胜,相当于进行3次独立重复试验,且每局比赛甲均取胜∴甲打完3局取胜的概率为.②甲打完4局才能取胜,相当于进行4次独立重复试验,且甲第4局比赛取胜,前3局为2胜1负∴甲打完4局才能取胜的概率为.③甲打完5局才能取胜,相当于进行5次独立重复试验,且甲第5局比赛取胜,前4局恰好2胜2负∴甲打完5局才能取胜的概率为.(2)事件=“按比赛规则甲获胜”,则,又因为事件、、彼此互斥,故.答:按比赛规则甲获胜的概率为.随堂训练1.将一枚硬币连续抛掷5次,则正面向上的次数X的分布为( )A X~B ( 5,0.5 ) B X~B (0.5,5 )C X~B ( 2,0.5 ) D X~B ( 5,1 ) 2.随机变量X~B ( 3, 0.6 ) ,P ( X=1 ) =( )A 0.192 B 0.288 C 0.648 D 0.2543.某人考试,共有5题,解对4题为及格,若他解一道题正确率为0.6,则他及格概率( )A B C D 4. 某人掷一粒骰子6次,有4次以上出现5点或6点时为赢,则这人赢的可能性有多大? 。此部分以填空和问题的形式呈现,主要引导学生发现规律、得出结论,让学生经历由量变到质变、知识升华的过程,体验成功的喜悦,激活潜在的学习热情
环节 教学设计 师生互动
课堂小结,感悟收获 (1)知识小结: 1.在独立重复试验中,若每次试验结果只有事件A发生或不发生两种可能,则事件A发生的次数服从二项分布;… 2.二项分布B(n,p)中有两个参数,其中n是独立重复试验的总次数,p是每次试验事件A发生的概率,书写时n在左,p在右. 3.二项分布是来自于独立重复试验的一个概率模型,对于求在n次独立重复试验中,事件A恰好发生k次的概率,就直接利用概率公式求解. (2)能力总结:① 分清事件类型;② 转化复杂问题为基本的互斥事件与相互独立事件.(3)思想、方法: ① 分类讨论、归纳与演绎的方法; ② 辩证思想. 作业布置:书面作业:P60 A组2,3 ;B组 1,3阅读作业: 教材本节P59探究与发现; 。课堂小结与作业布置突出本节课知识点,适量,达到复习巩固的目的,又兼顾学有余力的同学有自由发展的空间,培养其探索精神和创新能力.
课外探究,巩固提高 课外探究:“三个臭皮匠能顶一个诸葛亮”吗 刘备帐下诸葛亮以聪明著称,假定对某事进行决策时,三个臭皮匠贡献正确意见的概率为0.6,诸葛亮贡献正确意见的概率为0.9.现为此事可行与否而征求意见作出决策,求作出正确决策的概率. 课外探究的题目富有趣味性且具有弹性,使学有余力的同学的创造力得到进一步发挥。
附:板书设计与时间安排
板书设计
板 书 设 计 独立重复试验与二项分布 探究一 独立重复试验在相同的条件下重复做的n次试验叫做n次独立重复试验 探究二 二项分布XB(n,p)k=0,1,2,…,n.探究三 二项分布的应用 小结:……… 作业:1)书面作业:P60A组2,3 ;B组 1,3 2)阅读作业: 教材本节P57探究与发现;
“硬币”与“射击”
“100”与“20”
…… ……
1.重复做同一件事
2.前提条件相同
3.都有两个对立的结果
相同条件,N次重复,相互独立
:
分小组合作、讨论、交流.,再以组为单位得出结论
此游戏是否可以看成是独立重复试验?
游戏中,我们用X表示猜对的组数,下面分组探讨X的取值和相应的概率,完成下表。
定义:在相同条件下重复做的n次试验称为n次独立重复试验。
学生归纳:
学生归纳:设AK表示“猜对”的事件;B表示“共猜对K次”的事件(K=0,1,2,3,4)
人教A版选修2-3第二章第二单元第三课时
授课教师:海南海政学校 向旭明
一、教学目标
●知识与技能:
理解n次独立重复试验及二项分布模型,会判断一个具体问题是否服从二项分布,培养学生的自主学习能力、数学建摸能力,并能解决相应的实际问题。
●过程与方法:
通过主动探究、自主合作、相互交流,从具体事例中归纳出数学概念,使学生充分体会知识的发现过程,并渗透由特殊到一般,由具体到抽象的数学思想方法。
●情感态度与价值观:
使学生体会数学的理性与严谨,了解数学来源于实际,应用于实际的唯物主义思想,培养学生对新知识的科学态度,勇于探索和敢于创新的精神。
二、教学重点、难点
重点:独立重复试验、二项分布的理解及应用二项分布模型解决一些简单的实际问题。
难点:二项分布模型的构建。
三、教学方法与手段
教学方法:诱思探究教学法
学习方法:自主探究、观察发现、合作交流、归纳总结。
教学手段:多媒体辅助教学
四、教学过程
环节 教学设计 师生互动
创设情景导入新课 心理测试:游戏:有四张卡片,正反排列,同学们猜想下我会怎么放至少猜对二个你才为胜利(请看幻灯片演示)反面反面正面正面问题1: 前一次猜测的结果是否影响后一次的猜测?也就是每次猜测是否相互独立?每次试验有几种结果问题2:每次猜测,猜对的概率P= ,猜错的概率是q=1-p= 学生回答这个问题的同时,可以初步体验独立重复试验模型,为定义的提出作好铺垫。引起学生的好奇,激发学习和探究知识的兴趣。
师生互动探究新知 探究一 独立重复试验思考:在同等条件下,将一枚硬币重复抛掷100次,记Ai(i=1,2,…,100)表示“第i次抛掷硬币正面朝上”,那么事件A1,A2,…,A100两两之间是否相互独立?每次试验结果有几种结果? 思考:在同等条件下,某人连续射击20次,记Ai(i=1,2,…,20)表示“第i次射中”,那么事件A1,A2,…,A20两两之间是否相互独立?每次试验结果有几种结果? 相同 不同点 在满足学生的好奇之后让学生对这两个例子进行对比分析,目的是让学生进一步体验独立重复试验模型,并得出其特征,使定义的提出水到渠成从探究游戏中的第二个问题入手,引导学生合作探索新知识,,也符合学生的认知规律。同时突出本节课重点,也突破了难点。
师生互动探究新知 猜对组数X01234事件情况AAAA概率计算公式猜想1.回答游戏中的问题2(是否公平)2.若游戏中有n组数,猜对组次X=k的概率为P(X=k)= .思考:投掷一枚图钉,设针尖向上的概率为p,连续投掷3次,则仅出现1次针尖向上有哪几种情形?如何计算仅出现1次针尖向上的概率?A A A思考:假设在投掷图钉的试验中,每次抛掷针尖向上的概率都是0.7,则连续抛掷10次恰有6次针尖向上的概率如何计算? AAAAAA 思考:在n次独立重复试验中“成功”的次数X是一个随机变量,那么随机变量X的值域是什么?探究二 二项分布在n次独立重复试验中,设事件A发生的次数为X ,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k 次的概率为 则称随机变量X服从二项分布, 记作 XB(n,p),也叫Bernolli分布。 学生通过分工合作完成表格的内容,这样设计主要是想培养学生的合作精神,同时还培养了他们严谨的研究态度。 从表面上看,表格只是处理游戏中的问题,实际上学生通过原始数据的处理,不但解决了游戏中的问题,也随之归纳出二项分布的定义,并推导出二项分布的概率计算公式。学生很自然就过度到新知识的学习,并掌握了新知识,完成上面的表格,学生通过归纳,定义自然就出来了。定义的处理:1.二项分布的背景;2.事件A只有发生(概率p)和不发生(概率1-p)两种情况;3.随机变量X的含义;4.公式的记忆;(从为什么叫二项分布出发)与二项展开式的通项一致。
知识应用 探究三 二项分布的运用例题1:某射手每次射击击中目标的概率是0.8 。求这名射手在10次射击中,(1)恰有8次击中目标的概率;(2)至少有8次击中目标的概率;(3)射中目标的次数X的分布列. (4)要保证击中目标概率大于0.98,至少应射击多少次?(结果保留两个有效数字)解:设X为击中目标的次数,则X~B (10, 0.8 ) . (1)在 10 次射击中,恰有 8 次击中目标的概率为 P (X = 8 ) =.(2)在 10 次射击中,至少有 8 次击中目标的概率为 P (X≥8) = P (X = 8) + P ( X = 9 ) + P ( X = 10 ) .(3)X012345678910P(4)设至少射击次,才能保证的保证击中目标概率大于0.98.∵射击次相当于次独立重复试验,记事件=“击中目标的事件”,则.∴.由题意,令,所以,两边取常用对数得,.即,∴,且,所以取. 第(1)、(2)问为课本的例4。教学中注意:1.为什么可以看成二项分布的模型;2.计算借助计算器;3.计算结果的解释;4.第(3)、(4)问有助学生更深刻理解二项分布。例2选自生活中与同学们密切的比赛的胜负,更好联系生活,解决实际生活问题思考题通过几种分布的类比,加深学生对二项分布的理解。
解决练习巩固新知 例题2:实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).(1)试分别求甲打完3局、4局、5局才能取胜的概率.(2)按比赛规则甲获胜的概率.解:甲、乙两队实力相等,所以每局比赛甲获胜的概率为,乙获胜的概率为.记事件=“甲打完3局才能取胜”,记事件=“甲打完4局才能取胜”,记事件=“甲打完5局才能取胜”.①甲打完3局取胜,相当于进行3次独立重复试验,且每局比赛甲均取胜∴甲打完3局取胜的概率为.②甲打完4局才能取胜,相当于进行4次独立重复试验,且甲第4局比赛取胜,前3局为2胜1负∴甲打完4局才能取胜的概率为.③甲打完5局才能取胜,相当于进行5次独立重复试验,且甲第5局比赛取胜,前4局恰好2胜2负∴甲打完5局才能取胜的概率为.(2)事件=“按比赛规则甲获胜”,则,又因为事件、、彼此互斥,故.答:按比赛规则甲获胜的概率为.随堂训练1.将一枚硬币连续抛掷5次,则正面向上的次数X的分布为( )A X~B ( 5,0.5 ) B X~B (0.5,5 )C X~B ( 2,0.5 ) D X~B ( 5,1 ) 2.随机变量X~B ( 3, 0.6 ) ,P ( X=1 ) =( )A 0.192 B 0.288 C 0.648 D 0.2543.某人考试,共有5题,解对4题为及格,若他解一道题正确率为0.6,则他及格概率( )A B C D 4. 某人掷一粒骰子6次,有4次以上出现5点或6点时为赢,则这人赢的可能性有多大? 。此部分以填空和问题的形式呈现,主要引导学生发现规律、得出结论,让学生经历由量变到质变、知识升华的过程,体验成功的喜悦,激活潜在的学习热情
环节 教学设计 师生互动
课堂小结,感悟收获 (1)知识小结: 1.在独立重复试验中,若每次试验结果只有事件A发生或不发生两种可能,则事件A发生的次数服从二项分布;… 2.二项分布B(n,p)中有两个参数,其中n是独立重复试验的总次数,p是每次试验事件A发生的概率,书写时n在左,p在右. 3.二项分布是来自于独立重复试验的一个概率模型,对于求在n次独立重复试验中,事件A恰好发生k次的概率,就直接利用概率公式求解. (2)能力总结:① 分清事件类型;② 转化复杂问题为基本的互斥事件与相互独立事件.(3)思想、方法: ① 分类讨论、归纳与演绎的方法; ② 辩证思想. 作业布置:书面作业:P60 A组2,3 ;B组 1,3阅读作业: 教材本节P59探究与发现; 。课堂小结与作业布置突出本节课知识点,适量,达到复习巩固的目的,又兼顾学有余力的同学有自由发展的空间,培养其探索精神和创新能力.
课外探究,巩固提高 课外探究:“三个臭皮匠能顶一个诸葛亮”吗 刘备帐下诸葛亮以聪明著称,假定对某事进行决策时,三个臭皮匠贡献正确意见的概率为0.6,诸葛亮贡献正确意见的概率为0.9.现为此事可行与否而征求意见作出决策,求作出正确决策的概率. 课外探究的题目富有趣味性且具有弹性,使学有余力的同学的创造力得到进一步发挥。
附:板书设计与时间安排
板书设计
板 书 设 计 独立重复试验与二项分布 探究一 独立重复试验在相同的条件下重复做的n次试验叫做n次独立重复试验 探究二 二项分布XB(n,p)k=0,1,2,…,n.探究三 二项分布的应用 小结:……… 作业:1)书面作业:P60A组2,3 ;B组 1,3 2)阅读作业: 教材本节P57探究与发现;
“硬币”与“射击”
“100”与“20”
…… ……
1.重复做同一件事
2.前提条件相同
3.都有两个对立的结果
相同条件,N次重复,相互独立
:
分小组合作、讨论、交流.,再以组为单位得出结论
此游戏是否可以看成是独立重复试验?
游戏中,我们用X表示猜对的组数,下面分组探讨X的取值和相应的概率,完成下表。
定义:在相同条件下重复做的n次试验称为n次独立重复试验。
学生归纳:
学生归纳:设AK表示“猜对”的事件;B表示“共猜对K次”的事件(K=0,1,2,3,4)
