海口市2012年高中数学青年教师课堂教学评比材料:简单的线性规划问题课件
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:简单的线性规划问题课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
海南昌茂中学
肖 笛
§3.3.2简单的线性规划问题
第一课时
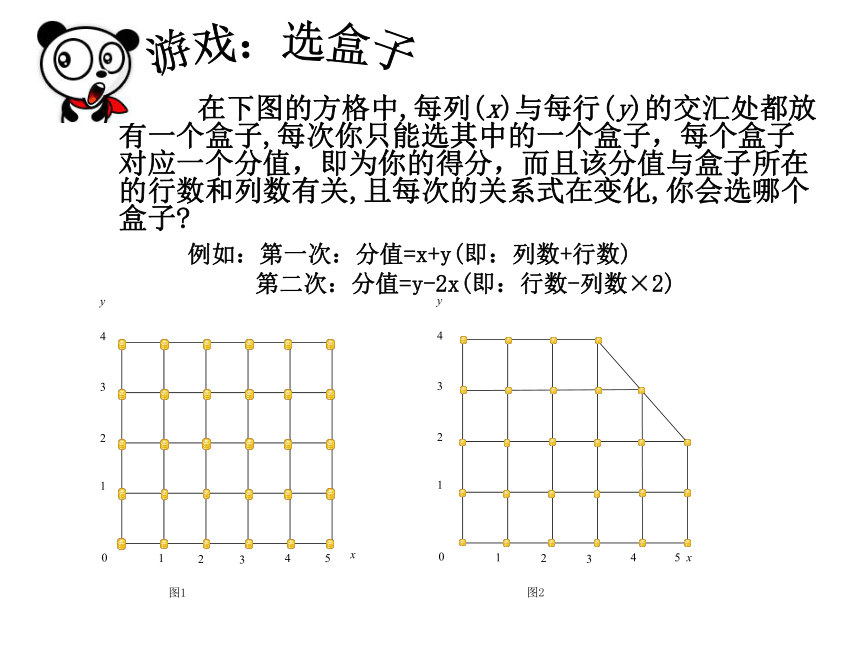
在下图的方格中,每列(x)与每行(y)的交汇处都放有一个盒子,每次你只能选其中的一个盒子,每个盒子对应一个分值,即为你的得分,而且该分值与盒子所在的行数和列数有关,且每次的关系式在变化,你会选哪个盒子
例如:第一次:分值=x+y(即:列数+行数)
第二次:分值=y-2x(即:行数-列数×2)
x
y
0
1
2
3
4
5
1
2
4
3
y
0
1
2
3
4
5 x
1
2
4
3
图1
图2
在图中找出2x+y的最大值
设b=2x+y,求2x+y的最大值即b的最大值
问题一:当b=6时,求x,y的值.
观察b=6时三个盒子所在点的位置关系。
(你能联想到什么?)
x
1
4
5
2
3
6
7
9
10
11
8
1
2
3
4
O
y
图3
三点共线 直线y=-2x+6
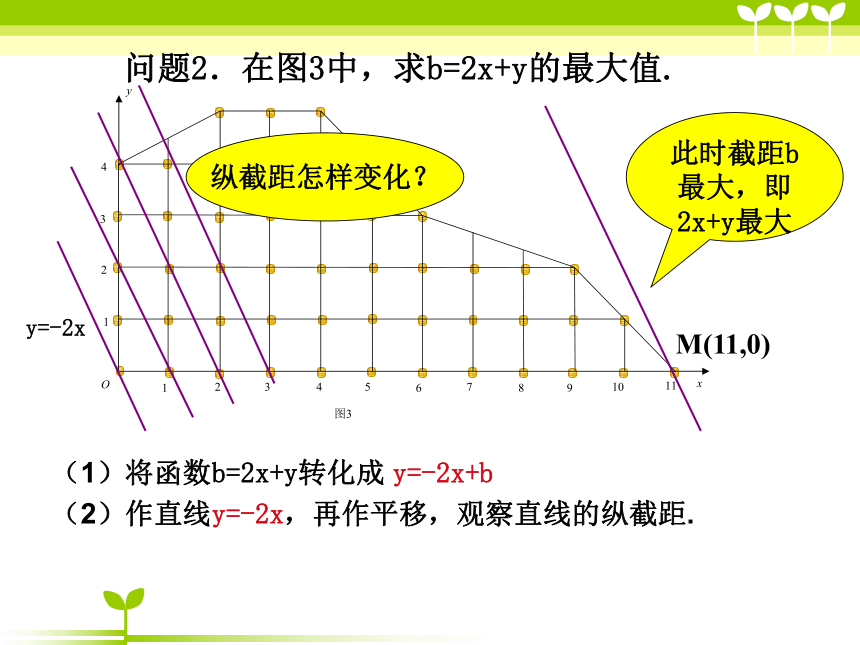
问题2.在图3中,求b=2x+y的最大值.
(1)将函数b=2x+y转化成 y=-2x+b
(2)作直线y=-2x,再作平移,观察直线的纵截距.
x
1
4
5
2
3
6
7
9
10
11
8
1
2
3
4
O
y
图3
纵截距怎样变化?
y=-2x
此时截距b最大,即2x+y最大
M(11,0)
实际问题
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
按甲、乙两种产品分别生产x、y件,由已知条件可得二元一次不等式组
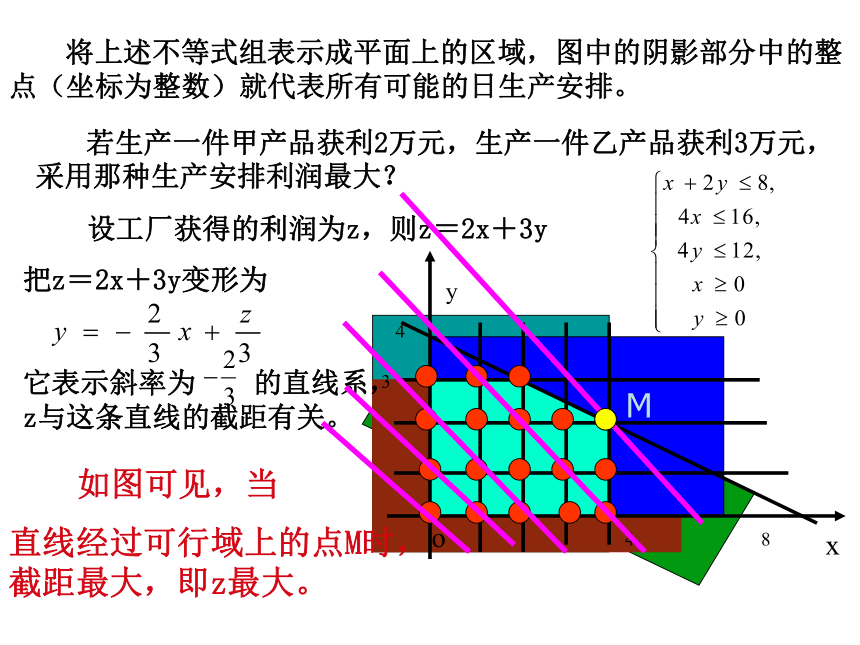
将上述不等式组表示成平面上的区域,图中的阴影部分中的整点(坐标为整数)就代表所有可能的日生产安排。
y
x
4
8
4
3
o
若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用那种生产安排利润最大?
设工厂获得的利润为z,则z=2x+3y
把z=2x+3y变形为
它表示斜率为 的直线系,z与这条直线的截距有关。
如图可见,当
直线经过可行域上的点M时,截距最大,即z最大。
M
二、基本概念
y
x
4
8
4
3
o
把求最大值或求最小值的的函数称为目标函数,因为它是关于变量x、y的一次解析式,又称线性目标函数。
满足线性约束的解
(x,y)叫做可行解。
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
一组关于变量x、y的一次不等式组,称为线性约束条件
由所有可行解组成的集合叫做可行域。
使目标函数取得最大
值或最小值的可行解叫做这个问题的最优解。
可行域
可行解
最优解
概念引入
(1)若问题中变量x、y满足不等式组, 则不等式组叫做变量
x、y的约束条件 ,这组约束条件都是关于x,y的一次不等
式,所以又称为线性约束条件
欲求最值的关于x、y的解析式叫做目标函数;
又因为这里的是关于变量x、y的一次解析式,所以又称
为线性目标函数。
求线性目标函数在线性约束条件下的最大值或最小值叫
做线性规划
(2)满足线性约束条件的解叫做可行解,
(3)由所有可行解组成的集合叫做可行域;
(4)其中使目标函数取得最大(小)值的可行解叫做最优解
练习题:
1、求z=2x+y的最大值,使x、y满足约束条件:
(2)作出直线y=-2x+z的图像
(3)可知z要求最大值,即将直线
平移到C点时。
(4)C点坐标为(2,-1),
求得则Zmax=2x+y=3
A
B
C
x
y
o
解:(1)画出可行区域
2、求z=3x+5y的最大值,使x、y满足约束条件:
作出直线3x+5y =z 的图像,可知直线经过A点时,Z取最大值;直线经过B点时,Z取最小值。
求得A(1.5,2.5),B(-2,-1),则Zmax=17,Zmin=-11。
x
y
o
A
B
C
解:作出平面区域
解答线性规划问题的步骤:
第一步:画根据约束条件画出可行
域;
第二步:作令z=0,画直线l0;
第三步:移观察,分析,平移直线l0,
从而找到最优解;
第四步:求求出目标函数的最大值或最
小值.
(1)约束条件--线性约束条件(一次的)
(2)目标函数--线性目标函数(一次的)
(3)线性规划
(4)可行解
(5)可行域
(6)最优解
小结:
概念
3x +2y=10
x +4y=11
必作:习题3.3--A组-3
选作:满足线性约束条件
的可行域中共有多
少个整数解。
作业:
1
2
2
3
3
1
4
4
5
5
x
y
0
x+4y≤11
3x +2y≤10
x>0
y>0
谢 谢
海南昌茂中学
肖 笛
§3.3.2简单的线性规划问题
第一课时
在下图的方格中,每列(x)与每行(y)的交汇处都放有一个盒子,每次你只能选其中的一个盒子,每个盒子对应一个分值,即为你的得分,而且该分值与盒子所在的行数和列数有关,且每次的关系式在变化,你会选哪个盒子
例如:第一次:分值=x+y(即:列数+行数)
第二次:分值=y-2x(即:行数-列数×2)
x
y
0
1
2
3
4
5
1
2
4
3
y
0
1
2
3
4
5 x
1
2
4
3
图1
图2
在图中找出2x+y的最大值
设b=2x+y,求2x+y的最大值即b的最大值
问题一:当b=6时,求x,y的值.
观察b=6时三个盒子所在点的位置关系。
(你能联想到什么?)
x
1
4
5
2
3
6
7
9
10
11
8
1
2
3
4
O
y
图3
三点共线 直线y=-2x+6
问题2.在图3中,求b=2x+y的最大值.
(1)将函数b=2x+y转化成 y=-2x+b
(2)作直线y=-2x,再作平移,观察直线的纵截距.
x
1
4
5
2
3
6
7
9
10
11
8
1
2
3
4
O
y
图3
纵截距怎样变化?
y=-2x
此时截距b最大,即2x+y最大
M(11,0)
实际问题
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
按甲、乙两种产品分别生产x、y件,由已知条件可得二元一次不等式组
将上述不等式组表示成平面上的区域,图中的阴影部分中的整点(坐标为整数)就代表所有可能的日生产安排。
y
x
4
8
4
3
o
若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用那种生产安排利润最大?
设工厂获得的利润为z,则z=2x+3y
把z=2x+3y变形为
它表示斜率为 的直线系,z与这条直线的截距有关。
如图可见,当
直线经过可行域上的点M时,截距最大,即z最大。
M
二、基本概念
y
x
4
8
4
3
o
把求最大值或求最小值的的函数称为目标函数,因为它是关于变量x、y的一次解析式,又称线性目标函数。
满足线性约束的解
(x,y)叫做可行解。
在线性约束条件下求线性目标函数的最大值或最小值问题,统称为线性规划问题。
一组关于变量x、y的一次不等式组,称为线性约束条件
由所有可行解组成的集合叫做可行域。
使目标函数取得最大
值或最小值的可行解叫做这个问题的最优解。
可行域
可行解
最优解
概念引入
(1)若问题中变量x、y满足不等式组, 则不等式组叫做变量
x、y的约束条件 ,这组约束条件都是关于x,y的一次不等
式,所以又称为线性约束条件
欲求最值的关于x、y的解析式叫做目标函数;
又因为这里的是关于变量x、y的一次解析式,所以又称
为线性目标函数。
求线性目标函数在线性约束条件下的最大值或最小值叫
做线性规划
(2)满足线性约束条件的解叫做可行解,
(3)由所有可行解组成的集合叫做可行域;
(4)其中使目标函数取得最大(小)值的可行解叫做最优解
练习题:
1、求z=2x+y的最大值,使x、y满足约束条件:
(2)作出直线y=-2x+z的图像
(3)可知z要求最大值,即将直线
平移到C点时。
(4)C点坐标为(2,-1),
求得则Zmax=2x+y=3
A
B
C
x
y
o
解:(1)画出可行区域
2、求z=3x+5y的最大值,使x、y满足约束条件:
作出直线3x+5y =z 的图像,可知直线经过A点时,Z取最大值;直线经过B点时,Z取最小值。
求得A(1.5,2.5),B(-2,-1),则Zmax=17,Zmin=-11。
x
y
o
A
B
C
解:作出平面区域
解答线性规划问题的步骤:
第一步:画根据约束条件画出可行
域;
第二步:作令z=0,画直线l0;
第三步:移观察,分析,平移直线l0,
从而找到最优解;
第四步:求求出目标函数的最大值或最
小值.
(1)约束条件--线性约束条件(一次的)
(2)目标函数--线性目标函数(一次的)
(3)线性规划
(4)可行解
(5)可行域
(6)最优解
小结:
概念
3x +2y=10
x +4y=11
必作:习题3.3--A组-3
选作:满足线性约束条件
的可行域中共有多
少个整数解。
作业:
1
2
2
3
3
1
4
4
5
5
x
y
0
x+4y≤11
3x +2y≤10
x>0
y>0
谢 谢
