2.2 探索轴对称的性质 课件(共16张PPT)
文档属性
| 名称 | 2.2 探索轴对称的性质 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 00:00:00 | ||
图片预览




文档简介
第二章 轴对称
2 探索轴对称的性质
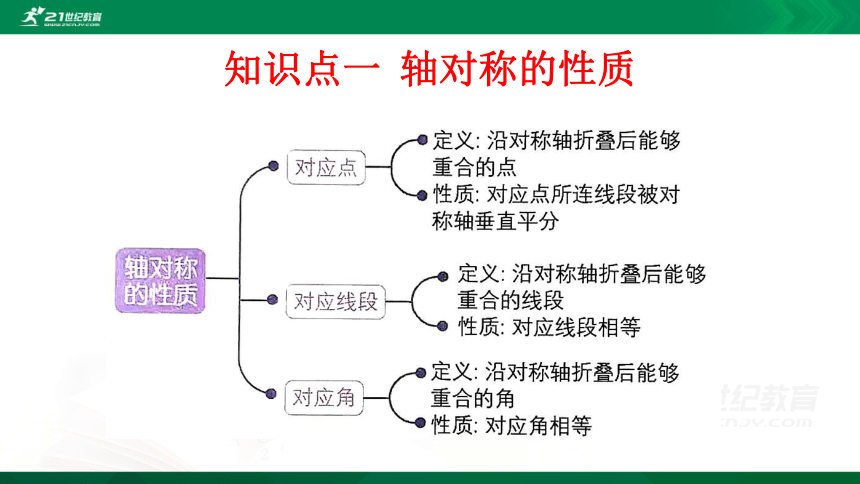
知识点一 轴对称的性质
温馨提示
(1)对称轴垂直平分对应点所连线段.
(2)对应点的连线互相平行(或在同一直线上).
(3)若两点所连线段被某直线垂直平分,则此直线为这两点的对称轴.
(4)成轴对称的两个图形,如果它们的对应线段或对应线段的延长线相交,那么交点一定在对称轴上;若不相交,则与对称轴平行.
解析
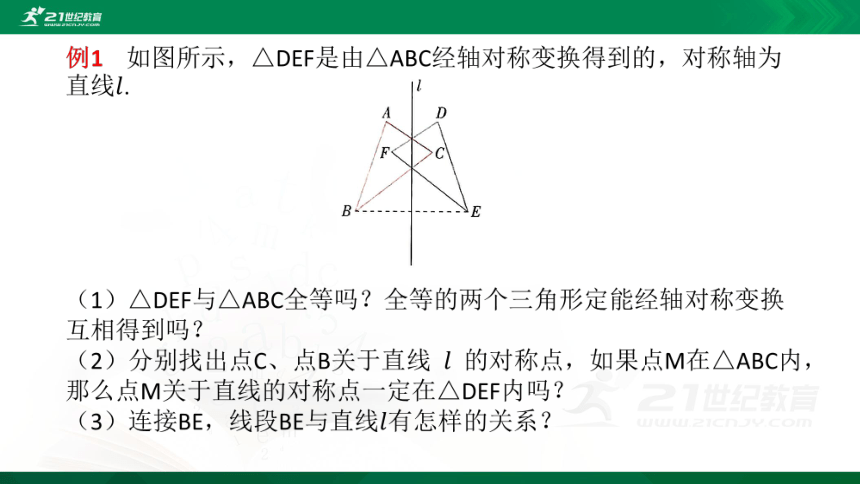
(1)△DEF与△ABC全等全等的两个三角形不一定能经轴对称变换互相得到,要看这两个三角形的位置关系.
知识点二 作已知图形关于某直线成轴对称的图形
画对称图形的步骤:
(1)找——在原图形上找特殊点(如线段的端点、线与线的交点等);
(2)作——作各个特殊点关于已知直线(对称轴)的对应点;
(3)连——按原图顺次连接各对应点.
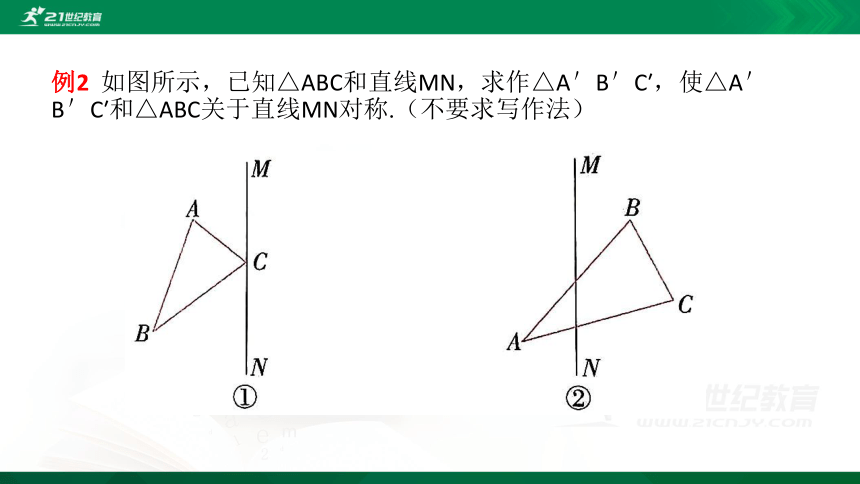
例2 如图所示,已知△ABC和直线MN,求作△A'B'C′,使△A'B'C′和△ABC关于直线MN对称.(不要求写作法)
分析 △ABC可以看做由三个特殊点A、B、C顺次连接得到的,所以只需要找到这三个点关于直线MN的对应点,顺次连接这些对应点,就可得到所求作的图形.
分析 △ABC可以看做由三个特殊点A、B、C顺次连接得到的,所以只需要找到这三个点关于直线MN的对应点,顺次连接这些对应点,就可得到所求作的图形.
解析 如图所示.
经典例题
题型一 利用轴对称的性质求角的度数
解析 因为△ABC与△A'B'C′关于直线对称,且∠A=102°,∠C′=25°,
所以∠C=25°,
所以∠B=180°-∠A-∠C=53°.
解析 因为△ABC与△A'B'C′关于直线对称,且∠A=102°,∠C′=25°,
所以∠C=25°,
所以∠B=180°-∠A-∠C=53°.
答案 53°
题型二 折叠中的轴对称
例2 如下图,将矩形纸片ABCD(图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片展平,那么∠AEF的度数为___________.
解析 根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,所以∠EAD=45°,如图所示,因为以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F,所以∠EA'F=∠FAE=45°,所以∠AFE=∠EFA′=(180°-45°)÷2=67.5°,所以∠AEF=∠FEA′=180-67.5-45°=67.5°.
故答案为67.5°.
解析 根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,所以∠EAD=45°,如图所示,因为以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F,所以∠EA'F=∠FAE=45°,所以∠AFE=∠EFA′=(180°-45°)÷2=67.5°,所以∠AEF=∠FEA′=180-67.5-45°=67.5°.
故答案为67.5°.
答案 67.5°
2 探索轴对称的性质
知识点一 轴对称的性质
温馨提示
(1)对称轴垂直平分对应点所连线段.
(2)对应点的连线互相平行(或在同一直线上).
(3)若两点所连线段被某直线垂直平分,则此直线为这两点的对称轴.
(4)成轴对称的两个图形,如果它们的对应线段或对应线段的延长线相交,那么交点一定在对称轴上;若不相交,则与对称轴平行.
解析
(1)△DEF与△ABC全等全等的两个三角形不一定能经轴对称变换互相得到,要看这两个三角形的位置关系.
知识点二 作已知图形关于某直线成轴对称的图形
画对称图形的步骤:
(1)找——在原图形上找特殊点(如线段的端点、线与线的交点等);
(2)作——作各个特殊点关于已知直线(对称轴)的对应点;
(3)连——按原图顺次连接各对应点.
例2 如图所示,已知△ABC和直线MN,求作△A'B'C′,使△A'B'C′和△ABC关于直线MN对称.(不要求写作法)
分析 △ABC可以看做由三个特殊点A、B、C顺次连接得到的,所以只需要找到这三个点关于直线MN的对应点,顺次连接这些对应点,就可得到所求作的图形.
分析 △ABC可以看做由三个特殊点A、B、C顺次连接得到的,所以只需要找到这三个点关于直线MN的对应点,顺次连接这些对应点,就可得到所求作的图形.
解析 如图所示.
经典例题
题型一 利用轴对称的性质求角的度数
解析 因为△ABC与△A'B'C′关于直线对称,且∠A=102°,∠C′=25°,
所以∠C=25°,
所以∠B=180°-∠A-∠C=53°.
解析 因为△ABC与△A'B'C′关于直线对称,且∠A=102°,∠C′=25°,
所以∠C=25°,
所以∠B=180°-∠A-∠C=53°.
答案 53°
题型二 折叠中的轴对称
例2 如下图,将矩形纸片ABCD(图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片展平,那么∠AEF的度数为___________.
解析 根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,所以∠EAD=45°,如图所示,因为以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F,所以∠EA'F=∠FAE=45°,所以∠AFE=∠EFA′=(180°-45°)÷2=67.5°,所以∠AEF=∠FEA′=180-67.5-45°=67.5°.
故答案为67.5°.
解析 根据题意:以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E,所以∠EAD=45°,如图所示,因为以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F,所以∠EA'F=∠FAE=45°,所以∠AFE=∠EFA′=(180°-45°)÷2=67.5°,所以∠AEF=∠FEA′=180-67.5-45°=67.5°.
故答案为67.5°.
答案 67.5°
