海口市2012年高中数学青年教师课堂教学评比材料:简单的线性规划问题
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:简单的线性规划问题 |  | |
| 格式 | zip | ||
| 文件大小 | 74.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 00:55:04 | ||
图片预览



文档简介
《简单的线性规划问题》教学设计
(人教A版高中课标教材数学必修5第三章第3.3.2节第1课时)
授课教师:肖 笛 海南昌茂中学
指导教师:冯建锁 海南昌茂中学
2012年3月
课题:简单的线性规划问题
海南昌茂中学 肖 笛
一、教材分析:
1、教材的地位与作用:
本节课是《普通高中课程标准实验教科书数学》人教A版必修5第三章《不等式》中3.3.2《简单的线性规划问题》的第一课时. 主要内容是线性规划的相关概念和简单的线性规划问题的解法.
线性规划是运筹学的一个重要分支,在实际生活中有着广泛的应用。本节内容是在学习了不等式、直线方程的基础上,利用不等式和直线方程的有关知识展开的,它是对二元一次不等式的深化和再认识、再理解。通过这一部分的学习,使学生进一步了解数学在解决实际问题中的应用,体验数形结合和化归的思想方法,培养学生学习数学的兴趣、应用数学的意识和解决实际问题的能力。
2、教学重点与难点:
重点: 画可行域;在可行域内,用图解法准确求得线性规划问题的最优解。
难点:用图解法求最优解的探索过程;数形结合思想的理解.
二、目标分析:
在新课标让学生经历“学数学、做数学、用数学”的理念指导下,本节课的教学目标分设为知识目标、能力目标和情感目标。
知识目标:
1、了解线性规划的意义,了解线性约束条件、线性目标函数、线性规划、可行解、可行域和最优解等概念;
2、理解线性规划问题的图解法;
3、会利用图解法求线性目标函数的最优解.
能力目标:
1、在应用图解法解题的过程中培养学生的观察能力、理解能力 。
2、在变式训练的过程中,培养学生的分析能力、探索能力。
3、在对具体事例的感性认识上升到对线性规划的理性认识过程中,培养学生运用数形结合思想解题的能力和化归能力。
情感目标:
1、让学生体验数学来源于生活,服务于生活,体验数学在建设节约型社会中的作用,品尝学习数学的乐趣。
2、让学生体验数学活动充满着探索与创造,培养学生勤于思考、勇于探索的精神;
3、让学生学会用运动观点观察事物,了解事物之间从一般到特殊、从特殊到一般的辨证关系,渗透辩证唯物主义认识论的思想。
三、过程分析:
数学教学是数学活动的教学。因此,我将整个教学过程分为以下六个教学环节:1、创设情境,激发欲望;2、分析问题,形成概念;3、变式演练,深入探究;4、反思过程,提炼方法;5、运用新知,解决问题;6、归纳总结,巩固提高。
(一)创设情境,引出课题
组织学生做选盒子的游戏活动.
在下图的方格中,每列(x)与每行(y)的交汇处都放有一个盒子,每次你只能选其中的一个盒子,每个盒子对应一个分值,即为你的得分,而且该分值与盒子所在的行数和列数有关,且每次的关系式在变化,你会选哪个盒子
例如: 第一次:分值= (即: 列数+行数)
第二次:分值= (即: 行数-列数×2)
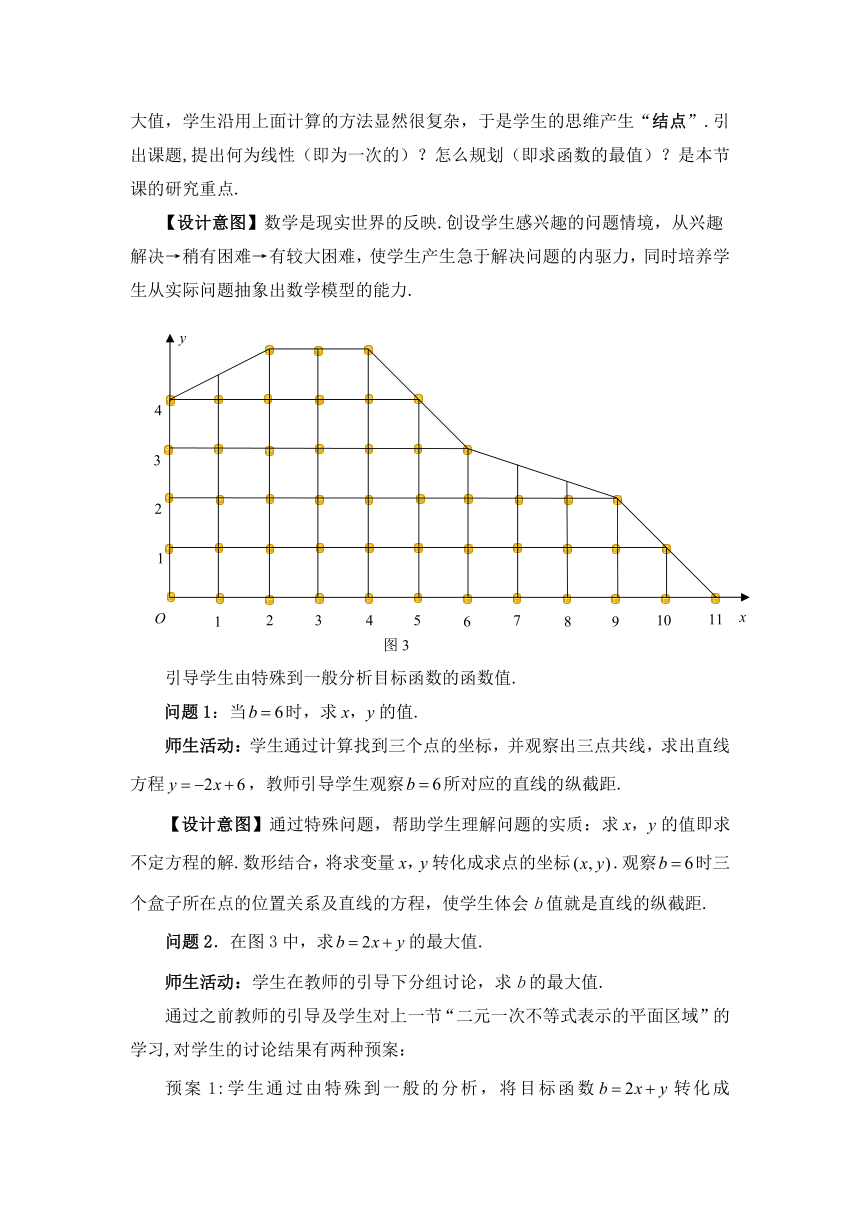
师生活动:教师组织学生做选盒子得分的游戏,学生用“运算----比较”的方法容易解决老师提出的问题.之后,给出图3,让学生在图中找函数的最大值,学生沿用上面计算的方法显然很复杂,于是学生的思维产生“结点”.引出课题,提出何为线性(即为一次的)?怎么规划(即求函数的最值)?是本节课的研究重点.
【设计意图】数学是现实世界的反映.创设学生感兴趣的问题情境,从兴趣解决→稍有困难→有较大困难,使学生产生急于解决问题的内驱力,同时培养学生从实际问题抽象出数学模型的能力.
引导学生由特殊到一般分析目标函数的函数值.
问题1:当时,求x,y的值.
师生活动:学生通过计算找到三个点的坐标,并观察出三点共线,求出直线方程,教师引导学生观察所对应的直线的纵截距.
【设计意图】通过特殊问题,帮助学生理解问题的实质:求x,y的值即求不定方程的解.数形结合,将求变量x,y转化成求点的坐标.观察时三个盒子所在点的位置关系及直线的方程,使学生体会b值就是直线的纵截距.
问题2.在图3中,求的最大值.
师生活动:学生在教师的引导下分组讨论,求b的最大值.
通过之前教师的引导及学生对上一节“二元一次不等式表示的平面区域”的学习,对学生的讨论结果有两种预案:
预案1:学生通过由特殊到一般的分析,将目标函数转化成,x,y在取得每个可行解时,b的取值就是直线过这个点时的纵截距,而所有这些直线都是平行的,因此只需平移直线看纵截距的最大值即可.
预案2:根据上一节“二元一次不等式(组)所表示的平面区域”的知识,学生认为b取最大值时x、y的取值一定在直线的右上方的位置,为此就依次在这些位置上画平行于的直线,只要上面有点就不停的画,直至最后一点.
师生活动:学生展示讨论结果,教师演示、分析,渗透转化和数形结合的数学思想.并对学生的结论作出总结,先作直线,再作平移,观察直线的纵截距.
【设计意图】由特殊到一般,利用数形结合,寻求解题思路.
变式1:将目标函数变成, 求b的最大值.
师生活动:通过学生将化成的形式,做直线并进行平移,观察纵截距的最大值的回答过程,教师强调解题步骤:画、作、移、求.
【设计意图】规范方法并检验学生对方法的理解程度,使学生感受由直线斜率的变化引起使取最大值的过程中点的变化.
(二)分析问题,形成概念
例1、某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有的日生产安排是什么?(1)设甲、乙两种产品分别生产x、y件,由已知条件可得二元一次不等式组:
(2)画出不等式组所表示的平面区域,如上图中阴影部分的整点(坐标为整数的点)就代表所有可能的日生产安排。(3)进一步,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?设生产甲产品x件乙产品y件时,工厂获得的利润为z,则z=2x+3y.这样,上述问题就转化为:当x、y满足不等式并且为非负整数时,z的最大值是多少?
变形----把, ( http: / / www. )这是斜率为,在轴上的截距为 的直线,当z变化时,可以得到一组互相平行的直线;
的平面区域内有公共点时,在区域内找一个点P,使直线经点P时截距最大
平移----通过平移找到满足上述条件的直线
表述----找到点M(4,2)后,求出对应的截距及z的值
概念引入
(1)若,式中变量x、y满足上面不等式组,
叫做变量x、y的约束条件 ,这组约束条件都是关于x,y的一次不等式(也可以是方程),所以又称为线性约束条件,叫做目标函数;又因为这里的是关于变量x、y的一次解析式,所以又称为线性目标函数。
(2)满足线性约束条件的解叫做可行解,
(3)由所有可行解组成的集合叫做可行域;
(4)其中使目标函数取得最大值(或最小值)的可行解叫做最优解
(三)变式演练,深入探究
练习1、求z=2x+y的最大值,使x、y满足约束条件:
(四)反思过程,提炼方法
解答线性规划问题的步骤:
第一步:画--根据约束条件画出可行域;
第二步:作--令z=0,作直线l0;
第三步:移--观察,分析,平移直线l0,从而找到最优解;
第四步:求--求出目标函数的最大值或最小值.
(五)运用新知,解决问题
练习2、求z=3x+5y的最大值,使x、y满足约束条件:
(六)归纳总结,巩固提高
由学生和教师共同总结本节课所学到的知识.
基本概念:6个 (1)约束条件--线性约束条件
(2)目标函数--线性目标函数
(3)线性规划
(4)可行解
(5)可行域
(6)最优解
解决线性规划问题的步骤:4步
第一步:画根据约束条件画出可行域;
第二步:作令z=0,画直线l0;
第三步:移观察,分析,平移直线l0,从而找到最优解;
第四步:求求出目标函数的最大值或最小值.
数学思想:运用化归与数形结合思想得到方法,以及如何通过数学建模解决实际问题.
课后作业—P93-3
板书设计
§3.3.2 简单的线性规划
线性:一次的 例1: 不等式(1) 解决线性规划问题的步骤
规划:求函数的最值 第一步:
(1)约束条件--线性约束条件 第二步:
(2)目标函数--线性目标函数 第三步:
(3)线性规划 (4)可行解 第四步:
(5)可行域 (6)最优解
海口市2012年高中数学青年教师
课堂教学微型课观摩与评比活动
优秀论文评选
x
y
0
1
2
3
4
5
1
2
4
3
y
0
1
2
3
4
5 x
1
2
4
3
图1
图2
x
1
4
5
2
3
6
7
9
10
11
8
1
2
3
4
O
y
图3
(人教A版高中课标教材数学必修5第三章第3.3.2节第1课时)
授课教师:肖 笛 海南昌茂中学
指导教师:冯建锁 海南昌茂中学
2012年3月
课题:简单的线性规划问题
海南昌茂中学 肖 笛
一、教材分析:
1、教材的地位与作用:
本节课是《普通高中课程标准实验教科书数学》人教A版必修5第三章《不等式》中3.3.2《简单的线性规划问题》的第一课时. 主要内容是线性规划的相关概念和简单的线性规划问题的解法.
线性规划是运筹学的一个重要分支,在实际生活中有着广泛的应用。本节内容是在学习了不等式、直线方程的基础上,利用不等式和直线方程的有关知识展开的,它是对二元一次不等式的深化和再认识、再理解。通过这一部分的学习,使学生进一步了解数学在解决实际问题中的应用,体验数形结合和化归的思想方法,培养学生学习数学的兴趣、应用数学的意识和解决实际问题的能力。
2、教学重点与难点:
重点: 画可行域;在可行域内,用图解法准确求得线性规划问题的最优解。
难点:用图解法求最优解的探索过程;数形结合思想的理解.
二、目标分析:
在新课标让学生经历“学数学、做数学、用数学”的理念指导下,本节课的教学目标分设为知识目标、能力目标和情感目标。
知识目标:
1、了解线性规划的意义,了解线性约束条件、线性目标函数、线性规划、可行解、可行域和最优解等概念;
2、理解线性规划问题的图解法;
3、会利用图解法求线性目标函数的最优解.
能力目标:
1、在应用图解法解题的过程中培养学生的观察能力、理解能力 。
2、在变式训练的过程中,培养学生的分析能力、探索能力。
3、在对具体事例的感性认识上升到对线性规划的理性认识过程中,培养学生运用数形结合思想解题的能力和化归能力。
情感目标:
1、让学生体验数学来源于生活,服务于生活,体验数学在建设节约型社会中的作用,品尝学习数学的乐趣。
2、让学生体验数学活动充满着探索与创造,培养学生勤于思考、勇于探索的精神;
3、让学生学会用运动观点观察事物,了解事物之间从一般到特殊、从特殊到一般的辨证关系,渗透辩证唯物主义认识论的思想。
三、过程分析:
数学教学是数学活动的教学。因此,我将整个教学过程分为以下六个教学环节:1、创设情境,激发欲望;2、分析问题,形成概念;3、变式演练,深入探究;4、反思过程,提炼方法;5、运用新知,解决问题;6、归纳总结,巩固提高。
(一)创设情境,引出课题
组织学生做选盒子的游戏活动.
在下图的方格中,每列(x)与每行(y)的交汇处都放有一个盒子,每次你只能选其中的一个盒子,每个盒子对应一个分值,即为你的得分,而且该分值与盒子所在的行数和列数有关,且每次的关系式在变化,你会选哪个盒子
例如: 第一次:分值= (即: 列数+行数)
第二次:分值= (即: 行数-列数×2)
师生活动:教师组织学生做选盒子得分的游戏,学生用“运算----比较”的方法容易解决老师提出的问题.之后,给出图3,让学生在图中找函数的最大值,学生沿用上面计算的方法显然很复杂,于是学生的思维产生“结点”.引出课题,提出何为线性(即为一次的)?怎么规划(即求函数的最值)?是本节课的研究重点.
【设计意图】数学是现实世界的反映.创设学生感兴趣的问题情境,从兴趣解决→稍有困难→有较大困难,使学生产生急于解决问题的内驱力,同时培养学生从实际问题抽象出数学模型的能力.
引导学生由特殊到一般分析目标函数的函数值.
问题1:当时,求x,y的值.
师生活动:学生通过计算找到三个点的坐标,并观察出三点共线,求出直线方程,教师引导学生观察所对应的直线的纵截距.
【设计意图】通过特殊问题,帮助学生理解问题的实质:求x,y的值即求不定方程的解.数形结合,将求变量x,y转化成求点的坐标.观察时三个盒子所在点的位置关系及直线的方程,使学生体会b值就是直线的纵截距.
问题2.在图3中,求的最大值.
师生活动:学生在教师的引导下分组讨论,求b的最大值.
通过之前教师的引导及学生对上一节“二元一次不等式表示的平面区域”的学习,对学生的讨论结果有两种预案:
预案1:学生通过由特殊到一般的分析,将目标函数转化成,x,y在取得每个可行解时,b的取值就是直线过这个点时的纵截距,而所有这些直线都是平行的,因此只需平移直线看纵截距的最大值即可.
预案2:根据上一节“二元一次不等式(组)所表示的平面区域”的知识,学生认为b取最大值时x、y的取值一定在直线的右上方的位置,为此就依次在这些位置上画平行于的直线,只要上面有点就不停的画,直至最后一点.
师生活动:学生展示讨论结果,教师演示、分析,渗透转化和数形结合的数学思想.并对学生的结论作出总结,先作直线,再作平移,观察直线的纵截距.
【设计意图】由特殊到一般,利用数形结合,寻求解题思路.
变式1:将目标函数变成, 求b的最大值.
师生活动:通过学生将化成的形式,做直线并进行平移,观察纵截距的最大值的回答过程,教师强调解题步骤:画、作、移、求.
【设计意图】规范方法并检验学生对方法的理解程度,使学生感受由直线斜率的变化引起使取最大值的过程中点的变化.
(二)分析问题,形成概念
例1、某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有的日生产安排是什么?(1)设甲、乙两种产品分别生产x、y件,由已知条件可得二元一次不等式组:
(2)画出不等式组所表示的平面区域,如上图中阴影部分的整点(坐标为整数的点)就代表所有可能的日生产安排。(3)进一步,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?设生产甲产品x件乙产品y件时,工厂获得的利润为z,则z=2x+3y.这样,上述问题就转化为:当x、y满足不等式并且为非负整数时,z的最大值是多少?
变形----把, ( http: / / www. )这是斜率为,在轴上的截距为 的直线,当z变化时,可以得到一组互相平行的直线;
的平面区域内有公共点时,在区域内找一个点P,使直线经点P时截距最大
平移----通过平移找到满足上述条件的直线
表述----找到点M(4,2)后,求出对应的截距及z的值
概念引入
(1)若,式中变量x、y满足上面不等式组,
叫做变量x、y的约束条件 ,这组约束条件都是关于x,y的一次不等式(也可以是方程),所以又称为线性约束条件,叫做目标函数;又因为这里的是关于变量x、y的一次解析式,所以又称为线性目标函数。
(2)满足线性约束条件的解叫做可行解,
(3)由所有可行解组成的集合叫做可行域;
(4)其中使目标函数取得最大值(或最小值)的可行解叫做最优解
(三)变式演练,深入探究
练习1、求z=2x+y的最大值,使x、y满足约束条件:
(四)反思过程,提炼方法
解答线性规划问题的步骤:
第一步:画--根据约束条件画出可行域;
第二步:作--令z=0,作直线l0;
第三步:移--观察,分析,平移直线l0,从而找到最优解;
第四步:求--求出目标函数的最大值或最小值.
(五)运用新知,解决问题
练习2、求z=3x+5y的最大值,使x、y满足约束条件:
(六)归纳总结,巩固提高
由学生和教师共同总结本节课所学到的知识.
基本概念:6个 (1)约束条件--线性约束条件
(2)目标函数--线性目标函数
(3)线性规划
(4)可行解
(5)可行域
(6)最优解
解决线性规划问题的步骤:4步
第一步:画根据约束条件画出可行域;
第二步:作令z=0,画直线l0;
第三步:移观察,分析,平移直线l0,从而找到最优解;
第四步:求求出目标函数的最大值或最小值.
数学思想:运用化归与数形结合思想得到方法,以及如何通过数学建模解决实际问题.
课后作业—P93-3
板书设计
§3.3.2 简单的线性规划
线性:一次的 例1: 不等式(1) 解决线性规划问题的步骤
规划:求函数的最值 第一步:
(1)约束条件--线性约束条件 第二步:
(2)目标函数--线性目标函数 第三步:
(3)线性规划 (4)可行解 第四步:
(5)可行域 (6)最优解
海口市2012年高中数学青年教师
课堂教学微型课观摩与评比活动
优秀论文评选
x
y
0
1
2
3
4
5
1
2
4
3
y
0
1
2
3
4
5 x
1
2
4
3
图1
图2
x
1
4
5
2
3
6
7
9
10
11
8
1
2
3
4
O
y
图3
