海口市2012年高中数学青年教师课堂教学评比材料:独立重复试验与二项分布课件
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:独立重复试验与二项分布课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 328.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 00:00:00 | ||
图片预览









文档简介
(共20张PPT)
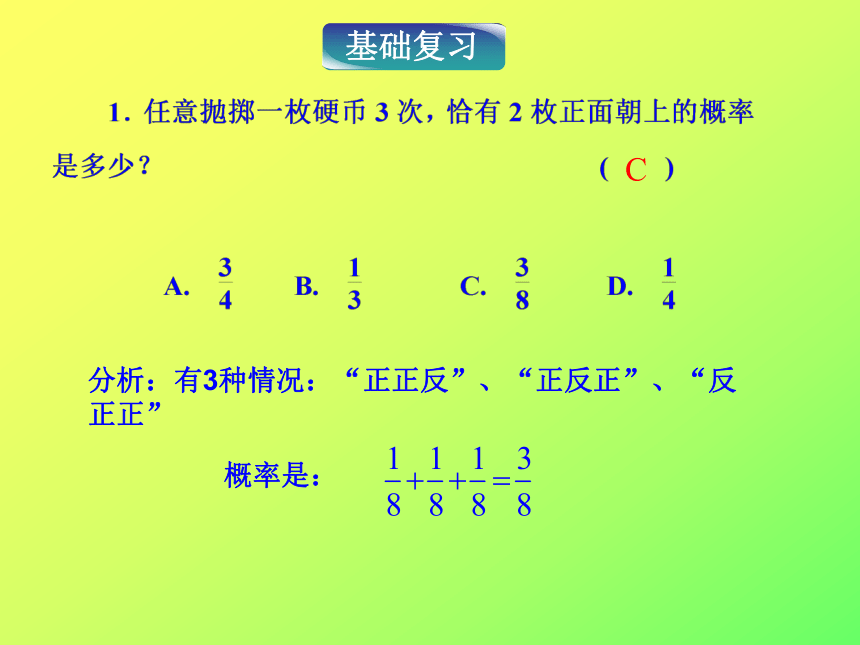
C
基础复习
分析:有3种情况:“正正反”、“正反正”、“反正正”
概率是:
概念复习
1.任意抛掷一枚硬币3次,恰有2枚正面朝上的概率是多少?
变式:
2.任意抛掷一枚硬币100次,恰有2枚正面朝上的概率是多少?
2.2.3 独立重复试验与二项分布
人教A版 选修2-3
海口实验中学 刘宸逸
1.任意抛掷一枚硬币3次,恰有2枚正面朝上的概率是多少?
变式:
2.任意抛掷一枚硬币100次,恰有2枚正面朝上的概率是多少?
复习引入
特点:
1)在相同的条件下重复地进行的一种试验;
2)任何一次试验中,A事件发生的概率相同,即相互
独立,互不影响试验的结果;
3)每次试验都只有两种结果,即事件要么发生,要么
不发生。
投掷一枚图钉,设针尖向上的概率为p,
则针尖向下的概率为q=1-p . 连续投掷
一枚图钉3次,仅出现一次针尖向上的概
率是多少?
分析:3次中仅出现1次针尖向上,有几种情况?
它们的概率是多少?
共有3种情况:
探究:
引申推广:若连续投掷n次,恰有k 次针尖向上的概率是多少?
连续投掷一枚图钉3次,出现k次针尖向上的概率是多少?
类似地
可以发现:
引申推广:
若连续掷n次,恰有k次针尖向上的概率是多少?
2、二项分布:
一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为
此时称随机变量X服从二项分布,记作X~B(n,p),并称p为成功概率。
注:
展开式中的第 项.
引申推广:若连续掷n次,恰有k次针尖向上的概率是多少?
2.任意抛掷一枚硬币100次,恰有2枚正面
朝上的概率是多少?
例4.某射手每次射击击中目标的概率是0 . 8.求这名 射手在 10 次射击中,
(1)恰有 8 次击中目标的概率;
(2)至少有 8 次击中目标的概率.(结果保留两个有效 数字.)
解:设X为击中目标的次数,则X~B (10, 0.8 ) .
(1)在 10 次射击中,恰有 8 次击中目标的概率为
P (X = 8 ) =
.
(2)在 10 次射击中,至少有 8 次击中目标的概率为
P (X≥8) = P (X = 8) + P ( X = 9 ) + P ( X = 10 )
练习1:一位病人服用某药品被治愈的概率为90%,求服用这种药的10位患有同样疾病的病人中至少有7人被治愈的概率.
分析: 至少有7人被治愈可看成事件A至少发生7次,故由在n次独立重复试验中某事件恰好发生k次的概率计算公式可求.
练习2. 某气象站天气预报的准确率为80%,计算:(结果保留到小数点后第2位)
(1)“5次预报中恰有2次准确”的概率;
(2)“5次预报中至少有2次准确”的概率.
【思路点拨】 由于5次预报是相互独立的,且结果只有两种(或准确或不准确),符合独立重复试验模型.
1.独立重复试验的概念及特点
3)每次试验都只有两种结果,即事件要么发生,要么不发生
2)各次试验中的事件是相互独立的
1)每次试验是在同样条件下进行
2.二项分布
今天我们学了一些什么
作业:
课本 P58 练习 1 P59 A组 3
谢谢指导!
C
基础复习
分析:有3种情况:“正正反”、“正反正”、“反正正”
概率是:
概念复习
1.任意抛掷一枚硬币3次,恰有2枚正面朝上的概率是多少?
变式:
2.任意抛掷一枚硬币100次,恰有2枚正面朝上的概率是多少?
2.2.3 独立重复试验与二项分布
人教A版 选修2-3
海口实验中学 刘宸逸
1.任意抛掷一枚硬币3次,恰有2枚正面朝上的概率是多少?
变式:
2.任意抛掷一枚硬币100次,恰有2枚正面朝上的概率是多少?
复习引入
特点:
1)在相同的条件下重复地进行的一种试验;
2)任何一次试验中,A事件发生的概率相同,即相互
独立,互不影响试验的结果;
3)每次试验都只有两种结果,即事件要么发生,要么
不发生。
投掷一枚图钉,设针尖向上的概率为p,
则针尖向下的概率为q=1-p . 连续投掷
一枚图钉3次,仅出现一次针尖向上的概
率是多少?
分析:3次中仅出现1次针尖向上,有几种情况?
它们的概率是多少?
共有3种情况:
探究:
引申推广:若连续投掷n次,恰有k 次针尖向上的概率是多少?
连续投掷一枚图钉3次,出现k次针尖向上的概率是多少?
类似地
可以发现:
引申推广:
若连续掷n次,恰有k次针尖向上的概率是多少?
2、二项分布:
一般地,在n次独立重复试验中,设事件A发生的次数为X,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k次的概率为
此时称随机变量X服从二项分布,记作X~B(n,p),并称p为成功概率。
注:
展开式中的第 项.
引申推广:若连续掷n次,恰有k次针尖向上的概率是多少?
2.任意抛掷一枚硬币100次,恰有2枚正面
朝上的概率是多少?
例4.某射手每次射击击中目标的概率是0 . 8.求这名 射手在 10 次射击中,
(1)恰有 8 次击中目标的概率;
(2)至少有 8 次击中目标的概率.(结果保留两个有效 数字.)
解:设X为击中目标的次数,则X~B (10, 0.8 ) .
(1)在 10 次射击中,恰有 8 次击中目标的概率为
P (X = 8 ) =
.
(2)在 10 次射击中,至少有 8 次击中目标的概率为
P (X≥8) = P (X = 8) + P ( X = 9 ) + P ( X = 10 )
练习1:一位病人服用某药品被治愈的概率为90%,求服用这种药的10位患有同样疾病的病人中至少有7人被治愈的概率.
分析: 至少有7人被治愈可看成事件A至少发生7次,故由在n次独立重复试验中某事件恰好发生k次的概率计算公式可求.
练习2. 某气象站天气预报的准确率为80%,计算:(结果保留到小数点后第2位)
(1)“5次预报中恰有2次准确”的概率;
(2)“5次预报中至少有2次准确”的概率.
【思路点拨】 由于5次预报是相互独立的,且结果只有两种(或准确或不准确),符合独立重复试验模型.
1.独立重复试验的概念及特点
3)每次试验都只有两种结果,即事件要么发生,要么不发生
2)各次试验中的事件是相互独立的
1)每次试验是在同样条件下进行
2.二项分布
今天我们学了一些什么
作业:
课本 P58 练习 1 P59 A组 3
谢谢指导!
