海口市2012年高中数学青年教师课堂教学评比材料:简单的线性规划教学设计
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:简单的线性规划教学设计 |  | |
| 格式 | zip | ||
| 文件大小 | 60.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 01:02:59 | ||
图片预览

文档简介
3.3.2 简单的线性规划问题(一)
海口市长流中学 殷海燕
教学目标 :
1、了解线性规划的意义,了解线性约束条件、线性目标函数、可行解、可行域和最优解等概念;理解线性规划问题的图解法;会利用图解法求线性目标函数的最优解。
2、在实验探究的过程中,让学生体验数学活动充满着探索与创造,培养学生的数据分析能力、探索能力、合情推理能力及动手操作、勇于探索的精神;
3、在应用图解法解题的过程中,培养学生运用数形结合思想解题的能力和化归能力,体验数学来源于生活,服务于生活,体验数学在建设节约型社会中的作用。
教学重点和难点:
教学重点:线性规划的图解法
教学难点:利用图解法求最优解,解决难点的方法是精确作图,利用数形结合的思想将代数问题几何化。
教学过程:
一.回顾旧知
二元一次不等式在平面直角坐标系中平面区域的确定方法
(线定界 点定域)
例如:
二元一次不等式组在平面直角坐标系中平面区域的确定方法
把上节课所留下的习题给出答案
二.新课
1.如果若干年后的你成为某工厂的厂长,你将会面对生产安排、资源利用、人力调配的问题……
从而提出引例
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时1h,每生产一件乙产品使用4个B配件并耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
引导学生自己阅读理解后,先列表,完成表格后,设出未知数,根据表格内的不等关系列出不等式。
数据分析表
每件耗时(h) A配件(个) B配件(个)
甲产品 1 4 0
乙产品 2 0 4
日生产满足
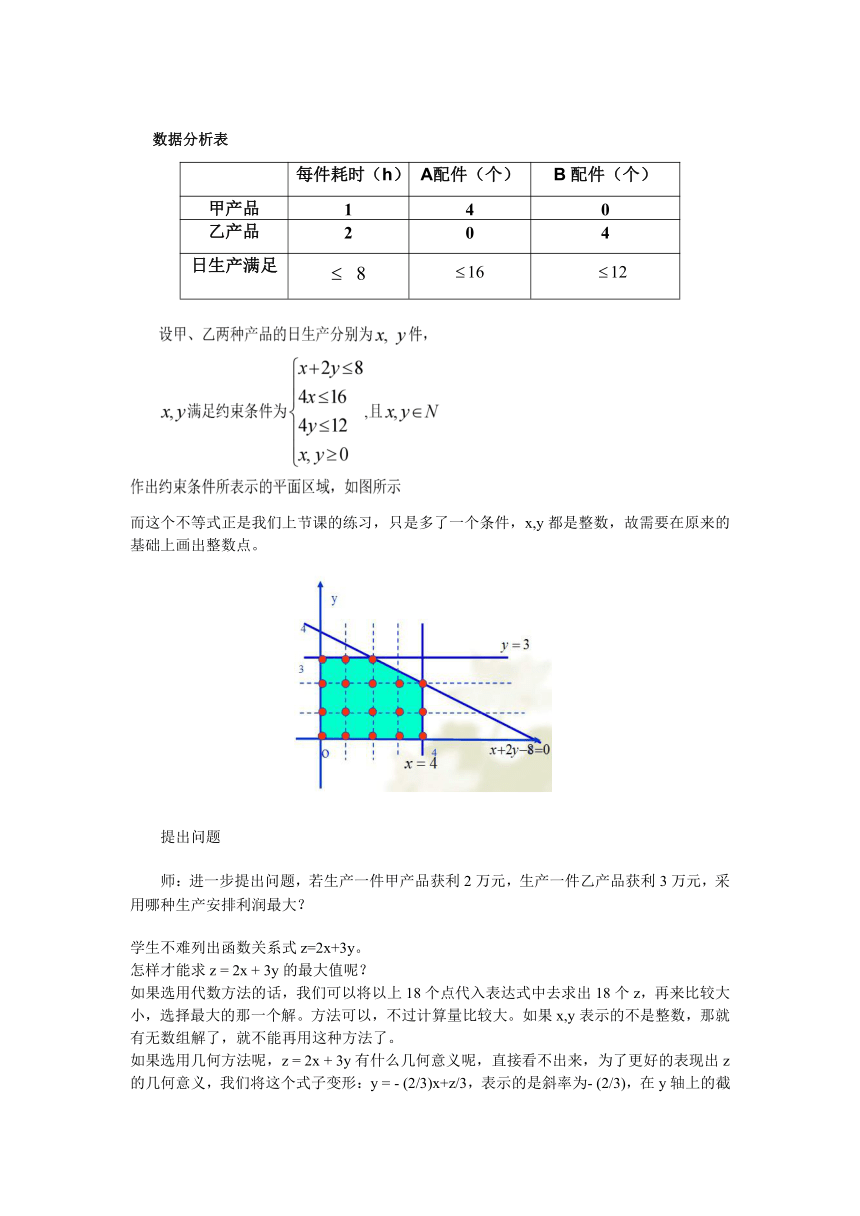
而这个不等式正是我们上节课的练习,只是多了一个条件,x,y都是整数,故需要在原来的基础上画出整数点。
提出问题
师:进一步提出问题,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
学生不难列出函数关系式z=2x+3y。
怎样才能求z = 2x + 3y的最大值呢?
如果选用代数方法的话,我们可以将以上18个点代入表达式中去求出18个z,再来比较大小,选择最大的那一个解。方法可以,不过计算量比较大。如果x,y表示的不是整数,那就有无数组解了,就不能再用这种方法了。
如果选用几何方法呢,z = 2x + 3y有什么几何意义呢,直接看不出来,为了更好的表现出z的几何意义,我们将这个式子变形:y = - (2/3)x+z/3,表示的是斜率为- (2/3),在y轴上的截距为z/3的直线。那么,z 的几何意义为这个直线在y轴上的截距的3倍,纵截距越大,z也越大。随着z的变化,就可以得到一组平行直线,由于斜率为- (2/3)是确定的,则只需再找一个点就可以确定z/3。当然这个点必须在这个确定的平面区域内,这个问题就转化成了在阴影部分找一点,过这个点作一条斜率为-2/3直线,使得它与y轴的截距最大。
我们可以先画出最特殊的一条y = - (2/3)x,(注意画图要准确,否则结果会有偏差)再将它平移,在与平面区域有交点的前提下,平移到它与y轴截距最大时,从而找到这个点。幻灯片示范,得到M点
答:每天生产甲产品4件,乙产品2件时,工厂可获得最大利润14万元
通过这个例子说明线性规划、线性约束条件、线性目标函数、可行解、可行域和最优解等概念。
从引例中总结
解线性规划问题的步骤:
1、 画出线性约束条件所表示的可行域;
2、 取目标函数z=0,过原点作相应的直线,平移该直线,观察确定区域内最优解的位置 ;
3、 通过解方程组求出最优解;
4、 作出答案。
探究:
提出问题:在引例的基础上,若生产一件甲产品获利1万元,生产一件乙产品获利3万元,采用哪种日生产安排利润最大?
求利润z=x+3y的最大值
类似于我们的例题,请学生自己完成,然后再对照答案。
三.练习
例题讲解完后,通过习题来巩固学生的知识
四.小结
线性规划、线性约束条件、线性目标函数、可行解、可行域和最优解等概念。
解线性规划问题的步骤:
1、 画出线性约束条件所表示的可行域;
2、 取目标函数z=0,过原点作相应的直线,平移该直线,观察确定区域内最优解的位置 ;
3、 通过解方程组求出最优解;
4、 作出答案。
五.作业:课本P91 练习题 1
六.板书设计
简单的线性规划
例题分析过程 解决线性规划的一般步骤1.234
海口市长流中学 殷海燕
教学目标 :
1、了解线性规划的意义,了解线性约束条件、线性目标函数、可行解、可行域和最优解等概念;理解线性规划问题的图解法;会利用图解法求线性目标函数的最优解。
2、在实验探究的过程中,让学生体验数学活动充满着探索与创造,培养学生的数据分析能力、探索能力、合情推理能力及动手操作、勇于探索的精神;
3、在应用图解法解题的过程中,培养学生运用数形结合思想解题的能力和化归能力,体验数学来源于生活,服务于生活,体验数学在建设节约型社会中的作用。
教学重点和难点:
教学重点:线性规划的图解法
教学难点:利用图解法求最优解,解决难点的方法是精确作图,利用数形结合的思想将代数问题几何化。
教学过程:
一.回顾旧知
二元一次不等式在平面直角坐标系中平面区域的确定方法
(线定界 点定域)
例如:
二元一次不等式组在平面直角坐标系中平面区域的确定方法
把上节课所留下的习题给出答案
二.新课
1.如果若干年后的你成为某工厂的厂长,你将会面对生产安排、资源利用、人力调配的问题……
从而提出引例
某工厂用A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件并耗时1h,每生产一件乙产品使用4个B配件并耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天工作8h计算,该厂所有可能的日生产安排是什么?
引导学生自己阅读理解后,先列表,完成表格后,设出未知数,根据表格内的不等关系列出不等式。
数据分析表
每件耗时(h) A配件(个) B配件(个)
甲产品 1 4 0
乙产品 2 0 4
日生产满足
而这个不等式正是我们上节课的练习,只是多了一个条件,x,y都是整数,故需要在原来的基础上画出整数点。
提出问题
师:进一步提出问题,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
学生不难列出函数关系式z=2x+3y。
怎样才能求z = 2x + 3y的最大值呢?
如果选用代数方法的话,我们可以将以上18个点代入表达式中去求出18个z,再来比较大小,选择最大的那一个解。方法可以,不过计算量比较大。如果x,y表示的不是整数,那就有无数组解了,就不能再用这种方法了。
如果选用几何方法呢,z = 2x + 3y有什么几何意义呢,直接看不出来,为了更好的表现出z的几何意义,我们将这个式子变形:y = - (2/3)x+z/3,表示的是斜率为- (2/3),在y轴上的截距为z/3的直线。那么,z 的几何意义为这个直线在y轴上的截距的3倍,纵截距越大,z也越大。随着z的变化,就可以得到一组平行直线,由于斜率为- (2/3)是确定的,则只需再找一个点就可以确定z/3。当然这个点必须在这个确定的平面区域内,这个问题就转化成了在阴影部分找一点,过这个点作一条斜率为-2/3直线,使得它与y轴的截距最大。
我们可以先画出最特殊的一条y = - (2/3)x,(注意画图要准确,否则结果会有偏差)再将它平移,在与平面区域有交点的前提下,平移到它与y轴截距最大时,从而找到这个点。幻灯片示范,得到M点
答:每天生产甲产品4件,乙产品2件时,工厂可获得最大利润14万元
通过这个例子说明线性规划、线性约束条件、线性目标函数、可行解、可行域和最优解等概念。
从引例中总结
解线性规划问题的步骤:
1、 画出线性约束条件所表示的可行域;
2、 取目标函数z=0,过原点作相应的直线,平移该直线,观察确定区域内最优解的位置 ;
3、 通过解方程组求出最优解;
4、 作出答案。
探究:
提出问题:在引例的基础上,若生产一件甲产品获利1万元,生产一件乙产品获利3万元,采用哪种日生产安排利润最大?
求利润z=x+3y的最大值
类似于我们的例题,请学生自己完成,然后再对照答案。
三.练习
例题讲解完后,通过习题来巩固学生的知识
四.小结
线性规划、线性约束条件、线性目标函数、可行解、可行域和最优解等概念。
解线性规划问题的步骤:
1、 画出线性约束条件所表示的可行域;
2、 取目标函数z=0,过原点作相应的直线,平移该直线,观察确定区域内最优解的位置 ;
3、 通过解方程组求出最优解;
4、 作出答案。
五.作业:课本P91 练习题 1
六.板书设计
简单的线性规划
例题分析过程 解决线性规划的一般步骤1.234
