海口市2012年高中数学青年教师课堂教学评比材料:必修4. 2.4.1平面向量数量积的物理背景及其含义 课件
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:必修4. 2.4.1平面向量数量积的物理背景及其含义 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 454.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 00:00:00 | ||
图片预览




文档简介
(共13张PPT)
2.4.1平面向量数量积的物理背景及其含义
湖南师大附中海口中学
瞿朝辉
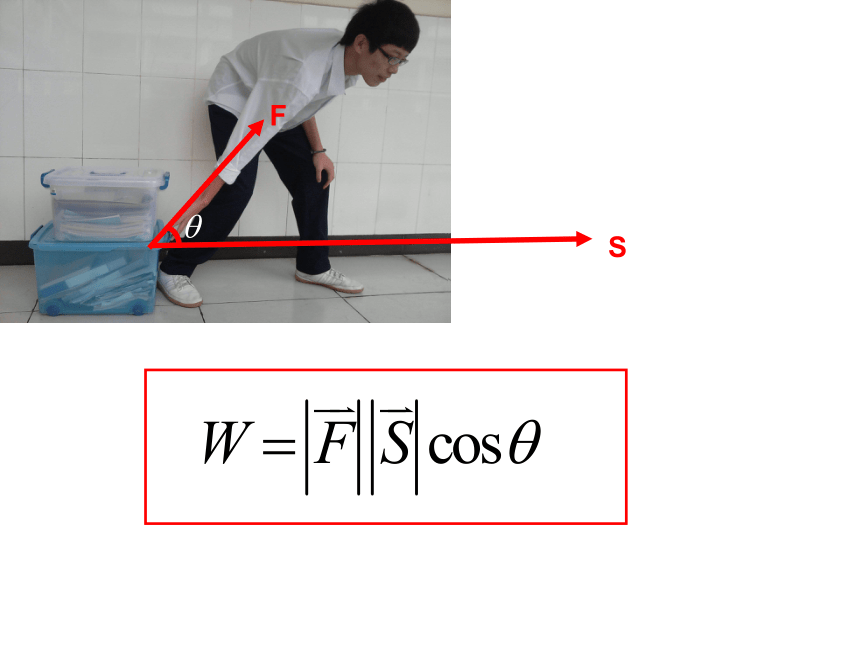
F
S
平面向量的数量积的定义
(2)数量积是一个实数
(3)公式可变形为 (可用来求夹角)
(4)零向量与任意向量的数量积都是0
(1) 之间的 不能省略,也不能改为
两个非零向量 的数量积(或内积)表示为:
投影: 叫做向量 在向量 方向上的投影
叫做向量 在向量 方向上的投影
的几何意义: 等于 与 在 的方向
上的投影 的乘积
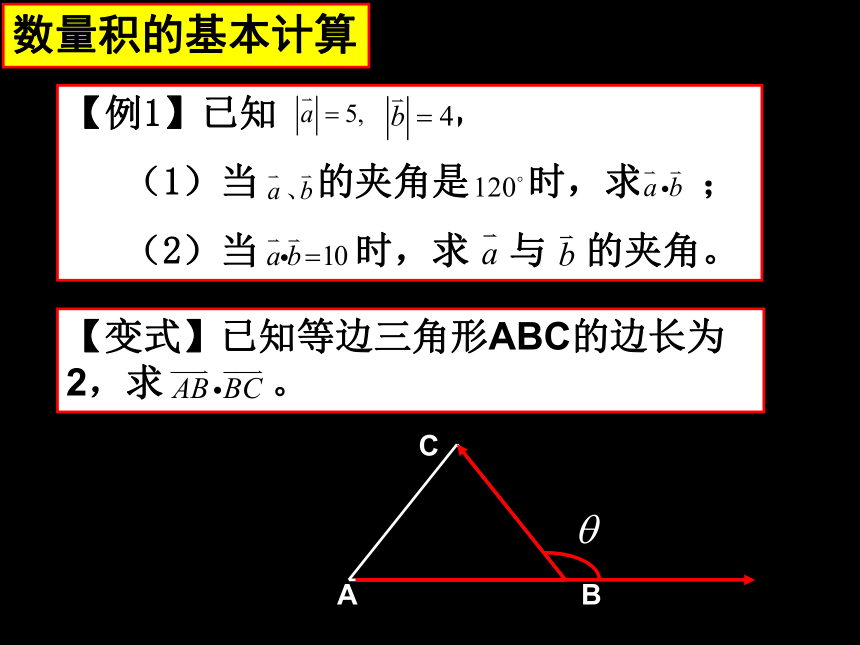
数量积的基本计算
【变式】已知等边三角形ABC的边长为 2,求 。
【例1】已知 ,
(1)当 的夹角是 时,求 ;
(2)当 时,求 与 的夹角。
A
B
C
1、
2、同向时,
反向时,
特别地,
或 (可用来求模)
3、 (重要不等式)
数量积的性质: 设 和 都是非零向量
·
·
·
·
·
O
M
【例2】判断下列结论是否正确。
(1)若 ,则对任意的 都有 ( √ )
(2)若 、 都为非零向量,则 ( )
(3)若 ,且 ,则 ( )
(4) 恒成立( )
性质的理解
(5)若 为不共线的非零向量,则 ( )
数量积的运算律
实数
向量
交换律
分配律
结合律
O
A
B
A’
B’
C
由图可知
则
即
所以
【例3】在实数的计算中经常用到下面三个乘法公式,那么对任意的向量 是否也有类似的结论成立?
实数 向量 说 明
知识迁移
可作
为公
式用
能力提升
【例4】已知 当 的夹角是
60°时,求 。
【变式】已知 当 的夹角
是60°时,求
【例5】已知 ,且 不共
线, 为何值时, 与 互相
垂直?
能力提升
六、小结、作业
作业:第108页 A组 第1、2、6、7
知识点小结:
①这节课我们利用物理中的“功”的概念得出向量的数量积的定义,进一步探究了数量积的性质及运算律;
②利用向量的数量积可以解决求向量的模的问题
( )和求向量的夹角( )
的问题,也可以解决平行、垂直问题。
2.4.1平面向量数量积的物理背景及其含义
湖南师大附中海口中学
瞿朝辉
F
S
平面向量的数量积的定义
(2)数量积是一个实数
(3)公式可变形为 (可用来求夹角)
(4)零向量与任意向量的数量积都是0
(1) 之间的 不能省略,也不能改为
两个非零向量 的数量积(或内积)表示为:
投影: 叫做向量 在向量 方向上的投影
叫做向量 在向量 方向上的投影
的几何意义: 等于 与 在 的方向
上的投影 的乘积
数量积的基本计算
【变式】已知等边三角形ABC的边长为 2,求 。
【例1】已知 ,
(1)当 的夹角是 时,求 ;
(2)当 时,求 与 的夹角。
A
B
C
1、
2、同向时,
反向时,
特别地,
或 (可用来求模)
3、 (重要不等式)
数量积的性质: 设 和 都是非零向量
·
·
·
·
·
O
M
【例2】判断下列结论是否正确。
(1)若 ,则对任意的 都有 ( √ )
(2)若 、 都为非零向量,则 ( )
(3)若 ,且 ,则 ( )
(4) 恒成立( )
性质的理解
(5)若 为不共线的非零向量,则 ( )
数量积的运算律
实数
向量
交换律
分配律
结合律
O
A
B
A’
B’
C
由图可知
则
即
所以
【例3】在实数的计算中经常用到下面三个乘法公式,那么对任意的向量 是否也有类似的结论成立?
实数 向量 说 明
知识迁移
可作
为公
式用
能力提升
【例4】已知 当 的夹角是
60°时,求 。
【变式】已知 当 的夹角
是60°时,求
【例5】已知 ,且 不共
线, 为何值时, 与 互相
垂直?
能力提升
六、小结、作业
作业:第108页 A组 第1、2、6、7
知识点小结:
①这节课我们利用物理中的“功”的概念得出向量的数量积的定义,进一步探究了数量积的性质及运算律;
②利用向量的数量积可以解决求向量的模的问题
( )和求向量的夹角( )
的问题,也可以解决平行、垂直问题。
