海口市2012年高中数学青年教师课堂教学评比材料:必修4. 2.4.1平面向量数量积的物理背景及其含义
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:必修4. 2.4.1平面向量数量积的物理背景及其含义 |  | |
| 格式 | zip | ||
| 文件大小 | 454.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 01:13:50 | ||
图片预览







文档简介
(共28张PPT)
林召高
前面我们已经研究了向量的线性运算,向量的线性运算包含哪些运算?这些运算的结果是什么量?
向量的线性运算包含向量的加法、减法和数乘向量运算,这些运算的结果都还是向量。
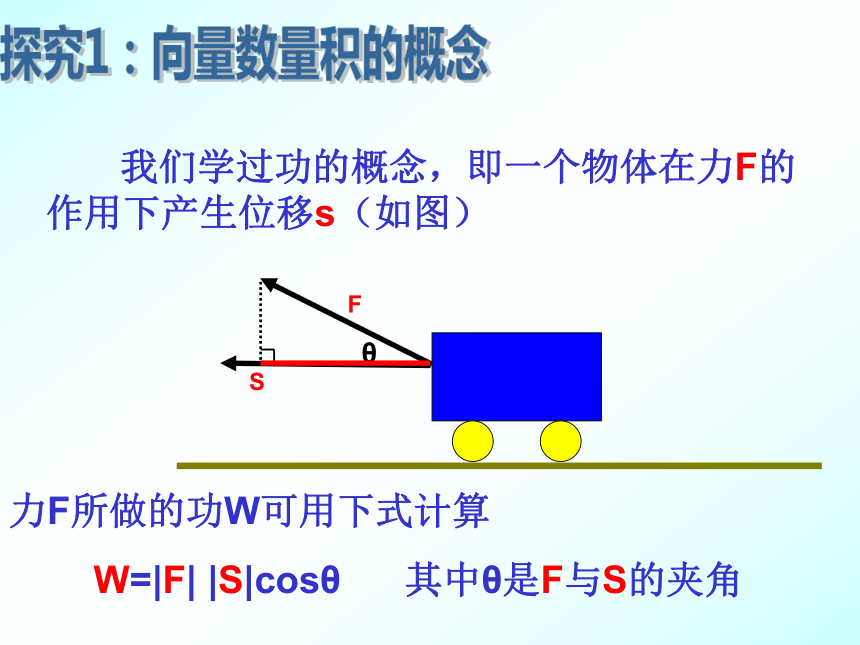
我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)
θ
F
S
力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角
向量数量积的定义
规定: .
(2)两向量的数量积是一个数量
(1) a · b不能写成a×b ,‘·’不能省
已知两个非零向量a 和b ,它们的夹角为 ,我们把数量 叫做a 与b 的数量积(或内积),记作a · b ,即
θ的范围 的结果
(正数,负数或者零)
00≤θ<900
θ=900
900<θ≤1800
根据向量数量积的定义,完成下列表格:
正数
零
负数
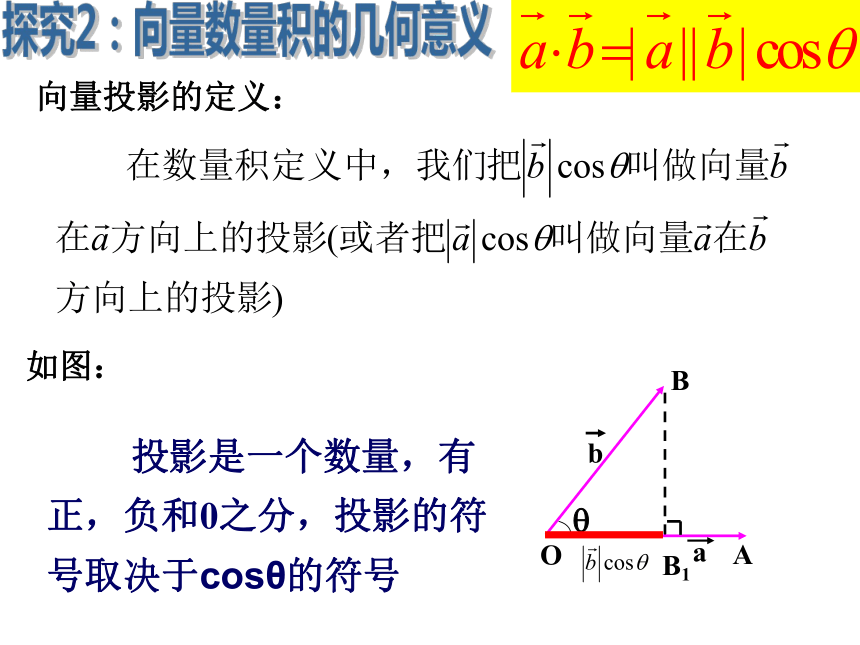
向量投影的定义:
如图:
B1
O
A
B
b
a
投影是一个数量,有正,负和0之分,投影的符号取决于cosθ的符号
数量积的几何意义:
向量投影的定义:
数量积 等于 的长度 与 在 的方向上的
投影 的乘积,或等于 的长度与 在 方向上的投影︱a︱cosθ的乘积。
④、
②、
①、
③、
①、
②、
解:
④、
②、
①、
③、
③、
④、
解:
(1)将例1中问题①②③的结论推广到一般向量,你能得到哪些结论?
(2)比较 的大小,你有什么结论?
④、
②、
①、
③、
数量积的性质:
设a,b都是非零向量,则:
特别地
√
×
×
×
1.若a =0,则对任一向量b ,有a · b=0.
2.若a ≠0,则对任一非零向量b ,有a · b≠0.
3.若a ≠0,a · b =0,则b=0
4.若b≠0,a · b= b · c,则a=c
练习:判断下列说法是否正确
在实数中
交换律: ab=ba
结合律: (ab)c=a(bc)
分配律: (a+b)c=ab+bc
回顾实数乘法运算中有关的运算律
( )
( )
( )
√
交换律:
结合律:
分配律:
( )
√
×
数量积的运算律
回顾实数乘法运算中的运算律,类比猜想数量积得运算律:
分析:
即证明:和的投影等于投影的和
证明:
数量积的运算律
回顾实数乘法运算中的运算律,类比猜想数量积得运算律:
( )
( )
( )
√
交换律:
结合律:
分配律:
( )
√
×
√
数量积的运算规律:
证明:(1)(a+b)2=(a+b)·(a+b)
=(a+b)·a+(a+b)·b
=a·a+b·a+a·b+b·b
证明:(2)(a+b)·(a-b)
=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
解:
1、课本第106页练习2、3
一、数量积的定义
二、数量积的几何意义
三、数量积的性质
特别地
四、数量积的运算规律
五、数量积的性质及
运算规律的应用
思考:用向量方法证明:直径所对的圆周角为直角。
A
B
C
O
如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°
分析:要证∠ACB=90°,只须证向
量 ,即 。
解:设
则 ,
由此可得:
即 ,∠ACB=90°
1、课本P108习题2.4A组1、2、3。
课后作业:
林召高
前面我们已经研究了向量的线性运算,向量的线性运算包含哪些运算?这些运算的结果是什么量?
向量的线性运算包含向量的加法、减法和数乘向量运算,这些运算的结果都还是向量。
我们学过功的概念,即一个物体在力F的作用下产生位移s(如图)
θ
F
S
力F所做的功W可用下式计算
W=|F| |S|cosθ 其中θ是F与S的夹角
向量数量积的定义
规定: .
(2)两向量的数量积是一个数量
(1) a · b不能写成a×b ,‘·’不能省
已知两个非零向量a 和b ,它们的夹角为 ,我们把数量 叫做a 与b 的数量积(或内积),记作a · b ,即
θ的范围 的结果
(正数,负数或者零)
00≤θ<900
θ=900
900<θ≤1800
根据向量数量积的定义,完成下列表格:
正数
零
负数
向量投影的定义:
如图:
B1
O
A
B
b
a
投影是一个数量,有正,负和0之分,投影的符号取决于cosθ的符号
数量积的几何意义:
向量投影的定义:
数量积 等于 的长度 与 在 的方向上的
投影 的乘积,或等于 的长度与 在 方向上的投影︱a︱cosθ的乘积。
④、
②、
①、
③、
①、
②、
解:
④、
②、
①、
③、
③、
④、
解:
(1)将例1中问题①②③的结论推广到一般向量,你能得到哪些结论?
(2)比较 的大小,你有什么结论?
④、
②、
①、
③、
数量积的性质:
设a,b都是非零向量,则:
特别地
√
×
×
×
1.若a =0,则对任一向量b ,有a · b=0.
2.若a ≠0,则对任一非零向量b ,有a · b≠0.
3.若a ≠0,a · b =0,则b=0
4.若b≠0,a · b= b · c,则a=c
练习:判断下列说法是否正确
在实数中
交换律: ab=ba
结合律: (ab)c=a(bc)
分配律: (a+b)c=ab+bc
回顾实数乘法运算中有关的运算律
( )
( )
( )
√
交换律:
结合律:
分配律:
( )
√
×
数量积的运算律
回顾实数乘法运算中的运算律,类比猜想数量积得运算律:
分析:
即证明:和的投影等于投影的和
证明:
数量积的运算律
回顾实数乘法运算中的运算律,类比猜想数量积得运算律:
( )
( )
( )
√
交换律:
结合律:
分配律:
( )
√
×
√
数量积的运算规律:
证明:(1)(a+b)2=(a+b)·(a+b)
=(a+b)·a+(a+b)·b
=a·a+b·a+a·b+b·b
证明:(2)(a+b)·(a-b)
=(a+b)·a-(a+b)·b
=a·a+b·a-a·b-b·b
解:
1、课本第106页练习2、3
一、数量积的定义
二、数量积的几何意义
三、数量积的性质
特别地
四、数量积的运算规律
五、数量积的性质及
运算规律的应用
思考:用向量方法证明:直径所对的圆周角为直角。
A
B
C
O
如图所示,已知⊙O,AB为直径,C
为⊙O上任意一点。求证∠ACB=90°
分析:要证∠ACB=90°,只须证向
量 ,即 。
解:设
则 ,
由此可得:
即 ,∠ACB=90°
1、课本P108习题2.4A组1、2、3。
课后作业:
