海口市2012年高中数学青年教师课堂教学评比材料:必修4. 2.3平面向量 基本定理及坐标表示(第一课时)课件
文档属性
| 名称 | 海口市2012年高中数学青年教师课堂教学评比材料:必修4. 2.3平面向量 基本定理及坐标表示(第一课时)课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 01:33:10 | ||
图片预览



文档简介
(共16张PPT)
2.3.1平面向量基本定理
琼山中学 李秋娇
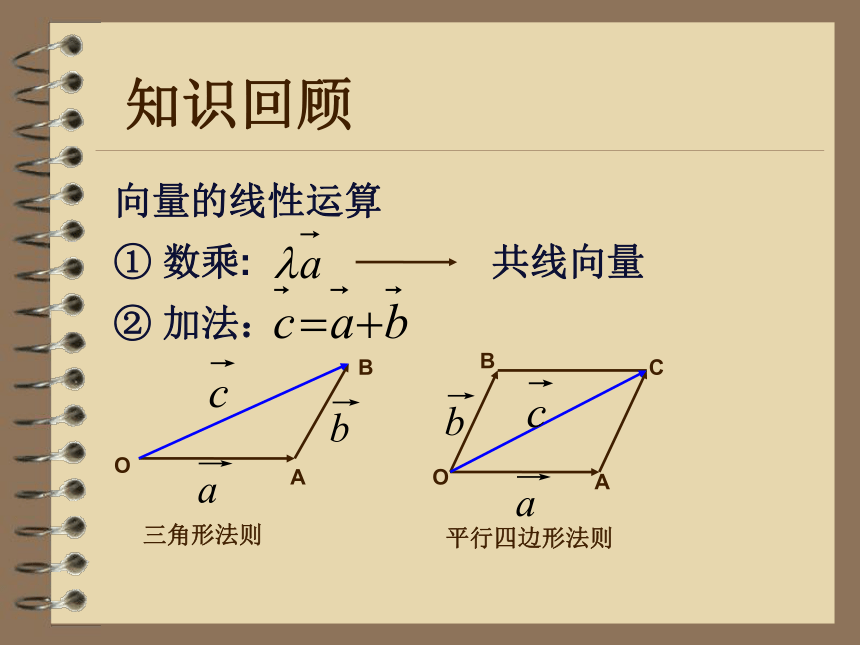
知识回顾
向量的线性运算
① 数乘:
② 加法:
共线向量
O
O
A
B
A
B
C
三角形法则
平行四边形法则
C
A
B
O
C
A
B
O
C
A
B
O
C
A
B
O
O
A
B
C
M
N
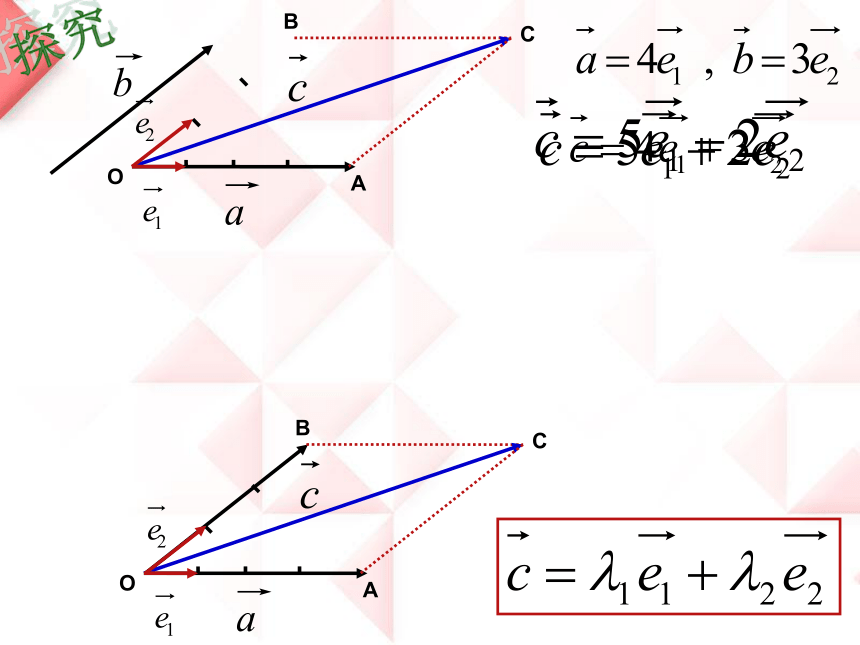
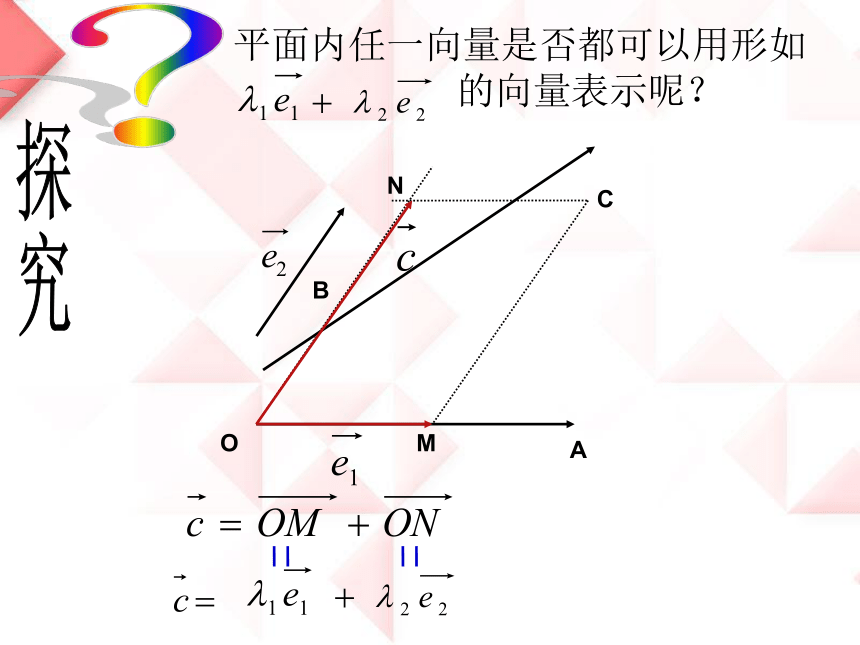
平面内任一向量是否都可以用形如
的向量表示呢?
如果 , 是同一平面内的两个不共线的
向量,那么对于这一平面内的任一向量 ,
有且只有一对实数 1、 2使
= 1 + 2
平面向量基本定理
其中不共线的向量 , 叫做表示这一
平面内的所有向量的一组基底。
如果 , 是同一平面内的两个不共线的
向量,那么对于这一平面内的任一向量 ,
有且只有一对实数 1、 2使
= 1 + 2
平面向量基本定理
其中不共线的向量 , 叫做表示这一
平面内的所有向量的一组基底。
.gsp
例题讲解
例1 已知向量e1,e2,求作向量-2.5e1+3e2 .
作法:(1)任取一点o,
作OA=-2.5e1,OB=3e2
e1
e2
O
C
-2.5e1
A
B
3e2
(2)作 OACB.
于是OC就是所求作的向量.
试一试
如图,已知向量 与 垂直,
请根据平面向量基本定理,用 , 表示 .
O
A
B
C
变式
例2设e1,e2是两个不共线向量, ,
,请根据平面向量基本定理,以 , 为
基底表示 .
解:根据平面向量基本定理,得
整理得,
解得,
例题讲解
设e1,e2是两个不共线向量,请根据平面向量基本定理, 以 , 为基底表示 .
(1) , ,
(2) , ,
变式训练
向量的夹角
如图,已知两个非零向量a和b,
则∠AOB=θ (0 °≤θ≤180°)
叫做a与b 的夹角
o
B
A
a
b
共起点
A
B
C
D
2
4
E
课堂小结:
2.向量的夹角:共起点的两个向量形成的角
如果 , 是同一平面内的两个不共线的向量,
那么对于这一平面内的任一向量 ,有且只有一对
实数 1、 2使 = 1 + 2
1.平面向量的基本定理
作业: 练习册第95页第2,3题
谢谢
琼山中学 李秋娇
2.3.1平面向量基本定理
琼山中学 李秋娇
知识回顾
向量的线性运算
① 数乘:
② 加法:
共线向量
O
O
A
B
A
B
C
三角形法则
平行四边形法则
C
A
B
O
C
A
B
O
C
A
B
O
C
A
B
O
O
A
B
C
M
N
平面内任一向量是否都可以用形如
的向量表示呢?
如果 , 是同一平面内的两个不共线的
向量,那么对于这一平面内的任一向量 ,
有且只有一对实数 1、 2使
= 1 + 2
平面向量基本定理
其中不共线的向量 , 叫做表示这一
平面内的所有向量的一组基底。
如果 , 是同一平面内的两个不共线的
向量,那么对于这一平面内的任一向量 ,
有且只有一对实数 1、 2使
= 1 + 2
平面向量基本定理
其中不共线的向量 , 叫做表示这一
平面内的所有向量的一组基底。
.gsp
例题讲解
例1 已知向量e1,e2,求作向量-2.5e1+3e2 .
作法:(1)任取一点o,
作OA=-2.5e1,OB=3e2
e1
e2
O
C
-2.5e1
A
B
3e2
(2)作 OACB.
于是OC就是所求作的向量.
试一试
如图,已知向量 与 垂直,
请根据平面向量基本定理,用 , 表示 .
O
A
B
C
变式
例2设e1,e2是两个不共线向量, ,
,请根据平面向量基本定理,以 , 为
基底表示 .
解:根据平面向量基本定理,得
整理得,
解得,
例题讲解
设e1,e2是两个不共线向量,请根据平面向量基本定理, 以 , 为基底表示 .
(1) , ,
(2) , ,
变式训练
向量的夹角
如图,已知两个非零向量a和b,
则∠AOB=θ (0 °≤θ≤180°)
叫做a与b 的夹角
o
B
A
a
b
共起点
A
B
C
D
2
4
E
课堂小结:
2.向量的夹角:共起点的两个向量形成的角
如果 , 是同一平面内的两个不共线的向量,
那么对于这一平面内的任一向量 ,有且只有一对
实数 1、 2使 = 1 + 2
1.平面向量的基本定理
作业: 练习册第95页第2,3题
谢谢
琼山中学 李秋娇
