人教版六年级上册5 圆练习十六、十七课件(31张PPT)
文档属性
| 名称 | 人教版六年级上册5 圆练习十六、十七课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 19:25:38 | ||
图片预览



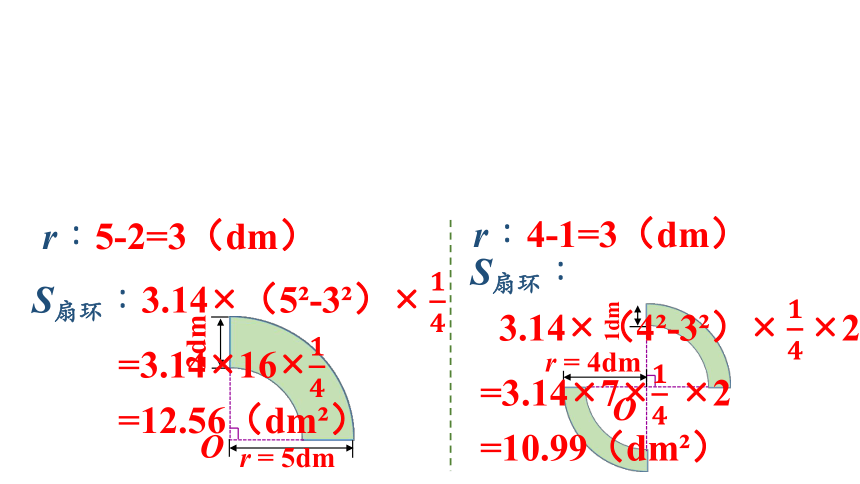



文档简介
(共31张PPT)
人教版数学
六年级上册
人教版数学六年级(上)
练习十六
圆
5
重点回顾
关于扇形你了解到哪些知识?
2.圆上两点之间的部分叫做弧。
1.一条弧和经过这条弧两端的两条半径所围
成的图形叫做扇形。
3.顶点在圆心的角叫做圆心角。
4.在同一个圆中,扇形的大小与这个扇形的
圆心角的大小有关。
练习巩固
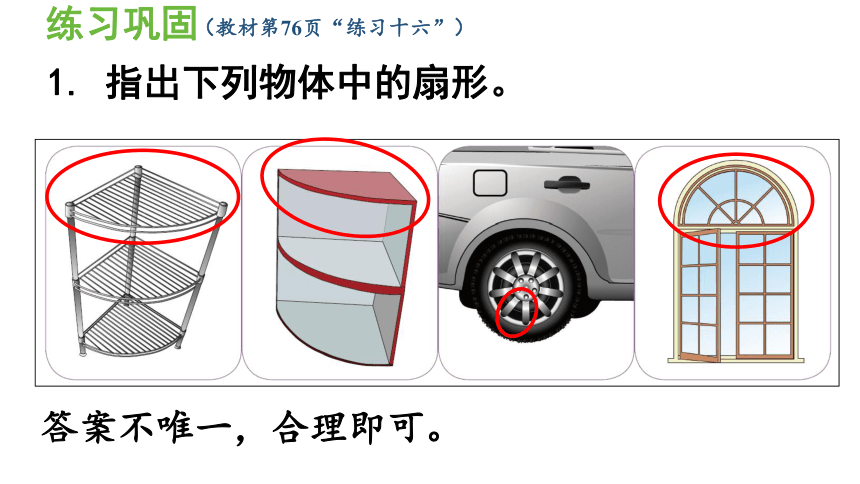
1. 指出下列物体中的扇形。
答案不唯一,合理即可。
(教材第76页“练习十六”)
( )
( )
( )
( )
√
O
O
A
B
B
A
O
B
A
O
A
B
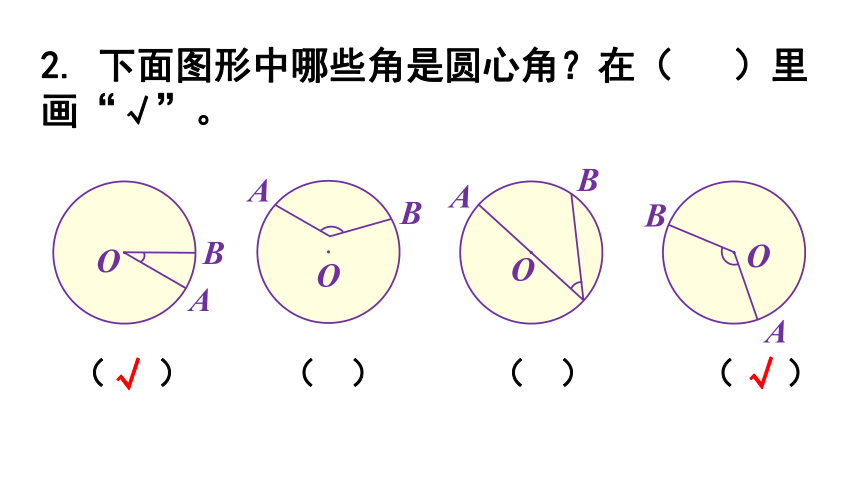
2. 下面图形中哪些角是圆心角?在( )里画“√”。
√
2cm
100°
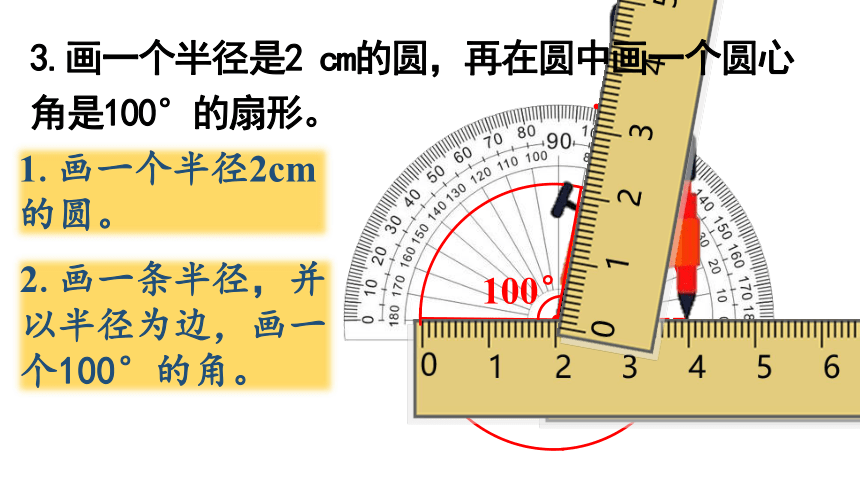
1.画一个半径2cm的圆。
2.画一条半径,并以半径为边,画一个100°的角。
3.画一个半径是2 cm的圆,再在圆中画一个圆心角是100°的扇形。
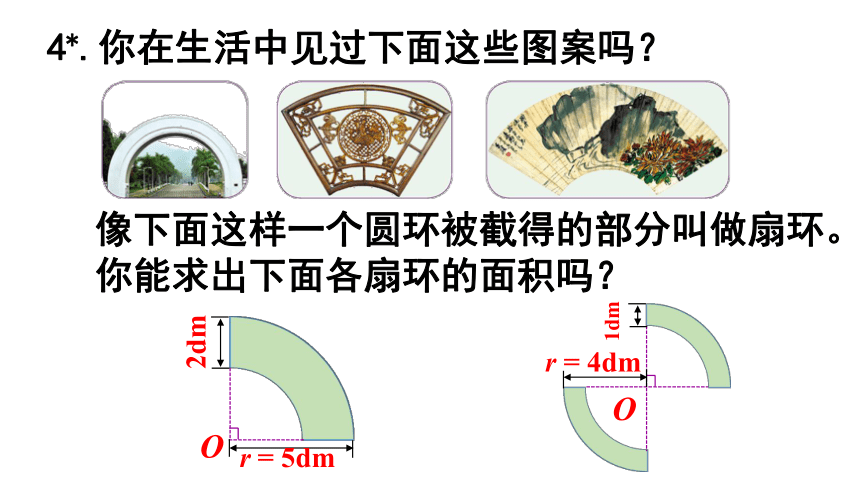
4*.你在生活中见过下面这些图案吗?
像下面这样一个圆环被截得的部分叫做扇环。你能求出下面各扇环的面积吗?
O
O
r = 5dm
r = 4dm
2dm
1dm
O
O
r = 5dm
r = 4dm
2dm
1dm
S扇环:3.14×(5 -3 )
=3.14×16×
=12.56(dm )
r:5-2=3(dm)
r:4-1=3(dm)
S扇环:
3.14×(4 -3 )
=3.14×7×
=10.99(dm )
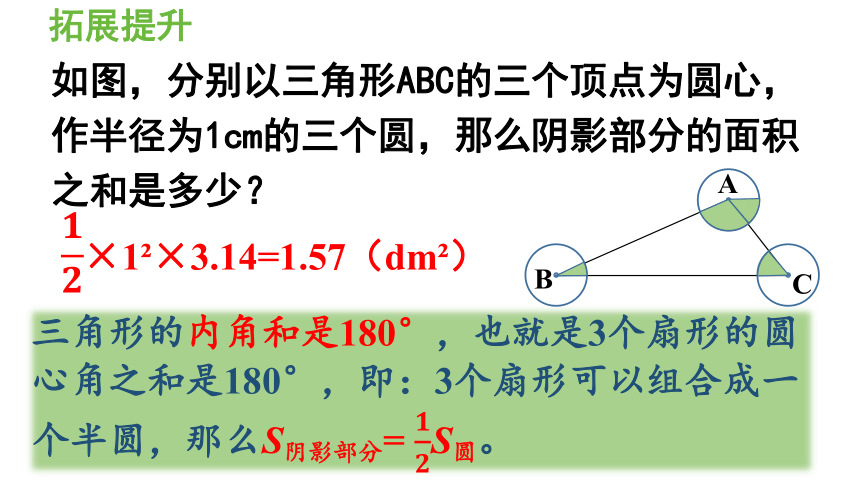
拓展提升
三角形的内角和是180°,也就是3个扇形的圆心角之和是180°,即:3个扇形可以组合成一个半圆,那么S阴影部分= S圆。
如图,分别以三角形ABC的三个顶点为圆心,作半径为1cm的三个圆,那么阴影部分的面积之和是多少?
×1 ×3.14=1.57(dm )
A
B
C
人教版数学六年级(上)
练习十七
圆
5
重点回顾
你学到了哪些关于圆的知识?
学习了圆的认识、圆的周长、圆的面积等相关知识。
圆的认识
画圆
实物画圆法、手指画圆法、系绳画圆法和圆规画圆法(定半径、定圆心、画圆)
圆的特征
圆是由曲线围成的封闭图形。
圆的各部分
圆心O:决定圆的位置
半径r :决定圆的大小
直径d :同圆或等圆中, d=2r或
有无数条
扇形
一条弧和经过这条弧两端的两条半径所围成的图形。
圆的周长
圆周率
一个圆的周长与它直径的比值叫做圆周率,它是一个固定值,是一个无限不循环小数,用字母π表示,计算时通常取3.14。
圆的周长计算公式
C=πd或C=2πr
圆的面积
圆环的面积计算公式
S=πR -πr 或S=π(R -r )
解决问题
外方内圆:正方形边长=圆的直径
外圆内方:正方形对角线=圆的直径
圆的面积
S=πr
练习巩固
(教材第78页“练习十七”)
1.你见过“驴拉磨”吗?如果驴绕着一个半径为1.2m的圆走一圈,大约要走多少米?
C=πd或C=2πr
2×3.14×1.2=7.536(m)
答:大约要走7.536米。
2.右图中的双面绣作品中间部分的画是一个直径是20cm的圆。这幅画的面积是多少?
S:3.14×102=314(cm2)
答:这幅画的面积是314cm2。
S=πr r=
r: 20÷2=10(cm)
3.用10m长的铁条做直径是50cm的圆形铁环,最多可以做多少个?
3.14×50=157(cm)
10÷1.57≈6(个)
答:最多可以做6个。
解题关键是求一个圆形铁环需要多长的铁条,即求圆的周长。
(去尾法保留整数)
157cm=1.57m
4.儿童乐园要修建一个圆形旋转木马场地,木马旋转范围的直径是8 m,周边还要留出1 m宽的小路,并在外侧围上栏杆,这块场地的占地面积是多少?
S=πr2
3.14×(8÷2+1)2
=3.14×25
=78.5(m2)
答:这块场地占地面积是78.5cm2。
木马旋转范围
d=8m
1m
5.一个羊圈依墙而建,呈半圆形,半径是5m。
(1)修这个羊圈需要多长的栅栏?
(2)如果要扩建这个羊圈,把它的直径增加2m。羊圈的面积增加了多少?
r=8m
r=8m
3.14×2×5÷2
=3.14×5×(2÷2)
=3.14×5
=15.7(m)
答:需要15.7m长的栅栏。
5.一个羊圈依墙而建,呈半圆形,半径是5m。
(1)修这个羊圈需要多长的栅栏?
栅栏的长相当于圆周长的一半。
5.一个羊圈依墙而建,呈半圆形,半径是5m。
(2)如果要扩建这个羊圈,把它的直径增加2m。羊圈的面积增加了多少?
r=8m
1m
1m
R:5+2÷2=6(m)
S:3.14×(62-52 )÷2 =17.27(m2)
答:羊圈的面积增加了17.27m 。
直径增加2m,也就是环宽2÷2=1m,羊圈增加的面积相当于半个圆环的面积。
6.判断对错,对的画“√”,错的画“×” 。
(1)圆周率π就是3.14。 ( )
(2)圆的半径扩大到原来的2倍,周长和面积也
扩大到原来的2倍。 ( )
(3)半径相等的两个圆周长相等。 ( )
√
×
×
π是一个无限不循环小数。
面积扩大到原来的4倍。
6.判断对错,对的画“√”,错的画“×” 。
(4)两个圆的直径相等,它们的半径也一定
相等。 ( )
(5)有4个圆心角都是90°的扇形,一定可以
拼成一个圆。 ( )
×
√
只有这4个扇形的半径都相等,才能拼成一个圆。
7.如图,一台压路机的前轮直径是1.7 m,如果前轮每分钟转动6周,压路机10分钟前进多远?
答:压路机10分钟前进320.28m。
10分钟:32.028×10=320.28(m)
前轮行进一周走的路程就是车轮周长。
C:3.14×1.7=5.338(m)
1分钟: 5.338×6=32.028(m)
半圆的周长=圆周长的一半+一条直径,C半圆=+2r 。
8.如图,街心公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?
r=25(m)
S:3.14×252 =196.25(m2)
答:总面积是196.25m2。
一个圆的面积
9.如图,中间是边长为1 cm的正方形,与这个正方形,每一条边相连的都是圆心角为90的扇形,整个图形的面积是多少?
r=1cm
a=1cm
3.14×12+1×1
=3.14×1+1
=3.14+1
=4.14(cm2)
答:整个图形的面积为4.14 cm2。
小晨跑一圈需要跑过两条弧线+两条正方形边长。
50m
10.如图,学校操场的跑道由正方形的两条对边和两个半圆组成。小晨在操场上跑了5圈,一共是多少米?
d=50m
5圈:257×5=1285(米)
答:一共是1285米。
两条弧线又可以组成一个d=50m的圆。
1圈:50×2+3.14×50=257(米)
拓展提升
1.把一张圆形纸片对折三次,对折后的图形及对应的曲线长度如图所示,那么圆形纸片的直径是多少?面积是多少?
1.57cm
如图将对折后的图形依次展开可看出,对折三次就是把圆平均分成8份,那么曲线的长度就是圆周长的。
C:1.57×8=12.56(cm)
d:12.56÷3.14=4(cm)
S:(4÷2) ×3.14=12.56(cm )
答:圆形纸片的直径是4cm,面积为12.56 cm2。
2.长方形的面积是36 cm ,求阴影部分的面积。(单位:cm)
长:36÷4=9(cm)
A是一个扇形,是一个半径为4cm的圆。
4
A
B
B可以看做是底为4cm,高是9-4=5(cm)的三角形。
A面积:×3.14×4 =12.56(cm )
B面积:4×(9-4)÷2=10(cm )
阴影面积:36-12.56-10=13.44(cm )
人教版数学
六年级上册
人教版数学六年级(上)
练习十六
圆
5
重点回顾
关于扇形你了解到哪些知识?
2.圆上两点之间的部分叫做弧。
1.一条弧和经过这条弧两端的两条半径所围
成的图形叫做扇形。
3.顶点在圆心的角叫做圆心角。
4.在同一个圆中,扇形的大小与这个扇形的
圆心角的大小有关。
练习巩固
1. 指出下列物体中的扇形。
答案不唯一,合理即可。
(教材第76页“练习十六”)
( )
( )
( )
( )
√
O
O
A
B
B
A
O
B
A
O
A
B
2. 下面图形中哪些角是圆心角?在( )里画“√”。
√
2cm
100°
1.画一个半径2cm的圆。
2.画一条半径,并以半径为边,画一个100°的角。
3.画一个半径是2 cm的圆,再在圆中画一个圆心角是100°的扇形。
4*.你在生活中见过下面这些图案吗?
像下面这样一个圆环被截得的部分叫做扇环。你能求出下面各扇环的面积吗?
O
O
r = 5dm
r = 4dm
2dm
1dm
O
O
r = 5dm
r = 4dm
2dm
1dm
S扇环:3.14×(5 -3 )
=3.14×16×
=12.56(dm )
r:5-2=3(dm)
r:4-1=3(dm)
S扇环:
3.14×(4 -3 )
=3.14×7×
=10.99(dm )
拓展提升
三角形的内角和是180°,也就是3个扇形的圆心角之和是180°,即:3个扇形可以组合成一个半圆,那么S阴影部分= S圆。
如图,分别以三角形ABC的三个顶点为圆心,作半径为1cm的三个圆,那么阴影部分的面积之和是多少?
×1 ×3.14=1.57(dm )
A
B
C
人教版数学六年级(上)
练习十七
圆
5
重点回顾
你学到了哪些关于圆的知识?
学习了圆的认识、圆的周长、圆的面积等相关知识。
圆的认识
画圆
实物画圆法、手指画圆法、系绳画圆法和圆规画圆法(定半径、定圆心、画圆)
圆的特征
圆是由曲线围成的封闭图形。
圆的各部分
圆心O:决定圆的位置
半径r :决定圆的大小
直径d :同圆或等圆中, d=2r或
有无数条
扇形
一条弧和经过这条弧两端的两条半径所围成的图形。
圆的周长
圆周率
一个圆的周长与它直径的比值叫做圆周率,它是一个固定值,是一个无限不循环小数,用字母π表示,计算时通常取3.14。
圆的周长计算公式
C=πd或C=2πr
圆的面积
圆环的面积计算公式
S=πR -πr 或S=π(R -r )
解决问题
外方内圆:正方形边长=圆的直径
外圆内方:正方形对角线=圆的直径
圆的面积
S=πr
练习巩固
(教材第78页“练习十七”)
1.你见过“驴拉磨”吗?如果驴绕着一个半径为1.2m的圆走一圈,大约要走多少米?
C=πd或C=2πr
2×3.14×1.2=7.536(m)
答:大约要走7.536米。
2.右图中的双面绣作品中间部分的画是一个直径是20cm的圆。这幅画的面积是多少?
S:3.14×102=314(cm2)
答:这幅画的面积是314cm2。
S=πr r=
r: 20÷2=10(cm)
3.用10m长的铁条做直径是50cm的圆形铁环,最多可以做多少个?
3.14×50=157(cm)
10÷1.57≈6(个)
答:最多可以做6个。
解题关键是求一个圆形铁环需要多长的铁条,即求圆的周长。
(去尾法保留整数)
157cm=1.57m
4.儿童乐园要修建一个圆形旋转木马场地,木马旋转范围的直径是8 m,周边还要留出1 m宽的小路,并在外侧围上栏杆,这块场地的占地面积是多少?
S=πr2
3.14×(8÷2+1)2
=3.14×25
=78.5(m2)
答:这块场地占地面积是78.5cm2。
木马旋转范围
d=8m
1m
5.一个羊圈依墙而建,呈半圆形,半径是5m。
(1)修这个羊圈需要多长的栅栏?
(2)如果要扩建这个羊圈,把它的直径增加2m。羊圈的面积增加了多少?
r=8m
r=8m
3.14×2×5÷2
=3.14×5×(2÷2)
=3.14×5
=15.7(m)
答:需要15.7m长的栅栏。
5.一个羊圈依墙而建,呈半圆形,半径是5m。
(1)修这个羊圈需要多长的栅栏?
栅栏的长相当于圆周长的一半。
5.一个羊圈依墙而建,呈半圆形,半径是5m。
(2)如果要扩建这个羊圈,把它的直径增加2m。羊圈的面积增加了多少?
r=8m
1m
1m
R:5+2÷2=6(m)
S:3.14×(62-52 )÷2 =17.27(m2)
答:羊圈的面积增加了17.27m 。
直径增加2m,也就是环宽2÷2=1m,羊圈增加的面积相当于半个圆环的面积。
6.判断对错,对的画“√”,错的画“×” 。
(1)圆周率π就是3.14。 ( )
(2)圆的半径扩大到原来的2倍,周长和面积也
扩大到原来的2倍。 ( )
(3)半径相等的两个圆周长相等。 ( )
√
×
×
π是一个无限不循环小数。
面积扩大到原来的4倍。
6.判断对错,对的画“√”,错的画“×” 。
(4)两个圆的直径相等,它们的半径也一定
相等。 ( )
(5)有4个圆心角都是90°的扇形,一定可以
拼成一个圆。 ( )
×
√
只有这4个扇形的半径都相等,才能拼成一个圆。
7.如图,一台压路机的前轮直径是1.7 m,如果前轮每分钟转动6周,压路机10分钟前进多远?
答:压路机10分钟前进320.28m。
10分钟:32.028×10=320.28(m)
前轮行进一周走的路程就是车轮周长。
C:3.14×1.7=5.338(m)
1分钟: 5.338×6=32.028(m)
半圆的周长=圆周长的一半+一条直径,C半圆=+2r 。
8.如图,街心公园有两块半圆形的草坪,它们的周长都是128.5 m,这两块草坪的总面积是多少?
r=25(m)
S:3.14×252 =196.25(m2)
答:总面积是196.25m2。
一个圆的面积
9.如图,中间是边长为1 cm的正方形,与这个正方形,每一条边相连的都是圆心角为90的扇形,整个图形的面积是多少?
r=1cm
a=1cm
3.14×12+1×1
=3.14×1+1
=3.14+1
=4.14(cm2)
答:整个图形的面积为4.14 cm2。
小晨跑一圈需要跑过两条弧线+两条正方形边长。
50m
10.如图,学校操场的跑道由正方形的两条对边和两个半圆组成。小晨在操场上跑了5圈,一共是多少米?
d=50m
5圈:257×5=1285(米)
答:一共是1285米。
两条弧线又可以组成一个d=50m的圆。
1圈:50×2+3.14×50=257(米)
拓展提升
1.把一张圆形纸片对折三次,对折后的图形及对应的曲线长度如图所示,那么圆形纸片的直径是多少?面积是多少?
1.57cm
如图将对折后的图形依次展开可看出,对折三次就是把圆平均分成8份,那么曲线的长度就是圆周长的。
C:1.57×8=12.56(cm)
d:12.56÷3.14=4(cm)
S:(4÷2) ×3.14=12.56(cm )
答:圆形纸片的直径是4cm,面积为12.56 cm2。
2.长方形的面积是36 cm ,求阴影部分的面积。(单位:cm)
长:36÷4=9(cm)
A是一个扇形,是一个半径为4cm的圆。
4
A
B
B可以看做是底为4cm,高是9-4=5(cm)的三角形。
A面积:×3.14×4 =12.56(cm )
B面积:4×(9-4)÷2=10(cm )
阴影面积:36-12.56-10=13.44(cm )
