(人教新课标)一年级数学下册8.2稍复杂的图形变化规律教案及练习题
文档属性
| 名称 | (人教新课标)一年级数学下册8.2稍复杂的图形变化规律教案及练习题 |  | |
| 格式 | zip | ||
| 文件大小 | 285.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 14:25:54 | ||
图片预览



文档简介
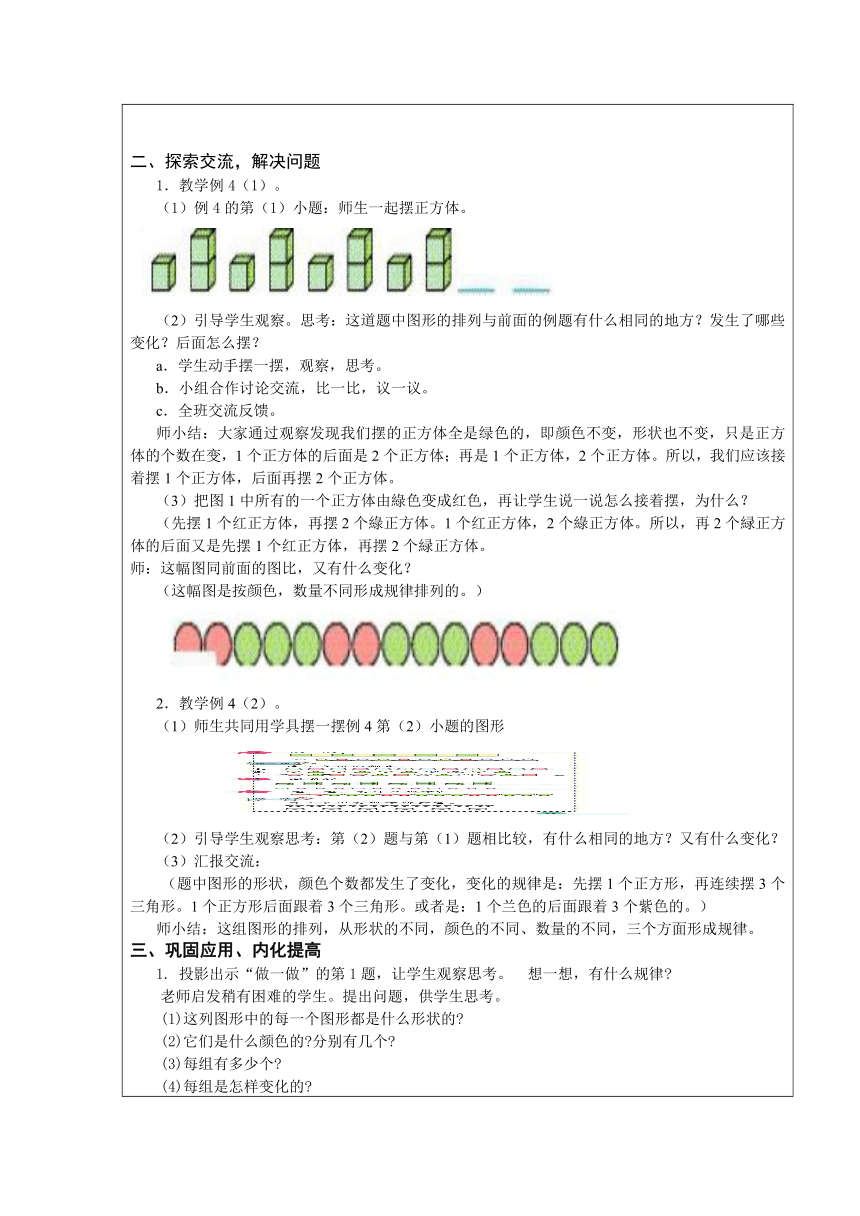
1.8.2稍复杂的图形变化规律
课 型 新授课 学 校 使用教师:
主备人 孙宝菊 修改人 孙晶 时 间
教学内容:稍复杂的图形变化规律。教材第89页例4,“做一做”及练习十六第2题。
教学目标:1.通过观察、比较,发现稍复杂的图形变化规律。 2.培养学生独立发现规律、创造规律的能力。 3.对学生进行数学美的教育。
重点、难点:1.引导学生发现稍复杂的图形变化规律。 2.引导学生创造规律。
教学准备:教学挂图,视频仪,学具卡片。
教 学 过 程
一、创设情境,生成问题师:上一节课,我们欣赏了一些美丽的图案,发现它们都是由一组图形依次不断地重复出现而形成的,也就是说,它们是有规律的排列。现在老师带来了几组图形,你能找出他们排列的规律吗?(一)我会在合适的图形上面打“√”。 (二)我能涂出有规律的颜色。生独立做,然后全班交流。师:看来小朋友们对上节课学习的找规律,掌握的不错。今天,我们继续研究图形的变化规律。(揭示课题)。二、探索交流,解决问题1.教学例4(1)。(1)例4的第(1)小题:师生一起摆正方体。 (2)引导学生观察。思考:这道题中图形的排列与前面的例题有什么相同的地方?发生了哪些变化?后面怎么摆?a.学生动手摆一摆,观察,思考。b.小组合作讨论交流,比一比,议一议。c.全班交流反馈。师小结:大家通过观察发现我们摆的正方体全是绿色的,即颜色不变,形状也不变,只是正方体的个数在变,1个正方体的后面是2个正方体;再是1个正方体,2个正方体。所以,我们应该接着摆1个正方体,后面再摆2个正方体。(3)把图1中所有的一个正方体由綠色变成红色,再让学生说一说怎么接着摆,为什么?(先摆1个红正方体,再摆2个綠正方体。1个红正方体,2个綠正方体。所以,再2个緑正方体的后面又是先摆1个红正方体,再摆2个緑正方体。师:这幅图同前面的图比,又有什么变化?(这幅图是按颜色,数量不同形成规律排列的。)2.教学例4(2)。(1)师生共同用学具摆一摆例4第(2)小题的图形 (2)引导学生观察思考:第(2)题与第(1)题相比较,有什么相同的地方?又有什么变化?(3)汇报交流:(题中图形的形状,颜色个数都发生了变化,变化的规律是:先摆1个正方形,再连续摆3个三角形。1个正方形后面跟着3个三角形。或者是:1个兰色的后面跟着3个紫色的。)师小结:这组图形的排列,从形状的不同,颜色的不同、数量的不同,三个方面形成规律。三、巩固应用、内化提高1. 投影出示“做一做”的第1题,让学生观察思考。 想一想,有什么规律 老师启发稍有困难的学生。提出问题,供学生思考。 (1)这列图形中的每一个图形都是什么形状的 (2)它们是什么颜色的 分别有几个 (3)每组有多少个 (4)每组是怎样变化的 (这列图形都是圆形的,有红色的也有绿色的。每组有5个,每组中有2个红色的圆形,3个绿色的圆形。每组都是2个红色圆形接着3个绿色的圆形这样变化的。) 2.投影出示“做一做”的第2题。自己涂出有规律的颜色。 鼓励学生大胆发挥想像力,只要涂出的颜色是有规律的或自己的解释是有道理的,就应该给予肯定和表扬。 对于设计新颖美观的画面,投影展示。 四、回顾整理,反思提升通过本节课的学习,你有什么收获?评价一下自己的表现。板书设计:稍复杂的图形变化规律
作业设计:
1.我会涂色。 2.我会摆。 3.我会接着画。
教学反思:
4.8.1 植树问题(一)
课 型 新 授 使用人
主备人 于守义 修改人 郭 婷
教学内容:人教版义务教育课程标准实验教科书四年级下册第八单元,教材第117 页的例1及第118页“做一做”。
教学目标: 1.使学生理解并掌握“植树问题”的基本解题方法,并能解决一些实际生活中存在的与“植树”有关的问题。2.掌握“植树问题”的第一种情况是“两端都要种”。3.培养学生认真审题的好习惯。
重点、难点:1.教学重点:掌握“两端都要种的植树问题”的解题方法。
2.教学难点:掌握已知株距和全长求株数的方法,以及已知株数和株距求全长的方法。
教学准备: 教学挂图(或小黑板)
教 学 过 程
一、创设情境,生成问题 1.猜谜:两棵小树十个杈,不长叶子不开花,能写会算还会画,天天干活不说话。生:手,或手指。 2.师:伸出左手,每两个手指间夹一枝笔,看看能夹多少枝笔。(笔不够用的可以用其他物品代替) 师:同学们考虑一下,手指的个数与夹住铅笔的枝数有什么关系呢?你能用数量关系表示出手指和间隔数的关系吗?(引导学生思考,引入“间隔数”。指名学生回答,教师相机板书:手指数=间隔数+1) 师:有的人患有多指症,如果他有6个手指,那么可以夹住几枝铅笔?为什么?(5枝,因为六个手指间有5个间隔)师:如果科学家们要制造出一个一支手能抓10枝笔的机器人,这个机器人一支手需要有几个手指头?(11个,因为11个手指头间才能有10个间隔) 3.师:其实在数学中也有许多类似手指问题一样的数学问题。我们称之为“植树问题”。(板书课题:植树问题)二、探索交流,解决问题 1.出示例1 为创建绿色园林城市,学校在100米长的主道一边植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗? 师:大家想一想、画一画、算一算“可能会种几棵?”再用自己喜欢的方式来说明。(学生独立思考,尝试说明。教师巡视,了解学生的书写情况,并及时指导) 2.互动交流 (1)小组交流师:同学们想的怎么样了,请把你的种植方法和同桌说一说。(学生互动交流,在小组内展示自己的种植方法,小组内互相订正) (2)组织全班交流 教师组织各小组推举代表汇报各组方法,并解释其想法。 (3)实践操作,发现规律① 引导学生思考:(课件或小黑板出示)大家看,在一段直路上种树,如果两端都种,种树的棵数与树之间的间隔数之间你发现了什么? (学生会很快发现:植树的棵数比间隔数多1) 师:是的,你们发现的很对。如果把这个发现用一个关系式来表示该怎样写呢?就是怎么得到棵数?生:植树的棵数=间隔数+1。 生:间隔数=棵数-1。(板书:棵数=间隔数+1 间隔数=棵数-1)② 提问:如果一排共有10棵树,中间会有几个间隔?1000棵树呢?如果一排树中间有10个间隔,你知道一共有多少棵树?100个间隔?如果分成n个间隔呢?(生:n+1=棵数)③ 师:这是学校的植树方案,这个线段图能看懂吗?请你帮助计算一下,小路的一侧共需要多少棵树? 如果有学生只说100÷5=20棵,提问:这个20表示什么?(20个间隔)(板书:100÷5+1=21棵) 师:如果每隔4米种一棵,共需要多少棵树?(100÷4+1=6棵)3.共同优化,形成结论(1)师:通过研究这道题,要求共种多少棵树,怎样计算? (可多指出几名学生回答,互相补充,形成结论。)(2)小结:求在一侧植树的棵数(两端都要植)用路长除以间距再加1。用公式表示是:路长÷间隔+1=棵数。三、巩固应用,内化提高师:与植树问题相类似的生活问题在身边还有很多,我们一起去看看。 1.学校要在100米长的主道路的一侧安装路灯(两端都安装),每隔20米安装一盏,一共需要安装多少盏路灯? 师:当题意难以理解时,可以画成线段图来理解,想一想,怎样列式计算?这个安装路灯的问题和刚才学过的植树问题有那些联系?2.为庆祝六一儿童节,学校要在长72米长的走廊上摆放鲜花,如果每3米放一盆(两端都要放),需要放多少盆花?如果每8米放一盆呢?3.在长10米的舞台前悬挂汽球进行装饰,每隔1米挂一个红汽球,每两个红汽球中挂一个黄汽球,已知两端都要挂红汽球。共需要多少红汽球,多少个黄汽球?*4.科学家进行一项实验,每隔5小时做一次记录,做第12次记录时,挂钟时针指向9。问:第一次记录时,时针指向几?四、回顾整理,反思提升师:通过这节课的学习你有什么收获? 板书设计: 植树问题 棵数=间隔数+1 间隔数=棵数-1 100÷5+1=21棵
作 业 设 计
基础:1.填一填。(1)下面的线段有( )个点,共有( )小段,不封闭图形的点数和段数的关系是( )。 (2)在一条长300米的公路两边种树,每隔4米种1棵(两端都要种),这样一共要种( )棵。 (3)如下图,在一条防风带上每隔30米种1棵树,这条防风带共种( )棵树,由此可以推断出两端都种树时,树的棵树比间隔数( )。综合:2.选一选:(1)一个圆形花坛的周长是36米,每隔4米摆一盆花,一共需要( )盆花。 A.8 B.9 C.10 D.11(2)一座楼房每上一层要16个台阶,小红每天回家要走80个台阶,小红家住( )楼。 A.5 B.6 C.7 D.8拓展提升:3.一条走廊长24米,每隔3米放一盆花,走廊两端都要放。一共要放多少盆花?
教学反思:
20m
5m
20m
5m
● ● ● ● ● ● ●
1500米
……
课 型 新授课 学 校 使用教师:
主备人 孙宝菊 修改人 孙晶 时 间
教学内容:稍复杂的图形变化规律。教材第89页例4,“做一做”及练习十六第2题。
教学目标:1.通过观察、比较,发现稍复杂的图形变化规律。 2.培养学生独立发现规律、创造规律的能力。 3.对学生进行数学美的教育。
重点、难点:1.引导学生发现稍复杂的图形变化规律。 2.引导学生创造规律。
教学准备:教学挂图,视频仪,学具卡片。
教 学 过 程
一、创设情境,生成问题师:上一节课,我们欣赏了一些美丽的图案,发现它们都是由一组图形依次不断地重复出现而形成的,也就是说,它们是有规律的排列。现在老师带来了几组图形,你能找出他们排列的规律吗?(一)我会在合适的图形上面打“√”。 (二)我能涂出有规律的颜色。生独立做,然后全班交流。师:看来小朋友们对上节课学习的找规律,掌握的不错。今天,我们继续研究图形的变化规律。(揭示课题)。二、探索交流,解决问题1.教学例4(1)。(1)例4的第(1)小题:师生一起摆正方体。 (2)引导学生观察。思考:这道题中图形的排列与前面的例题有什么相同的地方?发生了哪些变化?后面怎么摆?a.学生动手摆一摆,观察,思考。b.小组合作讨论交流,比一比,议一议。c.全班交流反馈。师小结:大家通过观察发现我们摆的正方体全是绿色的,即颜色不变,形状也不变,只是正方体的个数在变,1个正方体的后面是2个正方体;再是1个正方体,2个正方体。所以,我们应该接着摆1个正方体,后面再摆2个正方体。(3)把图1中所有的一个正方体由綠色变成红色,再让学生说一说怎么接着摆,为什么?(先摆1个红正方体,再摆2个綠正方体。1个红正方体,2个綠正方体。所以,再2个緑正方体的后面又是先摆1个红正方体,再摆2个緑正方体。师:这幅图同前面的图比,又有什么变化?(这幅图是按颜色,数量不同形成规律排列的。)2.教学例4(2)。(1)师生共同用学具摆一摆例4第(2)小题的图形 (2)引导学生观察思考:第(2)题与第(1)题相比较,有什么相同的地方?又有什么变化?(3)汇报交流:(题中图形的形状,颜色个数都发生了变化,变化的规律是:先摆1个正方形,再连续摆3个三角形。1个正方形后面跟着3个三角形。或者是:1个兰色的后面跟着3个紫色的。)师小结:这组图形的排列,从形状的不同,颜色的不同、数量的不同,三个方面形成规律。三、巩固应用、内化提高1. 投影出示“做一做”的第1题,让学生观察思考。 想一想,有什么规律 老师启发稍有困难的学生。提出问题,供学生思考。 (1)这列图形中的每一个图形都是什么形状的 (2)它们是什么颜色的 分别有几个 (3)每组有多少个 (4)每组是怎样变化的 (这列图形都是圆形的,有红色的也有绿色的。每组有5个,每组中有2个红色的圆形,3个绿色的圆形。每组都是2个红色圆形接着3个绿色的圆形这样变化的。) 2.投影出示“做一做”的第2题。自己涂出有规律的颜色。 鼓励学生大胆发挥想像力,只要涂出的颜色是有规律的或自己的解释是有道理的,就应该给予肯定和表扬。 对于设计新颖美观的画面,投影展示。 四、回顾整理,反思提升通过本节课的学习,你有什么收获?评价一下自己的表现。板书设计:稍复杂的图形变化规律
作业设计:
1.我会涂色。 2.我会摆。 3.我会接着画。
教学反思:
4.8.1 植树问题(一)
课 型 新 授 使用人
主备人 于守义 修改人 郭 婷
教学内容:人教版义务教育课程标准实验教科书四年级下册第八单元,教材第117 页的例1及第118页“做一做”。
教学目标: 1.使学生理解并掌握“植树问题”的基本解题方法,并能解决一些实际生活中存在的与“植树”有关的问题。2.掌握“植树问题”的第一种情况是“两端都要种”。3.培养学生认真审题的好习惯。
重点、难点:1.教学重点:掌握“两端都要种的植树问题”的解题方法。
2.教学难点:掌握已知株距和全长求株数的方法,以及已知株数和株距求全长的方法。
教学准备: 教学挂图(或小黑板)
教 学 过 程
一、创设情境,生成问题 1.猜谜:两棵小树十个杈,不长叶子不开花,能写会算还会画,天天干活不说话。生:手,或手指。 2.师:伸出左手,每两个手指间夹一枝笔,看看能夹多少枝笔。(笔不够用的可以用其他物品代替) 师:同学们考虑一下,手指的个数与夹住铅笔的枝数有什么关系呢?你能用数量关系表示出手指和间隔数的关系吗?(引导学生思考,引入“间隔数”。指名学生回答,教师相机板书:手指数=间隔数+1) 师:有的人患有多指症,如果他有6个手指,那么可以夹住几枝铅笔?为什么?(5枝,因为六个手指间有5个间隔)师:如果科学家们要制造出一个一支手能抓10枝笔的机器人,这个机器人一支手需要有几个手指头?(11个,因为11个手指头间才能有10个间隔) 3.师:其实在数学中也有许多类似手指问题一样的数学问题。我们称之为“植树问题”。(板书课题:植树问题)二、探索交流,解决问题 1.出示例1 为创建绿色园林城市,学校在100米长的主道一边植树,每隔5米栽一棵(两端要栽)。一共需要多少棵树苗? 师:大家想一想、画一画、算一算“可能会种几棵?”再用自己喜欢的方式来说明。(学生独立思考,尝试说明。教师巡视,了解学生的书写情况,并及时指导) 2.互动交流 (1)小组交流师:同学们想的怎么样了,请把你的种植方法和同桌说一说。(学生互动交流,在小组内展示自己的种植方法,小组内互相订正) (2)组织全班交流 教师组织各小组推举代表汇报各组方法,并解释其想法。 (3)实践操作,发现规律① 引导学生思考:(课件或小黑板出示)大家看,在一段直路上种树,如果两端都种,种树的棵数与树之间的间隔数之间你发现了什么? (学生会很快发现:植树的棵数比间隔数多1) 师:是的,你们发现的很对。如果把这个发现用一个关系式来表示该怎样写呢?就是怎么得到棵数?生:植树的棵数=间隔数+1。 生:间隔数=棵数-1。(板书:棵数=间隔数+1 间隔数=棵数-1)② 提问:如果一排共有10棵树,中间会有几个间隔?1000棵树呢?如果一排树中间有10个间隔,你知道一共有多少棵树?100个间隔?如果分成n个间隔呢?(生:n+1=棵数)③ 师:这是学校的植树方案,这个线段图能看懂吗?请你帮助计算一下,小路的一侧共需要多少棵树? 如果有学生只说100÷5=20棵,提问:这个20表示什么?(20个间隔)(板书:100÷5+1=21棵) 师:如果每隔4米种一棵,共需要多少棵树?(100÷4+1=6棵)3.共同优化,形成结论(1)师:通过研究这道题,要求共种多少棵树,怎样计算? (可多指出几名学生回答,互相补充,形成结论。)(2)小结:求在一侧植树的棵数(两端都要植)用路长除以间距再加1。用公式表示是:路长÷间隔+1=棵数。三、巩固应用,内化提高师:与植树问题相类似的生活问题在身边还有很多,我们一起去看看。 1.学校要在100米长的主道路的一侧安装路灯(两端都安装),每隔20米安装一盏,一共需要安装多少盏路灯? 师:当题意难以理解时,可以画成线段图来理解,想一想,怎样列式计算?这个安装路灯的问题和刚才学过的植树问题有那些联系?2.为庆祝六一儿童节,学校要在长72米长的走廊上摆放鲜花,如果每3米放一盆(两端都要放),需要放多少盆花?如果每8米放一盆呢?3.在长10米的舞台前悬挂汽球进行装饰,每隔1米挂一个红汽球,每两个红汽球中挂一个黄汽球,已知两端都要挂红汽球。共需要多少红汽球,多少个黄汽球?*4.科学家进行一项实验,每隔5小时做一次记录,做第12次记录时,挂钟时针指向9。问:第一次记录时,时针指向几?四、回顾整理,反思提升师:通过这节课的学习你有什么收获? 板书设计: 植树问题 棵数=间隔数+1 间隔数=棵数-1 100÷5+1=21棵
作 业 设 计
基础:1.填一填。(1)下面的线段有( )个点,共有( )小段,不封闭图形的点数和段数的关系是( )。 (2)在一条长300米的公路两边种树,每隔4米种1棵(两端都要种),这样一共要种( )棵。 (3)如下图,在一条防风带上每隔30米种1棵树,这条防风带共种( )棵树,由此可以推断出两端都种树时,树的棵树比间隔数( )。综合:2.选一选:(1)一个圆形花坛的周长是36米,每隔4米摆一盆花,一共需要( )盆花。 A.8 B.9 C.10 D.11(2)一座楼房每上一层要16个台阶,小红每天回家要走80个台阶,小红家住( )楼。 A.5 B.6 C.7 D.8拓展提升:3.一条走廊长24米,每隔3米放一盆花,走廊两端都要放。一共要放多少盆花?
教学反思:
20m
5m
20m
5m
● ● ● ● ● ● ●
1500米
……
