2021学年暑假 九年级上册人教版数学衔接班讲义第8讲:二次函数y=a(x-h)2+k的图象与性质(无答案)
文档属性
| 名称 | 2021学年暑假 九年级上册人教版数学衔接班讲义第8讲:二次函数y=a(x-h)2+k的图象与性质(无答案) | 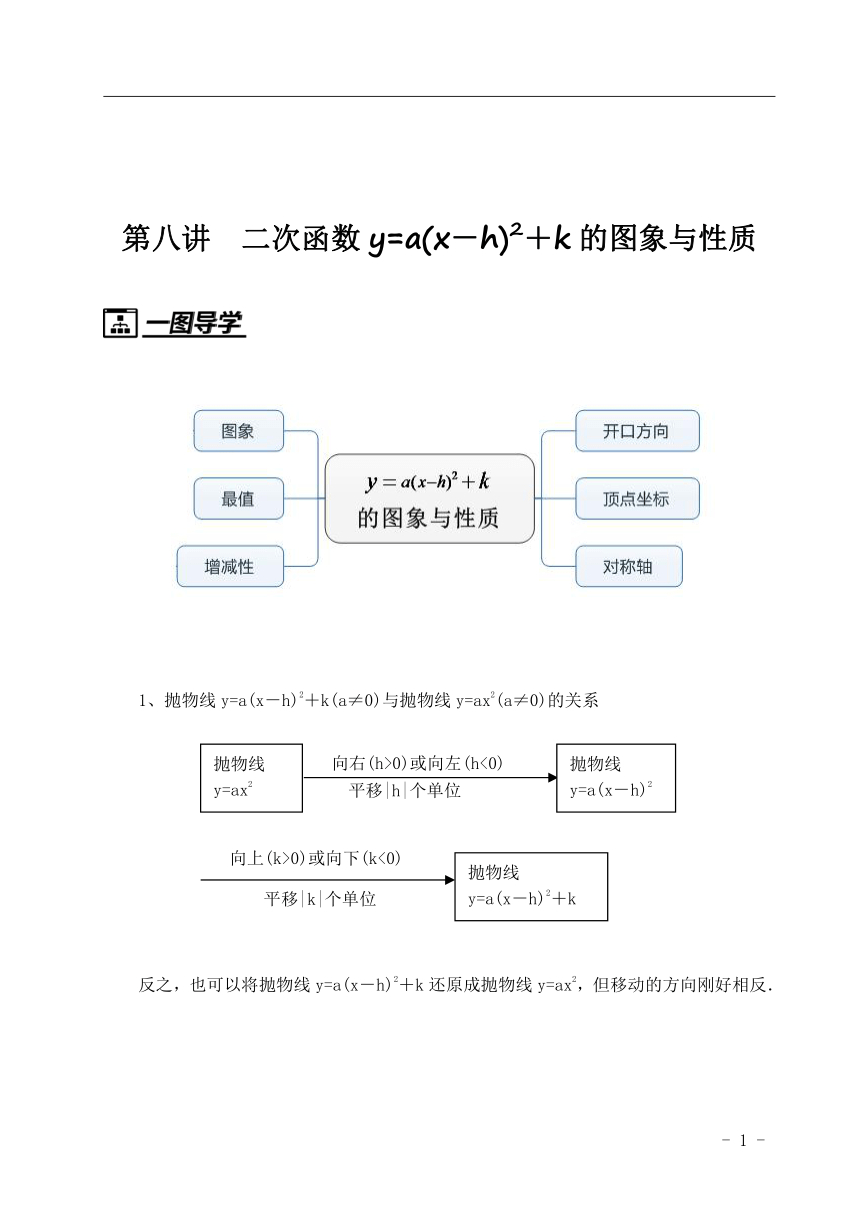 | |
| 格式 | docx | ||
| 文件大小 | 152.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 10:15:49 | ||
图片预览


文档简介
二次函数y=a(x-h)2+k的图象与性质
1、抛物线y=a(x-h)2+k(a≠0)与抛物线y=ax2(a≠0)的关系
反之,也可以将抛物线y=a(x-h)2+k还原成抛物线y=ax2,但移动的方向刚好相反.
2、抛物线y=a(x-h)2+k(a≠0)的性质
函数
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
图像
对称轴
x=h
x=h
顶点坐标
(h,k)
(h,k)
增减性
在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大
在对称轴的左侧,y随x的增大而增大;在对称轴的右侧,y随x的增大而减小
最值
当x=h时,y有最小值k
当x=h时,y有最大值k
例1、已知二次函数y=-2(x+1)2-3.
(1)抛物线y=-2(x+1)2-3的顶点坐标是________,对称轴方程是________,y有最______值为________;
(2)将二次函数y=-2x2的图象向_______平移________个单位,再向_______平移_______个单位,可得二次函数y=-2(x+1)2-3的图象.
例2、设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系为(
)
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y2>y1>y3
总结:比较两个二次函数值大小的方法
例3、已知二次函数y=(x+m)2+k的顶点为(1,-4).
(1)求二次函数的解析式及图象与x轴交于A、B两点的坐标.
(2)将二次函数的图象沿x轴翻折,得到一个新的抛物线,求新抛物线的解析式.
例4、二次函数y=ax2+bx+c的图象向左平移3个单位,再向下平移3个单位,得到二次函数y=(x-3)2+1,求a、b、c的值.
例5、如图,在平面直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数的图象向右平移几个单位长度,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
1、函数y=-2(x+1)2+3的顶点坐标为(???
)
?
A.(1,3)???
B.(-1,3)?
C.(1,-3)?
D.(-1,-3)
2、对于二次函数y=(x-1)2+2的图象,下列说法正确的是(???
)
A.开口向下
B.对称轴是x=-1
C.顶点坐标是(1,2)
D.与x轴有两个交点
3、将抛物线y=4x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数解析式为____________.
4、函数y=a(x-1)2+b与y=ax+b在同一坐标系中的图象大致为(???
)
5、指出下面函数图象的开口方向、对称轴、顶点坐标、最值.
(1)y=2(x+3)2+5;
(2)y=-3(x-1)2-2.
6、已知抛物线的顶点为(4,-8),并且经过点(6,-4),试确定此抛物线的解析式.?
1、抛物线y=a(x-h)2+k(a≠0)与抛物线y=ax2(a≠0)的关系
反之,也可以将抛物线y=a(x-h)2+k还原成抛物线y=ax2,但移动的方向刚好相反.
2、抛物线y=a(x-h)2+k(a≠0)的性质
函数
y=a(x-h)2+k(a>0)
y=a(x-h)2+k(a<0)
图像
对称轴
x=h
x=h
顶点坐标
(h,k)
(h,k)
增减性
在对称轴的左侧,y随x的增大而减小;在对称轴的右侧,y随x的增大而增大
在对称轴的左侧,y随x的增大而增大;在对称轴的右侧,y随x的增大而减小
最值
当x=h时,y有最小值k
当x=h时,y有最大值k
例1、已知二次函数y=-2(x+1)2-3.
(1)抛物线y=-2(x+1)2-3的顶点坐标是________,对称轴方程是________,y有最______值为________;
(2)将二次函数y=-2x2的图象向_______平移________个单位,再向_______平移_______个单位,可得二次函数y=-2(x+1)2-3的图象.
例2、设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+a上的三点,则y1,y2,y3的大小关系为(
)
A.y1>y2>y3
B.y1>y3>y2
C.y3>y2>y1
D.y2>y1>y3
总结:比较两个二次函数值大小的方法
例3、已知二次函数y=(x+m)2+k的顶点为(1,-4).
(1)求二次函数的解析式及图象与x轴交于A、B两点的坐标.
(2)将二次函数的图象沿x轴翻折,得到一个新的抛物线,求新抛物线的解析式.
例4、二次函数y=ax2+bx+c的图象向左平移3个单位,再向下平移3个单位,得到二次函数y=(x-3)2+1,求a、b、c的值.
例5、如图,在平面直角坐标系内,二次函数图象的顶点为A(1,-4),且过点B(3,0).
(1)求该二次函数的解析式;
(2)将该二次函数的图象向右平移几个单位长度,可使平移后所得图象经过坐标原点?并直接写出平移后所得图象与x轴的另一个交点的坐标.
1、函数y=-2(x+1)2+3的顶点坐标为(???
)
?
A.(1,3)???
B.(-1,3)?
C.(1,-3)?
D.(-1,-3)
2、对于二次函数y=(x-1)2+2的图象,下列说法正确的是(???
)
A.开口向下
B.对称轴是x=-1
C.顶点坐标是(1,2)
D.与x轴有两个交点
3、将抛物线y=4x2向左平移2个单位长度,再向下平移3个单位长度,得到的抛物线的函数解析式为____________.
4、函数y=a(x-1)2+b与y=ax+b在同一坐标系中的图象大致为(???
)
5、指出下面函数图象的开口方向、对称轴、顶点坐标、最值.
(1)y=2(x+3)2+5;
(2)y=-3(x-1)2-2.
6、已知抛物线的顶点为(4,-8),并且经过点(6,-4),试确定此抛物线的解析式.?
同课章节目录
