23.1 图形的旋转 课件 人教版数学 九年级 上册(共83张ppt)
文档属性
| 名称 | 23.1 图形的旋转 课件 人教版数学 九年级 上册(共83张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 25.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 10:43:13 | ||
图片预览









文档简介
图形的旋转
通过观察具体实例学习旋转概念,会画一个图形作旋转后所得的图形.
探究旋转的性质,并在观察、猜想、验证、归纳、概括的探究过程中,发展合情推理能力,进一步体会图形运动中的变和不变.
理解选择不同的旋转中心、不同的旋转角度对某一图案作旋转,会出现不同的效果,掌握根据需要用旋转的知识设计出美丽的图案.
教学目标
教学重点
教学难点
旋转的性质.
根据需要设计美丽图案.
运用旋转研究几何问题.
下列现象有什么特点?
指针式钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.这些现象有哪些共同特点?
把一个平面图形绕着平面内某一点 O 转动一个角度的图形变换叫做图形的旋转.这个点 O 叫旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过旋转变为点 P ′,
那么这两个点叫做这个旋转的对应点.
定义
1.请你举出一些现实生活、生产中旋转的实例,
? ? ? 并指出旋转中心和旋转角.
练习
练习
2.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转
? ? ? 的旋转角是多少度?从上午 9 时到上午 10 时呢?
练习
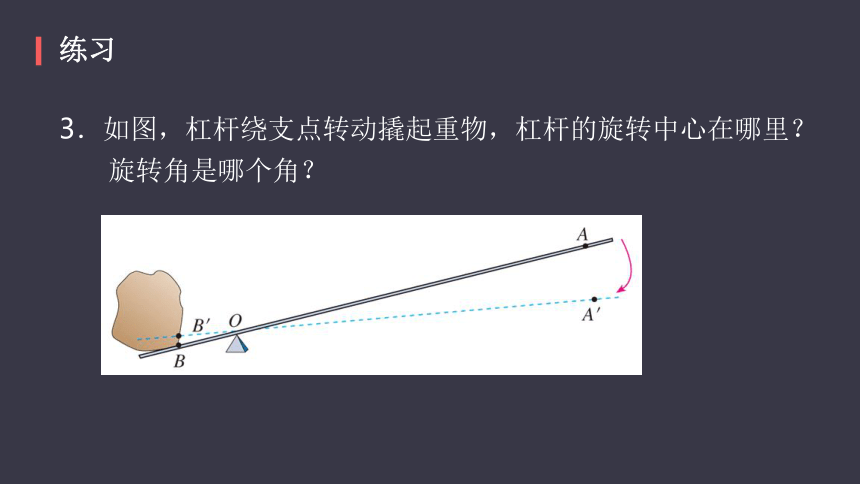
3.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?
? ? ? 旋转角是哪个角??
如图,ΔABC 是等腰三角形, ∠BAC = 36°,D 是 BC 上一点,ΔABD 经过旋转后到达?ΔACE 的位置,?
(1) 旋转中心是哪一点?
(2) 旋转了多少度??
(3) 如果 M 是 AB 的中点,那么经过上述旋转后,点 M 转到了
? ? ? 什么位置?
练习
答案:(1)A;(2)36°;(3)AC 的中点.
练习
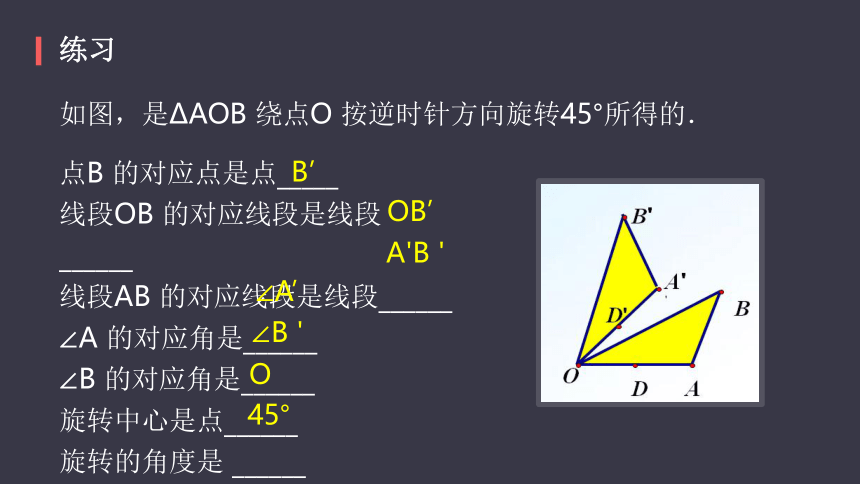
如图,是ΔAOB 绕点O 按逆时针方向旋转45°所得的.
点B 的对应点是点_____
线段OB 的对应线段是线段______
线段AB 的对应线段是线段______
∠A 的对应角是______
∠B 的对应角是______
旋转中心是点______
旋转的角度是 ______
B’
OB’
A'B '?
∠A’
∠B '?
O
45°
练习
图是由正方形ABCD 旋转而成.
(1)旋转中心是__________
(2)旋转的角度是_________
(3)若正方形的边长是1,则C ’D =_________
A
45°
练习
下列现象中属于旋转的有_______个
①地下水位逐年下降;②传送带的移动;
③方向盘的转动;④水龙头开关的转动;
⑤钟摆的运动;⑥荡秋千运动.
4
练习
如图正方形CDEF 旋转后能与正方形ABCD 重合,若O 是CD 的中点那么图形上可以作为旋转中心的点是______________.
D,C,O
探究
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O 作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(Δ?ABC ),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(Δ?A’B ’C ’ ),移开硬纸板.
探究
(1)线段 OA 和 OA’?有什么关系?
(2)∠AOA’ 和 ∠BOB ’有什么关系?
相等
(3)图中还有哪些类似关系的线段和角?
(4)Δ?ABC 和?Δ?A’B ’C ’ 有什么关系?
全等
OB =OB ’,OC =OC ’
∠COC ’=∠BOB ’=∠AOA’
归纳
旋转的性质
1.对应点到旋转中心的距离______.
2.对应点与旋转中心所连线段的夹角
? ? ? 等于_______.
3.旋转前、后的图形_______.
相等
旋转角
全等
练习
1、如图,小明坐在秋千上, 秋千旋转了80°.?请在图中小明身上
? ? ? 任意选一点P,利用旋转性质,标出点P 的对应点.
(1) 这两个点到旋转中心的距离有怎样的关系?
(2) 这两个点与旋转中心所连线段的夹角是多少度?
练习
2、如图,用左面的三角形经过怎样的旋转,可以得到右面的图形?
练习
3、找出图中扳手拧螺母时的旋转中心和旋转角
练习
ΔA'OB '是ΔAOB 绕点O按逆时针方向旋转得到的. 已知∠AOB =20°,∠A'OB =24°,AB =3,OA =5
则A'B '=____,OA' =____,旋转角 =______.
3
5
44°
练习
如图,ΔABC绕 A 逆时针旋转使得 C 点落在 BC 边上的 F 处,
则对于结论:
①AC =AF;
②∠FAB =∠EAB;
③EF =BC;
④∠EAB =∠FAC,
其中正确的结论是______________.
①③④
练习
如图E 是正方形ABCD 内一点,将ΔABE 绕点B 顺时针方向旋转到ΔCBF,其中EB =3cm,则BF =_____cm ,∠EBF =______.
答案:3,90°.
练习
如图将RtΔABC 绕C 点逆时针旋转30°后,点B 落在B ′,点A落在A’点位置,若A’C ⊥ AB,求∠B ’A’C 的度数.?
答案:60°.?
练习
如图将RtΔABC 绕C 点逆时针旋转30°后,点B 落在B ′,点A落在A’点位置,若A’C ⊥ AB,与∠B'A'C相等的角有几个.?
答案:3个.?
练习
如图∠C =30°,ΔABC 绕A点逆时针旋转 30° 后得到ΔAB 'C ',则图中度数是 30° 的角有________个.
答案:4个.?
例题
如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把ΔADE 顺时针旋转 90°,画出旋转后的图形.
怎么确定旋转后的图形呢?
关键是要确定三个顶点的对应点.
归纳
旋转图形的画法
1.根据旋转的性质确定关键点的对应点.
2.根据关键点确定旋转后的图形.
画出将线段 AB 绕点 O 按顺时针方向旋转 90° 后的图形.
练习
A
B
?
O
A'
B'
练习
画出将ΔABC 绕点C 按逆时针方向旋转150°后的对应三角形.?
练习
画出下图所示的四边形 ABCD 以 O 点为中心,旋转角为 30° 的旋转图形.
提示:要考虑到顺时针和逆时针两种可能.
练习
画出下图所示的四边形 ABCD 以 O 点为中心,旋转角为 60° 的旋转图形.
提示:要考虑到顺时针和逆时针两种可能.
练习
如图,ΔAOB 绕 O 点旋转后,G 点是 B 点的对应点,作出
?ΔAOB 旋转后的三角形.
提示:连接GO,∠BOG 就是旋转角.?
网格中旋转90°
下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将ΔOAB 绕点 O 逆时针旋转 90°, 你能画出ΔOAB 旋转后的图形ΔO 'A 'B ' 吗?
在网格中画旋转90°有什么技巧呢?
可以找到点与旋转中心所在的矩形,
通过旋转这个矩形确定对应点.
B '
网格中旋转90°的画法
归纳
1.确定关键点与旋转中心所在的矩形.
2.搞清楚是顺时针还是逆时针,旋转矩形,确定对应点.
3.确定旋转后的图形.
【分析】
【解答】
【点评】
网格中旋转90°
如何确定旋转中心
如图,ΔDEF 是由ΔABC 绕某一中心旋转一定的角度得到,请你找出这旋转中心.
归纳
确定旋转中心的步骤
1.连接两组对应点.
2.作对应点连线的垂直平分线.
3.交点就是旋转中心.
O
练习
在如图4×4的正方形网格中, ??ΔMNP绕某点旋转一定的角度,得到ΔM1N1P1,则其旋转中心是点_______.
B
练习
如图,将ΔABC 绕点P 顺时针旋转90°得到ΔA1B1C1,则点 P 的坐标是___________.
(1,2)
旋转效果
选择不同的旋转中心、不同的旋转角旋转同一个图形会出现不同的效果
旋转中心不变,改变旋转角
O
O
旋转效果
选择不同的旋转中心、不同的旋转角旋转同一个图形会出现不同的效果
旋转角不变,改变旋转中心
O1
O2
添加动态课件
设计图案
我们可以借助旋转设计出许多美丽的图案
例题
如下图是某一种花的花瓣和中心,现以 O 为旋转中心画出分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的这种花的图形.
O
练习
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
练习
香港特别行政区区旗中央的紫荆花图案是怎样形成的?
旋转出等腰
总结:旋转出等腰
如图,正方形A'B 'C 'D '是正方形ABCD按顺时针方向旋转45°而成的
(1)若AB=4,
则S正方形A'B'C'D'=__________;
(2)∠BAB '=? ? ? ? ? ? ? ? ? ?,
∠B 'AD=? ? ? ? ? ? ? ? ?;
(3)若连接BB ',
则∠B 'BA=? ? ? ? ? ? ? ? ?.
16
45°
45°
67.5°
旋转特殊角度
已知:如图,在ΔABC 中,∠BAC =120°,以 BC 为边向形外作等边三角形ΔBCD,把ΔABD 绕着点 D 按顺时针方向旋转60°后得到ΔECD,若AB =3,AC =2,求∠BAD 的度数与AD 的长.
答案:60°,5.
总结:旋转60°会产生等边三角形.
直角绕正方形中心旋转
已知,如图正方形 EFOG 绕与之边长相等的正方形 ABCD 的中心 O 旋转任意角度.求证图中阴影部分的面积等于正方形面积的四分之一.
提示:连接AO,BO,证明三角形全等.
与旋转有关的最值问题
如图,已知半圆的半径为 2,点 E 是圆上的动点,四边形 BCDE 是正方形,则 OD 的最大值为____________.
与旋转有关的最值问题1
如图,已知半圆的半径为 2,点 E 是圆上的动点,四边形 BCDE 是正方形,则 OD 的最大值为____________.
与旋转有关的最值问题2
如图, ????????????? ? ? ? ? ? ? ?,? ? ? ? ? ? ? ? ????????????? ,以 AB 为一边作正方形 ABCD,使 P,D 两点分别在直线 AB 两侧,当 P 与 D 距离最大时,正方形 ABCD 的面积为____________.
与旋转有关的最值问题2
30
如图, ????????????? ? ? ? ? ? ? ?,? ? ? ? ? ? ? ? ????????????? ,以 AB 为一边作正方形 ABCD,使 P,D 两点分别在直线 AB 两侧,当 P 与 D 距离最大时,正方形 ABCD 的面积为____________.
与旋转有关的规律问题
如图,在坐标系中放置一菱形ABCD,已知∠ABC =60°,OA=1.先将菱形ABCD 沿 x 轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1, B2, B3,…, 则B2015的坐标为_______________.
互补四边形半角模型
【分析】
【解答】
【点评】
互补四边形半角模型
【分析】
【解答】
【点评】
等腰直角三角形半角模型
【分析】
【解答】
如图,在Rt?ΔABC 中,∠BAC =90°,AC =AB,∠DAE =45°,且BD =3,CE =4,则ΔADE 的面积为__________.
总结
旋转的性质
1.对应点到旋转中心的距离______.
2.对应点与旋转中心所连线段的夹角等于_______.
3.旋转前、后的图形_______.
旋转图形的画法
1.根据旋转的性质确定关键点的对应点.
2.根据关键点确定旋转后的图形.
相等
旋转角
全等
总结
确定旋转中心的步骤
1.连接两组对应点.
2.作对应点连线的垂直平分线.
3.交点就是旋转中心.
O
总结
对比平移、轴对称,旋转的性质,
它们有哪些相同点和不同点?
相同点
不同点
平移
对应点连线平行
(共线)且相等
轴对称
变换前后,图形都全等
对应点连线被对称轴垂直平分
旋转
对应点到旋转中心距离相等
复习巩固
1. 任意画一个ΔABC,作下列旋转:
(1)以点A 为中心,把ΔABC 逆时针旋转40°;
(2)以点B 为中心,把ΔABC 逆时针旋转60°;
(3)在ΔABC 外任取一点为中心,把ΔABC 顺时针旋转120°;
(4)以AC 的中点为中心,把ΔABC 旋转180°.
复习巩固
2. 说出如图所示的压水机压水时的旋转中心和旋转角.
复习巩固
3.?ΔABC 中,AB =AC,P 是BC 边上任意一点,以点A 为中心,取旋转角等于∠BAC ,把ΔABP 逆时针旋转,画出旋转后的图形.
复习巩固
4. 分别画出ΔABC 绕点O 逆时针旋转 90° 和 180° 后的图形.
复习巩固
5. 下面的图形是由一个基本的图形经过旋转得到的,分别指出它们的旋转中心和旋转角.
综合运用
6. 把图中的五角星图案,绕着他的中心点O 旋转,旋转角至少为多少度时,旋转后的五角星能与自身重合,对等边三角形进行类似的讨论.
综合运用
7. 图中的风车图案,可以由哪个基本的图形,经过什么样的旋转得到?
综合运用
8. 如图,用一个等腰三角形,经过旋转,制作一个五角星图案.(提示,选择旋转中心,计算旋转角.)
综合运用
9. 如图,ΔABC 中,∠C =90°.
? ?(1)将ΔABC 绕点B 逆时针旋转90°,画出旋转后的三角形;
? ?(2)若BC =3,AC =4,点A旋转后的对应点为A',求A'A的长.
拓广探索
10. 如图,ΔABD,ΔAEC 都是等边三角形.BD 与 DC 有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
拓广探索
11. 以原点为中心,把点A(4,5)逆时针旋转90°,得到点B . 求点B的坐标.
通过观察具体实例学习旋转概念,会画一个图形作旋转后所得的图形.
探究旋转的性质,并在观察、猜想、验证、归纳、概括的探究过程中,发展合情推理能力,进一步体会图形运动中的变和不变.
理解选择不同的旋转中心、不同的旋转角度对某一图案作旋转,会出现不同的效果,掌握根据需要用旋转的知识设计出美丽的图案.
教学目标
教学重点
教学难点
旋转的性质.
根据需要设计美丽图案.
运用旋转研究几何问题.
下列现象有什么特点?
指针式钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.这些现象有哪些共同特点?
把一个平面图形绕着平面内某一点 O 转动一个角度的图形变换叫做图形的旋转.这个点 O 叫旋转中心,转动的角叫做旋转角.
如果图形上的点 P 经过旋转变为点 P ′,
那么这两个点叫做这个旋转的对应点.
定义
1.请你举出一些现实生活、生产中旋转的实例,
? ? ? 并指出旋转中心和旋转角.
练习
练习
2.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转
? ? ? 的旋转角是多少度?从上午 9 时到上午 10 时呢?
练习
3.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?
? ? ? 旋转角是哪个角??
如图,ΔABC 是等腰三角形, ∠BAC = 36°,D 是 BC 上一点,ΔABD 经过旋转后到达?ΔACE 的位置,?
(1) 旋转中心是哪一点?
(2) 旋转了多少度??
(3) 如果 M 是 AB 的中点,那么经过上述旋转后,点 M 转到了
? ? ? 什么位置?
练习
答案:(1)A;(2)36°;(3)AC 的中点.
练习
如图,是ΔAOB 绕点O 按逆时针方向旋转45°所得的.
点B 的对应点是点_____
线段OB 的对应线段是线段______
线段AB 的对应线段是线段______
∠A 的对应角是______
∠B 的对应角是______
旋转中心是点______
旋转的角度是 ______
B’
OB’
A'B '?
∠A’
∠B '?
O
45°
练习
图是由正方形ABCD 旋转而成.
(1)旋转中心是__________
(2)旋转的角度是_________
(3)若正方形的边长是1,则C ’D =_________
A
45°
练习
下列现象中属于旋转的有_______个
①地下水位逐年下降;②传送带的移动;
③方向盘的转动;④水龙头开关的转动;
⑤钟摆的运动;⑥荡秋千运动.
4
练习
如图正方形CDEF 旋转后能与正方形ABCD 重合,若O 是CD 的中点那么图形上可以作为旋转中心的点是______________.
D,C,O
探究
在硬纸板上,挖一个三角形洞,再另挖一个小洞 O 作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(Δ?ABC ),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(Δ?A’B ’C ’ ),移开硬纸板.
探究
(1)线段 OA 和 OA’?有什么关系?
(2)∠AOA’ 和 ∠BOB ’有什么关系?
相等
(3)图中还有哪些类似关系的线段和角?
(4)Δ?ABC 和?Δ?A’B ’C ’ 有什么关系?
全等
OB =OB ’,OC =OC ’
∠COC ’=∠BOB ’=∠AOA’
归纳
旋转的性质
1.对应点到旋转中心的距离______.
2.对应点与旋转中心所连线段的夹角
? ? ? 等于_______.
3.旋转前、后的图形_______.
相等
旋转角
全等
练习
1、如图,小明坐在秋千上, 秋千旋转了80°.?请在图中小明身上
? ? ? 任意选一点P,利用旋转性质,标出点P 的对应点.
(1) 这两个点到旋转中心的距离有怎样的关系?
(2) 这两个点与旋转中心所连线段的夹角是多少度?
练习
2、如图,用左面的三角形经过怎样的旋转,可以得到右面的图形?
练习
3、找出图中扳手拧螺母时的旋转中心和旋转角
练习
ΔA'OB '是ΔAOB 绕点O按逆时针方向旋转得到的. 已知∠AOB =20°,∠A'OB =24°,AB =3,OA =5
则A'B '=____,OA' =____,旋转角 =______.
3
5
44°
练习
如图,ΔABC绕 A 逆时针旋转使得 C 点落在 BC 边上的 F 处,
则对于结论:
①AC =AF;
②∠FAB =∠EAB;
③EF =BC;
④∠EAB =∠FAC,
其中正确的结论是______________.
①③④
练习
如图E 是正方形ABCD 内一点,将ΔABE 绕点B 顺时针方向旋转到ΔCBF,其中EB =3cm,则BF =_____cm ,∠EBF =______.
答案:3,90°.
练习
如图将RtΔABC 绕C 点逆时针旋转30°后,点B 落在B ′,点A落在A’点位置,若A’C ⊥ AB,求∠B ’A’C 的度数.?
答案:60°.?
练习
如图将RtΔABC 绕C 点逆时针旋转30°后,点B 落在B ′,点A落在A’点位置,若A’C ⊥ AB,与∠B'A'C相等的角有几个.?
答案:3个.?
练习
如图∠C =30°,ΔABC 绕A点逆时针旋转 30° 后得到ΔAB 'C ',则图中度数是 30° 的角有________个.
答案:4个.?
例题
如图, E 是正方形 ABCD 中 CD 边上任意一点,以点 A 为中心,把ΔADE 顺时针旋转 90°,画出旋转后的图形.
怎么确定旋转后的图形呢?
关键是要确定三个顶点的对应点.
归纳
旋转图形的画法
1.根据旋转的性质确定关键点的对应点.
2.根据关键点确定旋转后的图形.
画出将线段 AB 绕点 O 按顺时针方向旋转 90° 后的图形.
练习
A
B
?
O
A'
B'
练习
画出将ΔABC 绕点C 按逆时针方向旋转150°后的对应三角形.?
练习
画出下图所示的四边形 ABCD 以 O 点为中心,旋转角为 30° 的旋转图形.
提示:要考虑到顺时针和逆时针两种可能.
练习
画出下图所示的四边形 ABCD 以 O 点为中心,旋转角为 60° 的旋转图形.
提示:要考虑到顺时针和逆时针两种可能.
练习
如图,ΔAOB 绕 O 点旋转后,G 点是 B 点的对应点,作出
?ΔAOB 旋转后的三角形.
提示:连接GO,∠BOG 就是旋转角.?
网格中旋转90°
下图为 4×4 的正方形网格,每个小正方形的边长均为 1,将ΔOAB 绕点 O 逆时针旋转 90°, 你能画出ΔOAB 旋转后的图形ΔO 'A 'B ' 吗?
在网格中画旋转90°有什么技巧呢?
可以找到点与旋转中心所在的矩形,
通过旋转这个矩形确定对应点.
B '
网格中旋转90°的画法
归纳
1.确定关键点与旋转中心所在的矩形.
2.搞清楚是顺时针还是逆时针,旋转矩形,确定对应点.
3.确定旋转后的图形.
【分析】
【解答】
【点评】
网格中旋转90°
如何确定旋转中心
如图,ΔDEF 是由ΔABC 绕某一中心旋转一定的角度得到,请你找出这旋转中心.
归纳
确定旋转中心的步骤
1.连接两组对应点.
2.作对应点连线的垂直平分线.
3.交点就是旋转中心.
O
练习
在如图4×4的正方形网格中, ??ΔMNP绕某点旋转一定的角度,得到ΔM1N1P1,则其旋转中心是点_______.
B
练习
如图,将ΔABC 绕点P 顺时针旋转90°得到ΔA1B1C1,则点 P 的坐标是___________.
(1,2)
旋转效果
选择不同的旋转中心、不同的旋转角旋转同一个图形会出现不同的效果
旋转中心不变,改变旋转角
O
O
旋转效果
选择不同的旋转中心、不同的旋转角旋转同一个图形会出现不同的效果
旋转角不变,改变旋转中心
O1
O2
添加动态课件
设计图案
我们可以借助旋转设计出许多美丽的图案
例题
如下图是某一种花的花瓣和中心,现以 O 为旋转中心画出分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的这种花的图形.
O
练习
把一个三角形进行旋转:
(1)选择不同的旋转中心、不同的旋转角,看看旋转的效果;
(2)改变三角形的形状,看看旋转的效果.
练习
香港特别行政区区旗中央的紫荆花图案是怎样形成的?
旋转出等腰
总结:旋转出等腰
如图,正方形A'B 'C 'D '是正方形ABCD按顺时针方向旋转45°而成的
(1)若AB=4,
则S正方形A'B'C'D'=__________;
(2)∠BAB '=? ? ? ? ? ? ? ? ? ?,
∠B 'AD=? ? ? ? ? ? ? ? ?;
(3)若连接BB ',
则∠B 'BA=? ? ? ? ? ? ? ? ?.
16
45°
45°
67.5°
旋转特殊角度
已知:如图,在ΔABC 中,∠BAC =120°,以 BC 为边向形外作等边三角形ΔBCD,把ΔABD 绕着点 D 按顺时针方向旋转60°后得到ΔECD,若AB =3,AC =2,求∠BAD 的度数与AD 的长.
答案:60°,5.
总结:旋转60°会产生等边三角形.
直角绕正方形中心旋转
已知,如图正方形 EFOG 绕与之边长相等的正方形 ABCD 的中心 O 旋转任意角度.求证图中阴影部分的面积等于正方形面积的四分之一.
提示:连接AO,BO,证明三角形全等.
与旋转有关的最值问题
如图,已知半圆的半径为 2,点 E 是圆上的动点,四边形 BCDE 是正方形,则 OD 的最大值为____________.
与旋转有关的最值问题1
如图,已知半圆的半径为 2,点 E 是圆上的动点,四边形 BCDE 是正方形,则 OD 的最大值为____________.
与旋转有关的最值问题2
如图, ????????????? ? ? ? ? ? ? ?,? ? ? ? ? ? ? ? ????????????? ,以 AB 为一边作正方形 ABCD,使 P,D 两点分别在直线 AB 两侧,当 P 与 D 距离最大时,正方形 ABCD 的面积为____________.
与旋转有关的最值问题2
30
如图, ????????????? ? ? ? ? ? ? ?,? ? ? ? ? ? ? ? ????????????? ,以 AB 为一边作正方形 ABCD,使 P,D 两点分别在直线 AB 两侧,当 P 与 D 距离最大时,正方形 ABCD 的面积为____________.
与旋转有关的规律问题
如图,在坐标系中放置一菱形ABCD,已知∠ABC =60°,OA=1.先将菱形ABCD 沿 x 轴的正方向无滑动翻转,每次翻转60°,连续翻转2015次,点B的落点依次为B1, B2, B3,…, 则B2015的坐标为_______________.
互补四边形半角模型
【分析】
【解答】
【点评】
互补四边形半角模型
【分析】
【解答】
【点评】
等腰直角三角形半角模型
【分析】
【解答】
如图,在Rt?ΔABC 中,∠BAC =90°,AC =AB,∠DAE =45°,且BD =3,CE =4,则ΔADE 的面积为__________.
总结
旋转的性质
1.对应点到旋转中心的距离______.
2.对应点与旋转中心所连线段的夹角等于_______.
3.旋转前、后的图形_______.
旋转图形的画法
1.根据旋转的性质确定关键点的对应点.
2.根据关键点确定旋转后的图形.
相等
旋转角
全等
总结
确定旋转中心的步骤
1.连接两组对应点.
2.作对应点连线的垂直平分线.
3.交点就是旋转中心.
O
总结
对比平移、轴对称,旋转的性质,
它们有哪些相同点和不同点?
相同点
不同点
平移
对应点连线平行
(共线)且相等
轴对称
变换前后,图形都全等
对应点连线被对称轴垂直平分
旋转
对应点到旋转中心距离相等
复习巩固
1. 任意画一个ΔABC,作下列旋转:
(1)以点A 为中心,把ΔABC 逆时针旋转40°;
(2)以点B 为中心,把ΔABC 逆时针旋转60°;
(3)在ΔABC 外任取一点为中心,把ΔABC 顺时针旋转120°;
(4)以AC 的中点为中心,把ΔABC 旋转180°.
复习巩固
2. 说出如图所示的压水机压水时的旋转中心和旋转角.
复习巩固
3.?ΔABC 中,AB =AC,P 是BC 边上任意一点,以点A 为中心,取旋转角等于∠BAC ,把ΔABP 逆时针旋转,画出旋转后的图形.
复习巩固
4. 分别画出ΔABC 绕点O 逆时针旋转 90° 和 180° 后的图形.
复习巩固
5. 下面的图形是由一个基本的图形经过旋转得到的,分别指出它们的旋转中心和旋转角.
综合运用
6. 把图中的五角星图案,绕着他的中心点O 旋转,旋转角至少为多少度时,旋转后的五角星能与自身重合,对等边三角形进行类似的讨论.
综合运用
7. 图中的风车图案,可以由哪个基本的图形,经过什么样的旋转得到?
综合运用
8. 如图,用一个等腰三角形,经过旋转,制作一个五角星图案.(提示,选择旋转中心,计算旋转角.)
综合运用
9. 如图,ΔABC 中,∠C =90°.
? ?(1)将ΔABC 绕点B 逆时针旋转90°,画出旋转后的三角形;
? ?(2)若BC =3,AC =4,点A旋转后的对应点为A',求A'A的长.
拓广探索
10. 如图,ΔABD,ΔAEC 都是等边三角形.BD 与 DC 有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
拓广探索
11. 以原点为中心,把点A(4,5)逆时针旋转90°,得到点B . 求点B的坐标.
同课章节目录
