1.5.1乘方课件2020-2021学年人教版 七年级数学上册(共67张ppt)
文档属性
| 名称 | 1.5.1乘方课件2020-2021学年人教版 七年级数学上册(共67张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 10:44:45 | ||
图片预览










文档简介
乘方
教学目标
利用有理数的乘方进行运算.
掌握有理数的混合运算.
教学重点
教学难点
有理数乘方的表示方法及运算.
有理数乘方的运算.??
有理数的混合运算.
一张厚为0.1毫米的纸对折27次后,它的厚度相当于1.5个珠穆朗玛峰.
你信吗?
这是真的!?
假如你穿越到300年前,给自己存100块钱,按照每年4%的年化收益率计算,到今天你大概能拿到多少钱?
算一下前几年的.?
第一年:100×1.04=104
第二年:100×1.04 ?≈ 108
第三年:100×1.04 ?≈ 112
第四年:100×1.04 ?≈ 117?
大胆预测一下,大概有多少钱.?
A.几万
B.几十万
C.上百万
D.上千万
都能在北京四环买套房了!?
2
4
3
1、边长为a的正方形的面积为____;
2、棱长为a的正方体的体积为____;?
3、(-2)×(-2)×(-2)=____;?
4、(-1)×(-2)×(-3)×(-4)×5=____;?
5、(-1)×(-1)×(-1)×(-1)×(-1)=____.
-8
120
-1
练一练
如图,一正方体的棱长为4cm, 则它的体积为_______立方厘米.
4×4×4
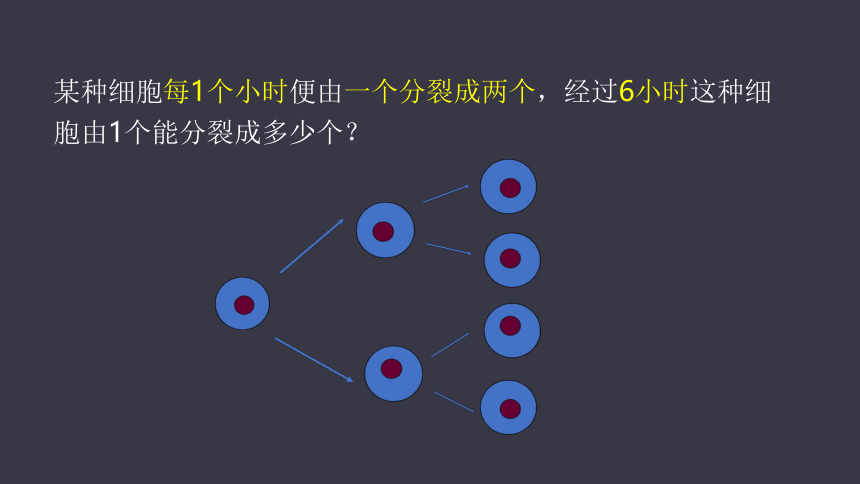
某种细胞每1个小时便由一个分裂成两个,经过6小时这种细胞由1个能分裂成多少个?
这个细胞分裂一次可得多少个细胞?
分裂两次呢?
分裂三次呢?
那么,分裂六次可得多少个细胞??
答:
2个
2×2个;
2×2×2个;
六次:
两次:
三次:
2×2×2×2×2×2个.
一次:
观察与归纳
正方体的体积式子: 4×4×4
它们有什么相同点?
它们都是乘法; 并且,它们各自的因数都相同.
细胞分裂六次后的个数式子: 2×2×2×2×2×2.
请比较:
乘方的定义
这样的运算,?
乘方:?求相同因数积的运算.
我们叫作乘方运算.
4×4×4记作:
2×2×2×2×2×2记作:?
一般的,任意多个相同的有理数相乘,我们通常记作:
(因数)
(因数的个数)
n个a相乘
a×a…×a
=?
口答练习
1)在? ? ? ? ?中,12是 _____ 数,10是 _____ 数,读作? ____________;??
2)? ? ? ? ? ?的底数是 _____,指数是? _____,读作? ____________;
12的10次方
底
指
的7次方
7
口答练习
3)在? ? ? ? ? ? 中,-3是 _____ 数,16是 _____ 数,读作? ____________;??
底
指
-3的16次方
4)在 ? ? ? ? ? ? 中,-a是 _____ 数,17是 _____ 数,读作? ____________;??
-a的17次方
底
指
口答练习
5)5看成幂的话,底数是______,指数是_____,可读作___________;
6) a看成幂的话,底数是_____ ,指数是_____,可读作___________;
5
a
1
1
5的一次方
a的一次方
练习
一、把下列乘法式子写成乘方的形式:
1. 1×1×1×1×1×1×1=_______?;?
2. 3×3×3×3×3=_______ ;??
3. (-3)×(-3)×(-3)×(-3)=______;??
4.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? =? ? ? ? ? ? ?;
练习
填空
底数?
指数?
幂?
-1?
2?
3?
5?
4?
书写时,底数如果是分数与负数时,它是一个整体要添上括号.
底数?
指数?
幂?
练习
二、把下列乘方写成乘法的形式:??
1.? ? ? ? ? ? ?=______________________________;?
2.? ? ? ? ? ? ?=______________________________;?
3.? ? ? ? ? ? ?=______________________________;
思考
用乘方式子怎么表示? ? 的相反数?
不同
表示? ? 的相反数
表示3个(-3)相乘
? ? ? 与 ? ? ? ? ? 的含义相同吗?
练习
判断下列各题是否正确:
(? ? ?)③? ?
(? ? ?)②??
(? ? ?)①? ?
(? ? ?)④? ?
练习
判断下列各题是否正确:
(? ? ?)②
(? ? ?)③
(? ? ?)④
(? ? ?)①
(? ? ?)⑤
例题
计算:
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.?
(1)
(2)
(3)
例题
例1 计算:
(1)? ? ? ? ? ? ? ? ? ? ? ? ? (2)? ? ? ? ? ? ? ? ? ? ? ? ? (3)
解:
你发现负数的幂的正负有什么规律吗?
负数的奇次幂是负数;偶次幂是正数.
奇负
(2)?
(3)
(1)?
=?
偶正
例题
(1)
(2)
计算:
想一想
观察刚才计算的结果,你能发现什么规律?
10的几次方,1后面就有几个0.?
=100
=1000
=10000
=10000
=-1000
=100
想一想
观察刚才计算的结果,你还能发现什么规律?
正数的任何次幂还是正数;
负数的奇次幂是负数;偶次幂是正数.
奇负
=100
=1000
=10000
=10000
=-1000
=100
偶正
幂的符号规律
负数的奇次幂是负数,偶次幂是正数.
正数的任何次幂还是正数;
0的任何正整数次幂都是0.
简称为奇负偶正.
你能迅速判断下列各幂的正负吗?
不计算下列各式的值,你能确定其符号吗?你能得到什么规律吗?说出你的根据.
(1)
(2)
(3)
(4)
(5)
(6)
例题
你能用计算器计算? ? ? ? ?和? ? ? ? 吗?
解:用带符号键(-)的计算器.
显示:(-8)^5
显示:(-3)^6
(? ? (-)? ?8? ?)? ^? 5? =
-32768
(? ? (-)? ?3? ?)? ^? 6? =
729
所以:
=
=
-32768
729
练习
(1)? ? ? ? ?中,底数、指数各是什么?? ??
(2)? ? ? ? ? ?中-10叫做什么数?8叫做什么数?
是正数还是负数?
1.
练习
2. 计算:
(1)
(5)
(2)
(3)
(4)
(6)
(7)
(8)
练习
3. 用计算器计算:
(1)
(2)
(4)
(3)
探究
设n为正整数
=
=
=
=
-1
-1
-1
-1
1
1
1
1
-1的奇数次方等于____.
-1的偶数次方等于____.
奇负
-1
1
归纳
偶正
=
=
=
=
练习
(3)? ??
(2)? ??
(1)
纸的层数与对称次数的关系
请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
如果对折n次,那么纸的层数是_____.
对折
次数
纸的
层数
层数可
表示为
1次
3次
4次
5次
2次
...
2
4
8
16
32
2
2×2
2×2×2
2×2×2×2
2×2×2×2×2
2
...
...
纸和珠穆朗玛
纸的厚度:
纸的厚度是珠穆朗玛峰高度的多少倍?
穿越存钱
地主与长工
? ?有一个长工到一个财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的平方.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少钱?
? ? 月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.
地主与长工
长工算法:
第一天1分,第二天2分,第三天4分,第四天16分,第五天256分……
财主算法:
第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……
棋盘上的学问
? ? ? 古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.
? ? ?大臣说:“就在这个棋盘上放一些米粒吧.第1格放1粒,第2格放2粒,第3格放4粒,然后是8粒、16粒、32粒、……一直到第64格.”
“你真傻! 就要这么一些米粒?!”国王哈哈大笑.大臣说:“就怕你的国库里没有这么多米!”
? ? ?你认为国王的国库里有这么多米吗?
拉面中的数学
请哪一位同学说说兰州拉面的制作过程.??
总结
这节课我们学到了什么?
1、乘方的概念:
2、幂的概念:
3、幂的符号规律:
求n个相同因数a乘积的运算.
负数的奇次幂是负数;偶次幂是正数.
正数的任何次幂还是正数;
0的任何正整数次幂都是0.
底数?
指数?
幂?
总结
这节课我们还学到了什么?
-1的奇数次方等于_____.
-1的偶数次方等于_____.
-1
1
1、什么是乘方?? ?
2、什么是幂,什么是底数,什么是指数???
3、怎么计算有理数的乘方?
利用乘法分配律巧算
知识回顾
1、乘方的概念:
2、幂的概念
求n个相同因数a乘积的运算.
n个a相乘
=a×a×a...×a
底数?
指数?
幂?
各种运算及其结果
运算
结果
加法
和
减法
差
乘法
积
除法
商
乘方
幂
加法、减法、乘法、除法、乘方
一个运算中,含有有理数的加、减、乘、除、乘方等多种运算,称为有理数的混合运算.
我们学习了哪些运算?
观察
问: 算式含有哪几种运算?
有理数混合运算的顺序是怎样的呢?
第三级运算
乘方运算
加减运算
第一级运算
乘除运算
第二级运算
有理数混合运算的顺序
1. 先_______、再______、最后______.
2. 同级运算,从_______到_______进行.
3. 如有括号,先做_______的运算,按小括号、中括号、大括号依次进行.
乘方
乘除
加减
左
右
括号内
例题
(2)
=2×(-27)-(-12)+15
=-54+12+15
=-27
=-8-54+4.5
=-57.5
(1)
一题多解
解法一: 原式
解法二: 原式
=?
=
=-6+(-5)
=-11??
-11
辨析运算顺序
有什么不同?
有什么不同?
有什么不同?
与
与
与
辨析运算顺序
=?
=
=
解: 原式 =
=?
解: 原式
=?
例题
例4 观察下列三行数:
-2, 4,-8, 16, -32,64,...;
0, 6,-6, 18, -30,66,...;
-1, 2,-4, 8, -16,32,...;
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
①
②
③
-2, 4,-8, 16, -32,64,...;
0, 6,-6, 18, -30,66,...;
-1, 2,-4, 8, -16,32,...;
例题
(3)取每行数的第10个数,计算这三个数的和.
②
③
①
练习
计算:
(1)
(2)
练习
计算:
(3)
(4)
练习
计算:
(1)
(2)
(3)
练习
计算:
(4)
(5)? ?
2的幂的末位数字规律
观察下列算式:
...根据上述算式中的规律,你认为 ? ? ? 的末位数字是( ).
答案:C
? A. 2?
B. 4?
C. 6?
D. 8
,
,
,
,
,
,
,
观察下列算式:
?探究计算结果中的个位数字的规律,猜测? ? ? ? +1的个位数字是______.
答案:8
3的幂的末位数字规律
,
,
,
,
.
幂比大小
答案:C
? ? ? ? ?比 ? ? ? ? ? ? 小 (? ? ?).?
A. 2
B. -2
C.?
D .
总结
这节课我们学到了什么?
有理数混合运算的顺序
1. 先_______、再______、最后______.
2. 同级运算,从______到_____进行.
3. 如有括号,先做_________的运算,按小括号、中括号、大括号依次行.
乘方
乘除?
加减?
左?
右
括号内?
1、有理数的混合运算包含哪些运算?
2、有理数混合运算的顺序是什么?
3、有理数混合运算需要注意些什么?
有理数的混合运算
教学目标
利用有理数的乘方进行运算.
掌握有理数的混合运算.
教学重点
教学难点
有理数乘方的表示方法及运算.
有理数乘方的运算.??
有理数的混合运算.
一张厚为0.1毫米的纸对折27次后,它的厚度相当于1.5个珠穆朗玛峰.
你信吗?
这是真的!?
假如你穿越到300年前,给自己存100块钱,按照每年4%的年化收益率计算,到今天你大概能拿到多少钱?
算一下前几年的.?
第一年:100×1.04=104
第二年:100×1.04 ?≈ 108
第三年:100×1.04 ?≈ 112
第四年:100×1.04 ?≈ 117?
大胆预测一下,大概有多少钱.?
A.几万
B.几十万
C.上百万
D.上千万
都能在北京四环买套房了!?
2
4
3
1、边长为a的正方形的面积为____;
2、棱长为a的正方体的体积为____;?
3、(-2)×(-2)×(-2)=____;?
4、(-1)×(-2)×(-3)×(-4)×5=____;?
5、(-1)×(-1)×(-1)×(-1)×(-1)=____.
-8
120
-1
练一练
如图,一正方体的棱长为4cm, 则它的体积为_______立方厘米.
4×4×4
某种细胞每1个小时便由一个分裂成两个,经过6小时这种细胞由1个能分裂成多少个?
这个细胞分裂一次可得多少个细胞?
分裂两次呢?
分裂三次呢?
那么,分裂六次可得多少个细胞??
答:
2个
2×2个;
2×2×2个;
六次:
两次:
三次:
2×2×2×2×2×2个.
一次:
观察与归纳
正方体的体积式子: 4×4×4
它们有什么相同点?
它们都是乘法; 并且,它们各自的因数都相同.
细胞分裂六次后的个数式子: 2×2×2×2×2×2.
请比较:
乘方的定义
这样的运算,?
乘方:?求相同因数积的运算.
我们叫作乘方运算.
4×4×4记作:
2×2×2×2×2×2记作:?
一般的,任意多个相同的有理数相乘,我们通常记作:
(因数)
(因数的个数)
n个a相乘
a×a…×a
=?
口答练习
1)在? ? ? ? ?中,12是 _____ 数,10是 _____ 数,读作? ____________;??
2)? ? ? ? ? ?的底数是 _____,指数是? _____,读作? ____________;
12的10次方
底
指
的7次方
7
口答练习
3)在? ? ? ? ? ? 中,-3是 _____ 数,16是 _____ 数,读作? ____________;??
底
指
-3的16次方
4)在 ? ? ? ? ? ? 中,-a是 _____ 数,17是 _____ 数,读作? ____________;??
-a的17次方
底
指
口答练习
5)5看成幂的话,底数是______,指数是_____,可读作___________;
6) a看成幂的话,底数是_____ ,指数是_____,可读作___________;
5
a
1
1
5的一次方
a的一次方
练习
一、把下列乘法式子写成乘方的形式:
1. 1×1×1×1×1×1×1=_______?;?
2. 3×3×3×3×3=_______ ;??
3. (-3)×(-3)×(-3)×(-3)=______;??
4.? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? =? ? ? ? ? ? ?;
练习
填空
底数?
指数?
幂?
-1?
2?
3?
5?
4?
书写时,底数如果是分数与负数时,它是一个整体要添上括号.
底数?
指数?
幂?
练习
二、把下列乘方写成乘法的形式:??
1.? ? ? ? ? ? ?=______________________________;?
2.? ? ? ? ? ? ?=______________________________;?
3.? ? ? ? ? ? ?=______________________________;
思考
用乘方式子怎么表示? ? 的相反数?
不同
表示? ? 的相反数
表示3个(-3)相乘
? ? ? 与 ? ? ? ? ? 的含义相同吗?
练习
判断下列各题是否正确:
(? ? ?)③? ?
(? ? ?)②??
(? ? ?)①? ?
(? ? ?)④? ?
练习
判断下列各题是否正确:
(? ? ?)②
(? ? ?)③
(? ? ?)④
(? ? ?)①
(? ? ?)⑤
例题
计算:
注意:当底数是负数或分数时,底数一定要加上括号,这也是辩认底数的方法.?
(1)
(2)
(3)
例题
例1 计算:
(1)? ? ? ? ? ? ? ? ? ? ? ? ? (2)? ? ? ? ? ? ? ? ? ? ? ? ? (3)
解:
你发现负数的幂的正负有什么规律吗?
负数的奇次幂是负数;偶次幂是正数.
奇负
(2)?
(3)
(1)?
=?
偶正
例题
(1)
(2)
计算:
想一想
观察刚才计算的结果,你能发现什么规律?
10的几次方,1后面就有几个0.?
=100
=1000
=10000
=10000
=-1000
=100
想一想
观察刚才计算的结果,你还能发现什么规律?
正数的任何次幂还是正数;
负数的奇次幂是负数;偶次幂是正数.
奇负
=100
=1000
=10000
=10000
=-1000
=100
偶正
幂的符号规律
负数的奇次幂是负数,偶次幂是正数.
正数的任何次幂还是正数;
0的任何正整数次幂都是0.
简称为奇负偶正.
你能迅速判断下列各幂的正负吗?
不计算下列各式的值,你能确定其符号吗?你能得到什么规律吗?说出你的根据.
(1)
(2)
(3)
(4)
(5)
(6)
例题
你能用计算器计算? ? ? ? ?和? ? ? ? 吗?
解:用带符号键(-)的计算器.
显示:(-8)^5
显示:(-3)^6
(? ? (-)? ?8? ?)? ^? 5? =
-32768
(? ? (-)? ?3? ?)? ^? 6? =
729
所以:
=
=
-32768
729
练习
(1)? ? ? ? ?中,底数、指数各是什么?? ??
(2)? ? ? ? ? ?中-10叫做什么数?8叫做什么数?
是正数还是负数?
1.
练习
2. 计算:
(1)
(5)
(2)
(3)
(4)
(6)
(7)
(8)
练习
3. 用计算器计算:
(1)
(2)
(4)
(3)
探究
设n为正整数
=
=
=
=
-1
-1
-1
-1
1
1
1
1
-1的奇数次方等于____.
-1的偶数次方等于____.
奇负
-1
1
归纳
偶正
=
=
=
=
练习
(3)? ??
(2)? ??
(1)
纸的层数与对称次数的关系
请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
如果对折n次,那么纸的层数是_____.
对折
次数
纸的
层数
层数可
表示为
1次
3次
4次
5次
2次
...
2
4
8
16
32
2
2×2
2×2×2
2×2×2×2
2×2×2×2×2
2
...
...
纸和珠穆朗玛
纸的厚度:
纸的厚度是珠穆朗玛峰高度的多少倍?
穿越存钱
地主与长工
? ?有一个长工到一个财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的平方.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少钱?
? ? 月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.
地主与长工
长工算法:
第一天1分,第二天2分,第三天4分,第四天16分,第五天256分……
财主算法:
第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……
棋盘上的学问
? ? ? 古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求.
? ? ?大臣说:“就在这个棋盘上放一些米粒吧.第1格放1粒,第2格放2粒,第3格放4粒,然后是8粒、16粒、32粒、……一直到第64格.”
“你真傻! 就要这么一些米粒?!”国王哈哈大笑.大臣说:“就怕你的国库里没有这么多米!”
? ? ?你认为国王的国库里有这么多米吗?
拉面中的数学
请哪一位同学说说兰州拉面的制作过程.??
总结
这节课我们学到了什么?
1、乘方的概念:
2、幂的概念:
3、幂的符号规律:
求n个相同因数a乘积的运算.
负数的奇次幂是负数;偶次幂是正数.
正数的任何次幂还是正数;
0的任何正整数次幂都是0.
底数?
指数?
幂?
总结
这节课我们还学到了什么?
-1的奇数次方等于_____.
-1的偶数次方等于_____.
-1
1
1、什么是乘方?? ?
2、什么是幂,什么是底数,什么是指数???
3、怎么计算有理数的乘方?
利用乘法分配律巧算
知识回顾
1、乘方的概念:
2、幂的概念
求n个相同因数a乘积的运算.
n个a相乘
=a×a×a...×a
底数?
指数?
幂?
各种运算及其结果
运算
结果
加法
和
减法
差
乘法
积
除法
商
乘方
幂
加法、减法、乘法、除法、乘方
一个运算中,含有有理数的加、减、乘、除、乘方等多种运算,称为有理数的混合运算.
我们学习了哪些运算?
观察
问: 算式含有哪几种运算?
有理数混合运算的顺序是怎样的呢?
第三级运算
乘方运算
加减运算
第一级运算
乘除运算
第二级运算
有理数混合运算的顺序
1. 先_______、再______、最后______.
2. 同级运算,从_______到_______进行.
3. 如有括号,先做_______的运算,按小括号、中括号、大括号依次进行.
乘方
乘除
加减
左
右
括号内
例题
(2)
=2×(-27)-(-12)+15
=-54+12+15
=-27
=-8-54+4.5
=-57.5
(1)
一题多解
解法一: 原式
解法二: 原式
=?
=
=-6+(-5)
=-11??
-11
辨析运算顺序
有什么不同?
有什么不同?
有什么不同?
与
与
与
辨析运算顺序
=?
=
=
解: 原式 =
=?
解: 原式
=?
例题
例4 观察下列三行数:
-2, 4,-8, 16, -32,64,...;
0, 6,-6, 18, -30,66,...;
-1, 2,-4, 8, -16,32,...;
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
①
②
③
-2, 4,-8, 16, -32,64,...;
0, 6,-6, 18, -30,66,...;
-1, 2,-4, 8, -16,32,...;
例题
(3)取每行数的第10个数,计算这三个数的和.
②
③
①
练习
计算:
(1)
(2)
练习
计算:
(3)
(4)
练习
计算:
(1)
(2)
(3)
练习
计算:
(4)
(5)? ?
2的幂的末位数字规律
观察下列算式:
...根据上述算式中的规律,你认为 ? ? ? 的末位数字是( ).
答案:C
? A. 2?
B. 4?
C. 6?
D. 8
,
,
,
,
,
,
,
观察下列算式:
?探究计算结果中的个位数字的规律,猜测? ? ? ? +1的个位数字是______.
答案:8
3的幂的末位数字规律
,
,
,
,
.
幂比大小
答案:C
? ? ? ? ?比 ? ? ? ? ? ? 小 (? ? ?).?
A. 2
B. -2
C.?
D .
总结
这节课我们学到了什么?
有理数混合运算的顺序
1. 先_______、再______、最后______.
2. 同级运算,从______到_____进行.
3. 如有括号,先做_________的运算,按小括号、中括号、大括号依次行.
乘方
乘除?
加减?
左?
右
括号内?
1、有理数的混合运算包含哪些运算?
2、有理数混合运算的顺序是什么?
3、有理数混合运算需要注意些什么?
有理数的混合运算
