山东省烟台市2020-2021学年高一下学期期末考试数学试题 Word版含答案
文档属性
| 名称 | 山东省烟台市2020-2021学年高一下学期期末考试数学试题 Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 657.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 22:00:48 | ||
图片预览




文档简介
烟台市2020-2021学年度第二学期期末学业水平诊断
高一数学
注意事项:
1.本试题满分150分,考试时间为120分钟。
2.使用答题纸时,必须使用0.5毫米的黑色签字笔书写,要字迹工整,笔迹清晰;超出答题区书写的答案无效;在草稿纸、试题卷上答题无效。
3.答卷前将密封线内的项目填写清楚。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若空间中两个角的两条边分别对应平行,则这两个角
A.相等 B.互补 C.相等或互补 D.不能确定
2.抛掷一枚质地均匀的正六面体骰子,其六个面分别标有数字1,2,3,4,5,6,观察朝上一面的点数,设事件false“点数为奇数”,false“点数为4”,则false与false的关系为
A.互斥 B.相等 C.互为对立 D.相互独立
3.已知一个水平放置的三角形的斜二测直观图的面积为1,那么原三角形的面积为
A.false B.2 C.false D.4
4.某学校采用分层随机抽样方法,抽取一定数量的高中学生参加安全知识竞赛.若得到的样本中高二的学生数量比高一多40人、比高三少20人,且全校高一、高三学生数之比为2:3,则样本容量为
A.120 B.160 C.180 D.460
5.某人有3把钥匙,其中仅有一把能打开门.如果他每次都随机选取-把钥匙开门,不能打开门时就扔掉,则他第二次才能打开门的概率为
A.false B.false C.false D.false
6.已知false,false表示两条不同的直线,false,false表示两个不同的平面,则
A.若false,false,则false B.若false,false,则false
C.若false,false,则false D.若false,false,则false
7.给定数据:10,12,17,25,50,75,则其第30百分位数、第50百分位数分别为
A.11,17 B.11,21 C.12,17 D.12,21
8.在右图所示的三棱锥容器false中,false,false,false分别为三条侧棱上的小洞,false,false,若用该容器盛水,则最多可盛水的体积是原三棱锥容器体积的
A.false B.false C.false D.false
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列说法正确的有
A.两条相交直线确定一个平面
B.平行于同一平面的两条直线平行
C.标准差刻画了一组数据的离散程度或波动幅度
D.若某种奖券的中奖率为0.1,则抽奖10次必有一次中奖
10.已知圆锥的底面半径为1,高为false,false为顶点,false,false为底面圆周上两个动点,则
A.圆锥的体积为false
B.圆锥的侧面展开图的圆心角大小为false
C.圆锥截面false的面积的最大值为false
D.从点false出发绕圆锥侧面一周回到点false的无弹性细绳的最短长度为false
11.在正方体false中,点false为线段false上一动点,则
A.对任意的点false,都有false
B.三棱锥false的体积为定值
C.当false为false中点时,异面直线false与false所成的角最小
D.当false为false、中点时,直线false与平面false所成的角最大
12.算盘是我国古代一项伟大的发明,是一类重要的计算工具.下图是一把算盘的初始状态,自右向左,分别表示个位、十位、百位、千位……,上面一粒珠子(简称上珠)代表5,下面一粒珠子(简称下珠)代表1,五粒下珠的大小等于同组一粒上珠的大小.例如,个位拨动一粒上珠、十位拨动一粒下珠至梁上,表示数字15.现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子至梁上,设事件false“表示的四位数能被3整除”,false表示的四位数能被5整除”,则
A.false B.false C.false D.false
三、填空题:本题共4小题,每小题5分,共20分。
13.甲、乙两人打靶,已知甲的命中率为0.8,乙的命中率为0.7,若甲、乙分别向同一靶子射击一次,则该靶子被击中的概率为______.
14.已知一个长方体共顶点的三个面的面积分别为2,3,4,则其体对角线长度为______.
15.类比是研究数学问题的重要方法之一.数学家波利亚曾说:“求解立体几何问题往往有赖于平面几何中的类比问题.”在平面几何里,研究三角形三边长度间的关系,有勾股定理:“设false的两边false,则false.”拓展到空间,类比研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥false的三个侧面false,false,false两两互相垂直,则______.
16.在三棱锥false中,面false面false,false,false,则该三棱锥外接球的表面积为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
如图,在空间四边形false中,false,false,false,false分别为棱false,false,false,false的中点.
(1)求证:四边形false为平行四边形;
(2)当对角线false与false满足什么条件时,四边形false为正方形?(给出一个满足题意的条件即可,不必证明).
18.(12分)
某快餐配送平台针对外卖员送餐准点情况制定了如下的考核方案:每一单自接单后在规定时间内送达、延迟5分钟内送达、延迟5至10分钟送达、其他延迟情况,分别评定为false,false,false,false四个等级,各等级依次奖励3元、奖励0元、罚款3元、罚款6元.假定评定为等级false,false,false的概率分别是false,false,false.
(1)若某外卖员接了一个订单,求其延迟送达且被罚款的概率;
(2)若某外卖员接了两个订单,且两个订单互不影响,求这两单获得的奖励之和为0元的概率.
19.(12分)
为调查高一、高二学生心理健康达标情况,某学校采用分层随机抽样方法,从高一、高二学生中分别抽取了50人、40人参加心理健康测试(满分:10分).经初步统计,参加测试的高-学生成绩falsefalse的平均分false,方差false,高二学生的成绩falsefalse的统计表如下:
成绩false
4
5
6
7
8
9
频数
3
7
11
9
6
4
(1)计算参加测试的高二学生成绩的平均分false和方差false;
(2)估计该学校高一、高二全体学生的平均分false和方差false.
20、(12分)
如图,在直三棱柱false中,false,false.
(1)求证:false;
(2)若false与平面false所成角的正弦值为false,求三棱锥false的体积.
21.(12分)
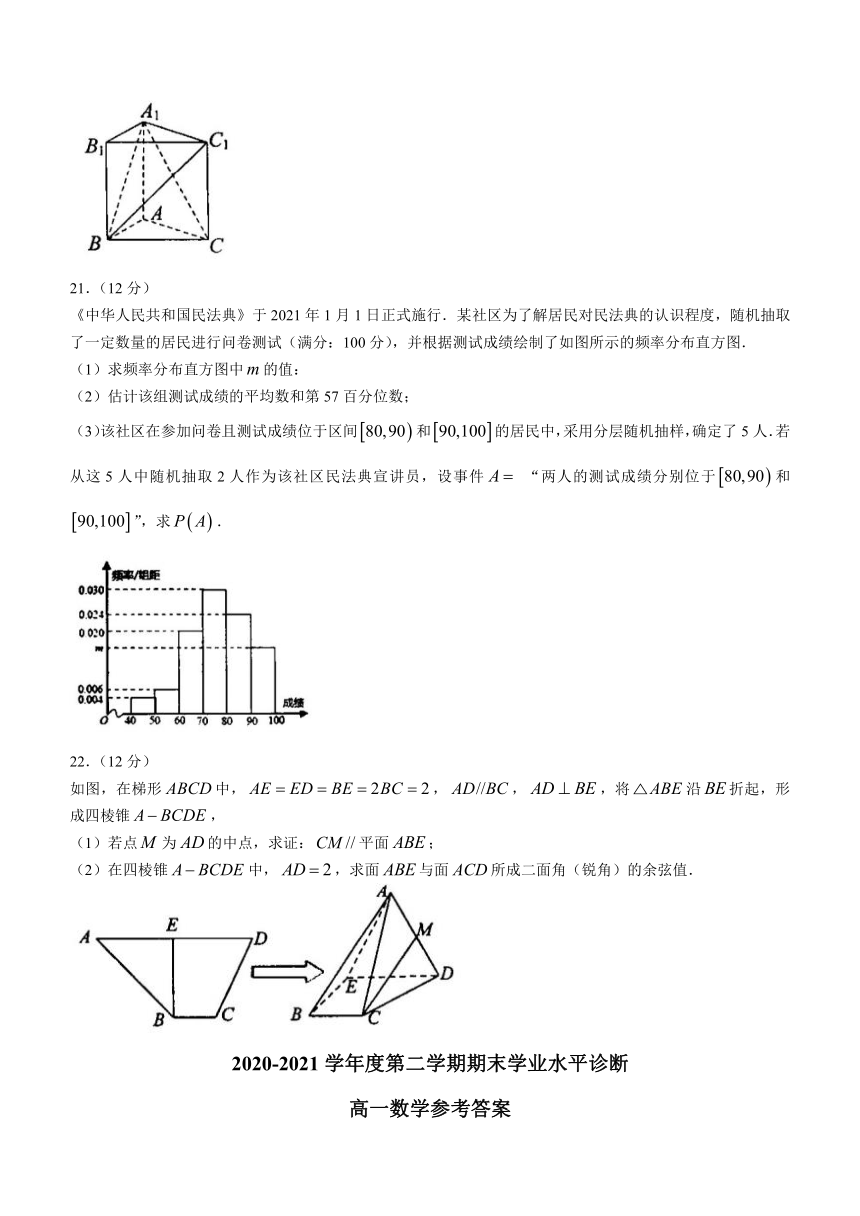
《中华人民共和国民法典》于2021年1月1日正式施行.某社区为了解居民对民法典的认识程度,随机抽取了一定数量的居民进行问卷测试(满分:100分),并根据测试成绩绘制了如图所示的频率分布直方图.
(1)求频率分布直方图中false的值:
(2)估计该组测试成绩的平均数和第57百分位数;
(3)该社区在参加问卷且测试成绩位于区间false和false的居民中,采用分层随机抽样,确定了5人.若从这5人中随机抽取2人作为该社区民法典宣讲员,设事件false “两人的测试成绩分别位于false和false”,求false.
22.(12分)
如图,在梯形false中,false,false,false,将false沿false折起,形成四棱锥false,
(1)若点false为false的中点,求证:false平面false;
(2)在四棱锥false中,false,求面false与面false所成二面角(锐角)的余弦值.
2020-2021学年度第二学期期末学业水平诊断
高一数学参考答案
一、选择题
C A C D B C D A
二、选择题
9.AC 10.BCD 11.ABD 12.ACD
三、填空题
13.0.94 14.false 15.false 16.false
四、解答题
17.证明:(1)连接false,因为false,false分别为棱false,false的中点,
所以false,false
同理false,false
所以false且false
所以四边形false是平行四边形.
(2)当false且false时,四边形false为正方形.
18.解:(1)设事件false,false,false,false分别表示“被评为等级false,false,false,false”.
由题意,事件false,false,false,false两两互斥,
所以false.
又false“延迟送达且被罚款”,
所以false.
因此“延迟送达且被罚款”的概率为false.
(2)设事件false,false,false,false表示“第false单被评为等级false,false,false,false”,false.
则“两单共获得的奖励为0元”即事件false,
且事件false,false,false互斥,
又false
又false
所以false
false
false
19.解:(1)由题意,
false
false.
false
false.
(2)由(1)可得,false
false
false
false.
20.解(1)证明:因为false,false,false
所以false平面false,
false平面false,所以false
又因为直三棱柱false中,false,
所以四边形false为正方形,所以false.
因为false,所以false平面false,
false平面false,所以false.
(2)过false作false,垂足为false,连false,则false平面false,
false为false与平面false所成的角.
因为false,则false,
所以false,所以false.
在false中,false,所以false.
在false中,false.
所以false.
21.解:(1)由己知false,
解得false.
(2)测试成绩的平均数
false
false.
测试成绩落在区间false的频率为false,
落在在区间false的频率为false,
所以设第57百分位数为false,有false,
解得false.
(3)由题知,测试分数位于区间false、false的人数之比为false,
所以采用分层随机抽样确定的5人,在区间false中3人,用false,false,false表示,在区间false中2人,用false,false表示.
从这5人中抽取2人的所有可能情况有:false,false,false,false,false,false,false,false,false,false,共10种.
其中“落在区间false和false”有6种.
所以false.
22.解:(1)证明:取false中点false,连false,则false,false.
又因为false,false,
所以false,false.
所以四边形false为平行四边形,所以false.
又因为false平面false,false平面false
所以false平面false.
(2)延长false,false交于点false,则false为平面false与平面false的交线
因为false,false,所以false.
三角形false中,因为false,false为false的中点,
所以false,
又因为false,false,false
所以false平面false,false平面false,
所以false.
又因为false,所以false平面false.
false平面false,所以false.
在三角形false中,过false作false,垂足为false,连接false,因为false.
所以false平面false,false平面false,所以false.
所以false为二面角false的平面角.
在false中,false,false,false,
由falsefalsefalse,所以false,false.
在false中,false,false,false.
所以false.
即面false与面false所成二面角(锐角)的余弦值为false.
高一数学
注意事项:
1.本试题满分150分,考试时间为120分钟。
2.使用答题纸时,必须使用0.5毫米的黑色签字笔书写,要字迹工整,笔迹清晰;超出答题区书写的答案无效;在草稿纸、试题卷上答题无效。
3.答卷前将密封线内的项目填写清楚。
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若空间中两个角的两条边分别对应平行,则这两个角
A.相等 B.互补 C.相等或互补 D.不能确定
2.抛掷一枚质地均匀的正六面体骰子,其六个面分别标有数字1,2,3,4,5,6,观察朝上一面的点数,设事件false“点数为奇数”,false“点数为4”,则false与false的关系为
A.互斥 B.相等 C.互为对立 D.相互独立
3.已知一个水平放置的三角形的斜二测直观图的面积为1,那么原三角形的面积为
A.false B.2 C.false D.4
4.某学校采用分层随机抽样方法,抽取一定数量的高中学生参加安全知识竞赛.若得到的样本中高二的学生数量比高一多40人、比高三少20人,且全校高一、高三学生数之比为2:3,则样本容量为
A.120 B.160 C.180 D.460
5.某人有3把钥匙,其中仅有一把能打开门.如果他每次都随机选取-把钥匙开门,不能打开门时就扔掉,则他第二次才能打开门的概率为
A.false B.false C.false D.false
6.已知false,false表示两条不同的直线,false,false表示两个不同的平面,则
A.若false,false,则false B.若false,false,则false
C.若false,false,则false D.若false,false,则false
7.给定数据:10,12,17,25,50,75,则其第30百分位数、第50百分位数分别为
A.11,17 B.11,21 C.12,17 D.12,21
8.在右图所示的三棱锥容器false中,false,false,false分别为三条侧棱上的小洞,false,false,若用该容器盛水,则最多可盛水的体积是原三棱锥容器体积的
A.false B.false C.false D.false
二、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分。
9.下列说法正确的有
A.两条相交直线确定一个平面
B.平行于同一平面的两条直线平行
C.标准差刻画了一组数据的离散程度或波动幅度
D.若某种奖券的中奖率为0.1,则抽奖10次必有一次中奖
10.已知圆锥的底面半径为1,高为false,false为顶点,false,false为底面圆周上两个动点,则
A.圆锥的体积为false
B.圆锥的侧面展开图的圆心角大小为false
C.圆锥截面false的面积的最大值为false
D.从点false出发绕圆锥侧面一周回到点false的无弹性细绳的最短长度为false
11.在正方体false中,点false为线段false上一动点,则
A.对任意的点false,都有false
B.三棱锥false的体积为定值
C.当false为false中点时,异面直线false与false所成的角最小
D.当false为false、中点时,直线false与平面false所成的角最大
12.算盘是我国古代一项伟大的发明,是一类重要的计算工具.下图是一把算盘的初始状态,自右向左,分别表示个位、十位、百位、千位……,上面一粒珠子(简称上珠)代表5,下面一粒珠子(简称下珠)代表1,五粒下珠的大小等于同组一粒上珠的大小.例如,个位拨动一粒上珠、十位拨动一粒下珠至梁上,表示数字15.现将算盘的个位、十位、百位、千位分别随机拨动一粒珠子至梁上,设事件false“表示的四位数能被3整除”,false表示的四位数能被5整除”,则
A.false B.false C.false D.false
三、填空题:本题共4小题,每小题5分,共20分。
13.甲、乙两人打靶,已知甲的命中率为0.8,乙的命中率为0.7,若甲、乙分别向同一靶子射击一次,则该靶子被击中的概率为______.
14.已知一个长方体共顶点的三个面的面积分别为2,3,4,则其体对角线长度为______.
15.类比是研究数学问题的重要方法之一.数学家波利亚曾说:“求解立体几何问题往往有赖于平面几何中的类比问题.”在平面几何里,研究三角形三边长度间的关系,有勾股定理:“设false的两边false,则false.”拓展到空间,类比研究三棱锥的侧面面积与底面面积间的关系,可以得出的正确结论是:“设三棱锥false的三个侧面false,false,false两两互相垂直,则______.
16.在三棱锥false中,面false面false,false,false,则该三棱锥外接球的表面积为______.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)
如图,在空间四边形false中,false,false,false,false分别为棱false,false,false,false的中点.
(1)求证:四边形false为平行四边形;
(2)当对角线false与false满足什么条件时,四边形false为正方形?(给出一个满足题意的条件即可,不必证明).
18.(12分)
某快餐配送平台针对外卖员送餐准点情况制定了如下的考核方案:每一单自接单后在规定时间内送达、延迟5分钟内送达、延迟5至10分钟送达、其他延迟情况,分别评定为false,false,false,false四个等级,各等级依次奖励3元、奖励0元、罚款3元、罚款6元.假定评定为等级false,false,false的概率分别是false,false,false.
(1)若某外卖员接了一个订单,求其延迟送达且被罚款的概率;
(2)若某外卖员接了两个订单,且两个订单互不影响,求这两单获得的奖励之和为0元的概率.
19.(12分)
为调查高一、高二学生心理健康达标情况,某学校采用分层随机抽样方法,从高一、高二学生中分别抽取了50人、40人参加心理健康测试(满分:10分).经初步统计,参加测试的高-学生成绩falsefalse的平均分false,方差false,高二学生的成绩falsefalse的统计表如下:
成绩false
4
5
6
7
8
9
频数
3
7
11
9
6
4
(1)计算参加测试的高二学生成绩的平均分false和方差false;
(2)估计该学校高一、高二全体学生的平均分false和方差false.
20、(12分)
如图,在直三棱柱false中,false,false.
(1)求证:false;
(2)若false与平面false所成角的正弦值为false,求三棱锥false的体积.
21.(12分)
《中华人民共和国民法典》于2021年1月1日正式施行.某社区为了解居民对民法典的认识程度,随机抽取了一定数量的居民进行问卷测试(满分:100分),并根据测试成绩绘制了如图所示的频率分布直方图.
(1)求频率分布直方图中false的值:
(2)估计该组测试成绩的平均数和第57百分位数;
(3)该社区在参加问卷且测试成绩位于区间false和false的居民中,采用分层随机抽样,确定了5人.若从这5人中随机抽取2人作为该社区民法典宣讲员,设事件false “两人的测试成绩分别位于false和false”,求false.
22.(12分)
如图,在梯形false中,false,false,false,将false沿false折起,形成四棱锥false,
(1)若点false为false的中点,求证:false平面false;
(2)在四棱锥false中,false,求面false与面false所成二面角(锐角)的余弦值.
2020-2021学年度第二学期期末学业水平诊断
高一数学参考答案
一、选择题
C A C D B C D A
二、选择题
9.AC 10.BCD 11.ABD 12.ACD
三、填空题
13.0.94 14.false 15.false 16.false
四、解答题
17.证明:(1)连接false,因为false,false分别为棱false,false的中点,
所以false,false
同理false,false
所以false且false
所以四边形false是平行四边形.
(2)当false且false时,四边形false为正方形.
18.解:(1)设事件false,false,false,false分别表示“被评为等级false,false,false,false”.
由题意,事件false,false,false,false两两互斥,
所以false.
又false“延迟送达且被罚款”,
所以false.
因此“延迟送达且被罚款”的概率为false.
(2)设事件false,false,false,false表示“第false单被评为等级false,false,false,false”,false.
则“两单共获得的奖励为0元”即事件false,
且事件false,false,false互斥,
又false
又false
所以false
false
false
19.解:(1)由题意,
false
false.
false
false.
(2)由(1)可得,false
false
false
false.
20.解(1)证明:因为false,false,false
所以false平面false,
false平面false,所以false
又因为直三棱柱false中,false,
所以四边形false为正方形,所以false.
因为false,所以false平面false,
false平面false,所以false.
(2)过false作false,垂足为false,连false,则false平面false,
false为false与平面false所成的角.
因为false,则false,
所以false,所以false.
在false中,false,所以false.
在false中,false.
所以false.
21.解:(1)由己知false,
解得false.
(2)测试成绩的平均数
false
false.
测试成绩落在区间false的频率为false,
落在在区间false的频率为false,
所以设第57百分位数为false,有false,
解得false.
(3)由题知,测试分数位于区间false、false的人数之比为false,
所以采用分层随机抽样确定的5人,在区间false中3人,用false,false,false表示,在区间false中2人,用false,false表示.
从这5人中抽取2人的所有可能情况有:false,false,false,false,false,false,false,false,false,false,共10种.
其中“落在区间false和false”有6种.
所以false.
22.解:(1)证明:取false中点false,连false,则false,false.
又因为false,false,
所以false,false.
所以四边形false为平行四边形,所以false.
又因为false平面false,false平面false
所以false平面false.
(2)延长false,false交于点false,则false为平面false与平面false的交线
因为false,false,所以false.
三角形false中,因为false,false为false的中点,
所以false,
又因为false,false,false
所以false平面false,false平面false,
所以false.
又因为false,所以false平面false.
false平面false,所以false.
在三角形false中,过false作false,垂足为false,连接false,因为false.
所以false平面false,false平面false,所以false.
所以false为二面角false的平面角.
在false中,false,false,false,
由falsefalsefalse,所以false,false.
在false中,false,false,false.
所以false.
即面false与面false所成二面角(锐角)的余弦值为false.
同课章节目录
