人教版高中物理选修2-2 3.1 常见的传动装置 同步测试(含解析)
文档属性
| 名称 | 人教版高中物理选修2-2 3.1 常见的传动装置 同步测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 206.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-07-09 15:24:08 | ||
图片预览




文档简介
人教版高中物理选修2-2第三章第一节 常见的传动装置 同步测试
一、单选题(共10题;共20分)
1.如图所示,一个质量为m的人站在台秤上,跨过光滑定滑轮将质量为m′的重物从高处放下,设重物以加速度a加速下降(a<g),且m′<m , 则台秤上的示数为( )
A.?(m+m′)g﹣m′a??????????B.?(m﹣m′)g+m′a??????????C.?(m﹣m′)g﹣m′a??????????D.?(m﹣m′)g
2.如图所示,“┏”型均匀杆的总长为3L,在竖直平面内可绕光滑的水平轴O转动.若在右端A施加一个竖直向下的力F,使杆顺时针缓慢转动,则在杆AB从水平到转过45°的过程中,以下说法中正确的是( )
A.?力F的力矩变大??????B.?力F的力矩先变大后变小??????C.?力F的大小不变??????D.?力F的大小先变大后变小
3.如图所示,三根横截面完全相同的圆木材A、B、C按图示方法放在水平面上,它们均处于静止状态,则下列说法正确的是( )
A.?B、C所受的合力大于A受的合力?????????????????????B.?B、C对A的作用力的合力方向竖直向上
C.?B与C之间一定存在弹力??????????????????????????????????D.?如果水平面光滑,则它们仍有可能保持图示的平衡
4.根据汉族民间传说,木杆秤是鲁班发明的.它是我国民间过去很长时间一直使用的称量物体质量的衡器.通常它是由一根一头粗、一头细的质量分布不均匀的直杆、称钩(BD)、提纽(O)、用可左右移动的轻线悬挂的称砣(质量为m)组成.称杆与称钩整体的重心在C点.不称物体时,将称砣置于A处,此时手提提纽,称杆恰能水平平衡.因而A点质量的刻度为零.当称钩上悬挂重物时,秤砣向右移动x到P点时重新平衡.则下列有关说法正确的是( )
A.?杆秤上的刻度一定是均匀的
B.?其它条件不变,OB之间的距离越小,称量范围越小
C.?其它条件不变,砣的质量越大,秤量范围越小
D.?如果在加速上升的电梯中,杆秤称量计数将偏大
5.如图所示为等刻度的轻质杠杆,A处挂一个重为2牛的物体,若要使杠杆在水平位置平衡,则在B处施加的力( )
A.?可能是0.5牛????????????????????????B.?一定是1牛????????????????????????C.?可能是2牛????????????????????????D.?一定是4牛
6.如图所示,质量不均匀的直木棒以左端为轴,在力F的作用下,由水平位置缓慢的拉到图中虚线位置.在此过程中力F始终保持与棒垂直,以下说法中正确的是( )
A.?力F变小,其力矩变小?????????????????????????????????????????B.?力F变大,其力矩变大
C.?力F不变,其力矩也不变??????????????????????????????????????D.?力F不变,其力矩变小
7.如图所示,AC是上端带定滑轮的固定竖直杆,质量不计的轻杆AB一端通过铰链固定在A点,另一端B悬挂一重为G的物体,且B端系有一根轻绳并绕过定滑轮C , 用力F拉绳,开始时∠BAC>90° , 现使∠BAC缓慢变小,直到杆AB接近竖直杆AC . 此过程中,轻杆B端所受的力( )
A.?逐渐减小?????????????????????????B.?逐渐增大?????????????????????????C.?大小不变?????????????????????????D.?先减小后增大
8.下列关于使用机械的说法,错误的是( )
A.?实际情况下,使用机械总是费功的??????????????????????B.?不管什么情况下,使用机械都不可能省功
C.?使用机械一定可以省力???????????????????????????????????????D.?使用机械可能更费力
9.如图所示,abc为质量均匀的直角等边曲杆,曲杆可绕c端的光滑铰链,在竖直平面内转动.若在a端施加力F1和F2 , 根据图象所示方向,我们可以得到的结论正确的是( )
A.?F1和F2都产生顺时针效果的力矩
B.?F1产生顺时针效果的力矩,F2产生逆时针效果的力矩
C.?F1产生逆时针效果的力矩,F2顺时针效果的力矩
D.?F1和F2都产生逆时针效果的力矩
10.如图所示,两个质量为m1的小球套在竖直放置的光滑支架上,支架的夹角为120°,用轻绳将两球与质量为m2的小球连接,绳与杆构成一个菱形,则m1:m2为( )
A.?1:1?????????????????????????????????B.?1:2?????????????????????????????????C.?1: ?????????????????????????????????D.?:2
二、填空题(共4题;共8分)
11.如图,粗细均匀的均质杆AB在B点用铰链与竖直墙连接,杆长为L . A端有一轻质滑轮(大小可忽略).足够长的轻绳通过滑轮将重物吊住.若θ为370时恰好达到平衡,且保持绳AC在水平方向,则杆AB的质量m与重物的质量M的比值为________.若将杆换为长度不变的轻杆,其它条件不变,则系统平衡时轻杆与竖直墙面的夹角为________.(sin37°=0.6,cos37°=0.8)
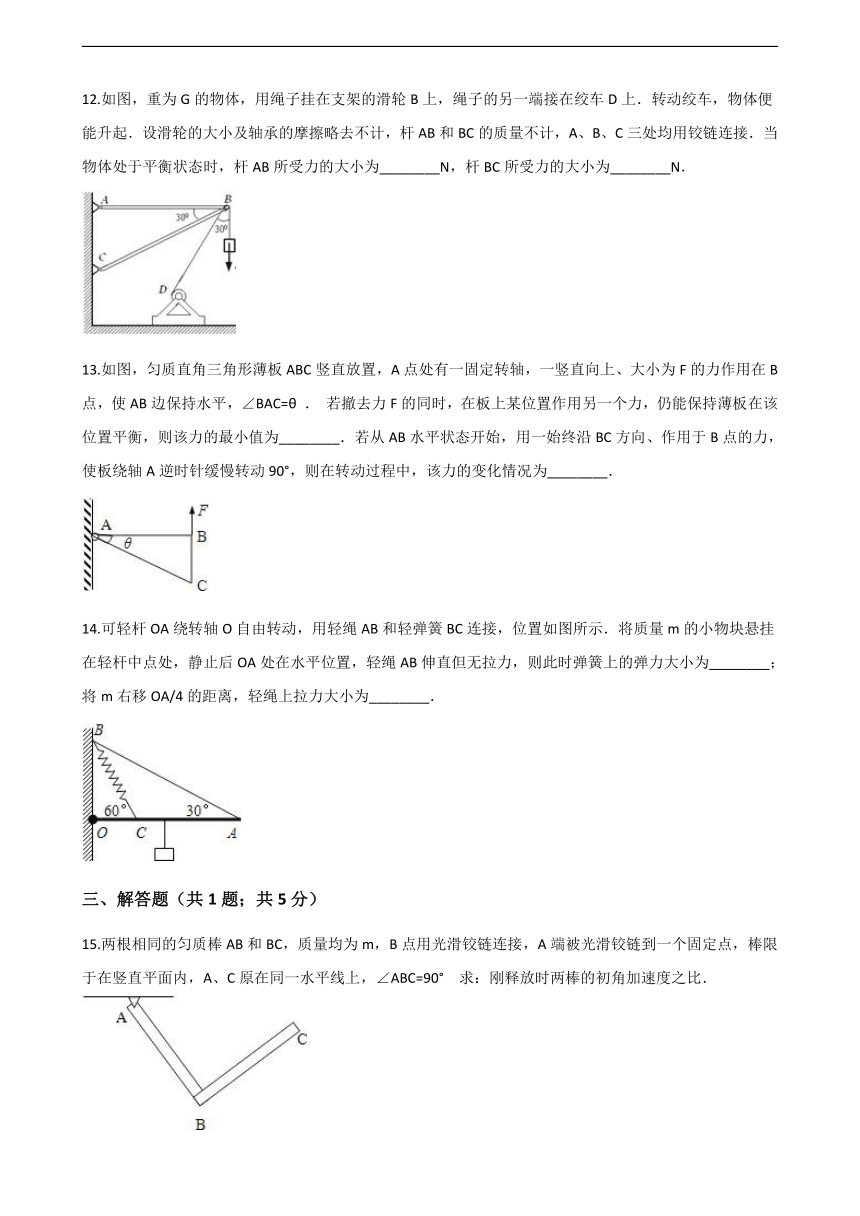
12.如图,重为G的物体,用绳子挂在支架的滑轮B上,绳子的另一端接在绞车D上.转动绞车,物体便能升起.设滑轮的大小及轴承的摩擦略去不计,杆AB和BC的质量不计,A、B、C三处均用铰链连接.当物体处于平衡状态时,杆AB所受力的大小为________N,杆BC所受力的大小为________N.
13.如图,匀质直角三角形薄板ABC竖直放置,A点处有一固定转轴,一竖直向上、大小为F的力作用在B点,使AB边保持水平,∠BAC=θ . 若撤去力F的同时,在板上某位置作用另一个力,仍能保持薄板在该位置平衡,则该力的最小值为________.若从AB水平状态开始,用一始终沿BC方向、作用于B点的力,使板绕轴A逆时针缓慢转动90°,则在转动过程中,该力的变化情况为________.
14.可轻杆OA绕转轴O自由转动,用轻绳AB和轻弹簧BC连接,位置如图所示.将质量m的小物块悬挂在轻杆中点处,静止后OA处在水平位置,轻绳AB伸直但无拉力,则此时弹簧上的弹力大小为________;将m右移OA/4的距离,轻绳上拉力大小为________.
三、解答题(共1题;共5分)
15.两根相同的匀质棒AB和BC,质量均为m,B点用光滑铰链连接,A端被光滑铰链到一个固定点,棒限于在竖直平面内,A、C原在同一水平线上,∠ABC=90° 求:刚释放时两棒的初角加速度之比.
四、综合题(共2题;共20分)
16.利用钓鱼竿钓鱼的示意图如图所示,O为支点,F1是手对鱼竿的作用力,请画出:
?
(1)鱼线对钓鱼竿拉力F2的示意图;
(2)F1的力臂.
17.如图所示,一质量为M=2kg的铁块套在倾斜放置的杆上,杆与水平方向的夹角θ=60°,一轻绳一端连在铁块上,一端连在一质量为m=1kg的小球上,一水平力F作用在小球上,连接铁块与球的轻绳与杆垂直,铁块和球都处于静止状态.(g取10m/s2)求:
(1)?拉力F的大小;
(2)杆对铁块的摩擦力的大小.
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】对重物受力分析,受重力和拉力,加速下降,根据牛顿第二定律,有:m′g﹣T=m′a①再对人受力分析,受到重力、拉力和支持力,根据共点力平衡条件,有:N+T=mg ②
由①②,解得
N=(m﹣m′)g+m′a
故选B.
【分析】先对重物受力分析,受重力和拉力,加速下降,然后根据牛顿第二定律列式求出绳子的拉力;再对人受力分析,受到重力、拉力和支持力,根据平衡条件求出支持力,而台秤读数等于支持力.
2.【答案】B
【解析】【解答】解:设杆转动α角,“┏”型均匀杆的总质量为m,力F的力矩等于BC段重力的力矩,根据力矩平衡条件,有: ( mg)?x=F?Lcosα;(x为BC段的中点与O点连线的水平分量)
由于x先变大后变小,故( mg)?x先变大后变小,F?Lcosα先变大后变小,故ACD错误,B正确;
故选:B.
【分析】BO段与AO段的重力的力矩恰好平衡,故拉力的力矩等于BC段重力的力矩,然后根据力矩平衡条件列式分析.
3.【答案】B
【解析】【解答】A、由题意可知,三个小球均处于静止状态,故各物体所受合力都为零,故合力相等,故A错误;B、对A受力分析可知,A受重力和BC的支持力而处于平衡,故BC对A的作用力的合力方向竖直同上,故B正确;
C、对B受力分析,B受重力、支持力、A的弹力及地面的摩擦力,若这些力能使物体平衡,则BC间没有弹力,故C错误;
D、若圆柱体光滑,则下面的两物体BC将不能保持静止,故D错误;
故选:B.
【分析】对物体进行受力分析,由共点力的平衡条件可知它们受到的合力均为零;用假设法可得出圆柱体光滑时能否平衡.
4.【答案】A
【解析】解答:A、由图可知,OA之间的距离为a , OB之间的距离为b , OC之间的距离为c , 设OB杆的质量为m0 , 秤砣与A之间的距离为x , 当秤砣在A点到达平衡时:m0g?c=(m+m′)g?a ①
当秤砣在距离A点的距离为x到达平衡时.得:
m0g?c+Mg?b=m′ga+mg(a+x)
联立以上二式得:M?b=m?x ②
即,重物的质量与秤砣到A点的距离成正比,所以杆秤上的刻度一定是均匀的.故A正确;
B、由②式可知, ,其它条件不变,OB之间的距离b越小,称量的质量的范围越大.故B错误;
C、由②式可知, ,其它条件不变,砣的质量越大,秤量范围越大.故C错误;
D、若在加速上升的电梯中,设加速度大小为:a0 , 当秤砣在距离A点的距离为x到达平衡时.得:
m0(g+a0)?c+M(g+a0)?b=m′(g+a0)?a+m(g+a0)(a+x)
整理得:M?b=m?x , 可知与电梯的加速度无关.所以如果在加速上升的电梯中,杆秤称量计数不变.
故D错误.
故选:A
分析:杆秤利用杠杆的平衡条件,通过力臂的大小关系得出物体的质量与秤砣的质量之间的关系,测量物体的质量.该题根据该原理解答即可.
5.【答案】C
【解析】【解答】解:设杠杆每一格长度是L, 当B处的作用力与杠杆垂直时,力臂最大,此时作用力最小,
由杠杆平衡条件可得:FALA=FB最小LB , 即:2N×2L=FB最小×4L,
则FB最小=1N,当作用在B处的力与杠杆不垂直时,力臂小于4L,
作用力大于1N,因此要使杠杆平衡,作用在B处的力F≥1N,故ABD错误,C正确;
故选C.
【分析】根据杠杆平衡的条件和杠杆中最小力的问题进行分析,即动力乘以动力臂等于阻力乘以阻力臂,支点与力的作用点的连线为最长力臂.
6.【答案】D
【解析】【解答】解:对木棒分析可知,以左侧为支点,木棒受重力和F的作用下处于力矩平衡状态,故力F的力矩与重力力矩平衡;则有:mgL=FL′ 在移动过程中,重力不变,重力力臂减小,故重力的力矩减小,根据力矩平衡可知,力F的力矩减小;
由图可知,重力力臂和F的力臂之比恒定,故F保持不变;
故D正确,ABC错误.
故选:D.
【分析】木棒在重力和拉力作用下处于平衡状态,分别明确二者的力臂,再根据力矩平衡条件即可分析力矩与力的变化情况.
7.【答案】C
【解析】【解答】A、由于B点始终处于平衡状态,故B点受到的力的大小为各力的合力.故B点在变化过程中受到的力始终为0.故大小不变.故A错误B、由对A项的分析知B点受到的力始终为0,不变.故B错误.
C、由对A项的分析知B点受到的力始终为0,不变.故C正确.
D、由对A项的分析知B点受到的力始终为0,不变.故D错误.
故选:C
【分析】以B为研究对象,并受力分析.由题目中“缓慢”二字知整个变化过程中B处于平衡态.
8.【答案】C
【解析】【解答】A、不管什么情况下,使用任何机械都不会省功;实际情况下,考虑机械的摩擦,使用机械总是费功的,故A正确,B正确;
C、D、根据公式W=FS , 省力的费距离,费力的省距离,故C错误,D正确;
本题选择错误的,故选:C.
【分析】解决此题的关键是知道使用任何机械都不会省功,省力的费距离,费力的省距离.
9.【答案】A
【解析】【解答】解:先将力的作用点与支点连接起来,如图所示:
假设只有拉力F1作用,杆会顺时针转动;
假设只有拉力F2作用,杆同样会顺时针转动;
故F1和F2都产生顺时针效果的力矩;
故选:A.
【分析】先将c端与a端用直线连接起来,然后考虑拉力F1与F2的力矩是顺时针效果还是逆时针效果.
10.【答案】A
【解析】解答:将小球m2的重力按效果根据平行四边形定则进行分解如图,
由几何知识得:T=m2g ①
对m1受力分析,由平衡条件,在沿杆的方向有:m1gsin30°=Tsin30°
得:T=m1g ②
可见m1:m2的=1:1;
故选:A.
分析:将小球m2的重力按效果根据平行四边形定则进行分解,由几何知识求出m2g与绳子拉力T的关系,对m1受力分析,由平衡条件求出m1g与T的关系,进而得到m1:m2的比值.
二、填空题
11.【答案】;aRccos
【解析】【解答】由于物体m受力平衡,故细线的拉力等于mg;
当若θ为37°时杆恰好达到平衡,以B为支点,设杆长为L , 根据力矩平衡条件得:
sin37°+MgLsin37°=MgLcos37°
解得:m:M=2:3
设AB长为L , 这BC为0.8L;
若将杆换为长度不变的轻杆,杆AB受到铰链的作用力和轻绳对AB的压力,要使杆能够平衡,轻绳对AB的压力方向应在AC与AB之间,而轻绳对AB的压力等于轻绳AC和AG拉力的合力,这两个拉力大小相等,故AB在细线的两侧拉力的角平分线上,如图所示:
故 , 则α=aRccos
故答案为: ,aRccos.
【分析】对粗细均匀的均质杆AB分析受力情况,若θ为37°时恰好达到平衡,以B为支点,根据力矩平衡条件求解质量之比;若将杆换为长度不变的轻杆,轻绳对AB的压力方向沿着杆的方向,即可得到θ的大小.
12.【答案】2.73G;3.73G
【解析】【解答】以A为支点,AB受到BC的支持力和两个绳子的拉力,它们的力臂如图1,设AB杆的长度为L , 则:
竖直向下的拉力的力臂;L1=L
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL1+GL2=FBC?L3
代入数据得:FBC=3.73G
同理,以C为支点,BC受到AB的拉力和两个绳子的拉力,它们的力臂如图2,则:
竖直向下的拉力的力臂: ;
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL4+GL5=FAB?L6
代入数据得:FAB=2.73G
故答案为:2.73G;3.73G
【分析】画出各个力,分别作出各个力的力臂,然后又力矩的平衡即可解答.
13.【答案】Fcosθ;先变大后变小
【解析】【解答】一竖直向上、大小为F的力作用在B点,使AB边保持水平,根据力矩平衡条件,有:
F?AB=G?d ①
(其中d为重力的力臂)
当力臂最大时,作用力最小,即F作用在C点,且与AC垂直,此时力臂最大,作用力最小,有:
F′?AC=G?d ②
联立①②两式,解得:
F′=Fcosθ
若从AB水平状态开始,用一始终沿BC方向、作用于B点的力,使板绕轴A逆时针缓慢转动90°,由于重力的力臂先增加后减小,拉力的力臂一直减小,根据力矩平衡条件,拉力先变大后变小;
故答案为:Fcosθ , 先变大后变小.
【分析】当作用力的力臂最大时,作用力最小;沿垂直AC方向、作用于C点的力最小;根据力矩平衡条件列式判断拉力的变化情况.
14.【答案】;
【解析】【解答】设OA长为l , 当绳无拉力,则弹簧的拉力的力矩与重力的力矩平衡,即:Flocsin60°=mg;
当m右移 的距离时,由力矩平衡得:Flocsin60°+Tlsin30°=mg;
解得:F= ,T=
答案为: ,
【分析】杠杆平衡的条件:动力乘以动力臂等于阻力乘以阻力臂;如图所示,根据直角三角形角与边的关系,求出绳子对杠杆拉力的力臂;再利用已知的重力和重力的力臂以及杠杆平衡的条件求出拉力F的大小.
三、解答题
15.【答案】解:作出两匀质棒AB和BC的重力及力臂如图所示,设棒长为L 将两棒的重力进行分解如图所示
对AB棒有使棒转动的合力F1=mgsin45°+mgsin45°=
切向加速度a1=
角加速度
对BC棒有使棒转动的合力F2=mgsin45°=
切向加速度a2=
角加速度
则刚释放时两棒的初角加速度之比为
答:刚释放时两棒的初角加速度之比为 .
【解析】【分析】先明确两棒的转动过程,作出受到的重力并分解,再计算出切向加速度,再计算出角加速度.
四、综合题
16.【答案】(1)
(2)
【解析】【解答】(1)过拉力作用点作竖直向下的拉力F2(2)过支点O作F1作用线的垂线段(即动力臂L1).
如图所示
【分析】(1)拉力F2的作用点为鱼线与杆的交点,阻力的方向沿绳子向下,过拉力F2的作用点表示出拉力的方向;(2)已知支点和动力的方向,根据力臂的定义过支点作力的作用线的垂线.
17.【答案】(1)对B球受力,如图:
根据力的平衡条件,有:
水平方向:Tsinθ=F
竖直方向:Tcosθ=mg
故:
F=mgtanθ
解得:
F=10 N
(2)由于绳对铁块的拉力垂直于铁块,且铁块处于静止状态,因此铁块受到的摩擦力等于铁块的重力沿斜面向下的分力,即:
【解析】【解答】(1)对B球受力,如图:
根据力的平衡条件,有:
水平方向:Tsinθ=F
竖直方向:Tcosθ=mg
故:
F=mgtanθ
解得:
F=10 N(2)由于绳对铁块的拉力垂直于铁块,且铁块处于静止状态,因此铁块受到的摩擦力等于铁块的重力沿斜面向下的分力,即:
【分析】(1)对B球受力分析,受重力、拉力F和细线的拉力T , 根据平衡条件列式求解即可;(2)铁块受重力、细线的拉力和静摩擦力,根据平衡条件列式求解.
一、单选题(共10题;共20分)
1.如图所示,一个质量为m的人站在台秤上,跨过光滑定滑轮将质量为m′的重物从高处放下,设重物以加速度a加速下降(a<g),且m′<m , 则台秤上的示数为( )
A.?(m+m′)g﹣m′a??????????B.?(m﹣m′)g+m′a??????????C.?(m﹣m′)g﹣m′a??????????D.?(m﹣m′)g
2.如图所示,“┏”型均匀杆的总长为3L,在竖直平面内可绕光滑的水平轴O转动.若在右端A施加一个竖直向下的力F,使杆顺时针缓慢转动,则在杆AB从水平到转过45°的过程中,以下说法中正确的是( )
A.?力F的力矩变大??????B.?力F的力矩先变大后变小??????C.?力F的大小不变??????D.?力F的大小先变大后变小
3.如图所示,三根横截面完全相同的圆木材A、B、C按图示方法放在水平面上,它们均处于静止状态,则下列说法正确的是( )
A.?B、C所受的合力大于A受的合力?????????????????????B.?B、C对A的作用力的合力方向竖直向上
C.?B与C之间一定存在弹力??????????????????????????????????D.?如果水平面光滑,则它们仍有可能保持图示的平衡
4.根据汉族民间传说,木杆秤是鲁班发明的.它是我国民间过去很长时间一直使用的称量物体质量的衡器.通常它是由一根一头粗、一头细的质量分布不均匀的直杆、称钩(BD)、提纽(O)、用可左右移动的轻线悬挂的称砣(质量为m)组成.称杆与称钩整体的重心在C点.不称物体时,将称砣置于A处,此时手提提纽,称杆恰能水平平衡.因而A点质量的刻度为零.当称钩上悬挂重物时,秤砣向右移动x到P点时重新平衡.则下列有关说法正确的是( )
A.?杆秤上的刻度一定是均匀的
B.?其它条件不变,OB之间的距离越小,称量范围越小
C.?其它条件不变,砣的质量越大,秤量范围越小
D.?如果在加速上升的电梯中,杆秤称量计数将偏大
5.如图所示为等刻度的轻质杠杆,A处挂一个重为2牛的物体,若要使杠杆在水平位置平衡,则在B处施加的力( )
A.?可能是0.5牛????????????????????????B.?一定是1牛????????????????????????C.?可能是2牛????????????????????????D.?一定是4牛
6.如图所示,质量不均匀的直木棒以左端为轴,在力F的作用下,由水平位置缓慢的拉到图中虚线位置.在此过程中力F始终保持与棒垂直,以下说法中正确的是( )
A.?力F变小,其力矩变小?????????????????????????????????????????B.?力F变大,其力矩变大
C.?力F不变,其力矩也不变??????????????????????????????????????D.?力F不变,其力矩变小
7.如图所示,AC是上端带定滑轮的固定竖直杆,质量不计的轻杆AB一端通过铰链固定在A点,另一端B悬挂一重为G的物体,且B端系有一根轻绳并绕过定滑轮C , 用力F拉绳,开始时∠BAC>90° , 现使∠BAC缓慢变小,直到杆AB接近竖直杆AC . 此过程中,轻杆B端所受的力( )
A.?逐渐减小?????????????????????????B.?逐渐增大?????????????????????????C.?大小不变?????????????????????????D.?先减小后增大
8.下列关于使用机械的说法,错误的是( )
A.?实际情况下,使用机械总是费功的??????????????????????B.?不管什么情况下,使用机械都不可能省功
C.?使用机械一定可以省力???????????????????????????????????????D.?使用机械可能更费力
9.如图所示,abc为质量均匀的直角等边曲杆,曲杆可绕c端的光滑铰链,在竖直平面内转动.若在a端施加力F1和F2 , 根据图象所示方向,我们可以得到的结论正确的是( )
A.?F1和F2都产生顺时针效果的力矩
B.?F1产生顺时针效果的力矩,F2产生逆时针效果的力矩
C.?F1产生逆时针效果的力矩,F2顺时针效果的力矩
D.?F1和F2都产生逆时针效果的力矩
10.如图所示,两个质量为m1的小球套在竖直放置的光滑支架上,支架的夹角为120°,用轻绳将两球与质量为m2的小球连接,绳与杆构成一个菱形,则m1:m2为( )
A.?1:1?????????????????????????????????B.?1:2?????????????????????????????????C.?1: ?????????????????????????????????D.?:2
二、填空题(共4题;共8分)
11.如图,粗细均匀的均质杆AB在B点用铰链与竖直墙连接,杆长为L . A端有一轻质滑轮(大小可忽略).足够长的轻绳通过滑轮将重物吊住.若θ为370时恰好达到平衡,且保持绳AC在水平方向,则杆AB的质量m与重物的质量M的比值为________.若将杆换为长度不变的轻杆,其它条件不变,则系统平衡时轻杆与竖直墙面的夹角为________.(sin37°=0.6,cos37°=0.8)
12.如图,重为G的物体,用绳子挂在支架的滑轮B上,绳子的另一端接在绞车D上.转动绞车,物体便能升起.设滑轮的大小及轴承的摩擦略去不计,杆AB和BC的质量不计,A、B、C三处均用铰链连接.当物体处于平衡状态时,杆AB所受力的大小为________N,杆BC所受力的大小为________N.
13.如图,匀质直角三角形薄板ABC竖直放置,A点处有一固定转轴,一竖直向上、大小为F的力作用在B点,使AB边保持水平,∠BAC=θ . 若撤去力F的同时,在板上某位置作用另一个力,仍能保持薄板在该位置平衡,则该力的最小值为________.若从AB水平状态开始,用一始终沿BC方向、作用于B点的力,使板绕轴A逆时针缓慢转动90°,则在转动过程中,该力的变化情况为________.
14.可轻杆OA绕转轴O自由转动,用轻绳AB和轻弹簧BC连接,位置如图所示.将质量m的小物块悬挂在轻杆中点处,静止后OA处在水平位置,轻绳AB伸直但无拉力,则此时弹簧上的弹力大小为________;将m右移OA/4的距离,轻绳上拉力大小为________.
三、解答题(共1题;共5分)
15.两根相同的匀质棒AB和BC,质量均为m,B点用光滑铰链连接,A端被光滑铰链到一个固定点,棒限于在竖直平面内,A、C原在同一水平线上,∠ABC=90° 求:刚释放时两棒的初角加速度之比.
四、综合题(共2题;共20分)
16.利用钓鱼竿钓鱼的示意图如图所示,O为支点,F1是手对鱼竿的作用力,请画出:
?
(1)鱼线对钓鱼竿拉力F2的示意图;
(2)F1的力臂.
17.如图所示,一质量为M=2kg的铁块套在倾斜放置的杆上,杆与水平方向的夹角θ=60°,一轻绳一端连在铁块上,一端连在一质量为m=1kg的小球上,一水平力F作用在小球上,连接铁块与球的轻绳与杆垂直,铁块和球都处于静止状态.(g取10m/s2)求:
(1)?拉力F的大小;
(2)杆对铁块的摩擦力的大小.
答案解析部分
一、单选题
1.【答案】B
【解析】【解答】对重物受力分析,受重力和拉力,加速下降,根据牛顿第二定律,有:m′g﹣T=m′a①再对人受力分析,受到重力、拉力和支持力,根据共点力平衡条件,有:N+T=mg ②
由①②,解得
N=(m﹣m′)g+m′a
故选B.
【分析】先对重物受力分析,受重力和拉力,加速下降,然后根据牛顿第二定律列式求出绳子的拉力;再对人受力分析,受到重力、拉力和支持力,根据平衡条件求出支持力,而台秤读数等于支持力.
2.【答案】B
【解析】【解答】解:设杆转动α角,“┏”型均匀杆的总质量为m,力F的力矩等于BC段重力的力矩,根据力矩平衡条件,有: ( mg)?x=F?Lcosα;(x为BC段的中点与O点连线的水平分量)
由于x先变大后变小,故( mg)?x先变大后变小,F?Lcosα先变大后变小,故ACD错误,B正确;
故选:B.
【分析】BO段与AO段的重力的力矩恰好平衡,故拉力的力矩等于BC段重力的力矩,然后根据力矩平衡条件列式分析.
3.【答案】B
【解析】【解答】A、由题意可知,三个小球均处于静止状态,故各物体所受合力都为零,故合力相等,故A错误;B、对A受力分析可知,A受重力和BC的支持力而处于平衡,故BC对A的作用力的合力方向竖直同上,故B正确;
C、对B受力分析,B受重力、支持力、A的弹力及地面的摩擦力,若这些力能使物体平衡,则BC间没有弹力,故C错误;
D、若圆柱体光滑,则下面的两物体BC将不能保持静止,故D错误;
故选:B.
【分析】对物体进行受力分析,由共点力的平衡条件可知它们受到的合力均为零;用假设法可得出圆柱体光滑时能否平衡.
4.【答案】A
【解析】解答:A、由图可知,OA之间的距离为a , OB之间的距离为b , OC之间的距离为c , 设OB杆的质量为m0 , 秤砣与A之间的距离为x , 当秤砣在A点到达平衡时:m0g?c=(m+m′)g?a ①
当秤砣在距离A点的距离为x到达平衡时.得:
m0g?c+Mg?b=m′ga+mg(a+x)
联立以上二式得:M?b=m?x ②
即,重物的质量与秤砣到A点的距离成正比,所以杆秤上的刻度一定是均匀的.故A正确;
B、由②式可知, ,其它条件不变,OB之间的距离b越小,称量的质量的范围越大.故B错误;
C、由②式可知, ,其它条件不变,砣的质量越大,秤量范围越大.故C错误;
D、若在加速上升的电梯中,设加速度大小为:a0 , 当秤砣在距离A点的距离为x到达平衡时.得:
m0(g+a0)?c+M(g+a0)?b=m′(g+a0)?a+m(g+a0)(a+x)
整理得:M?b=m?x , 可知与电梯的加速度无关.所以如果在加速上升的电梯中,杆秤称量计数不变.
故D错误.
故选:A
分析:杆秤利用杠杆的平衡条件,通过力臂的大小关系得出物体的质量与秤砣的质量之间的关系,测量物体的质量.该题根据该原理解答即可.
5.【答案】C
【解析】【解答】解:设杠杆每一格长度是L, 当B处的作用力与杠杆垂直时,力臂最大,此时作用力最小,
由杠杆平衡条件可得:FALA=FB最小LB , 即:2N×2L=FB最小×4L,
则FB最小=1N,当作用在B处的力与杠杆不垂直时,力臂小于4L,
作用力大于1N,因此要使杠杆平衡,作用在B处的力F≥1N,故ABD错误,C正确;
故选C.
【分析】根据杠杆平衡的条件和杠杆中最小力的问题进行分析,即动力乘以动力臂等于阻力乘以阻力臂,支点与力的作用点的连线为最长力臂.
6.【答案】D
【解析】【解答】解:对木棒分析可知,以左侧为支点,木棒受重力和F的作用下处于力矩平衡状态,故力F的力矩与重力力矩平衡;则有:mgL=FL′ 在移动过程中,重力不变,重力力臂减小,故重力的力矩减小,根据力矩平衡可知,力F的力矩减小;
由图可知,重力力臂和F的力臂之比恒定,故F保持不变;
故D正确,ABC错误.
故选:D.
【分析】木棒在重力和拉力作用下处于平衡状态,分别明确二者的力臂,再根据力矩平衡条件即可分析力矩与力的变化情况.
7.【答案】C
【解析】【解答】A、由于B点始终处于平衡状态,故B点受到的力的大小为各力的合力.故B点在变化过程中受到的力始终为0.故大小不变.故A错误B、由对A项的分析知B点受到的力始终为0,不变.故B错误.
C、由对A项的分析知B点受到的力始终为0,不变.故C正确.
D、由对A项的分析知B点受到的力始终为0,不变.故D错误.
故选:C
【分析】以B为研究对象,并受力分析.由题目中“缓慢”二字知整个变化过程中B处于平衡态.
8.【答案】C
【解析】【解答】A、不管什么情况下,使用任何机械都不会省功;实际情况下,考虑机械的摩擦,使用机械总是费功的,故A正确,B正确;
C、D、根据公式W=FS , 省力的费距离,费力的省距离,故C错误,D正确;
本题选择错误的,故选:C.
【分析】解决此题的关键是知道使用任何机械都不会省功,省力的费距离,费力的省距离.
9.【答案】A
【解析】【解答】解:先将力的作用点与支点连接起来,如图所示:
假设只有拉力F1作用,杆会顺时针转动;
假设只有拉力F2作用,杆同样会顺时针转动;
故F1和F2都产生顺时针效果的力矩;
故选:A.
【分析】先将c端与a端用直线连接起来,然后考虑拉力F1与F2的力矩是顺时针效果还是逆时针效果.
10.【答案】A
【解析】解答:将小球m2的重力按效果根据平行四边形定则进行分解如图,
由几何知识得:T=m2g ①
对m1受力分析,由平衡条件,在沿杆的方向有:m1gsin30°=Tsin30°
得:T=m1g ②
可见m1:m2的=1:1;
故选:A.
分析:将小球m2的重力按效果根据平行四边形定则进行分解,由几何知识求出m2g与绳子拉力T的关系,对m1受力分析,由平衡条件求出m1g与T的关系,进而得到m1:m2的比值.
二、填空题
11.【答案】;aRccos
【解析】【解答】由于物体m受力平衡,故细线的拉力等于mg;
当若θ为37°时杆恰好达到平衡,以B为支点,设杆长为L , 根据力矩平衡条件得:
sin37°+MgLsin37°=MgLcos37°
解得:m:M=2:3
设AB长为L , 这BC为0.8L;
若将杆换为长度不变的轻杆,杆AB受到铰链的作用力和轻绳对AB的压力,要使杆能够平衡,轻绳对AB的压力方向应在AC与AB之间,而轻绳对AB的压力等于轻绳AC和AG拉力的合力,这两个拉力大小相等,故AB在细线的两侧拉力的角平分线上,如图所示:
故 , 则α=aRccos
故答案为: ,aRccos.
【分析】对粗细均匀的均质杆AB分析受力情况,若θ为37°时恰好达到平衡,以B为支点,根据力矩平衡条件求解质量之比;若将杆换为长度不变的轻杆,轻绳对AB的压力方向沿着杆的方向,即可得到θ的大小.
12.【答案】2.73G;3.73G
【解析】【解答】以A为支点,AB受到BC的支持力和两个绳子的拉力,它们的力臂如图1,设AB杆的长度为L , 则:
竖直向下的拉力的力臂;L1=L
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL1+GL2=FBC?L3
代入数据得:FBC=3.73G
同理,以C为支点,BC受到AB的拉力和两个绳子的拉力,它们的力臂如图2,则:
竖直向下的拉力的力臂: ;
BD的拉力的力臂:
BC杆的作用力的力臂:
由力矩平衡得:GL4+GL5=FAB?L6
代入数据得:FAB=2.73G
故答案为:2.73G;3.73G
【分析】画出各个力,分别作出各个力的力臂,然后又力矩的平衡即可解答.
13.【答案】Fcosθ;先变大后变小
【解析】【解答】一竖直向上、大小为F的力作用在B点,使AB边保持水平,根据力矩平衡条件,有:
F?AB=G?d ①
(其中d为重力的力臂)
当力臂最大时,作用力最小,即F作用在C点,且与AC垂直,此时力臂最大,作用力最小,有:
F′?AC=G?d ②
联立①②两式,解得:
F′=Fcosθ
若从AB水平状态开始,用一始终沿BC方向、作用于B点的力,使板绕轴A逆时针缓慢转动90°,由于重力的力臂先增加后减小,拉力的力臂一直减小,根据力矩平衡条件,拉力先变大后变小;
故答案为:Fcosθ , 先变大后变小.
【分析】当作用力的力臂最大时,作用力最小;沿垂直AC方向、作用于C点的力最小;根据力矩平衡条件列式判断拉力的变化情况.
14.【答案】;
【解析】【解答】设OA长为l , 当绳无拉力,则弹簧的拉力的力矩与重力的力矩平衡,即:Flocsin60°=mg;
当m右移 的距离时,由力矩平衡得:Flocsin60°+Tlsin30°=mg;
解得:F= ,T=
答案为: ,
【分析】杠杆平衡的条件:动力乘以动力臂等于阻力乘以阻力臂;如图所示,根据直角三角形角与边的关系,求出绳子对杠杆拉力的力臂;再利用已知的重力和重力的力臂以及杠杆平衡的条件求出拉力F的大小.
三、解答题
15.【答案】解:作出两匀质棒AB和BC的重力及力臂如图所示,设棒长为L 将两棒的重力进行分解如图所示
对AB棒有使棒转动的合力F1=mgsin45°+mgsin45°=
切向加速度a1=
角加速度
对BC棒有使棒转动的合力F2=mgsin45°=
切向加速度a2=
角加速度
则刚释放时两棒的初角加速度之比为
答:刚释放时两棒的初角加速度之比为 .
【解析】【分析】先明确两棒的转动过程,作出受到的重力并分解,再计算出切向加速度,再计算出角加速度.
四、综合题
16.【答案】(1)
(2)
【解析】【解答】(1)过拉力作用点作竖直向下的拉力F2(2)过支点O作F1作用线的垂线段(即动力臂L1).
如图所示
【分析】(1)拉力F2的作用点为鱼线与杆的交点,阻力的方向沿绳子向下,过拉力F2的作用点表示出拉力的方向;(2)已知支点和动力的方向,根据力臂的定义过支点作力的作用线的垂线.
17.【答案】(1)对B球受力,如图:
根据力的平衡条件,有:
水平方向:Tsinθ=F
竖直方向:Tcosθ=mg
故:
F=mgtanθ
解得:
F=10 N
(2)由于绳对铁块的拉力垂直于铁块,且铁块处于静止状态,因此铁块受到的摩擦力等于铁块的重力沿斜面向下的分力,即:
【解析】【解答】(1)对B球受力,如图:
根据力的平衡条件,有:
水平方向:Tsinθ=F
竖直方向:Tcosθ=mg
故:
F=mgtanθ
解得:
F=10 N(2)由于绳对铁块的拉力垂直于铁块,且铁块处于静止状态,因此铁块受到的摩擦力等于铁块的重力沿斜面向下的分力,即:
【分析】(1)对B球受力分析,受重力、拉力F和细线的拉力T , 根据平衡条件列式求解即可;(2)铁块受重力、细线的拉力和静摩擦力,根据平衡条件列式求解.
