华师大版七年级下册:三角形的三边关系
文档属性
| 名称 | 华师大版七年级下册:三角形的三边关系 |

|
|
| 格式 | zip | ||
| 文件大小 | 252.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 20:42:56 | ||
图片预览



文档简介
(共16张PPT)
三角形的三边关系
如图,小明从家步行到学校有两条路,一条是柏油路另一条是小路.如果你是小明,你会选择哪条路去学校 为什么
家
学校
C
A
B
是否任意三条线段都组成一个三角形?
想一想
这个三角形是由三条线段组成的
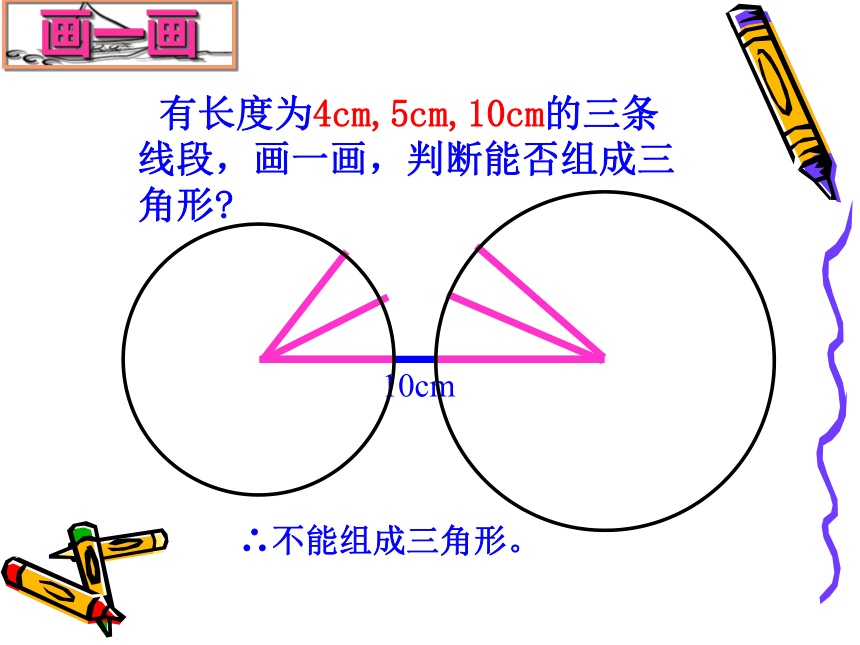
10cm
有长度为4cm,5cm,10cm的三条线段,画一画,判断能否组成三角形
画一画
∴不能组成三角形。
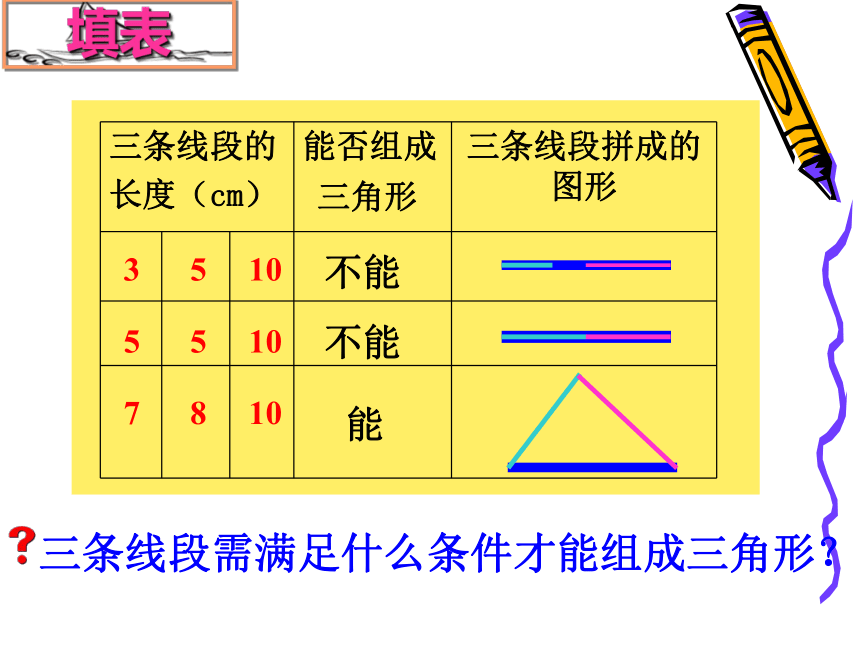
填表
三条线段的
长度(cm) 能否组成
三角形 三条线段拼成的图形
3 5 10
5 5 10
7 8 10
不能
不能
能
三条线段需满足什么条件才能组成三角形?
三条线段需满足什么条件才能组成三角形?
两条较短线段的和
要大于
最长的线段.
例1 下列长度的各组线段能否组成一个三角形
(1)15cm、9cm、7cm;(2)3cm、6cm、10cm
(3)3cm、8cm、5cm;(4)2cm、5cm、6cm
解: (1) ∵ 9+7>15, ∴能组成三角形;
(2) ∵ 3+6<10, ∴不能组成三角形;
(3) ∵ 3+5=8, ∴不能组成三角形;
(4) ∵ 2+5>6, ∴能组成三角形.
c
a
b
∴a+b>c
b+c>a
c+a>b
三角形的任意两边和大于第三边.
三角形的任意两边差小于第三边.
三角形的三边关系
两边差<第三边<两边和
例2 等腰三角形的周长为18厘米,其中一边长为4厘米,求其它两边的长
解: 第一种情况,4厘米长的边为底.
第二种情况,4厘米长的边为腰.
∴三角形的其他两边长都是7厘米.
设腰长为 x 厘米.则2x+4=18, x=7
且4+7>7, 能组成三角形.
设底边长为x厘米.则x+2x4=18, x=10
但4+4<10,不能组成三角形.
要分类讨论
例3 在△ABC中,已知a=8cm,b=5cm,则c的取值范围是 ,
3cm改:a=4cm,b=6cm.
a=2cm,b=7cm.
2cm5cm两边差<第三边<两边和
练习:课本61页1、2。
若c取奇数,则c取何值_______
三角形的稳定性
三角形的三条边固定,那么三角形的形状大小就完全固定.
以下是生活中利用三角形稳定性建造的一些图片
今天你的收获
三角形的三边关系
判断三条线段能否组成三角形
分类讨论等腰三角形的相关问题
三角形的边的取值范围
三角形的稳定性
作业
P61、 练习第3题 习题9.1—— 1
三角形的三边关系
如图,小明从家步行到学校有两条路,一条是柏油路另一条是小路.如果你是小明,你会选择哪条路去学校 为什么
家
学校
C
A
B
是否任意三条线段都组成一个三角形?
想一想
这个三角形是由三条线段组成的
10cm
有长度为4cm,5cm,10cm的三条线段,画一画,判断能否组成三角形
画一画
∴不能组成三角形。
填表
三条线段的
长度(cm) 能否组成
三角形 三条线段拼成的图形
3 5 10
5 5 10
7 8 10
不能
不能
能
三条线段需满足什么条件才能组成三角形?
三条线段需满足什么条件才能组成三角形?
两条较短线段的和
要大于
最长的线段.
例1 下列长度的各组线段能否组成一个三角形
(1)15cm、9cm、7cm;(2)3cm、6cm、10cm
(3)3cm、8cm、5cm;(4)2cm、5cm、6cm
解: (1) ∵ 9+7>15, ∴能组成三角形;
(2) ∵ 3+6<10, ∴不能组成三角形;
(3) ∵ 3+5=8, ∴不能组成三角形;
(4) ∵ 2+5>6, ∴能组成三角形.
c
a
b
∴a+b>c
b+c>a
c+a>b
三角形的任意两边和大于第三边.
三角形的任意两边差小于第三边.
三角形的三边关系
两边差<第三边<两边和
例2 等腰三角形的周长为18厘米,其中一边长为4厘米,求其它两边的长
解: 第一种情况,4厘米长的边为底.
第二种情况,4厘米长的边为腰.
∴三角形的其他两边长都是7厘米.
设腰长为 x 厘米.则2x+4=18, x=7
且4+7>7, 能组成三角形.
设底边长为x厘米.则x+2x4=18, x=10
但4+4<10,不能组成三角形.
要分类讨论
例3 在△ABC中,已知a=8cm,b=5cm,则c的取值范围是 ,
3cm
a=2cm,b=7cm.
2cm
练习:课本61页1、2。
若c取奇数,则c取何值_______
三角形的稳定性
三角形的三条边固定,那么三角形的形状大小就完全固定.
以下是生活中利用三角形稳定性建造的一些图片
今天你的收获
三角形的三边关系
判断三条线段能否组成三角形
分类讨论等腰三角形的相关问题
三角形的边的取值范围
三角形的稳定性
作业
P61、 练习第3题 习题9.1—— 1
