北师大版必修3 1.5.2 估计总体的数字特征 课件(29张)
文档属性
| 名称 | 北师大版必修3 1.5.2 估计总体的数字特征 课件(29张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 608.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 16:38:46 | ||
图片预览





文档简介
§1.5.2估计总体的数字特征
学习目标
1. 能根据实际问题的需要合理地选取样本,从样本数据中提取基本的数字特征(如平均数、标准差),并做出合理的解释.
2. 会用样本的基本数字特征估计总体的基本数字特征.
3. 形成对数据处理过程进行初步评价的意识.
复习回顾
2、中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
1、众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
3、平均数: 一般地,如果n个数 ,那
么, 叫做这n个数的平均数。
导
在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩(米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数,中位数与平均数 。
解:众数是1.75.
平均数是
基础演练
导
中位数是1.70;
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
上面是抽样调查的100位居民的月均用水量的数据,我们求出这一组样本数据的 众数,中位数和平均数 :
众数 =2.3(t)中位数=2.0(t)平均数=2.0(t)
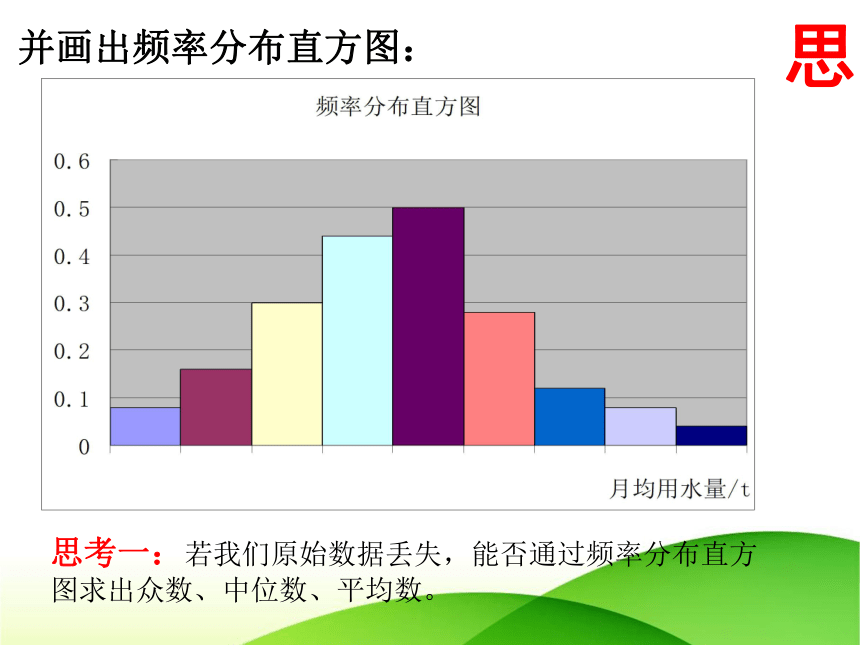
并画出频率分布直方图:
思
思考一:若我们原始数据丢失,能否通过频率分布直方图求出众数、中位数、平均数。
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
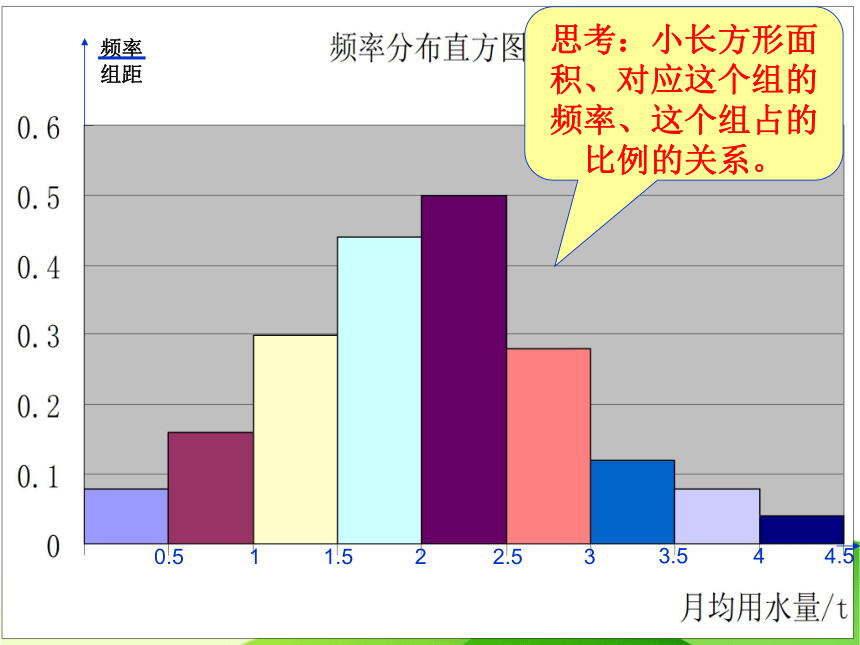
思考:小长方形面积、对应这个组的频率、这个组占的比例的关系。
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
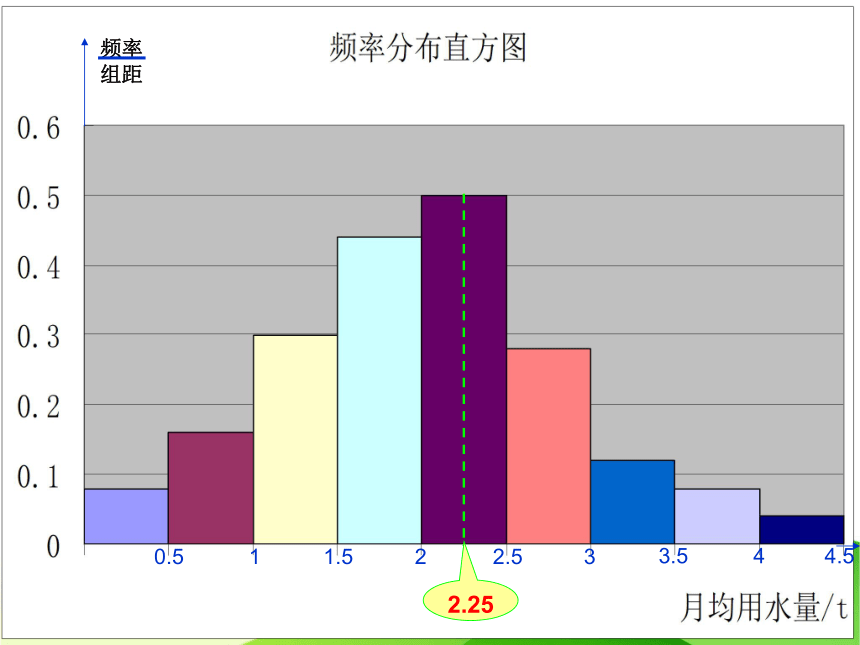
2.25
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
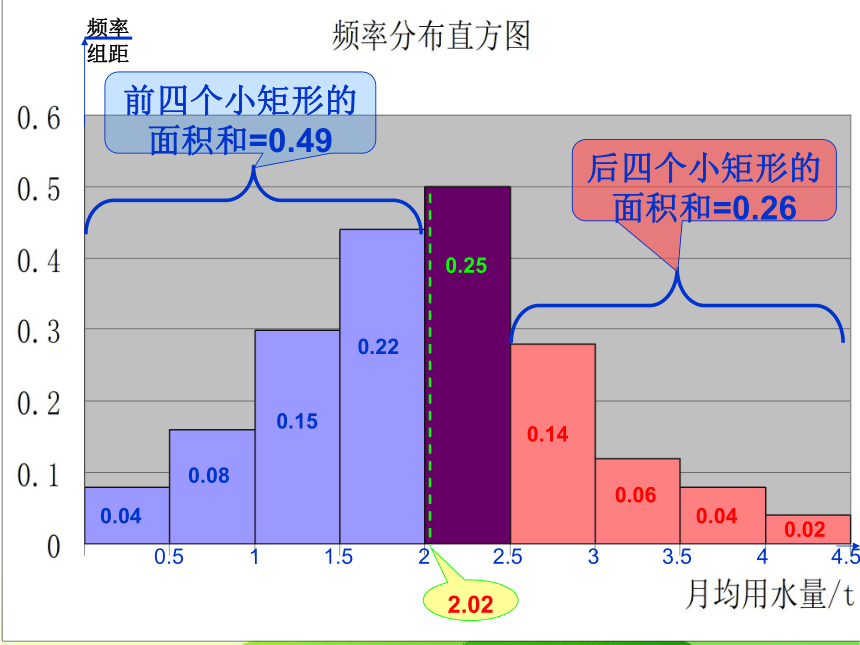
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标.
思
中位数在样本数据的频率分布直方图中,就是把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标.
思
思考二:
2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中原因吗?
答:这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,直方图已经损失一些样本信息。所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.
思
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
提示:在频率分布直方图中,各个组的平均数如何找?
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
.
.
.
.
.
.
.
.
.
0.75
1.75
2.25
2.75
3.25
3.75
4.25
1.25
0.5
提示:与小长方形面积的比例有关吗?
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
2.02
.
.
.
.
.
.
.
.
.
0.75
1.75
2.25
2.75
3.25
3.75
4.25
1.25
0.5
平均数在样本数据的频率分布直方图中,等于频率分布图中每个小长方形面积乘以小矩形底边中点的横坐标之和.
思
众数:最高矩形的中点
2.25
中位数:左右两边直方图的面积相等.
2.02
平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
2.02
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
导
1.用频率分布直方图估计众数、中位数、平均数的方法:
(1)众数:取最高小长方形底边中点的横坐标作为众数.
(2)中位数:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数.
(3)平均数:平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
知识总结
合作探究
议展
议展
探究二:为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组频数为12.
合作探究
①第二小组的频率是多少?样本容量是多少?
②若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
③在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
议展
解析:①由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,
因此,第二小组的频率为:
又因为第二小组频率=
所以样本容量=
②由图可估计该学校高一学生的达标率约为
议展
③由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内.
议展
探究三 在一次科技知识竞赛中,两组学生的成绩如下表:
分数
50
60
70
80
90
100
人
数
甲组
2
5
10
13
14
6
乙组
4
4
16
2
12
12
已经算得两个组的平均分都是80分.请根据你所学过的统计知识,进一步判断这两个组在这次竞赛中的成绩谁优谁劣,并说明理由.
解析答案
反思与感悟
议展
1.用频率分布直方图估计众数、中位数、平均数的方法:
(1)众数:取最高小长方形底边中点的横坐标作为众数.
(2)中位数:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数.
(3)平均数:平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
课堂小结
1.某同学使用计算器求30个数据的平均数时,错将其中一个
数据105输入为15,那么由此求出的平均数与实际平均数的
差是( )
(A)3.5 (B)-3 (C)3 (D)-0.5
【解析】选B.错将数据105输入为15,则平均数少
即与实际平均数的差是-3.
当堂检测
检
B
2.一位同学种了甲、乙两种树苗各1株,分别观察了9次、10次后,得到树苗高度的数据的茎叶图如图(单位:厘米),则甲、乙两种树苗高度的数据的中位数之和是( )
(A)44 (B)54 (C)50 (D)52
检
D
3. (2013·辽宁高考)某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
A.45 B.50 C.55 D.60
检
B
学习目标
1. 能根据实际问题的需要合理地选取样本,从样本数据中提取基本的数字特征(如平均数、标准差),并做出合理的解释.
2. 会用样本的基本数字特征估计总体的基本数字特征.
3. 形成对数据处理过程进行初步评价的意识.
复习回顾
2、中位数:将一组数据按大小依次排列,把处在最中间位置的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
1、众数:在一组数据中,出现次数最多的数据叫做这组数据的众数.
众数、中位数、平均数都是描述一组数据的集中趋势的特征数,只是描述的角度不同,其中以平均数的应用最为广泛.
3、平均数: 一般地,如果n个数 ,那
么, 叫做这n个数的平均数。
导
在一次中学生田径运动会上,参加男子跳高的17名运动员的成绩如下表所示:
成绩(米)
1.50
1.60
1.65
1.70
1.75
1.80
1.85
1.90
人数
2
3
2
3
4
1
1
1
分别求这些运动员成绩的众数,中位数与平均数 。
解:众数是1.75.
平均数是
基础演练
导
中位数是1.70;
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
上面是抽样调查的100位居民的月均用水量的数据,我们求出这一组样本数据的 众数,中位数和平均数 :
众数 =2.3(t)中位数=2.0(t)平均数=2.0(t)
并画出频率分布直方图:
思
思考一:若我们原始数据丢失,能否通过频率分布直方图求出众数、中位数、平均数。
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
思考:小长方形面积、对应这个组的频率、这个组占的比例的关系。
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
2.25
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
前四个小矩形的面积和=0.49
后四个小矩形的面积和=0.26
2.02
众数在样本数据的频率分布直方图中,就是最高矩形的中点的横坐标.
思
中位数在样本数据的频率分布直方图中,就是把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标.
思
思考二:
2.02这个中位数的估计值,与样本的中位数值2.0不一样,你能解释其中原因吗?
答:这是因为样本数据的频率分布直方图,只是直观地表明分布的形状,但是从直方图本身得不出原始的数据内容,直方图已经损失一些样本信息。所以由频率分布直方图得到的中位数估计值往往与样本的实际中位数值不一致.
思
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
提示:在频率分布直方图中,各个组的平均数如何找?
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
.
.
.
.
.
.
.
.
.
0.75
1.75
2.25
2.75
3.25
3.75
4.25
1.25
0.5
提示:与小长方形面积的比例有关吗?
0.5
2.5
2
1.5
1
4
3.5
3
4.5
频率
组距
0.04
0.08
0.15
0.22
0.25
0.14
0.06
0.04
0.02
2.02
.
.
.
.
.
.
.
.
.
0.75
1.75
2.25
2.75
3.25
3.75
4.25
1.25
0.5
平均数在样本数据的频率分布直方图中,等于频率分布图中每个小长方形面积乘以小矩形底边中点的横坐标之和.
思
众数:最高矩形的中点
2.25
中位数:左右两边直方图的面积相等.
2.02
平均数:频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
2.02
0.16
0.5 1 1.5 2 2.5 3 3.5 4 4.5
月均用水量/t
频率
组距
0.08
O
0.3
0.44
0.5
0.28
导
1.用频率分布直方图估计众数、中位数、平均数的方法:
(1)众数:取最高小长方形底边中点的横坐标作为众数.
(2)中位数:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数.
(3)平均数:平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
知识总结
合作探究
议展
议展
探究二:为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2∶4∶17∶15∶9∶3,第二小组频数为12.
合作探究
①第二小组的频率是多少?样本容量是多少?
②若次数在110以上(含110次)为达标,试估计该学校全体高一学生的达标率是多少?
③在这次测试中,学生跳绳次数的中位数落在哪个小组内?请说明理由.
议展
解析:①由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,
因此,第二小组的频率为:
又因为第二小组频率=
所以样本容量=
②由图可估计该学校高一学生的达标率约为
议展
③由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内.
议展
探究三 在一次科技知识竞赛中,两组学生的成绩如下表:
分数
50
60
70
80
90
100
人
数
甲组
2
5
10
13
14
6
乙组
4
4
16
2
12
12
已经算得两个组的平均分都是80分.请根据你所学过的统计知识,进一步判断这两个组在这次竞赛中的成绩谁优谁劣,并说明理由.
解析答案
反思与感悟
议展
1.用频率分布直方图估计众数、中位数、平均数的方法:
(1)众数:取最高小长方形底边中点的横坐标作为众数.
(2)中位数:在频率分布直方图中,把频率分布直方图划分左右两个面积相等的分界线与x轴交点的横坐标称为中位数.
(3)平均数:平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和.
课堂小结
1.某同学使用计算器求30个数据的平均数时,错将其中一个
数据105输入为15,那么由此求出的平均数与实际平均数的
差是( )
(A)3.5 (B)-3 (C)3 (D)-0.5
【解析】选B.错将数据105输入为15,则平均数少
即与实际平均数的差是-3.
当堂检测
检
B
2.一位同学种了甲、乙两种树苗各1株,分别观察了9次、10次后,得到树苗高度的数据的茎叶图如图(单位:厘米),则甲、乙两种树苗高度的数据的中位数之和是( )
(A)44 (B)54 (C)50 (D)52
检
D
3. (2013·辽宁高考)某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
A.45 B.50 C.55 D.60
检
B
