北师大版必修3 1.5.2 估计总体的数字特征 课件(12张)
文档属性
| 名称 | 北师大版必修3 1.5.2 估计总体的数字特征 课件(12张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1012.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 16:38:46 | ||
图片预览




文档简介
1.5.2 用样本估计总体的数字特征
数字特征有哪些呢?
平均数
中位数
众数
极差
方差
标准差
例1 在伦敦奥运会射击选拔赛中,有两位射击运动员在 一次射击测试中各射靶10次,每次命中的环数如下:
甲: 10 8 9 9 8 8 9 10 9 10
乙: 10 10 10 9 9 9 9 9 6 9
如果你是教练,你会如何评价这两位射击运动员?
如何得到这两组数据的数字特征?
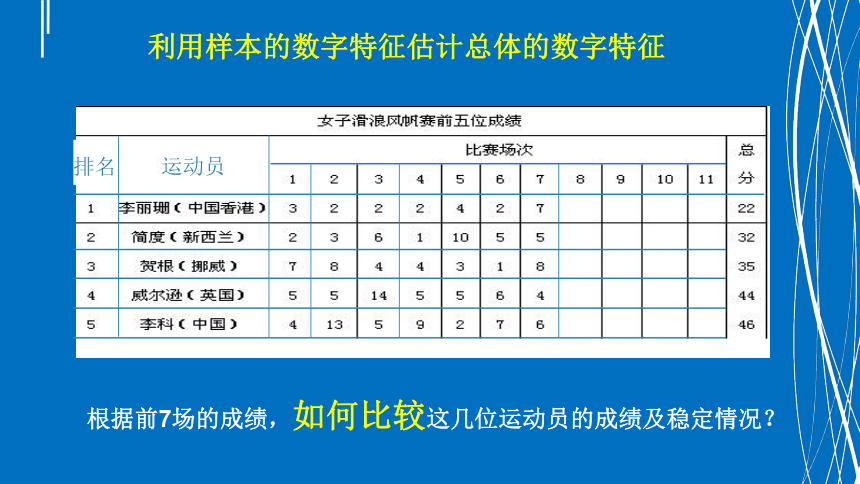
例2 在1996年美国亚特兰大奥运会上,中国香港风帆选手李丽珊,以惊人的耐力和斗志,勇夺奥运金牌,为香港体育史揭开了“突破零”的新页.在风帆比赛中,成绩以低分为优胜.比赛共11场,并以最佳的9场成绩计算最终的名次.前7场比赛结束后,排名前5位的选手积分如表所示:
排名
运动员
根据前7场的成绩,如何比较这几位运动员的成绩及稳定情况?
利用样本的数字特征估计总体的数字特征
同样的样本,得到的频率分布直方图一样吗?
同样的抽样方法得到的样本一样吗?
不同的人抽取的样本一样吗?
根据频率分布直方图如何得到样本的数字特征,从而估计总体的数字特征?
绘制频率分布直方图的步骤?
如何根据样本的频率分布直方图估计总体的数字特征?
例3 某校高三年级有200人参加了数学竞赛,学校从中抽取了50人的成绩,频率分布直方图如下:
请根据直方图估计此次数学竞赛成绩的平均数、中位数、众数。
例4
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.
通过抽样调查,获得100位居民2007年的月均用水量如下表(单位:t):
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
2.画出该样本的频率分布直方图,并以此估计该市居民用水量的分布。
3.根据频率分布直方图估计该市居民用水量的平均数、中位数、众数。
1.请直接计算该样本的平均数、中位树、众数。
小组协作:
4.比较1、3两种方式得到的数字特征,有什么发现?有什么想法?
通过这节课,你收获了什么?
数字特征有哪些呢?
平均数
中位数
众数
极差
方差
标准差
例1 在伦敦奥运会射击选拔赛中,有两位射击运动员在 一次射击测试中各射靶10次,每次命中的环数如下:
甲: 10 8 9 9 8 8 9 10 9 10
乙: 10 10 10 9 9 9 9 9 6 9
如果你是教练,你会如何评价这两位射击运动员?
如何得到这两组数据的数字特征?
例2 在1996年美国亚特兰大奥运会上,中国香港风帆选手李丽珊,以惊人的耐力和斗志,勇夺奥运金牌,为香港体育史揭开了“突破零”的新页.在风帆比赛中,成绩以低分为优胜.比赛共11场,并以最佳的9场成绩计算最终的名次.前7场比赛结束后,排名前5位的选手积分如表所示:
排名
运动员
根据前7场的成绩,如何比较这几位运动员的成绩及稳定情况?
利用样本的数字特征估计总体的数字特征
同样的样本,得到的频率分布直方图一样吗?
同样的抽样方法得到的样本一样吗?
不同的人抽取的样本一样吗?
根据频率分布直方图如何得到样本的数字特征,从而估计总体的数字特征?
绘制频率分布直方图的步骤?
如何根据样本的频率分布直方图估计总体的数字特征?
例3 某校高三年级有200人参加了数学竞赛,学校从中抽取了50人的成绩,频率分布直方图如下:
请根据直方图估计此次数学竞赛成绩的平均数、中位数、众数。
例4
我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a,用水量不超过a的部分按平价收费,超出a的部分按议价收费.
通过抽样调查,获得100位居民2007年的月均用水量如下表(单位:t):
3.1 2.5 2.0 2.0 1.5 1.0 1.6 1.8 1.9 1.6
3.4 2.6 2.2 2.2 1.5 1.2 0.2 0.4 0.3 0.4
3.2 2.7 2.3 2.1 1.6 1.2 3.7 1.5 0.5 3.8
3.3 2.8 2.3 2.2 1.7 1.3 3.6 1.7 0.6 4.1
3.2 2.9 2.4 2.3 1.8 1.4 3.5 1.9 0.8 4.3
3.0 2.9 2.4 2.4 1.9 1.3 1.4 1.8 0.7 2.0
2.5 2.8 2.3 2.3 1.8 1.3 1.3 1.6 0.9 2.3
2.6 2.7 2.4 2.1 1.7 1.4 1.2 1.5 0.5 2.4
2.5 2.6 2.3 2.1 1.6 1.0 1.0 1.7 0.8 2.4
2.8 2.5 2.2 2.0 1.5 1.0 1.2 1.8 0.6 2.2
2.画出该样本的频率分布直方图,并以此估计该市居民用水量的分布。
3.根据频率分布直方图估计该市居民用水量的平均数、中位数、众数。
1.请直接计算该样本的平均数、中位树、众数。
小组协作:
4.比较1、3两种方式得到的数字特征,有什么发现?有什么想法?
通过这节课,你收获了什么?
