2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版九年级上册数学《第1章 反比例函数》单元测试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 392.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 17:01:49 | ||
图片预览




文档简介
2021-2022学年鲁教五四新版九年级上册数学《第1章
反比例函数》单元测试卷
一.选择题
1.下列函数中y是x的反比例函数的是( )
A.
B.xy=8
C.
D.
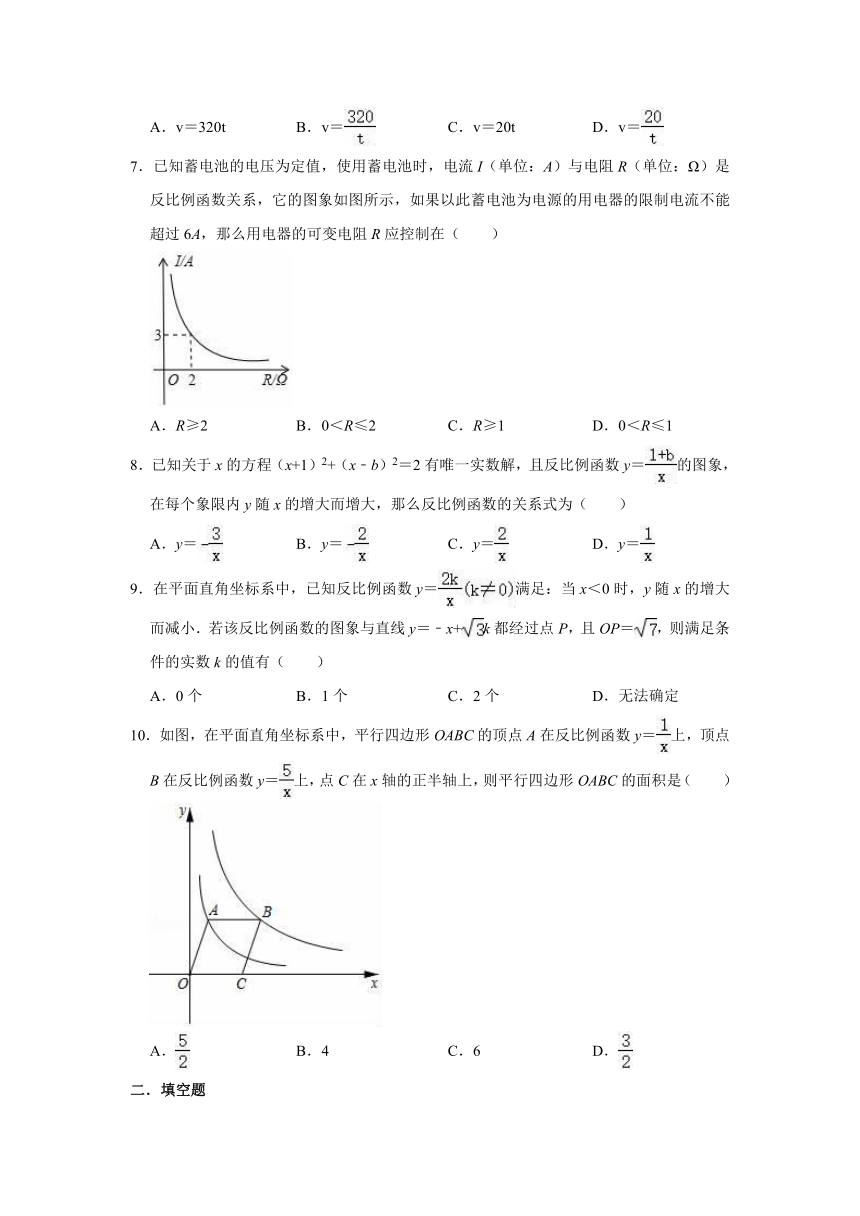
2.如图,以原点为圆心的圆与反比例函数的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
A.﹣3
B.﹣2
C.﹣1
D.﹣4
3.对于双曲线,x>0时,y随x的增大而增大,则k的取值范围为( )
A.k<2
B.k≤2
C.k>2
D.k≥2
4.在同一直角坐标系中,一次函数y=kx+3与反比例函数y=的图象位置可能是( )
A.
B.
C.
D.
5.反比例函数y=的图象经过点A(﹣1,﹣2),则当x>1时,函数值y的取值范围是( )
A.y>1
B.0<y<1
C.y>2
D.0<y<2
6.一司机驾驶汽车从甲地去乙地,他以平均80千米/小时的速度用了4个小时到达乙地,当他按原路匀速返回时.汽车的速度v千米/小时与时间t小时的函数关系是( )
A.v=320t
B.v=
C.v=20t
D.v=
7.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器的限制电流不能超过6A,那么用电器的可变电阻R应控制在( )
A.R≥2
B.0<R≤2
C.R≥1
D.0<R≤1
8.已知关于x的方程(x+1)2+(x﹣b)2=2有唯一实数解,且反比例函数y=的图象,在每个象限内y随x的增大而增大,那么反比例函数的关系式为( )
A.y=
B.y=
C.y=
D.y=
9.在平面直角坐标系中,已知反比例函数y=满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线y=﹣x+k都经过点P,且OP=,则满足条件的实数k的值有( )
A.0个
B.1个
C.2个
D.无法确定
10.如图,在平面直角坐标系中,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A.
B.4
C.6
D.
二.填空题
11.已知函数是反比例函数,则n的值为
.
12.把一个长、宽、高分别为3cm,2cm,1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积s(cm2)与高h(cm)之间的函数关系式为
.
13.在双曲线y=的每一支上,y都随着x的增大而减小,则k的取值范围为
.
14.如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=的图象与正方形的一个交点,则图中阴影部分的面积是
.
15.反比例函数图象经过点(2,﹣3),则它的解析式为
.
16.已知点A(2,m+1)在反比例函数y=的图象上,则m=
.
17.函数y=,当y≥﹣2时,x的取值范围是
(可结合图象求解).
18.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=
.
19.如图,直线y=x﹣1与x轴交于点B,与双曲线y=(x>0)交于点A,过点B作x轴的垂线,与双曲线y=交于点C.且AB=AC,则k的值为
.
20.在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度ρ也随之改变.ρ与V在一定范围内满足,它的图象如图所示,则该气体的质量m为
kg.
三.解答题
21.已知反比例函数y=的图象分别位于第二、第四象限,化简:﹣+.
22.小明在研究矩形面积S与矩形的边长x,y之间的关系时,得到下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
4
3
2
1
0.5
结果发现一个数据被墨水涂黑了
(1)被墨水涂黑的数据为
.
(2)y与x之间的函数关系式为
,且y随x的增大而
.
(3)如图是小明画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1和S2的大小关系,并说明理由.
(4)在(3)的条件下,DE交BC于点G,反比例函数y=的图象经过点G交AB于点H,连接OG、OH,则四边形OGBH的面积为
.
23.如图,在平面直角坐标系xOy中,A(﹣1,2).
(1)将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是
.
(2)点C与点A关于原点O对称,则点C的坐标是
.
(3)反比例函数的图象经过点B,则它的解析式是
.
(4)一次函数的图象经过A,C两点,则它的解析式是
.
24.函数揭示了两个变量之间的关系,它的表示方法有三种:表格法、图象法、解析式法.请你根据学习函数的经验,完成对函数y=+m的探究.下表是函数y与自变量x的几组对应值:
x
…
﹣3
﹣2
﹣1
0
2
3
4
5
…
y
…
﹣0.5
﹣1
﹣2
﹣5
7
4
3
2.5
…
(1)函数y=+m自变量x的取值范围为
.
(2)根据表格中的数据,得k=
,m=
.并在右面平面直角坐标系xOy中,画出该函数的图象.
(3)请根据画出的函数图象,直接写出该函数的一条性质:
.
(4)利用所学函数知识,仔细观察上面表格和函数图象,直接写出不等式>﹣m+2x﹣5的解集.
25.如图所示,一次函数y=kx+b与反比例函数y=的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式.
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
26.下列函数中,哪些表示y是x的反比例函数:(1)y=;(2)y=;(3)xy=6;(4)3x+y=0;(5)x﹣2y=1;(6)3xy+2=0.
27.如图,在平面直角坐标系中,四边形ABCD是菱形,点A(0,4),B(﹣3,0)反比例函数y=(k为常数,k≠0,x>0)的图象经过点D.
(1)填空:k=
.
(2)已知在y=的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
参考答案与试题解析
一.选择题
1.解:A、y是x2的反比例函数,不符合题意;
B、由xy=8,可得y=,故y与x成反比例函数,符合题意;
C、y是x+5的反比例函数,不符合题意;
D、此函数式不是反比例函数,不符合题意;
故选:B.
2.解:把x=1代入y=,得y=3,故A点坐标为(1,3);
∵A、B关于y=x对称,则B点坐标为(3,1);
又∵B和C关于原点对称,
∴C点坐标为(﹣3,﹣1),
∴点C的横坐标为﹣3.
故选:A.
3.解:∵双曲线,x>0时,y随x的增大而增大,
∴k﹣2<0
∴k<2,
故选:A.
4.解:当k>0时,有y=kx+3过一、二、三象限,反比例函数y=的过一、三象限,A正确;
由函数y=kx+3过点(0,3),可排除B、C;
当k<0时,y=kx+3过一、二、四象限,反比例函数y=的过﹣、三象限,排除D.
故选:A.
5.解:∵反比例函数y=的图象经过点A(﹣1,﹣2),
∴﹣2=,
∴k=2,
∴y=,
当x=1,y=2,
当x>1时,函数值的范围为0<y<2.
故选:D.
6.解:由题意vt=80×4,
则v=.
故选:B.
7.解:设反比例函数关系式为:I=,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I=,
当I≤6时,则≤6,
R≥1,
故选:C.
8.解:关于x的方程(x+1)2+(x﹣b)2=2化成一般形式是:2x2+(2﹣2b)x+(b2﹣1)=0,
△=(2﹣2b)2﹣8(b2﹣1)=﹣4(b+3)(b﹣1)=0,
解得:b=﹣3或1.
∵反比例函数y=的图象,在每个象限内y随x的增大而增大,
∴1+b<0
∴b<﹣1,
∴b=﹣3.
则反比例函数的解析式是:y=﹣.
故选:B.
9.解:∵反比例函数y=(k≠0),当x<0时,y随x的增大而减小,
∴k>0,
设P(x,y),则xy=2k,y+x=k,
∵x、y为实数,x、y可看作一元二次方程m2﹣km+2k=0的两根,
∴△=3k2﹣8k≥0,解得k≥或k≤0(舍去),
又∵OP2=x2+y2,
∴x2+y2=7,即(x+y)2﹣2xy=7,
(k)2﹣4k=7,
解得k=﹣1或,而k≥,
故不存在满足条件的k.
故选:A.
10.解:如图作BD⊥x轴于D,延长BA交y轴于E,
∵四边形OABC是平行四边形,
∴AB∥OC,OA=BC,
∴BE⊥y轴,
∴OE=BD,
∴Rt△AOE≌Rt△CBD(HL),
根据系数k的几何意义,S矩形BDOE=5,S△AOE=,
∴四边形OABC的面积=5﹣﹣=4,
故选:B.
二.填空题
11.解:∵函数是反比例函数,
∴n+1≠0且n2﹣2=﹣1,
∴n=1,
故答案为:1.
12.解:由题意可得:sh=3×2×1,
则s=.
故答案为:s=.
13.解:由题意得:2﹣k>0,
解得:k<2,
故答案为:k<2.
14.解:把P(2a,a)代入y=得2a?a=2,解得a=1或﹣1,
∵点P在第一象限,
∴a=1,
∴P点坐标为(2,1),
∴正方形的面积=4×4=16,
∴图中阴影部分的面积=S正方形=4.
故答案为4.
15.解:设反比例函数的解析式为y=(k≠0),
因为函数经过点P(2,﹣3),
∴得k=2×(﹣3)=﹣6,
∴反比例函数解析式为y=﹣.
故答案为:y=﹣.
16.解:∵点A(2,m+1)在反比例函数y=的图象上,
∴m+1=﹣,
解得m=﹣7.
故答案为:﹣7.
17.解:当y≥﹣2时,反比例函数图象位于直线y=﹣2的上方,它的图象在一、三象限,
所以对应的x的取值范围是x≤﹣2或x>0.
18.解:∵反比例函数y1=(x>0)及y2=(x>0)的图象均在第一象限内,
∴k1>0,k2>0.
∵AP⊥x轴,
∴S△OAP=k1,S△OBP=k2.
∴S△OAB=S△OAP﹣S△OBP=(k1﹣k2)=3,
解得:k1﹣k2=6.
故答案为:6
19.解:∵直线y=x﹣1与x轴交于点B,
∴当y=0时,x=2,
∴点B的坐标为(2,0),
又∵过点B作x轴的垂线,与双曲线y=交于点C,
∴点C的坐标为(2,),
∵AB=AC,
∴点A在线段BC的垂直平分线上,
∴点A的纵坐标为,
∵点A在双曲线y=上,
∴,得x=4,
又∵点A(4,)在直线y=x﹣1上,
∴
解得k=4.
故答案为:4.
20.解:根据题意得,且过点(5,1.4),
∴m=5×1.4=7kg.
故答案为:7.
三.解答题
21.解:∵反比例函数y=的图象分别位于第二、第四象限,
∴k<0,
∴k﹣1<0,
∴﹣+=+=k+4+=k+4+|k﹣1|=k+4﹣k+1=5.
22.解:(1)从表格可以看出xy=6,
∴墨水盖住的数据是1.5;
故答案为1.5;
(2)由xy=6,得到y=,y随x的增大而减少;
故答案为y=;减少;
(3)S1=OA?OC=k=6,S2=OD?OF=k=6,
∴S1=S2;
(4)∵S四边形OCBA=OA?OB=6,S△OCG=OD?OG=×2=1,S△OAH=OA?OH=×2=1,
∴S四边形OGBH=S四边形OCBA﹣S△OCG﹣S△OAH=6﹣1﹣1=4;
故答案为4;
23.解:(1)将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是(2,3);
(2)点C与点A关于原点O对称,则点C的坐标是(1,﹣2);
(3)设反比例函数解析式为y=,
把B(2,3)代入得:k=6,
∴反比例函数解析式为y=;
(4)设一次函数解析式为y=mx+n,
把A(﹣1,2)与C(1,﹣2)代入得:,
解得:,
则一次函数解析式为y=﹣2x.
故答案为:(1)(2,3);(2)(1,﹣2);(3)y=;(4)y=﹣2x.
24.解:(1)∵x﹣1≠0,
∴x≠1,
故答案为x≠1;
(2)把(﹣1,﹣2)(0,﹣5)代入y=+m得,
解得m=1,k=6,
故答案为6,1;
画出函数图象如图所示:
(3)由图象可得,当x>1时,y随x的增大而减小(答案不唯一),
故答案为当x>1时,y随x的增大而减小(答案不唯一);
(4)由y=2x﹣5可知,当x=0时,y=﹣5,当x=4时,y=3,
∴直线y=2x﹣5经过点(0,﹣5),(4,3),
∵点(0,﹣5),(4,3)在函数y=+m的图象上,
∵直线y=2x﹣5与函数y=+m的图象的交点为(0,﹣5),(4,3),
由图象可得,不等式>﹣m+2x﹣5的解集x<0或1<x<4.
25.解:(1)将点A(2,4)代入y=,得:m=8,
则反比例函数解析式为y=,
当x=﹣4时,y=﹣2,
则点B(﹣4,﹣2),
将点A(2,4)、B(﹣4,﹣2)代入y=kx+b,
得:,
解得:,
则一次函数解析式为y=x+2;
(2)由题意知BC=2,
则△ACB的面积=×2×6=6.
26.解:(1)y=不是反比例函数.
(2)∵y=,
∴xy=.
∴y=,是反比例函数.
(3)∵xy=6,
∴y=,是反比例函数.
(4)∵3x+y=0,
∴y=﹣3x,不是反比例函数.
(5)∵x﹣2y=1,
∴2y=x﹣1.
∴y=x﹣,不是反比例函数.
(6)∵3xy+2=0,
∴xy=﹣.
∴y=,是反比例函数.
27.解:(1)∵点A(0,4),B(﹣3,0),
∴OA=4,OB=3,
∴AB=5,
∵四边形ABCD是菱形,
∴AD=5,
即点D的横坐标是5,
∴点D的坐标为(5,4),
∴4=,得k=20,
故答案为:20;
(2)∵四边形ABMN是平行四边形,∴AN∥BM,AN=BM,
∴AN可以看作是BM经过平移得到的,
首先BM向右平移了3个单位长度,
∴N点的横坐标为3,代入y=,得点N的纵坐标为y=,
∴M点的纵坐标为﹣4=,
∴M点的坐标为(0,).
反比例函数》单元测试卷
一.选择题
1.下列函数中y是x的反比例函数的是( )
A.
B.xy=8
C.
D.
2.如图,以原点为圆心的圆与反比例函数的图象交于A、B、C、D四点,已知点A的横坐标为1,则点C的横坐标( )
A.﹣3
B.﹣2
C.﹣1
D.﹣4
3.对于双曲线,x>0时,y随x的增大而增大,则k的取值范围为( )
A.k<2
B.k≤2
C.k>2
D.k≥2
4.在同一直角坐标系中,一次函数y=kx+3与反比例函数y=的图象位置可能是( )
A.
B.
C.
D.
5.反比例函数y=的图象经过点A(﹣1,﹣2),则当x>1时,函数值y的取值范围是( )
A.y>1
B.0<y<1
C.y>2
D.0<y<2
6.一司机驾驶汽车从甲地去乙地,他以平均80千米/小时的速度用了4个小时到达乙地,当他按原路匀速返回时.汽车的速度v千米/小时与时间t小时的函数关系是( )
A.v=320t
B.v=
C.v=20t
D.v=
7.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器的限制电流不能超过6A,那么用电器的可变电阻R应控制在( )
A.R≥2
B.0<R≤2
C.R≥1
D.0<R≤1
8.已知关于x的方程(x+1)2+(x﹣b)2=2有唯一实数解,且反比例函数y=的图象,在每个象限内y随x的增大而增大,那么反比例函数的关系式为( )
A.y=
B.y=
C.y=
D.y=
9.在平面直角坐标系中,已知反比例函数y=满足:当x<0时,y随x的增大而减小.若该反比例函数的图象与直线y=﹣x+k都经过点P,且OP=,则满足条件的实数k的值有( )
A.0个
B.1个
C.2个
D.无法确定
10.如图,在平面直角坐标系中,平行四边形OABC的顶点A在反比例函数y=上,顶点B在反比例函数y=上,点C在x轴的正半轴上,则平行四边形OABC的面积是( )
A.
B.4
C.6
D.
二.填空题
11.已知函数是反比例函数,则n的值为
.
12.把一个长、宽、高分别为3cm,2cm,1cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积s(cm2)与高h(cm)之间的函数关系式为
.
13.在双曲线y=的每一支上,y都随着x的增大而减小,则k的取值范围为
.
14.如图,在平面直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(2a,a)是反比例函数y=的图象与正方形的一个交点,则图中阴影部分的面积是
.
15.反比例函数图象经过点(2,﹣3),则它的解析式为
.
16.已知点A(2,m+1)在反比例函数y=的图象上,则m=
.
17.函数y=,当y≥﹣2时,x的取值范围是
(可结合图象求解).
18.如图,直线l⊥x轴于点P,且与反比例函数y1=(x>0)及y2=(x>0)的图象分别交于点A,B,连接OA,OB,已知△OAB的面积为3,则k1﹣k2=
.
19.如图,直线y=x﹣1与x轴交于点B,与双曲线y=(x>0)交于点A,过点B作x轴的垂线,与双曲线y=交于点C.且AB=AC,则k的值为
.
20.在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度ρ也随之改变.ρ与V在一定范围内满足,它的图象如图所示,则该气体的质量m为
kg.
三.解答题
21.已知反比例函数y=的图象分别位于第二、第四象限,化简:﹣+.
22.小明在研究矩形面积S与矩形的边长x,y之间的关系时,得到下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
4
3
2
1
0.5
结果发现一个数据被墨水涂黑了
(1)被墨水涂黑的数据为
.
(2)y与x之间的函数关系式为
,且y随x的增大而
.
(3)如图是小明画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形OABC的面积记为S1,矩形ODEF的面积记为S2,请判断S1和S2的大小关系,并说明理由.
(4)在(3)的条件下,DE交BC于点G,反比例函数y=的图象经过点G交AB于点H,连接OG、OH,则四边形OGBH的面积为
.
23.如图,在平面直角坐标系xOy中,A(﹣1,2).
(1)将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是
.
(2)点C与点A关于原点O对称,则点C的坐标是
.
(3)反比例函数的图象经过点B,则它的解析式是
.
(4)一次函数的图象经过A,C两点,则它的解析式是
.
24.函数揭示了两个变量之间的关系,它的表示方法有三种:表格法、图象法、解析式法.请你根据学习函数的经验,完成对函数y=+m的探究.下表是函数y与自变量x的几组对应值:
x
…
﹣3
﹣2
﹣1
0
2
3
4
5
…
y
…
﹣0.5
﹣1
﹣2
﹣5
7
4
3
2.5
…
(1)函数y=+m自变量x的取值范围为
.
(2)根据表格中的数据,得k=
,m=
.并在右面平面直角坐标系xOy中,画出该函数的图象.
(3)请根据画出的函数图象,直接写出该函数的一条性质:
.
(4)利用所学函数知识,仔细观察上面表格和函数图象,直接写出不等式>﹣m+2x﹣5的解集.
25.如图所示,一次函数y=kx+b与反比例函数y=的图象交于A(2,4),B(﹣4,n)两点.
(1)分别求出一次函数与反比例函数的表达式.
(2)过点B作BC⊥x轴,垂足为点C,连接AC,求△ACB的面积.
26.下列函数中,哪些表示y是x的反比例函数:(1)y=;(2)y=;(3)xy=6;(4)3x+y=0;(5)x﹣2y=1;(6)3xy+2=0.
27.如图,在平面直角坐标系中,四边形ABCD是菱形,点A(0,4),B(﹣3,0)反比例函数y=(k为常数,k≠0,x>0)的图象经过点D.
(1)填空:k=
.
(2)已知在y=的图象上有一点N,y轴上有一点M,且四边形ABMN是平行四边形,求点M的坐标.
参考答案与试题解析
一.选择题
1.解:A、y是x2的反比例函数,不符合题意;
B、由xy=8,可得y=,故y与x成反比例函数,符合题意;
C、y是x+5的反比例函数,不符合题意;
D、此函数式不是反比例函数,不符合题意;
故选:B.
2.解:把x=1代入y=,得y=3,故A点坐标为(1,3);
∵A、B关于y=x对称,则B点坐标为(3,1);
又∵B和C关于原点对称,
∴C点坐标为(﹣3,﹣1),
∴点C的横坐标为﹣3.
故选:A.
3.解:∵双曲线,x>0时,y随x的增大而增大,
∴k﹣2<0
∴k<2,
故选:A.
4.解:当k>0时,有y=kx+3过一、二、三象限,反比例函数y=的过一、三象限,A正确;
由函数y=kx+3过点(0,3),可排除B、C;
当k<0时,y=kx+3过一、二、四象限,反比例函数y=的过﹣、三象限,排除D.
故选:A.
5.解:∵反比例函数y=的图象经过点A(﹣1,﹣2),
∴﹣2=,
∴k=2,
∴y=,
当x=1,y=2,
当x>1时,函数值的范围为0<y<2.
故选:D.
6.解:由题意vt=80×4,
则v=.
故选:B.
7.解:设反比例函数关系式为:I=,
把(2,3)代入得:k=2×3=6,
∴反比例函数关系式为:I=,
当I≤6时,则≤6,
R≥1,
故选:C.
8.解:关于x的方程(x+1)2+(x﹣b)2=2化成一般形式是:2x2+(2﹣2b)x+(b2﹣1)=0,
△=(2﹣2b)2﹣8(b2﹣1)=﹣4(b+3)(b﹣1)=0,
解得:b=﹣3或1.
∵反比例函数y=的图象,在每个象限内y随x的增大而增大,
∴1+b<0
∴b<﹣1,
∴b=﹣3.
则反比例函数的解析式是:y=﹣.
故选:B.
9.解:∵反比例函数y=(k≠0),当x<0时,y随x的增大而减小,
∴k>0,
设P(x,y),则xy=2k,y+x=k,
∵x、y为实数,x、y可看作一元二次方程m2﹣km+2k=0的两根,
∴△=3k2﹣8k≥0,解得k≥或k≤0(舍去),
又∵OP2=x2+y2,
∴x2+y2=7,即(x+y)2﹣2xy=7,
(k)2﹣4k=7,
解得k=﹣1或,而k≥,
故不存在满足条件的k.
故选:A.
10.解:如图作BD⊥x轴于D,延长BA交y轴于E,
∵四边形OABC是平行四边形,
∴AB∥OC,OA=BC,
∴BE⊥y轴,
∴OE=BD,
∴Rt△AOE≌Rt△CBD(HL),
根据系数k的几何意义,S矩形BDOE=5,S△AOE=,
∴四边形OABC的面积=5﹣﹣=4,
故选:B.
二.填空题
11.解:∵函数是反比例函数,
∴n+1≠0且n2﹣2=﹣1,
∴n=1,
故答案为:1.
12.解:由题意可得:sh=3×2×1,
则s=.
故答案为:s=.
13.解:由题意得:2﹣k>0,
解得:k<2,
故答案为:k<2.
14.解:把P(2a,a)代入y=得2a?a=2,解得a=1或﹣1,
∵点P在第一象限,
∴a=1,
∴P点坐标为(2,1),
∴正方形的面积=4×4=16,
∴图中阴影部分的面积=S正方形=4.
故答案为4.
15.解:设反比例函数的解析式为y=(k≠0),
因为函数经过点P(2,﹣3),
∴得k=2×(﹣3)=﹣6,
∴反比例函数解析式为y=﹣.
故答案为:y=﹣.
16.解:∵点A(2,m+1)在反比例函数y=的图象上,
∴m+1=﹣,
解得m=﹣7.
故答案为:﹣7.
17.解:当y≥﹣2时,反比例函数图象位于直线y=﹣2的上方,它的图象在一、三象限,
所以对应的x的取值范围是x≤﹣2或x>0.
18.解:∵反比例函数y1=(x>0)及y2=(x>0)的图象均在第一象限内,
∴k1>0,k2>0.
∵AP⊥x轴,
∴S△OAP=k1,S△OBP=k2.
∴S△OAB=S△OAP﹣S△OBP=(k1﹣k2)=3,
解得:k1﹣k2=6.
故答案为:6
19.解:∵直线y=x﹣1与x轴交于点B,
∴当y=0时,x=2,
∴点B的坐标为(2,0),
又∵过点B作x轴的垂线,与双曲线y=交于点C,
∴点C的坐标为(2,),
∵AB=AC,
∴点A在线段BC的垂直平分线上,
∴点A的纵坐标为,
∵点A在双曲线y=上,
∴,得x=4,
又∵点A(4,)在直线y=x﹣1上,
∴
解得k=4.
故答案为:4.
20.解:根据题意得,且过点(5,1.4),
∴m=5×1.4=7kg.
故答案为:7.
三.解答题
21.解:∵反比例函数y=的图象分别位于第二、第四象限,
∴k<0,
∴k﹣1<0,
∴﹣+=+=k+4+=k+4+|k﹣1|=k+4﹣k+1=5.
22.解:(1)从表格可以看出xy=6,
∴墨水盖住的数据是1.5;
故答案为1.5;
(2)由xy=6,得到y=,y随x的增大而减少;
故答案为y=;减少;
(3)S1=OA?OC=k=6,S2=OD?OF=k=6,
∴S1=S2;
(4)∵S四边形OCBA=OA?OB=6,S△OCG=OD?OG=×2=1,S△OAH=OA?OH=×2=1,
∴S四边形OGBH=S四边形OCBA﹣S△OCG﹣S△OAH=6﹣1﹣1=4;
故答案为4;
23.解:(1)将点A向右平移3个单位长度,再向上平移1个单位长度,得到点B,则点B的坐标是(2,3);
(2)点C与点A关于原点O对称,则点C的坐标是(1,﹣2);
(3)设反比例函数解析式为y=,
把B(2,3)代入得:k=6,
∴反比例函数解析式为y=;
(4)设一次函数解析式为y=mx+n,
把A(﹣1,2)与C(1,﹣2)代入得:,
解得:,
则一次函数解析式为y=﹣2x.
故答案为:(1)(2,3);(2)(1,﹣2);(3)y=;(4)y=﹣2x.
24.解:(1)∵x﹣1≠0,
∴x≠1,
故答案为x≠1;
(2)把(﹣1,﹣2)(0,﹣5)代入y=+m得,
解得m=1,k=6,
故答案为6,1;
画出函数图象如图所示:
(3)由图象可得,当x>1时,y随x的增大而减小(答案不唯一),
故答案为当x>1时,y随x的增大而减小(答案不唯一);
(4)由y=2x﹣5可知,当x=0时,y=﹣5,当x=4时,y=3,
∴直线y=2x﹣5经过点(0,﹣5),(4,3),
∵点(0,﹣5),(4,3)在函数y=+m的图象上,
∵直线y=2x﹣5与函数y=+m的图象的交点为(0,﹣5),(4,3),
由图象可得,不等式>﹣m+2x﹣5的解集x<0或1<x<4.
25.解:(1)将点A(2,4)代入y=,得:m=8,
则反比例函数解析式为y=,
当x=﹣4时,y=﹣2,
则点B(﹣4,﹣2),
将点A(2,4)、B(﹣4,﹣2)代入y=kx+b,
得:,
解得:,
则一次函数解析式为y=x+2;
(2)由题意知BC=2,
则△ACB的面积=×2×6=6.
26.解:(1)y=不是反比例函数.
(2)∵y=,
∴xy=.
∴y=,是反比例函数.
(3)∵xy=6,
∴y=,是反比例函数.
(4)∵3x+y=0,
∴y=﹣3x,不是反比例函数.
(5)∵x﹣2y=1,
∴2y=x﹣1.
∴y=x﹣,不是反比例函数.
(6)∵3xy+2=0,
∴xy=﹣.
∴y=,是反比例函数.
27.解:(1)∵点A(0,4),B(﹣3,0),
∴OA=4,OB=3,
∴AB=5,
∵四边形ABCD是菱形,
∴AD=5,
即点D的横坐标是5,
∴点D的坐标为(5,4),
∴4=,得k=20,
故答案为:20;
(2)∵四边形ABMN是平行四边形,∴AN∥BM,AN=BM,
∴AN可以看作是BM经过平移得到的,
首先BM向右平移了3个单位长度,
∴N点的横坐标为3,代入y=,得点N的纵坐标为y=,
∴M点的纵坐标为﹣4=,
∴M点的坐标为(0,).
