2021-2022学年鲁教五四新版六年级上册数学《第1章 丰富的图形世界》单元测试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年鲁教五四新版六年级上册数学《第1章 丰富的图形世界》单元测试卷(word版含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 250.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 00:00:00 | ||
图片预览

文档简介
2021-2022学年鲁教五四新版六年级上册数学《第1章
丰富的图形世界》单元测试卷
一.选择题
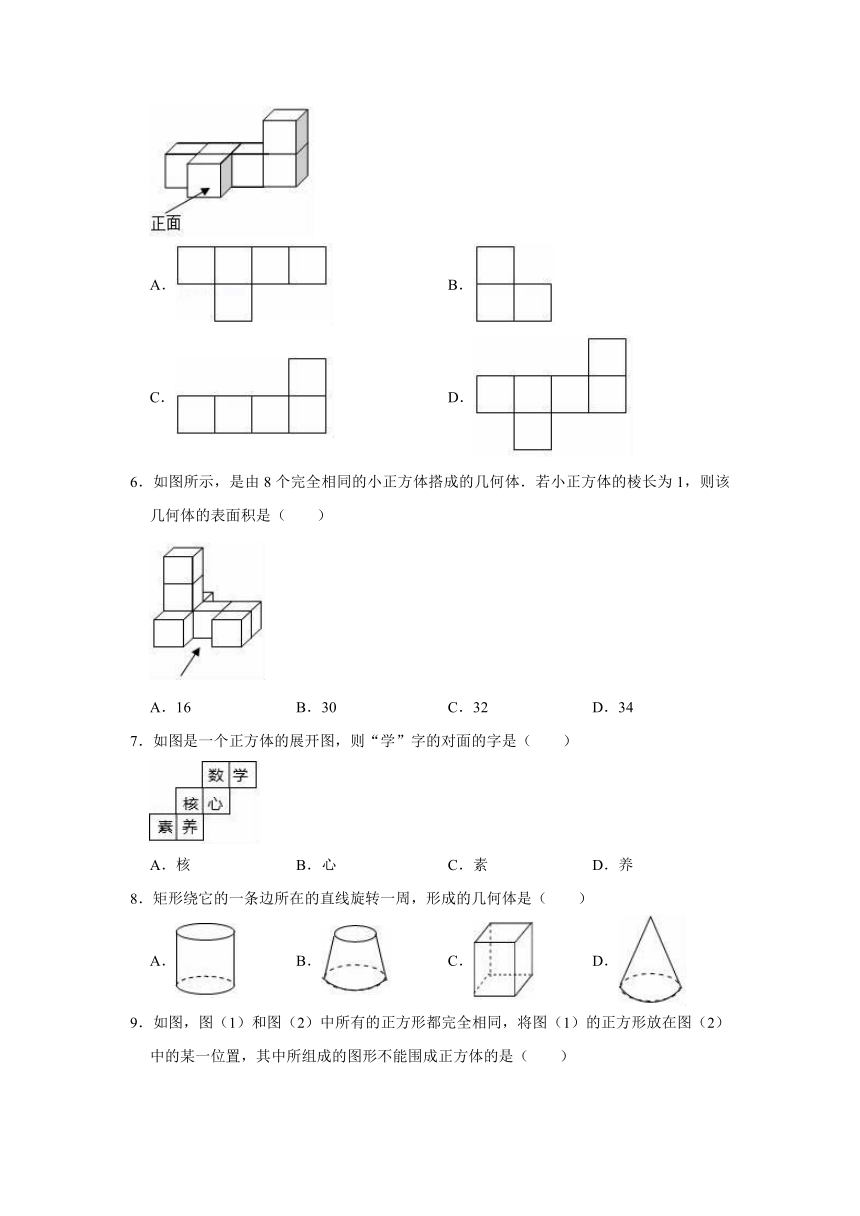
1.三棱柱的顶点个数是( )
A.3
B.4
C.5
D.6
2.如图所示的正方体沿某些棱展开后,能得到的平面图形是( )
A.
B.
C.
D.
3.用平面去截下列几何体,能截得长方形、三角形、等腰梯形三种形状的截面,这个几何体是( )
A.
B.
C.
D.
4.下列立体图形中,主视图和左视图不一样的是( )
A.
B.
C.
D.
5.如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
A.
B.
C.
D.
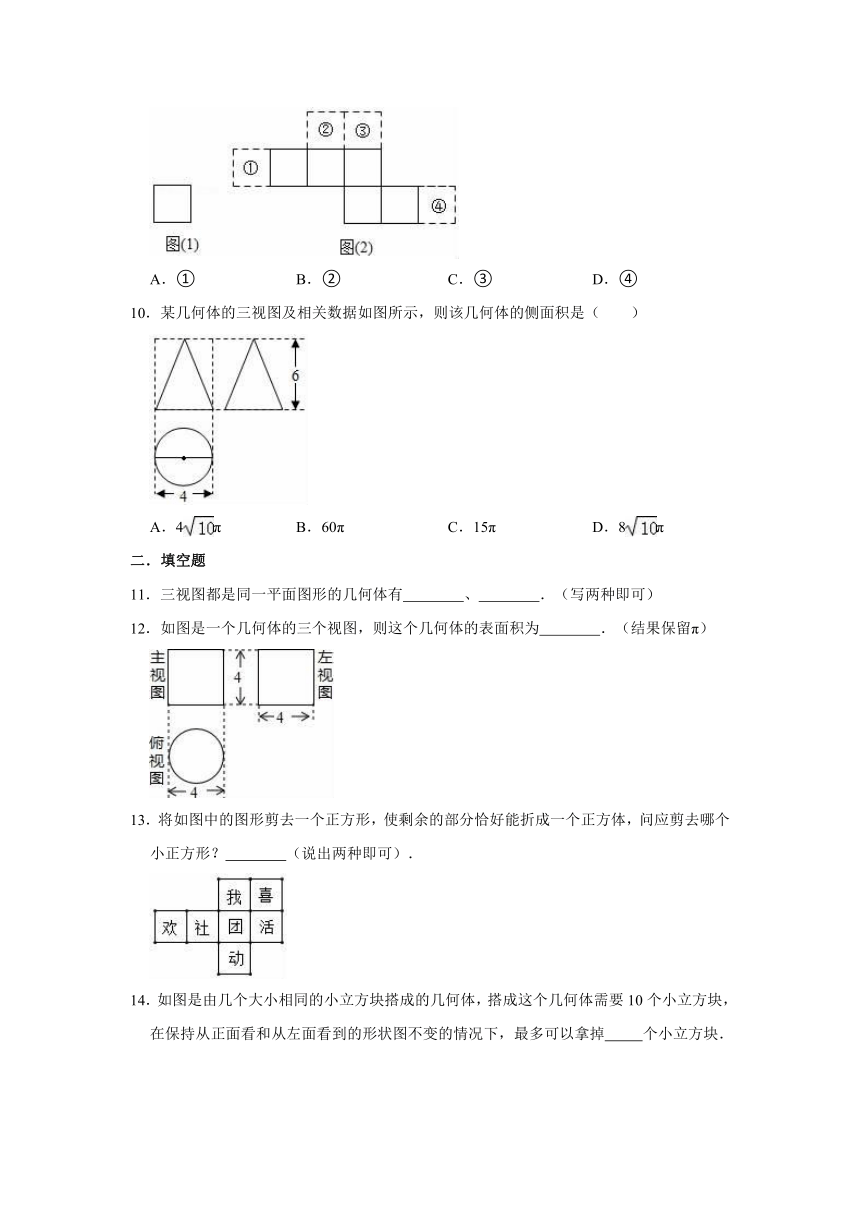
6.如图所示,是由8个完全相同的小正方体搭成的几何体.若小正方体的棱长为1,则该几何体的表面积是( )
A.16
B.30
C.32
D.34
7.如图是一个正方体的展开图,则“学”字的对面的字是( )
A.核
B.心
C.素
D.养
8.矩形绕它的一条边所在的直线旋转一周,形成的几何体是( )
A.
B.
C.
D.
9.如图,图(1)和图(2)中所有的正方形都完全相同,将图(1)的正方形放在图(2)中的某一位置,其中所组成的图形不能围成正方体的是( )
A.①
B.②
C.③
D.④
10.某几何体的三视图及相关数据如图所示,则该几何体的侧面积是( )
A.4π
B.60π
C.15π
D.8π
二.填空题
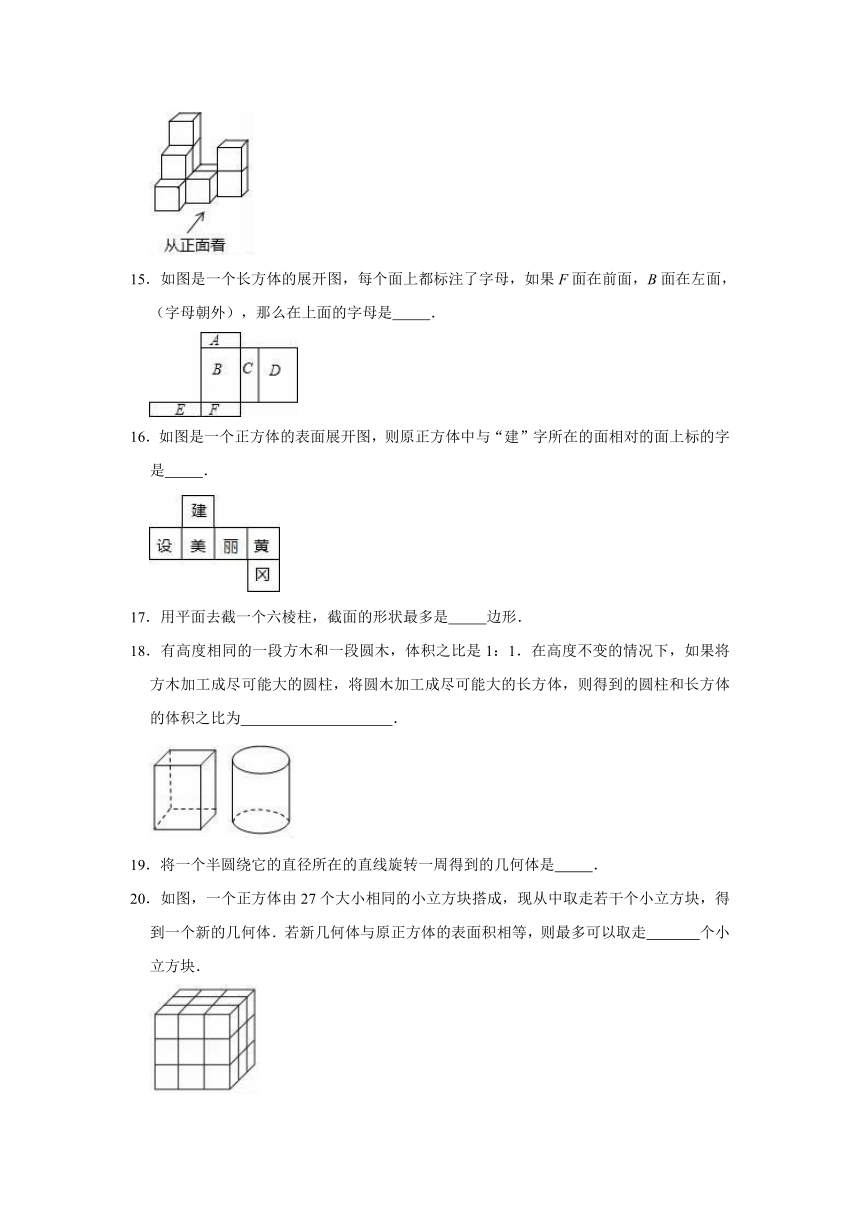
11.三视图都是同一平面图形的几何体有
、
.(写两种即可)
12.如图是一个几何体的三个视图,则这个几何体的表面积为
.(结果保留π)
13.将如图中的图形剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去哪个小正方形?
(说出两种即可).
14.如图是由几个大小相同的小立方块搭成的几何体,搭成这个几何体需要10个小立方块,在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉
个小立方块.
15.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是
.
16.如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是
.
17.用平面去截一个六棱柱,截面的形状最多是
边形.
18.有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为
.
19.将一个半圆绕它的直径所在的直线旋转一周得到的几何体是
.
20.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走
个小立方块.
三.解答题
21.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
22.如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?
23.如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.
24.指出下列平面图形是什么几何体的展开图.
25.若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
26.把一根长1.5米的圆柱形钢材截成三段后,如图,表面积比原来增加8平方米,这根钢材原来的体积是多少?
27.如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的体积:
cm3.
参考答案与试题解析
一.选择题
1.解:一个直三棱柱由两个三边形的底面和3个长方形的侧面组成,根据其特征及欧拉公式V+F﹣E=2可知,
它有6个顶点,
故选:D.
2.解:由正方体展开图的特征及正方形上的三种图形相邻,可得正方体沿某些棱展开后,能得到的平面图形是B.
故选:B.
3.解:圆台的截面不能得到长方形;
圆锥的截面不能得到长方形;
圆柱的截面不能得到等腰梯形;
当截面经过正方体的3个面时,得到三角形,
当截面与正方体的一个面平行时得到长方形,
当截面经过正方体的一个正方形的对角的顶点,经过4个面,又与对面斜交时,可得到等腰梯形,
故选:D.
4.解:A、圆柱的主视图和左视图均为全等的长方形,不符合题意;
B、圆锥的主视图和左视图均为全等的等腰三角形,不符合题意;
C、正方体的主视图和左视图均为全等的正方形,不符合题意;
D、这个三棱柱的主视图是正方形,左视图是三角形,符合题意;
故选:D.
5.解:从上面看,得到的视图是:,
故选:A.
6.解:根据小正方体的棱长为1,可知小正方体的一个面面积为1.从图中数出几何体的面为:34.
所以面积为:34.
故选:D.
7.解:这是一个正方体的平面展开图,共有六个面,其中面“数”与“养”相对,面“学”与面“核”相对,“心”与面“素”相对.
故选:A.
8.解:矩形绕它的一条边所在的直线旋转一周,形成的几何体是圆柱,
故选:A.
9.解:根据正方体的展开图的特征,11种情况中,“1﹣4﹣1型”6种,“2﹣3﹣1型”3种,“2﹣2﹣2型”1种,“3﹣3型”1种,
再根据“一线不过四、田凹应弃之”可得,只有放在①处,不能围成正方体,
故选:A.
10.解:观察图形可知:
圆锥母线长为:=2,
所以圆锥侧面积为:πrl=2×2×π=4π.
故选:A.
二.填空题
11.解:依题意,主视图、左视图以及俯视图都相同的几何体是正方体或球体.
故答案为:正方体、球体.
12.解:∵圆柱的直径为4,高为4,
∴表面积=2π×(×4)×4+π×(×4)2×2=24π.
故答案为:24π.
13.解:根据有“田”字格的展开图都不是正方体的表面展开图可知,故应剪去我或喜或活,
故答案为:我,喜.
14.解:如图所示:
在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉1个小立方块.
故答案为:1.
15.解:由组成几何体面之间的关系,得
F、B、C是邻面,F、B、E是邻面.
由F面在前面,B面在左面,得
C面在上,E面在下,
故答案为:C.
16.解:由正方体的展开图特点可得:“建”和“冈”相对;“设”和“丽”相对;“美”和“黄”相对;
故答案为:冈.
17.解:∵用平面去截六棱柱时最多与8个面相交得八边形,
∴最多可以截出八边形.
故答案是:八.
18.解:(1)如图:
设圆的半径为r,圆的面积与正方形的面积比是:(πr2):(2r×2r)=,
(2)如图:
设圆的半径为r,正方形的面积与圆的面积比是:
(2r×r):(π×r2)=,
因为,方木与圆木的体积和高度都相等,说明底面积也相等,即图(1)的大正方形面积等于图(二)的大圆的面积,
所以,现在的圆柱体积和长方体的体积的比值是:
:=.
答:圆柱体积和长方体的体积的比值为.
故答案为:.
19.解:将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球,
故答案为:球
20.解:若新几何体与原正方体的表面积相等,最多可以取走16个小正方体,只需留11个:①正中心的3个和四角上各2个,如图所示;②其中一个角3个,其余三个角和中心是2个(图略).
故答案为:16.
三.解答题
21.解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π?()2?x=π?()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
22.解:每块木料的上下底面的面积为:2××π×22=2π(dm2),
侧面的面积为:(×2π×2+2+2)×6=6π+24(dm2),
故每块木料的表面积是:2π+6π+24=8π+24(dm2).
答:柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是(8π+24)平方分米.
23.解:连线如下:
24.解:从左向右依次为:长方体;圆锥;圆柱.
25.解:这是一个正方体的平面展开图,共有六个面,
其中面“z”与面“3”相对,面“y”与面“﹣2”相对,“x”与面“10”相对.
则z+3=5,y+(﹣2)=5,x+10=5,
解得z=2,y=7,x=﹣5.
故x+y+z=4.
26.解:8÷4=2(平方米),
2×1.5=3(立方米).
答:这根钢材原来的体积为3立方米.
27.解:(1)拼图存在问题,如图:
(2)折叠而成的长方体的体积为:3×2×2=12(cm3).
故答案为:12.
丰富的图形世界》单元测试卷
一.选择题
1.三棱柱的顶点个数是( )
A.3
B.4
C.5
D.6
2.如图所示的正方体沿某些棱展开后,能得到的平面图形是( )
A.
B.
C.
D.
3.用平面去截下列几何体,能截得长方形、三角形、等腰梯形三种形状的截面,这个几何体是( )
A.
B.
C.
D.
4.下列立体图形中,主视图和左视图不一样的是( )
A.
B.
C.
D.
5.如图所示的几何体是由几个大小相同的小正方体搭成的,其俯视图是( )
A.
B.
C.
D.
6.如图所示,是由8个完全相同的小正方体搭成的几何体.若小正方体的棱长为1,则该几何体的表面积是( )
A.16
B.30
C.32
D.34
7.如图是一个正方体的展开图,则“学”字的对面的字是( )
A.核
B.心
C.素
D.养
8.矩形绕它的一条边所在的直线旋转一周,形成的几何体是( )
A.
B.
C.
D.
9.如图,图(1)和图(2)中所有的正方形都完全相同,将图(1)的正方形放在图(2)中的某一位置,其中所组成的图形不能围成正方体的是( )
A.①
B.②
C.③
D.④
10.某几何体的三视图及相关数据如图所示,则该几何体的侧面积是( )
A.4π
B.60π
C.15π
D.8π
二.填空题
11.三视图都是同一平面图形的几何体有
、
.(写两种即可)
12.如图是一个几何体的三个视图,则这个几何体的表面积为
.(结果保留π)
13.将如图中的图形剪去一个正方形,使剩余的部分恰好能折成一个正方体,问应剪去哪个小正方形?
(说出两种即可).
14.如图是由几个大小相同的小立方块搭成的几何体,搭成这个几何体需要10个小立方块,在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉
个小立方块.
15.如图是一个长方体的展开图,每个面上都标注了字母,如果F面在前面,B面在左面,(字母朝外),那么在上面的字母是
.
16.如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是
.
17.用平面去截一个六棱柱,截面的形状最多是
边形.
18.有高度相同的一段方木和一段圆木,体积之比是1:1.在高度不变的情况下,如果将方木加工成尽可能大的圆柱,将圆木加工成尽可能大的长方体,则得到的圆柱和长方体的体积之比为
.
19.将一个半圆绕它的直径所在的直线旋转一周得到的几何体是
.
20.如图,一个正方体由27个大小相同的小立方块搭成,现从中取走若干个小立方块,得到一个新的几何体.若新几何体与原正方体的表面积相等,则最多可以取走
个小立方块.
三.解答题
21.在一个底面直径为5cm,高为16cm圆柱形瓶内装满水,再将瓶内的水倒入一个底面直径为6cm,高为10cm的圆柱形玻璃杯中,能否完全装下?若装不下,求瓶内水面还有多高?若未能装满,求玻璃杯内水面离杯口的距离?
22.如图,把一根底面半径为2dm,高为6dm的圆柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是多少平方分米?
23.如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.
24.指出下列平面图形是什么几何体的展开图.
25.若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和为5,求x+y+z的值.
26.把一根长1.5米的圆柱形钢材截成三段后,如图,表面积比原来增加8平方米,这根钢材原来的体积是多少?
27.如图,小华用若干个正方形和长方形准备拼成一个长方体的展开图.拼完后,小华看来看去总觉得所拼图形似乎存在问题.
(1)请你帮小华分析一下拼图是否存在问题:若有多余块,则把图中多余部分涂黑;若还缺少,则直接在原图中补全;
(2)若图中的正方形边长为2cm,长方形的长为3cm,宽为2cm,请直接写出修正后所折叠而成的长方体的体积:
cm3.
参考答案与试题解析
一.选择题
1.解:一个直三棱柱由两个三边形的底面和3个长方形的侧面组成,根据其特征及欧拉公式V+F﹣E=2可知,
它有6个顶点,
故选:D.
2.解:由正方体展开图的特征及正方形上的三种图形相邻,可得正方体沿某些棱展开后,能得到的平面图形是B.
故选:B.
3.解:圆台的截面不能得到长方形;
圆锥的截面不能得到长方形;
圆柱的截面不能得到等腰梯形;
当截面经过正方体的3个面时,得到三角形,
当截面与正方体的一个面平行时得到长方形,
当截面经过正方体的一个正方形的对角的顶点,经过4个面,又与对面斜交时,可得到等腰梯形,
故选:D.
4.解:A、圆柱的主视图和左视图均为全等的长方形,不符合题意;
B、圆锥的主视图和左视图均为全等的等腰三角形,不符合题意;
C、正方体的主视图和左视图均为全等的正方形,不符合题意;
D、这个三棱柱的主视图是正方形,左视图是三角形,符合题意;
故选:D.
5.解:从上面看,得到的视图是:,
故选:A.
6.解:根据小正方体的棱长为1,可知小正方体的一个面面积为1.从图中数出几何体的面为:34.
所以面积为:34.
故选:D.
7.解:这是一个正方体的平面展开图,共有六个面,其中面“数”与“养”相对,面“学”与面“核”相对,“心”与面“素”相对.
故选:A.
8.解:矩形绕它的一条边所在的直线旋转一周,形成的几何体是圆柱,
故选:A.
9.解:根据正方体的展开图的特征,11种情况中,“1﹣4﹣1型”6种,“2﹣3﹣1型”3种,“2﹣2﹣2型”1种,“3﹣3型”1种,
再根据“一线不过四、田凹应弃之”可得,只有放在①处,不能围成正方体,
故选:A.
10.解:观察图形可知:
圆锥母线长为:=2,
所以圆锥侧面积为:πrl=2×2×π=4π.
故选:A.
二.填空题
11.解:依题意,主视图、左视图以及俯视图都相同的几何体是正方体或球体.
故答案为:正方体、球体.
12.解:∵圆柱的直径为4,高为4,
∴表面积=2π×(×4)×4+π×(×4)2×2=24π.
故答案为:24π.
13.解:根据有“田”字格的展开图都不是正方体的表面展开图可知,故应剪去我或喜或活,
故答案为:我,喜.
14.解:如图所示:
在保持从正面看和从左面看到的形状图不变的情况下,最多可以拿掉1个小立方块.
故答案为:1.
15.解:由组成几何体面之间的关系,得
F、B、C是邻面,F、B、E是邻面.
由F面在前面,B面在左面,得
C面在上,E面在下,
故答案为:C.
16.解:由正方体的展开图特点可得:“建”和“冈”相对;“设”和“丽”相对;“美”和“黄”相对;
故答案为:冈.
17.解:∵用平面去截六棱柱时最多与8个面相交得八边形,
∴最多可以截出八边形.
故答案是:八.
18.解:(1)如图:
设圆的半径为r,圆的面积与正方形的面积比是:(πr2):(2r×2r)=,
(2)如图:
设圆的半径为r,正方形的面积与圆的面积比是:
(2r×r):(π×r2)=,
因为,方木与圆木的体积和高度都相等,说明底面积也相等,即图(1)的大正方形面积等于图(二)的大圆的面积,
所以,现在的圆柱体积和长方体的体积的比值是:
:=.
答:圆柱体积和长方体的体积的比值为.
故答案为:.
19.解:将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球,
故答案为:球
20.解:若新几何体与原正方体的表面积相等,最多可以取走16个小正方体,只需留11个:①正中心的3个和四角上各2个,如图所示;②其中一个角3个,其余三个角和中心是2个(图略).
故答案为:16.
三.解答题
21.解:设将瓶内的水倒入一个底面直径是6cm,高是10cm的圆柱形玻璃杯中时,水面高为xcm,
根据题意得π?()2?x=π?()2×16,
解得x=,
∵>10,
∴不能完全装下.
﹣10=(cm),
16×=1.6(cm),
答:装不下,那么瓶内水面还有1.6cm.
22.解:每块木料的上下底面的面积为:2××π×22=2π(dm2),
侧面的面积为:(×2π×2+2+2)×6=6π+24(dm2),
故每块木料的表面积是:2π+6π+24=8π+24(dm2).
答:柱形木料沿相互垂直的两条直径锯成大小相等的4块,每块木料的表面积是(8π+24)平方分米.
23.解:连线如下:
24.解:从左向右依次为:长方体;圆锥;圆柱.
25.解:这是一个正方体的平面展开图,共有六个面,
其中面“z”与面“3”相对,面“y”与面“﹣2”相对,“x”与面“10”相对.
则z+3=5,y+(﹣2)=5,x+10=5,
解得z=2,y=7,x=﹣5.
故x+y+z=4.
26.解:8÷4=2(平方米),
2×1.5=3(立方米).
答:这根钢材原来的体积为3立方米.
27.解:(1)拼图存在问题,如图:
(2)折叠而成的长方体的体积为:3×2×2=12(cm3).
故答案为:12.
