人教版高中物理选修2-2 1.5 刚体平衡的条件 课件(41张PPT)
文档属性
| 名称 | 人教版高中物理选修2-2 1.5 刚体平衡的条件 课件(41张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-07-09 17:00:05 | ||
图片预览










文档简介
导入新课
严格地说,任何物体在力的作用下,都会产生变形.
但是,在正常情况下,工程实际中许多物体的变形都非常微小,如
建筑物中的梁
1.5 刚体平衡的条件
第一章 物体的平衡
1. 知识与能力
认识刚体的平衡条件
2 . 过程与方法
能用刚体的平衡条件分析物体的平衡
教学目标
3. 情感态度与价值观
培养全面分析问题的能力和推理能力
1、刚体的概念
2、刚体平衡的条件
能正确运用平衡条件求解静力学问题
教学重难点
重点
难点
2﹑例题详解
1﹑刚体平衡的条件
本节导航
1、刚体平衡的条件
A
D
B
C
图1.5-1
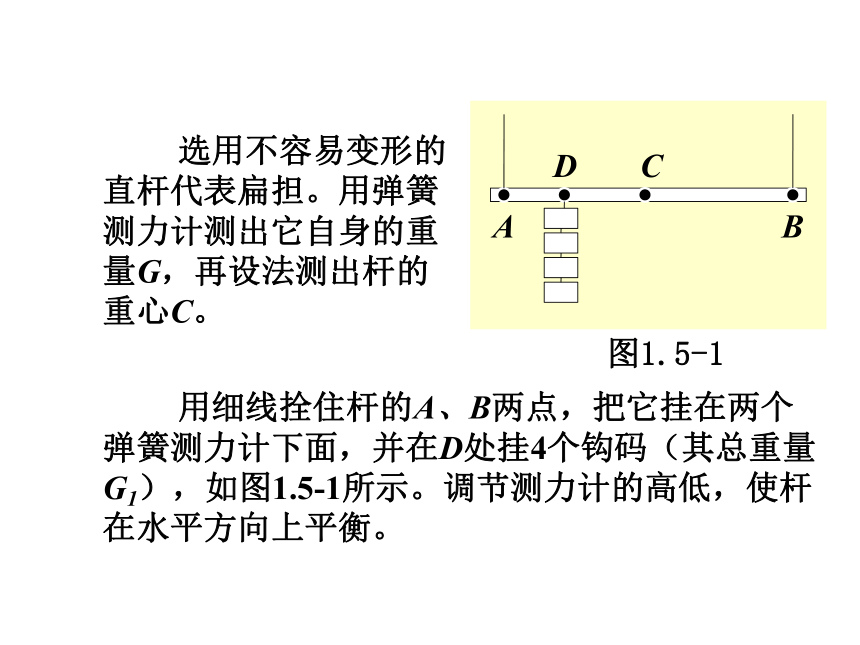
选用不容易变形的直杆代表扁担。用弹簧测力计测出它自身的重量G,再设法测出杆的重心C。
用细线拴住杆的A、B两点,把它挂在两个弹簧测力计下面,并在D处挂4个钩码(其总重量G1),如图1.5-1所示。调节测力计的高低,使杆在水平方向上平衡。
分别读出两个测力计的读数F1和F2。用刻度尺分别测出A、B、C、D间的距离。分析此时杆的受力情况。
画出直杆的受力分析示意图(如图1.5-2)
A
D
B
C
F1
G1
F2
G
图1.5-2
从实验数据可以看出,
F1 + F2 = G + G1
或
F1 + F2 – G – G1 = 0
A
D
B
C
F1
G1
F2
G
图1.5-2
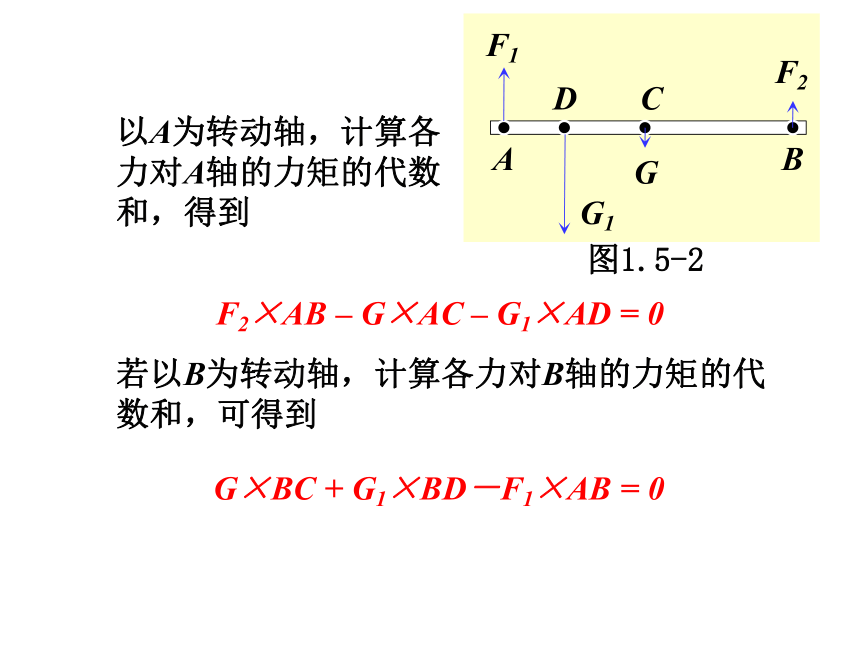
以A为转动轴,计算各力对A轴的力矩的代数和,得到
F2×AB – G×AC – G1×AD = 0
若以B为转动轴,计算各力对B轴的力矩的代数和,可得到
G×BC + G1×BD-F1×AB = 0
刚体平衡的条件是
合力为零、合力矩为零
即
ΣF = 0 和 ΣM = 0
2、例题详解
例题
为了称重汽车的重量,把汽车的前轮压在地秤上(图1.5-3甲),测得的结果为6.7×103N,汽车前后轮之间的距离是2.7m,汽车的重心距离后轮1.5m,求汽车的重量和后轮对地面的压力。
G
F1
F2
l
L
前轮
后轮
乙
图1.5-3
甲
分析
汽车可以看做刚体,处于平衡状态。受到重力G,地秤对前轮支持力F1和地面对后轮支持力F2的作用,如图1.5-3乙。
G
F1
F2
l
L
前轮
后轮
乙
图1.5-3
甲
根据刚体平衡条件,这三个力的合力为零;若将后轮与地面的接触位置作为转动轴,则汽车受到两个力矩的作用:一个是重力G的力矩,另一个是地秤对前轮支持力F1的力矩,F1的大小等于汽车前轮压地秤的力,即题中所给的测量结果6.7×103N,这两个力矩的合力矩也为零。
解
汽车处于平衡状态,选汽车后轮与地面接触的位置为转动轴,合力矩为
G×l – F1×L = 0
由此可得
G = = N= 1.2 ×104N
F1 ×L
l
6.7 ×103 ×2.7
l
即汽车的重量为1.2 ×104N。
再由合力为零,得
F2 = G – F1 = (1.2 ×104 – 6.7 ×103)N = 5.3 ×103N
据牛顿第三定律,后轮对地面的压力大小为
5.3 ×103N
例题
塔式起重机如图1.5-4所示。机架重P = 700kN,重力作用线通过塔架中心。最大起重量G = 200kN,最大悬臂长为12m,轨道AB的间距为4m。平衡块重W,到机身中心线距离为6m,试问:
图1.5-4
W
G
FA
FB
(1)为保证起重机在满载和空载时都不致翻倒,平衡块的重量W应为多少?
(2)若平衡块重W = 180kN,当满载时轨道A、B给起重机轮子的作用力各为多少?
分析
要使起重机不翻倒,应使作用在起重机上的所有力的力矩满足平衡条件。取起重机为研究对象,起重机所受的力有:
被吊物体所受的重力G
机架所受的重力P
平衡块所受的重力W
以及轨道A、B给起重机轮子的作用力FA和FB
图1.5-4
W
G
FA
FB
解
(1)满载时,为了保证起重机不致绕B点翻倒,这些力的力矩必须满足平衡方程ΣMB = 0,即所有外力对B点的力矩之和为零。在临界情况下,FA = 0,这时求出的W值是允许的最小值。由ΣMB = 0得
即
Wmin =
= kN
= 75kN
10G – 2P
8
10×200-2×700
8
Wmin×(6 + 2) + P ×2 - G ×(12 - 2) = 0
(1)
空载时G = 0,为了保证起重机不致绕A点翻倒,所受力的力矩必须满足平衡方程ΣMA = 0,即所有外力对A点的力矩之和为零。在临界情况下,FB = 0,这时求出的W值是所允许的最大值。由ΣMA = 0 ,得
Wmax×(6-2)-P×2 = 0
即
Wmax =
= kN
= 350kN
2P
4
2×700
4
(2)
要使起重机不翻倒,平衡块的重量应在这两者之间。
即75kN < W < 350kN
(2)取W = 180kN,满载时轮子轨道A、B给起重机的作用力为FA和FB。此时,起重机在力G、P、W以及FA和FB的作用下平衡。根据刚体的平衡条件
ΣF = 0
– W – P – G + FA + FB = 0
(3)
取A点为转动轴,有
ΣMA = 0
W×(6 – 2) – P×2 – G×(12 + 2) + FB×4 = 0
(4)
代入(3)式得FA = 210N
由(4)式可得FB = = 870N
14G + 2P – 4W
4
课堂小结
1、在任何外力作用下,大小和形状不变的物体,称为刚体(rigid body).
2、刚体平衡的条件是合力为零、合力矩为零。即
ΣF = 0 和 ΣM = 0
高 考 链 接
1、(1997年全国高考题)如图所示,重物的质量为m,轻细绳AO与BO的A端、B端是固定的,平衡时AO是水平的,BO与水平面夹角为θ,AO的拉力F1和BO的拉力F2的大小是( )
A、F1 = mgcos θ
B、F1 = mgcot θ
C、F2 = mgsin θ
D、F2 = mg/sin θ
A
B
O
θ
解析
选O点为研究对象,O点受3个力的作用。沿水平方向和竖直方向建立 坐标系,如图所示。由物体的平衡条件
O
F1
F2
x
y
θ
Fx合 = F2cosθ – F1 = 0;
Fy合 = F2sinθ – mg = 0
解得:F1 = mgcotθ; F2 = mg/sinθ
因此选项BD正确
A
B
L
图12
d
2、(2001年津晋理综高考题)图12是轮船上悬挂救生艇的装置的简化示意图。A、B是船舷上的固定箍,以N1、N2分别表示固定箍A、B作用于吊杆的水平力的大小,已知救生艇所受的重力G=1500N,d=1m,L=0.8m。如吊杆的质量忽略不计,则( )
A.N1=1200N,N2=0 B.N1=0,N2=1200N
C.N1=750N,N2=750N D.N1=1200N,N2=1200N
解析
A
B
N1
N2
图13
NA
NB
T = G
隔离吊杆如图13,分析受力有:绳向下的拉力T,箍A对杆的水平作用力N1和竖直作用力NA,箍B对杆的水平作用力N2和竖直作用力NB。
选B为转动轴,由力矩平衡可得
N1· D = T ·L …………(1)
选A为转动轴,由力矩平衡可得
N2· D = T ·L …………(2)
联立(1)(2)解得 N1=1200N,N2=1200N
因此,本题的正确选项为D。
课 堂 练 习
1.如图1所示,ON杆可以在竖直平面内绕O点自由转动,若在N端分别沿图示方向施力F1、F2、F3,杆均能静止在图示位置上.则三力的大小关系是 ( )
A.F1=F2=F3 B.F1>F2>F3
C.F2>F1>F3 D.F1>F3>F2
D
2. 一段粗细不均匀的木棍如图2所示,支在某点恰好平衡,若在该处将木棍截成两段,则所分成两段的重量必定是 ( )
A.相等
B.细段轻、粗段重
C.细段重,粗段轻
D.不能确定
B
3. 如图3,把物体A放在水平板OB的正中央,用一不变的力F将板的B端匀速地慢慢抬高(O端不动),设A相对平板静止,则A对板的压力将______,A与B之间的摩擦力将______,F对O点的力矩将______.
减小
增大
减小
习题答案
1、左端压力变小,右端压力变大。
2、设棒长为L,离甲 处;离乙 处。
L
3
L
2
3、将圆木的一端放在地面上,另一端放在台秤上,读出数据。再将圆木反放,重复前面做法。两次数据之和等于圆木的重量。
严格地说,任何物体在力的作用下,都会产生变形.
但是,在正常情况下,工程实际中许多物体的变形都非常微小,如
建筑物中的梁
1.5 刚体平衡的条件
第一章 物体的平衡
1. 知识与能力
认识刚体的平衡条件
2 . 过程与方法
能用刚体的平衡条件分析物体的平衡
教学目标
3. 情感态度与价值观
培养全面分析问题的能力和推理能力
1、刚体的概念
2、刚体平衡的条件
能正确运用平衡条件求解静力学问题
教学重难点
重点
难点
2﹑例题详解
1﹑刚体平衡的条件
本节导航
1、刚体平衡的条件
A
D
B
C
图1.5-1
选用不容易变形的直杆代表扁担。用弹簧测力计测出它自身的重量G,再设法测出杆的重心C。
用细线拴住杆的A、B两点,把它挂在两个弹簧测力计下面,并在D处挂4个钩码(其总重量G1),如图1.5-1所示。调节测力计的高低,使杆在水平方向上平衡。
分别读出两个测力计的读数F1和F2。用刻度尺分别测出A、B、C、D间的距离。分析此时杆的受力情况。
画出直杆的受力分析示意图(如图1.5-2)
A
D
B
C
F1
G1
F2
G
图1.5-2
从实验数据可以看出,
F1 + F2 = G + G1
或
F1 + F2 – G – G1 = 0
A
D
B
C
F1
G1
F2
G
图1.5-2
以A为转动轴,计算各力对A轴的力矩的代数和,得到
F2×AB – G×AC – G1×AD = 0
若以B为转动轴,计算各力对B轴的力矩的代数和,可得到
G×BC + G1×BD-F1×AB = 0
刚体平衡的条件是
合力为零、合力矩为零
即
ΣF = 0 和 ΣM = 0
2、例题详解
例题
为了称重汽车的重量,把汽车的前轮压在地秤上(图1.5-3甲),测得的结果为6.7×103N,汽车前后轮之间的距离是2.7m,汽车的重心距离后轮1.5m,求汽车的重量和后轮对地面的压力。
G
F1
F2
l
L
前轮
后轮
乙
图1.5-3
甲
分析
汽车可以看做刚体,处于平衡状态。受到重力G,地秤对前轮支持力F1和地面对后轮支持力F2的作用,如图1.5-3乙。
G
F1
F2
l
L
前轮
后轮
乙
图1.5-3
甲
根据刚体平衡条件,这三个力的合力为零;若将后轮与地面的接触位置作为转动轴,则汽车受到两个力矩的作用:一个是重力G的力矩,另一个是地秤对前轮支持力F1的力矩,F1的大小等于汽车前轮压地秤的力,即题中所给的测量结果6.7×103N,这两个力矩的合力矩也为零。
解
汽车处于平衡状态,选汽车后轮与地面接触的位置为转动轴,合力矩为
G×l – F1×L = 0
由此可得
G = = N= 1.2 ×104N
F1 ×L
l
6.7 ×103 ×2.7
l
即汽车的重量为1.2 ×104N。
再由合力为零,得
F2 = G – F1 = (1.2 ×104 – 6.7 ×103)N = 5.3 ×103N
据牛顿第三定律,后轮对地面的压力大小为
5.3 ×103N
例题
塔式起重机如图1.5-4所示。机架重P = 700kN,重力作用线通过塔架中心。最大起重量G = 200kN,最大悬臂长为12m,轨道AB的间距为4m。平衡块重W,到机身中心线距离为6m,试问:
图1.5-4
W
G
FA
FB
(1)为保证起重机在满载和空载时都不致翻倒,平衡块的重量W应为多少?
(2)若平衡块重W = 180kN,当满载时轨道A、B给起重机轮子的作用力各为多少?
分析
要使起重机不翻倒,应使作用在起重机上的所有力的力矩满足平衡条件。取起重机为研究对象,起重机所受的力有:
被吊物体所受的重力G
机架所受的重力P
平衡块所受的重力W
以及轨道A、B给起重机轮子的作用力FA和FB
图1.5-4
W
G
FA
FB
解
(1)满载时,为了保证起重机不致绕B点翻倒,这些力的力矩必须满足平衡方程ΣMB = 0,即所有外力对B点的力矩之和为零。在临界情况下,FA = 0,这时求出的W值是允许的最小值。由ΣMB = 0得
即
Wmin =
= kN
= 75kN
10G – 2P
8
10×200-2×700
8
Wmin×(6 + 2) + P ×2 - G ×(12 - 2) = 0
(1)
空载时G = 0,为了保证起重机不致绕A点翻倒,所受力的力矩必须满足平衡方程ΣMA = 0,即所有外力对A点的力矩之和为零。在临界情况下,FB = 0,这时求出的W值是所允许的最大值。由ΣMA = 0 ,得
Wmax×(6-2)-P×2 = 0
即
Wmax =
= kN
= 350kN
2P
4
2×700
4
(2)
要使起重机不翻倒,平衡块的重量应在这两者之间。
即75kN < W < 350kN
(2)取W = 180kN,满载时轮子轨道A、B给起重机的作用力为FA和FB。此时,起重机在力G、P、W以及FA和FB的作用下平衡。根据刚体的平衡条件
ΣF = 0
– W – P – G + FA + FB = 0
(3)
取A点为转动轴,有
ΣMA = 0
W×(6 – 2) – P×2 – G×(12 + 2) + FB×4 = 0
(4)
代入(3)式得FA = 210N
由(4)式可得FB = = 870N
14G + 2P – 4W
4
课堂小结
1、在任何外力作用下,大小和形状不变的物体,称为刚体(rigid body).
2、刚体平衡的条件是合力为零、合力矩为零。即
ΣF = 0 和 ΣM = 0
高 考 链 接
1、(1997年全国高考题)如图所示,重物的质量为m,轻细绳AO与BO的A端、B端是固定的,平衡时AO是水平的,BO与水平面夹角为θ,AO的拉力F1和BO的拉力F2的大小是( )
A、F1 = mgcos θ
B、F1 = mgcot θ
C、F2 = mgsin θ
D、F2 = mg/sin θ
A
B
O
θ
解析
选O点为研究对象,O点受3个力的作用。沿水平方向和竖直方向建立 坐标系,如图所示。由物体的平衡条件
O
F1
F2
x
y
θ
Fx合 = F2cosθ – F1 = 0;
Fy合 = F2sinθ – mg = 0
解得:F1 = mgcotθ; F2 = mg/sinθ
因此选项BD正确
A
B
L
图12
d
2、(2001年津晋理综高考题)图12是轮船上悬挂救生艇的装置的简化示意图。A、B是船舷上的固定箍,以N1、N2分别表示固定箍A、B作用于吊杆的水平力的大小,已知救生艇所受的重力G=1500N,d=1m,L=0.8m。如吊杆的质量忽略不计,则( )
A.N1=1200N,N2=0 B.N1=0,N2=1200N
C.N1=750N,N2=750N D.N1=1200N,N2=1200N
解析
A
B
N1
N2
图13
NA
NB
T = G
隔离吊杆如图13,分析受力有:绳向下的拉力T,箍A对杆的水平作用力N1和竖直作用力NA,箍B对杆的水平作用力N2和竖直作用力NB。
选B为转动轴,由力矩平衡可得
N1· D = T ·L …………(1)
选A为转动轴,由力矩平衡可得
N2· D = T ·L …………(2)
联立(1)(2)解得 N1=1200N,N2=1200N
因此,本题的正确选项为D。
课 堂 练 习
1.如图1所示,ON杆可以在竖直平面内绕O点自由转动,若在N端分别沿图示方向施力F1、F2、F3,杆均能静止在图示位置上.则三力的大小关系是 ( )
A.F1=F2=F3 B.F1>F2>F3
C.F2>F1>F3 D.F1>F3>F2
D
2. 一段粗细不均匀的木棍如图2所示,支在某点恰好平衡,若在该处将木棍截成两段,则所分成两段的重量必定是 ( )
A.相等
B.细段轻、粗段重
C.细段重,粗段轻
D.不能确定
B
3. 如图3,把物体A放在水平板OB的正中央,用一不变的力F将板的B端匀速地慢慢抬高(O端不动),设A相对平板静止,则A对板的压力将______,A与B之间的摩擦力将______,F对O点的力矩将______.
减小
增大
减小
习题答案
1、左端压力变小,右端压力变大。
2、设棒长为L,离甲 处;离乙 处。
L
3
L
2
3、将圆木的一端放在地面上,另一端放在台秤上,读出数据。再将圆木反放,重复前面做法。两次数据之和等于圆木的重量。
