9.1(2)华师版七年级三角形的外角和
文档属性
| 名称 | 9.1(2)华师版七年级三角形的外角和 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-30 00:00:00 | ||
图片预览


文档简介
(共25张PPT)
三角形的外角和
福田九义校 陈康
2012\04\17
外角
相邻的内角
不相邻的内角
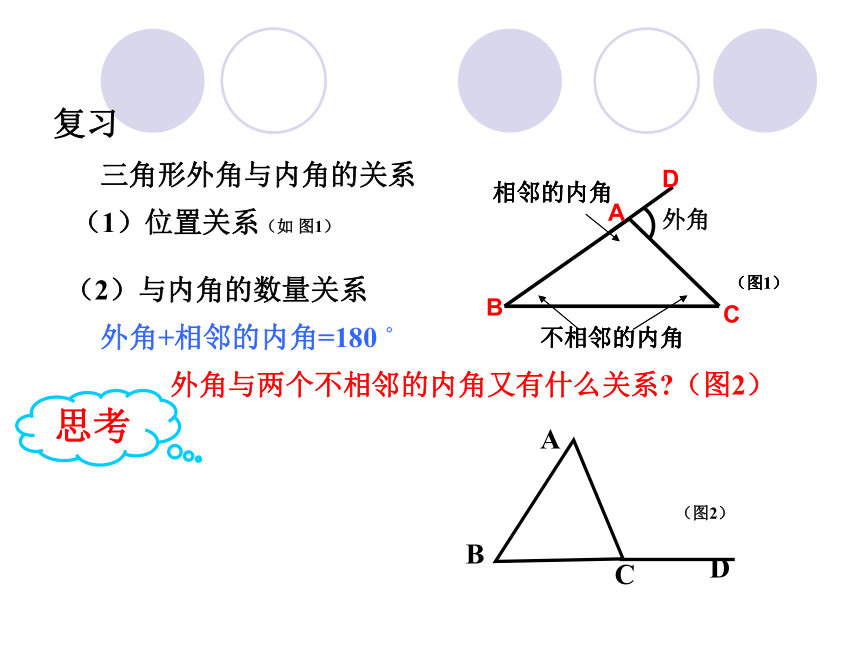
复习
三角形外角与内角的关系
(1)位置关系(如 图1)
(2)与内角的数量关系
外角+相邻的内角=180
外角与两个不相邻的内角又有什么关系 (图2)
(图1)
(图2)
思考
A
B
C
D
相邻的内角
不相邻的内角
(图1)
A
B
C
D
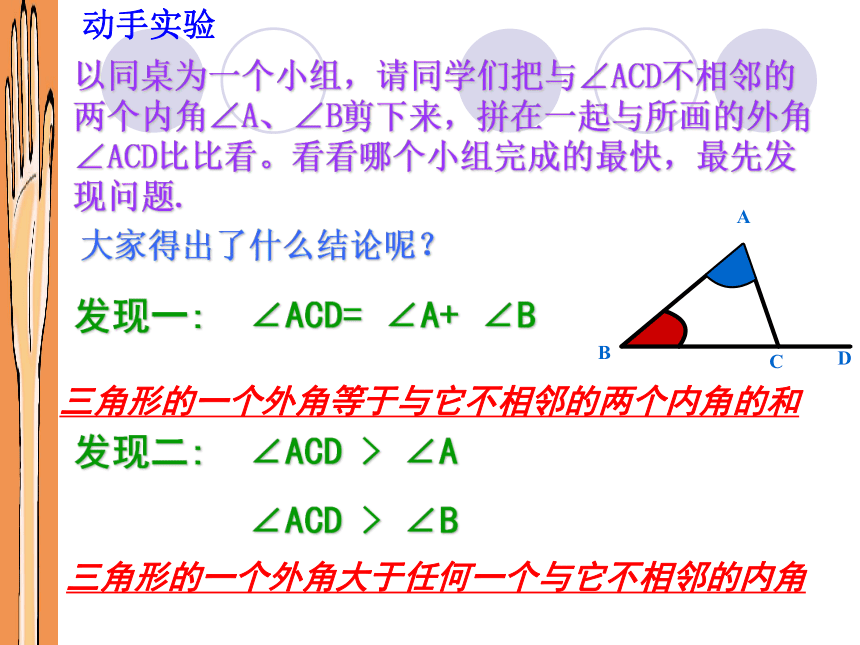
以同桌为一个小组,请同学们把与∠ACD不相邻的两个内角∠A、∠B剪下来,拼在一起与所画的外角∠ACD比比看。看看哪个小组完成的最快,最先发现问题.
大家得出了什么结论呢?
发现一: ∠ACD= ∠A+ ∠B
发现二: ∠ACD > ∠A
∠ACD > ∠B
动手实验
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角大于任何一个与它不相邻的内角
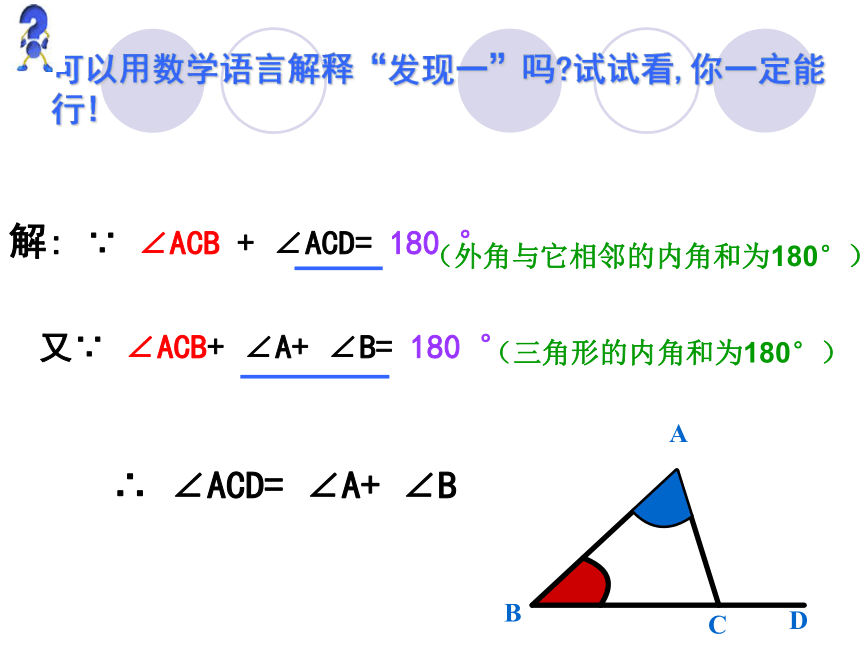
可以用数学语言解释“发现一”吗 试试看,你一定能行!
解: ∵ ∠ACB + ∠ACD= 180 °
又∵ ∠ACB+ ∠A+ ∠B= 180 °
∴ ∠ACD= ∠A+ ∠B
(外角与它相邻的内角和为180°)
(三角形的内角和为180°)
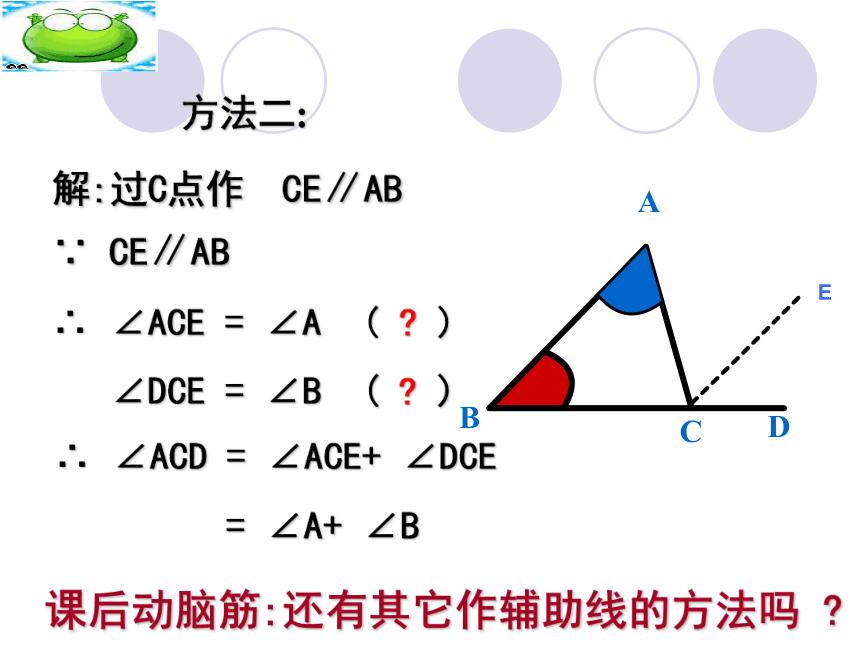
方法二:
解:过C点作 CE∥AB
∵ CE∥AB
∴ ∠ACE = ∠A ( )
∠DCE = ∠B ( )
∴ ∠ACD = ∠ACE+ ∠DCE
= ∠A+ ∠B
课后动脑筋:还有其它作辅助线的方法吗
E
三角形外角与内角之间的关系
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的
两个内角的和;
3、三角形的一个外角 任何一个与它
不相邻的内角。
等于
大于
互补
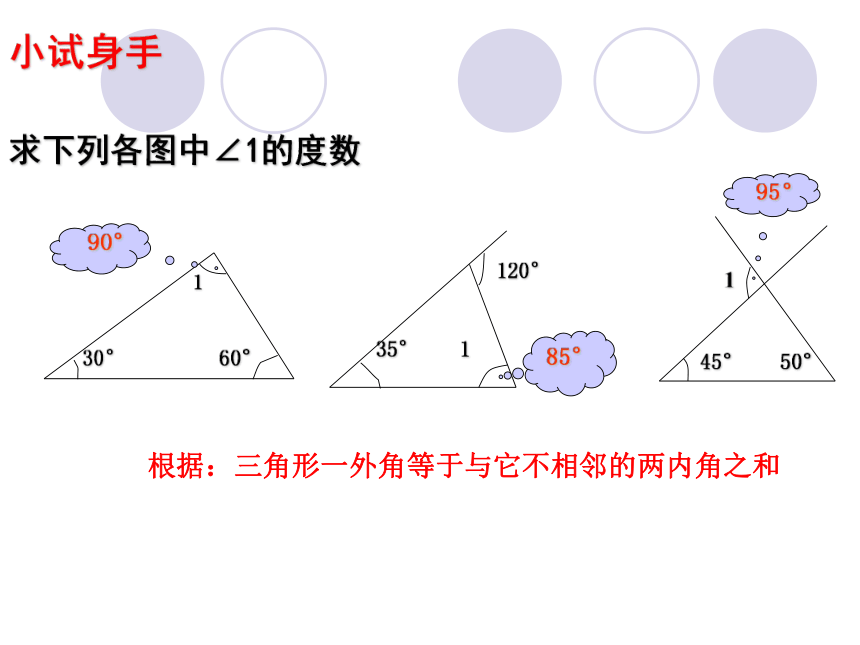
小试身手
求下列各图中∠1的度数
30°
60°
1
1
35°
120°
50°
45°
1
90°
85°
95°
根据:三角形一外角等于与它不相邻的两内角之和
三角形内角和是180 °
我们知道
三角形的外角和是多少呢
想一想
1.什么是三角形的外角和
2.三角形有固定外角和吗
3.如果有,三角形的外角和是多少呢
D
E
F
A
C
B
1
2
3
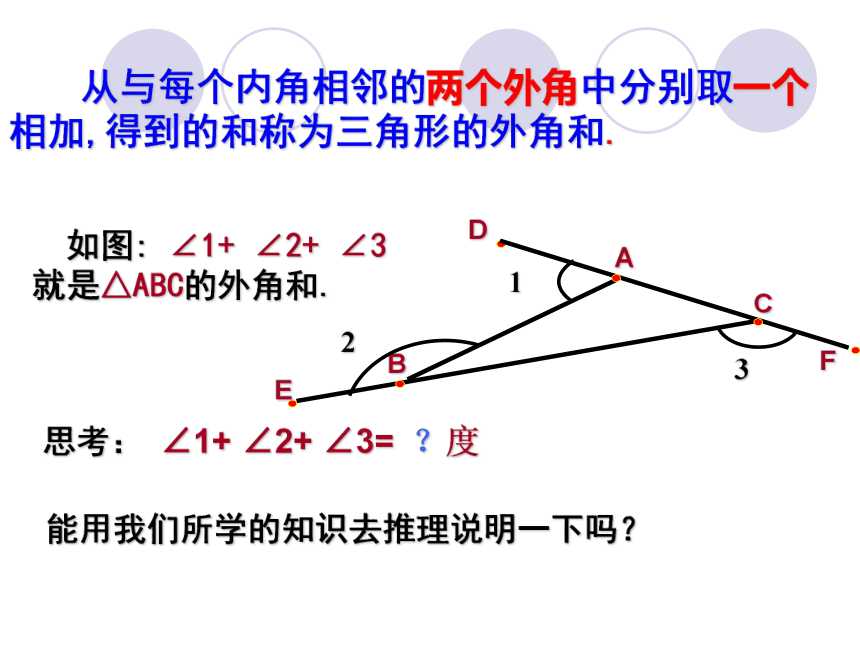
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图: ∠1+ ∠2+ ∠3就是△ABC的外角和.
思考: ∠1+ ∠2+ ∠3= ?度
能用我们所学的知识去推理说明一下吗?
做一做:
把三等式左右两边分别相加可以得到:
—— + —— + —— = —— (1)
而 (2)
比较(1)、(2),你能得出什么结论?
______
______
______
1
2
3
结论:三角形的外角和等于360度;
5400
三角形的外角和等于3600
让 我 们 展 开 想 象 的 翅 膀
例1 如图,D是△ABC的边BC上一点, ∠B=∠BAD, ∠ADC=80 , ∠BAC=70 . 求:
解 :(1)
∵ ∠ADC是⊿ABD的外角 (已知)
∴∠ADC=∠B+∠BAD=80
(三角形的一 个外角等于与它不相邻的两个内角的和)
又∵ ∠B=∠BAD
∴∠B=40
(2)
∵在⊿ABC中 ∠ B+ ∠ BAC+ ∠ C= 180
∴∠ C= 180 - ∠ B - ∠ BAC
= 180 -40 -70
=70
(三角形的内角和为180 )
(1) ∠ B的度数;(2) ∠ C的度数。
A
B
D
C
80
例 2
三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( )
A. 80 120 160 B. 160 120 80
C. 100 60 20 D. 140 120 100
解:设三角形的三个外角分别为2k,3k,4k,
根据三角形的外角和等于360 ,有
2k+3k+4k= 360 ,
可解得k=40 ,三个外角分别为80 120 160 ,
则相邻的内角分
别为100 60 20
故选 C
C
∠A+∠B+∠C+∠D+∠E+∠F= .
D
E
F
1
2
3
360°
N
P
M
C
B
A
F
C
B
A
3、动脑筋,想一想
1 三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角。
2 三角形的内角和等于180
三角形的外角和等于360
3 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
三角形的外角与它相邻的内角互补
如图,计算∠BOC
知识拓展
可要动脑哟
C
B
O
A
F
C
B
O
A
F
例3、
如图所示,在△ABC中,∠B=65°,∠C=45°,
AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的
度数。
解:
∠CAB=180°-∠C-∠B
=180°-45°-65°=70°
∵AE是∠BAC的角平分线,
∴∠BAE=
又∵在△ABC中,∠DAB=180°-∠ADB-∠B
=180°-90°-65°=25°
∴∠DAE=∠BAE-∠DAB=35°-25°=10°
例4、
如图1所示,点P是△ABC内一点,试说明∠A与
∠P的大小关系。
图1
图 2
解: 延长BP交AC于点E,如图2所示
∵∠BPC是△PEC的一个外角
∴∠BPC>∠PEC 又∵∠PEC是△ABE的一个外角
∴∠PEC>∠A
∴∠BPC>∠A,即∠P>∠A
1.判断∠1与∠3的大小,并说明理由。
解:∠3 > ∠1
∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1
2、如图:∠1=25°,
∠2=95°,∠3=30°,
则∠4=_______
A
D
E
C
B
1
4
3
2
30°
练一练
F
例5、
如图所示,在△ABC中,∠B=36°,∠ACB=110°,AE是
∠BAC的平分线,AD是BC边上的高,求∠DAE的大小。
解: ∵∠ACB+∠B+∠BAC=180°
∴∠BAC=180°-∠ACB-∠B
=180°-110°-36°=34°
∵AE平分∠BAC
∴
∵∠ACB=∠CAD+∠D ∴∠CAD=∠ACB-∠D
∵AD是BC边上的高 ∴∠D=90°
∴∠CAD=∠ACB-∠D=110°-90°=20°
∴∠DAE=∠EAC+∠CAD=17°+20°=37°
再 见
三角形的外角和
福田九义校 陈康
2012\04\17
外角
相邻的内角
不相邻的内角
复习
三角形外角与内角的关系
(1)位置关系(如 图1)
(2)与内角的数量关系
外角+相邻的内角=180
外角与两个不相邻的内角又有什么关系 (图2)
(图1)
(图2)
思考
A
B
C
D
相邻的内角
不相邻的内角
(图1)
A
B
C
D
以同桌为一个小组,请同学们把与∠ACD不相邻的两个内角∠A、∠B剪下来,拼在一起与所画的外角∠ACD比比看。看看哪个小组完成的最快,最先发现问题.
大家得出了什么结论呢?
发现一: ∠ACD= ∠A+ ∠B
发现二: ∠ACD > ∠A
∠ACD > ∠B
动手实验
三角形的一个外角等于与它不相邻的两个内角的和
三角形的一个外角大于任何一个与它不相邻的内角
可以用数学语言解释“发现一”吗 试试看,你一定能行!
解: ∵ ∠ACB + ∠ACD= 180 °
又∵ ∠ACB+ ∠A+ ∠B= 180 °
∴ ∠ACD= ∠A+ ∠B
(外角与它相邻的内角和为180°)
(三角形的内角和为180°)
方法二:
解:过C点作 CE∥AB
∵ CE∥AB
∴ ∠ACE = ∠A ( )
∠DCE = ∠B ( )
∴ ∠ACD = ∠ACE+ ∠DCE
= ∠A+ ∠B
课后动脑筋:还有其它作辅助线的方法吗
E
三角形外角与内角之间的关系
1、三角形的一个外角与它相邻的内角 ;
2、三角形的一个外角 与它不相邻的
两个内角的和;
3、三角形的一个外角 任何一个与它
不相邻的内角。
等于
大于
互补
小试身手
求下列各图中∠1的度数
30°
60°
1
1
35°
120°
50°
45°
1
90°
85°
95°
根据:三角形一外角等于与它不相邻的两内角之和
三角形内角和是180 °
我们知道
三角形的外角和是多少呢
想一想
1.什么是三角形的外角和
2.三角形有固定外角和吗
3.如果有,三角形的外角和是多少呢
D
E
F
A
C
B
1
2
3
从与每个内角相邻的两个外角中分别取一个相加,得到的和称为三角形的外角和.
如图: ∠1+ ∠2+ ∠3就是△ABC的外角和.
思考: ∠1+ ∠2+ ∠3= ?度
能用我们所学的知识去推理说明一下吗?
做一做:
把三等式左右两边分别相加可以得到:
—— + —— + —— = —— (1)
而 (2)
比较(1)、(2),你能得出什么结论?
______
______
______
1
2
3
结论:三角形的外角和等于360度;
5400
三角形的外角和等于3600
让 我 们 展 开 想 象 的 翅 膀
例1 如图,D是△ABC的边BC上一点, ∠B=∠BAD, ∠ADC=80 , ∠BAC=70 . 求:
解 :(1)
∵ ∠ADC是⊿ABD的外角 (已知)
∴∠ADC=∠B+∠BAD=80
(三角形的一 个外角等于与它不相邻的两个内角的和)
又∵ ∠B=∠BAD
∴∠B=40
(2)
∵在⊿ABC中 ∠ B+ ∠ BAC+ ∠ C= 180
∴∠ C= 180 - ∠ B - ∠ BAC
= 180 -40 -70
=70
(三角形的内角和为180 )
(1) ∠ B的度数;(2) ∠ C的度数。
A
B
D
C
80
例 2
三角形的三个外角之比为2:3:4,
则与它们相邻的内角分别为( )
A. 80 120 160 B. 160 120 80
C. 100 60 20 D. 140 120 100
解:设三角形的三个外角分别为2k,3k,4k,
根据三角形的外角和等于360 ,有
2k+3k+4k= 360 ,
可解得k=40 ,三个外角分别为80 120 160 ,
则相邻的内角分
别为100 60 20
故选 C
C
∠A+∠B+∠C+∠D+∠E+∠F= .
D
E
F
1
2
3
360°
N
P
M
C
B
A
F
C
B
A
3、动脑筋,想一想
1 三角形的外角性质:
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于任何一个与它不相邻的内角。
2 三角形的内角和等于180
三角形的外角和等于360
3 在求角的度数时,常可利用三角形的内角和及外角的性质来找数量关系;涉及图形时,可先把已知条件尽可能的在图中标出来,有助于直观分析题意。
三角形的外角与它相邻的内角互补
如图,计算∠BOC
知识拓展
可要动脑哟
C
B
O
A
F
C
B
O
A
F
例3、
如图所示,在△ABC中,∠B=65°,∠C=45°,
AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的
度数。
解:
∠CAB=180°-∠C-∠B
=180°-45°-65°=70°
∵AE是∠BAC的角平分线,
∴∠BAE=
又∵在△ABC中,∠DAB=180°-∠ADB-∠B
=180°-90°-65°=25°
∴∠DAE=∠BAE-∠DAB=35°-25°=10°
例4、
如图1所示,点P是△ABC内一点,试说明∠A与
∠P的大小关系。
图1
图 2
解: 延长BP交AC于点E,如图2所示
∵∠BPC是△PEC的一个外角
∴∠BPC>∠PEC 又∵∠PEC是△ABE的一个外角
∴∠PEC>∠A
∴∠BPC>∠A,即∠P>∠A
1.判断∠1与∠3的大小,并说明理由。
解:∠3 > ∠1
∵∠3 >∠2 ,∠2 >∠1
∴∠3 >∠1
2、如图:∠1=25°,
∠2=95°,∠3=30°,
则∠4=_______
A
D
E
C
B
1
4
3
2
30°
练一练
F
例5、
如图所示,在△ABC中,∠B=36°,∠ACB=110°,AE是
∠BAC的平分线,AD是BC边上的高,求∠DAE的大小。
解: ∵∠ACB+∠B+∠BAC=180°
∴∠BAC=180°-∠ACB-∠B
=180°-110°-36°=34°
∵AE平分∠BAC
∴
∵∠ACB=∠CAD+∠D ∴∠CAD=∠ACB-∠D
∵AD是BC边上的高 ∴∠D=90°
∴∠CAD=∠ACB-∠D=110°-90°=20°
∴∠DAE=∠EAC+∠CAD=17°+20°=37°
再 见
