随机事件及其概率
图片预览






文档简介
(共16张PPT)
随机事件及其概率
在第二次世界大战中,美国曾经宣布:一名优秀数学家的作用超过10个师的兵力.这句话有一个非同寻常的来历.
1943年以前,在大西洋上英美运输船队常常受到德国潜艇的袭击,当时,英美两国限于实力,无力增派更多的护航舰,一时间,德军的“潜艇战”搞得盟军焦头烂额.
为此,有位美国海军将领专门去请教了几位数学家,数学家们运用概率论分析后分析,舰队与敌潜艇相遇是一个随机事件,从数学角度来看这一问题,它具有一定的规律性.一定数量的船(为100艘)编队规模越小,编次就越多(为每次20艘,就要有5个编次),编次越多,与敌人相遇的概率就越大.
美国海军接受了数学家的建议,命令舰队在指定海域集合,再集体通过危险海域,然后各自驶向预定港口.结果奇迹发生了:盟军舰队遭袭被击沉的概率由原来的25%降为1%,大大减少了损失,保证了物资的及时供应.
1名数学家=10个师
考虑下列现象发生的可能性:
汽车排放尾气,污染环境;
实心铁块丢入水中,铁块浮起;
买一张彩票,中奖;
实数a,b都不为0,但 ;
明天早晨有雾;
掷一枚硬币,正面向上.
随机事件及其概率
在一定条件下, 必然会发生的事件叫做必然事件(certain event).
在一定条件下,肯定不会发生的事件叫做不可能事件(impossible event).
在一定条件下, 可能发生也可能不发生的事件叫做随机事件(random event).
投币实验:抛掷一枚硬币,观察它落地时哪一面朝上
你的结果和其他同学一致吗?为什么会出现这样的情况?
重复进行试验并记录结果,各小组的结果(正面朝上的次数)一致吗?
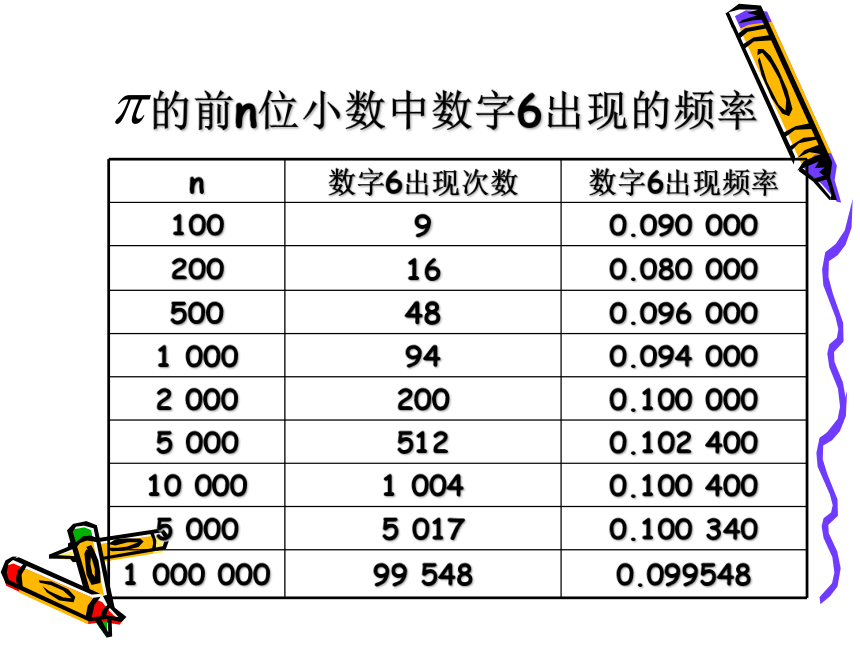
的前n位小数中数字6出现的频率
n 数字6出现次数 数字6出现频率
100 9 0.090 000
200 16 0.080 000
500 48 0.096 000
1 000 94 0.094 000
2 000 200 0.100 000
5 000 512 0.102 400
10 000 1 004 0.100 400
5 000 5 017 0.100 340
1 000 000 99 548 0.099548
随机事件A的概率
一般地,如果随机事件A在n
次试验中发生了m次,当试验的次
数n很大时,我们可以将事件A发生
的频率 作为事件A的概率的近似值,即
P(A) .
(1)频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率,并在其附近摆动.
(2)频率本身是随机的,在试验前不能确定.
(3)概率是一个确定的数,是客观存在的,与试验无关.
概率与频率
求一个事件的概率的基本方法是通过大量的重复试验;
只有当频率在某个常数附近摆动时,这个常数才叫做事件A的概率;
概率是频率的稳定值,而频率是概率的近似值;
概率反映了随机事件发生的可能性大小;
必然事件的概率为1,不可能事件的概率是0.即随机事件的概率是0≤P(A)≤1.
概率的求法与范围
例: 对某电视机厂生产的电视机进行抽样检测的数据如下:
抽取台数(n) 50 100 200 300 500 1000
优等品数(m) 40 92 192 285 478 954
优等品频率
(m/n)
(1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率约是多少(精确到0.01)?
0.8
0.92
0.96
0.95
0.956
0.954
练习:1、下列说法是否正确,
(1)中奖率为1/1000的彩票,买1000张一定中奖.
(3)某医院治疗一种疾病的治愈率为10%,那么,前9个病人都没有治愈,第10个人就一定能治愈.
(2)掷一枚硬币,连续出现5次正面向上,我认为下次出现反面向上的概率大于0.5.
2、给出一个概率很小的随机事件的例子.
给出一个概率很大的随机事件的例子.
3、统计姚明参加NBA以来的罚球命中率.
以下是新浪网对姚明参加NBA以来罚球数据的统计:
赛 季 02-03 03-04 04-05 季后赛 全明星
命中个数 301 361 389 53 1
投篮个数 371 446 497 72 2
命中频率
请根据上述数据,指出姚明在NBA比赛中罚球命中的概率.
0.81
0.81
0.78
0.74
0.5
1、随机事件发生的不确定性及频率的稳定性. (对立统一)
3、概率的范围:0≤P(A)≤1.
2、随机事件的概率的统计定义:
随机事件在相同的条件下进行大量的试验时,呈现规律性,且频率 总是接近于常数P(A),称P(A)为事件的概率.
回顾小结:
1.课后实验:全班同学每人抛掷一次性纸杯20次,先分别统计杯口朝下的频数和频率,再分组统计杯口朝下的频数和频率,最后对全班统计杯口朝下的频数和频率,由此对杯口朝下的概率作出估计.
2. 课后阅读:课本P.91的例2
谢谢合作!
随机事件及其概率
在第二次世界大战中,美国曾经宣布:一名优秀数学家的作用超过10个师的兵力.这句话有一个非同寻常的来历.
1943年以前,在大西洋上英美运输船队常常受到德国潜艇的袭击,当时,英美两国限于实力,无力增派更多的护航舰,一时间,德军的“潜艇战”搞得盟军焦头烂额.
为此,有位美国海军将领专门去请教了几位数学家,数学家们运用概率论分析后分析,舰队与敌潜艇相遇是一个随机事件,从数学角度来看这一问题,它具有一定的规律性.一定数量的船(为100艘)编队规模越小,编次就越多(为每次20艘,就要有5个编次),编次越多,与敌人相遇的概率就越大.
美国海军接受了数学家的建议,命令舰队在指定海域集合,再集体通过危险海域,然后各自驶向预定港口.结果奇迹发生了:盟军舰队遭袭被击沉的概率由原来的25%降为1%,大大减少了损失,保证了物资的及时供应.
1名数学家=10个师
考虑下列现象发生的可能性:
汽车排放尾气,污染环境;
实心铁块丢入水中,铁块浮起;
买一张彩票,中奖;
实数a,b都不为0,但 ;
明天早晨有雾;
掷一枚硬币,正面向上.
随机事件及其概率
在一定条件下, 必然会发生的事件叫做必然事件(certain event).
在一定条件下,肯定不会发生的事件叫做不可能事件(impossible event).
在一定条件下, 可能发生也可能不发生的事件叫做随机事件(random event).
投币实验:抛掷一枚硬币,观察它落地时哪一面朝上
你的结果和其他同学一致吗?为什么会出现这样的情况?
重复进行试验并记录结果,各小组的结果(正面朝上的次数)一致吗?
的前n位小数中数字6出现的频率
n 数字6出现次数 数字6出现频率
100 9 0.090 000
200 16 0.080 000
500 48 0.096 000
1 000 94 0.094 000
2 000 200 0.100 000
5 000 512 0.102 400
10 000 1 004 0.100 400
5 000 5 017 0.100 340
1 000 000 99 548 0.099548
随机事件A的概率
一般地,如果随机事件A在n
次试验中发生了m次,当试验的次
数n很大时,我们可以将事件A发生
的频率 作为事件A的概率的近似值,即
P(A) .
(1)频率是概率的近似值,随着试验次数的增加,频率会越来越接近概率,并在其附近摆动.
(2)频率本身是随机的,在试验前不能确定.
(3)概率是一个确定的数,是客观存在的,与试验无关.
概率与频率
求一个事件的概率的基本方法是通过大量的重复试验;
只有当频率在某个常数附近摆动时,这个常数才叫做事件A的概率;
概率是频率的稳定值,而频率是概率的近似值;
概率反映了随机事件发生的可能性大小;
必然事件的概率为1,不可能事件的概率是0.即随机事件的概率是0≤P(A)≤1.
概率的求法与范围
例: 对某电视机厂生产的电视机进行抽样检测的数据如下:
抽取台数(n) 50 100 200 300 500 1000
优等品数(m) 40 92 192 285 478 954
优等品频率
(m/n)
(1)计算表中优等品的各个频率;
(2)该厂生产的电视机优等品的概率约是多少(精确到0.01)?
0.8
0.92
0.96
0.95
0.956
0.954
练习:1、下列说法是否正确,
(1)中奖率为1/1000的彩票,买1000张一定中奖.
(3)某医院治疗一种疾病的治愈率为10%,那么,前9个病人都没有治愈,第10个人就一定能治愈.
(2)掷一枚硬币,连续出现5次正面向上,我认为下次出现反面向上的概率大于0.5.
2、给出一个概率很小的随机事件的例子.
给出一个概率很大的随机事件的例子.
3、统计姚明参加NBA以来的罚球命中率.
以下是新浪网对姚明参加NBA以来罚球数据的统计:
赛 季 02-03 03-04 04-05 季后赛 全明星
命中个数 301 361 389 53 1
投篮个数 371 446 497 72 2
命中频率
请根据上述数据,指出姚明在NBA比赛中罚球命中的概率.
0.81
0.81
0.78
0.74
0.5
1、随机事件发生的不确定性及频率的稳定性. (对立统一)
3、概率的范围:0≤P(A)≤1.
2、随机事件的概率的统计定义:
随机事件在相同的条件下进行大量的试验时,呈现规律性,且频率 总是接近于常数P(A),称P(A)为事件的概率.
回顾小结:
1.课后实验:全班同学每人抛掷一次性纸杯20次,先分别统计杯口朝下的频数和频率,再分组统计杯口朝下的频数和频率,最后对全班统计杯口朝下的频数和频率,由此对杯口朝下的概率作出估计.
2. 课后阅读:课本P.91的例2
谢谢合作!
