11.1.2 三角形的高、中线与角平分线课件(共22张PPT)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 10:53:08 | ||
图片预览





文档简介
11.1.2 三角形的高、中线
与角平分线
第十一章 三角形
2021-2022学年初中数学人教版八年级上册
1、认识三角形的高、中线、角平分线;
2、会画出任意三角形的高、 中线、角平分线;
3、通过画图、折纸了解三角形的三条高、
三条中线、三条角平分线交于一点.
学习目标
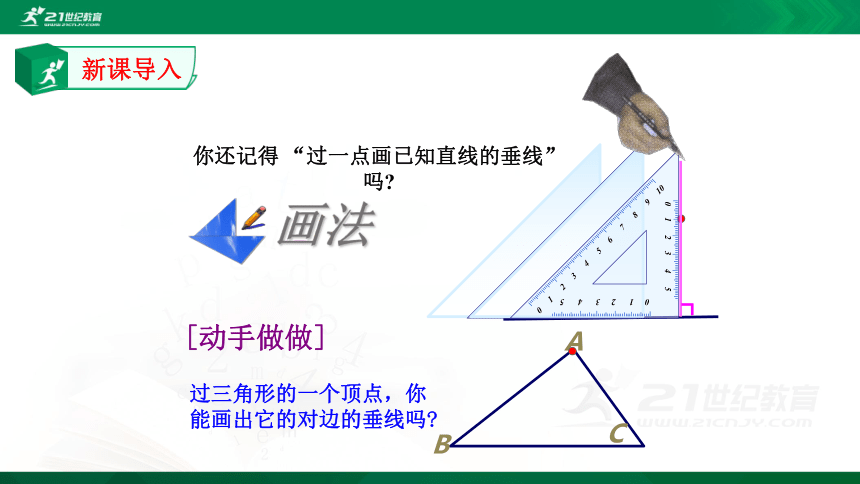
你还记得 “过一点画已知直线的垂线” 吗?
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
过三角形的一个顶点,你能画出它的对边的垂线吗?
B
C
[动手做做]
┓
新课导入
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边的高,
简称三角形的高.
如图,线段AD是BC边上的高.
三角形高的符号语言:
∵AD是△ABC的高,
∴∠BDA=∠CDA=90°.
探究新知
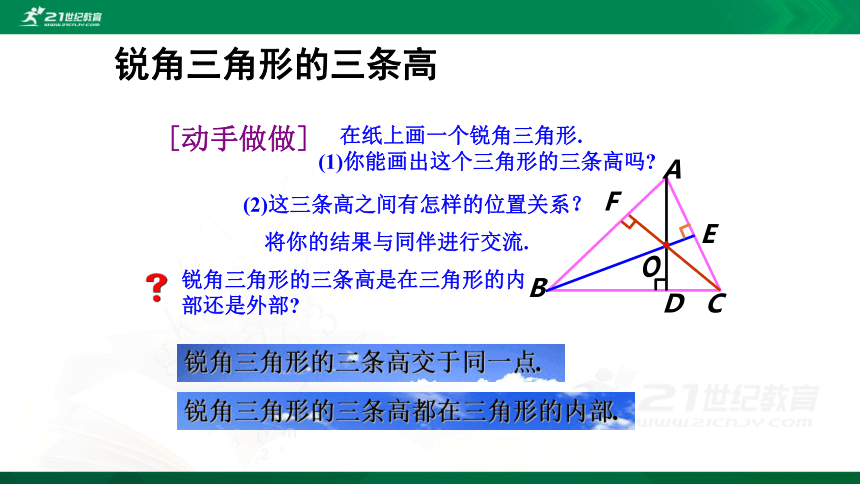
锐角三角形的三条高
在纸上画一个锐角三角形.
(1)你能画出这个三角形的三条高吗?
(2)这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
O
锐角三角形的三条高是在三角形的内部还是外部?
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
[动手做做]
直角三角形的三条高
在纸上画一个直角三角形.
将你的结果与同伴进行交流.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是 .
BD
●
[动手做做]
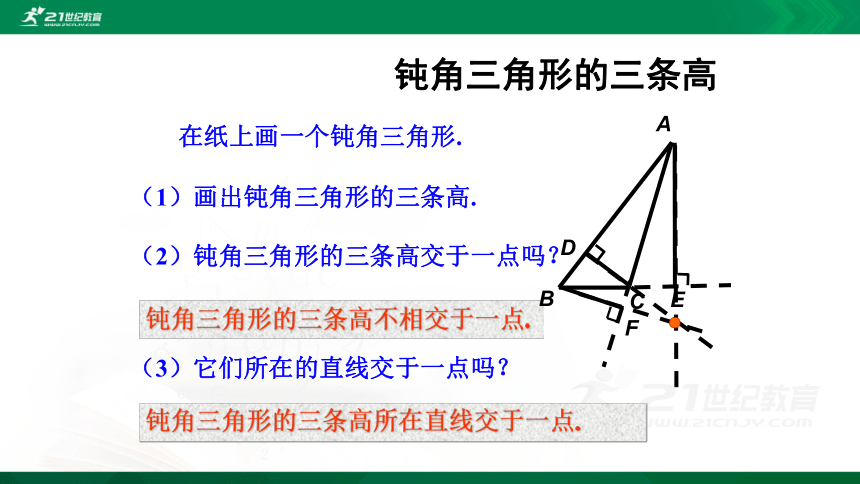
钝角三角形的三条高
在纸上画一个钝角三角形.
(1)画出钝角三角形的三条高.
F
E
(2)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点.
(3)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点.
A
B
C
D
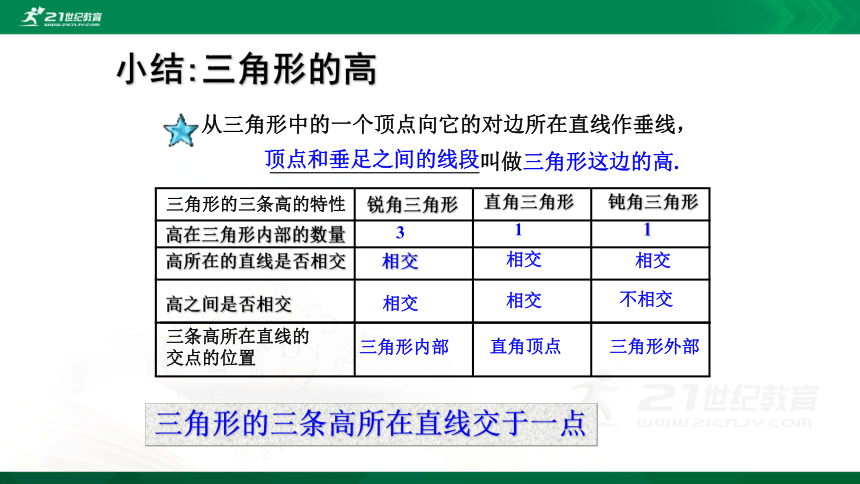
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高.
三角形的三条高的特性
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
三角形的中线
在三角形中,连结一个顶点和它对边中点的线段
叫做这个三角形这边的中线.
A
B
C
D
∵AD是△ABC的中线,
∴BD=CD =
1
2
BC.
任意画一个三角形,然后画出这个三角形三
条边的中线,你发现了什么?
●
●
三角形的三条中线相交于一点,交点在三角形的内部.
三角形中线的符号语言:
E
F
O
[动手做做]
三角形的中线
A
B
C
D
●
●
E
F
O
三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
如图,△ABC的重心是点O.
三角形的角平分线
∵AD是 △ ABC的角平分线,
∴∠BAD = ∠CAD =
1
2
∠BAC.
任意画一个三角形,然后画出这个三角形
三个角的角平分线,你发现了什么?
三角形的三条角平分线相交于一点,
交点在三角形的内部.
在三角形中,一个内角的角平分线与它的对边相交,这个
角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
︶
︶
1
2
[动手做做]
A
C
B
F
E
D
O
∵BE是△ABC的角平分线,
∴ = _____ = _____.
∴∠ACB=2______=2______.
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线,
∠BCF
角平分线的符号语言
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线.
如图,在△ABC中, ∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD于点H,判断下列说法那些是正确的,哪些是错误的?
①AD是△ABE的角平分线 ( )
②BE是△ABD边AD上的中线( )
③BE是△ABC边AC上的中线( )
④CH是△ACD边AD上的高 ( )
三角形的高、中线与角平分线都是线段.
×
×
×
√
⌒
⌒
A
B
C
D
E
1
2
F
G
H
┓
针对练习
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,
那么这个三角形是( )
A.等边三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1.下列各组图形中,哪一组中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
课堂练习
AF
CD
AC
3.填空:
(1)如图1,AD,BE,CF是△ABC的三条中线,
则AB=2 ,BD= ,AE = .
(2)如图2, AD,BE,CF是△ ABC的三条角平分线,
则∠1= , ∠3= , ∠ACB= 2 .
∠2
∠ABC
∠4
图1
F
E
D
C
B
A
图2
F
E
D
C
B
A
4
3
2
1
4.填空:如图,在△ ABC中,AE是中 线,AD是角平分线,AF是高.
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°.
CE
BC
∠CAD
∠BAC
∠AFC
F
E
D
C
B
A
5.如图所示,在△ABC中,∠ACB=90°,把△ABC 沿直线AC 翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D
B
'
C
B
A
6.如图所示,D,E分别是△ABC 的边AC,BC 的中点,则下列说法不正确的是( )
A.DE是△BCD 的中线 B.BD是△ABC 的中线
C.AD=DC,BD=EC D.∠C 的对边是DE
C
E
D
C
B
A
1.三角形的高、中线、角平分线的有关概念及它们的画法.
2.三角形的高、中线、角平分线的符号语言及简单应用.
通过本课时的学习,我们学习了
小 结
课堂小结
谢谢聆听
与角平分线
第十一章 三角形
2021-2022学年初中数学人教版八年级上册
1、认识三角形的高、中线、角平分线;
2、会画出任意三角形的高、 中线、角平分线;
3、通过画图、折纸了解三角形的三条高、
三条中线、三条角平分线交于一点.
学习目标
你还记得 “过一点画已知直线的垂线” 吗?
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
画法
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
0 1 2 3 4 5 6 7 8 9 10
0 1 2 3 4 5
0 1 2 3 4 5
A
过三角形的一个顶点,你能画出它的对边的垂线吗?
B
C
[动手做做]
┓
新课导入
A
从三角形的一个顶点
B
C
向它的对边
所在直线作垂线,
顶点
和垂足
D
之间的线段
叫做三角形这边的高,
简称三角形的高.
如图,线段AD是BC边上的高.
三角形高的符号语言:
∵AD是△ABC的高,
∴∠BDA=∠CDA=90°.
探究新知
锐角三角形的三条高
在纸上画一个锐角三角形.
(1)你能画出这个三角形的三条高吗?
(2)这三条高之间有怎样的位置关系?
将你的结果与同伴进行交流.
O
锐角三角形的三条高是在三角形的内部还是外部?
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
[动手做做]
直角三角形的三条高
在纸上画一个直角三角形.
将你的结果与同伴进行交流.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是 ;
AB
直角边AB边上的高是 ;
CB
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
D
斜边AC边上的高是 .
BD
●
[动手做做]
钝角三角形的三条高
在纸上画一个钝角三角形.
(1)画出钝角三角形的三条高.
F
E
(2)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点.
(3)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点.
A
B
C
D
小结:三角形的高
从三角形中的一个顶点向它的对边所在直线作垂线,
顶点和垂足之间的线段
叫做三角形这边的高.
三角形的三条高的特性
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三角形的三条高所在直线交于一点
三条高所在直线的
交点的位置
三角形内部
直角顶点
三角形外部
三角形的中线
在三角形中,连结一个顶点和它对边中点的线段
叫做这个三角形这边的中线.
A
B
C
D
∵AD是△ABC的中线,
∴BD=CD =
1
2
BC.
任意画一个三角形,然后画出这个三角形三
条边的中线,你发现了什么?
●
●
三角形的三条中线相交于一点,交点在三角形的内部.
三角形中线的符号语言:
E
F
O
[动手做做]
三角形的中线
A
B
C
D
●
●
E
F
O
三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
如图,△ABC的重心是点O.
三角形的角平分线
∵AD是 △ ABC的角平分线,
∴∠BAD = ∠CAD =
1
2
∠BAC.
任意画一个三角形,然后画出这个三角形
三个角的角平分线,你发现了什么?
三角形的三条角平分线相交于一点,
交点在三角形的内部.
在三角形中,一个内角的角平分线与它的对边相交,这个
角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
︶
︶
1
2
[动手做做]
A
C
B
F
E
D
O
∵BE是△ABC的角平分线,
∴ = _____ = _____.
∴∠ACB=2______=2______.
∠ABE
∠CBE
∠ABC
∠ACF
∵CF是△ABC的角平分线,
∠BCF
角平分线的符号语言
三角形的角平分线与角的平分线有什么区别?
思考
三角形的角平分线是一条线段 , 角的平分线是一条射线.
如图,在△ABC中, ∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD于点H,判断下列说法那些是正确的,哪些是错误的?
①AD是△ABE的角平分线 ( )
②BE是△ABD边AD上的中线( )
③BE是△ABC边AC上的中线( )
④CH是△ACD边AD上的高 ( )
三角形的高、中线与角平分线都是线段.
×
×
×
√
⌒
⌒
A
B
C
D
E
1
2
F
G
H
┓
针对练习
2.如果一个三角形的三条高的交点恰是三角形的一个顶点,
那么这个三角形是( )
A.等边三角形 B.直角三角形
C.钝角三角形 D.锐角三角形
1.下列各组图形中,哪一组中AD是△ABC 的高( )
A
D
C
B
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
B
D
课堂练习
AF
CD
AC
3.填空:
(1)如图1,AD,BE,CF是△ABC的三条中线,
则AB=2 ,BD= ,AE = .
(2)如图2, AD,BE,CF是△ ABC的三条角平分线,
则∠1= , ∠3= , ∠ACB= 2 .
∠2
∠ABC
∠4
图1
F
E
D
C
B
A
图2
F
E
D
C
B
A
4
3
2
1
4.填空:如图,在△ ABC中,AE是中 线,AD是角平分线,AF是高.
(1)BE= = ;
(2)∠BAD= = ;
(3)∠AFB= = 90°.
CE
BC
∠CAD
∠BAC
∠AFC
F
E
D
C
B
A
5.如图所示,在△ABC中,∠ACB=90°,把△ABC 沿直线AC 翻折180°,使点B 落在点B′的位置,则线段AC具有性质( )
A.是边BB′上的中线 B.是边BB′上的高
C.是∠BAB′的角平分线 D.以上三种性质合一
D
B
'
C
B
A
6.如图所示,D,E分别是△ABC 的边AC,BC 的中点,则下列说法不正确的是( )
A.DE是△BCD 的中线 B.BD是△ABC 的中线
C.AD=DC,BD=EC D.∠C 的对边是DE
C
E
D
C
B
A
1.三角形的高、中线、角平分线的有关概念及它们的画法.
2.三角形的高、中线、角平分线的符号语言及简单应用.
通过本课时的学习,我们学习了
小 结
课堂小结
谢谢聆听
