一次函数
图片预览




文档简介
(共13张PPT)
课前热身
(1) 是一次函数的有
(2)是正比例函数的有
3.一次函数y=3x-2中,y随x的增大而 ,
图像经过第 象限。
ACDG
D G
增大
一、二、四
2.一次函数y=3x+6的图像与x轴的交点是
与y轴的交点是
(-2,0)
(0,6)
一次函数的图象
一次函数 的图象是经过点
的一条直线.
正比例函数 的图象是经过原
点(0,0)的一条直线.
画一次函数的图象,只要先描出两点,
再连成直线.
考点聚焦2
考点聚焦1
一次函数的解析式为:
正比例函数的解析式为:
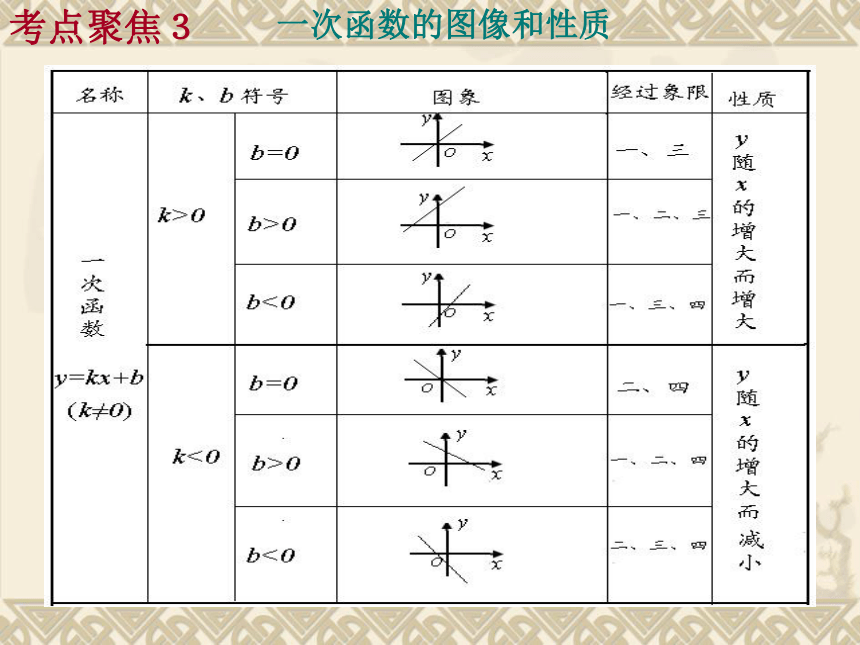
考点聚焦3
一次函数的图像和性质
(一)、填空题:
1.当m 时,y=x+m-2 是正比例函数;
当m 时, 是一次函数.
2.一次函数y=3x+b的图像经过坐标原点,则b的值为
3.一次函数 y= (a-1)x+b+1中,y随x的增大而减小,图像经过第一、二、四象限,
则a , b
=2
=-1
0
<1
>-1
x
0 1 2 3 4 5 6
1
2
3
4
y
-1
-2
A(2,4)
B
O
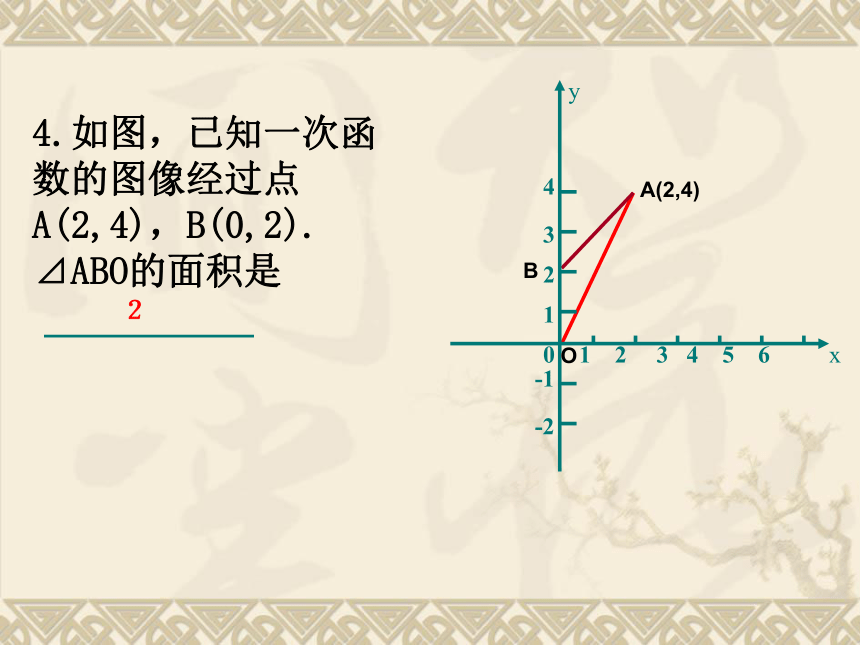
4.如图,已知一次函数的图像经过点A(2,4),B(0,2).
⊿ABO的面积是
2
(二)、选择题:
1.一次函数 y= kx-2, y随x的增大而减小,则它的图像一定不经过( )
A 第一 象限 B 第 二 象限
C 第三象限 D 第 四象限
2.已知一次函数 y= (a-1)x+b的图像如右图所示,那么( )
A . a>0,b>0 B. a<0, b<0
C. a>1,b>0 D. a<1,b=0
y
x
O
3.下列各点中,在函数y=2x-7的图像
上的是( )
A. (2,3) B.(3,1) C.(0,-7) D.(-1,9)
A
C
C
(三)图像信息题
已知一次函数的图象如图所示:
(1)此一次函数的解析式为:
(2)观察图象,当x 时,y> 0; 当x 时,y=0;当x 时,y<0;
(3)观察图象,当x=2时,y= ,
当y=1时x= ;
(4)不解方程,求
x+2=0的解;
(5)不解不等式,求 x+2<0的解。
x
y
o
1
2
3
-1
-2
-3
1
2
3
-4
-1
-2
-3
>-4
=-4
<-4
3
-2
y= x+2
x=-4
x<-4
(四)解答题
某商店购进一种家电产品,如果每天卖出12件,则25天可以全部售完。
(1)试为这种家电产品的存货量与售出时间的关系建立一个函数模型。
(2)售出10天后,这种家电产品还有多少?
解:(1)由题意可知这种家电产品的存货量为:
12×25=300(件)
设存货量y件,售出时间x天,则y与x的函数关系为:y=300-12x (0≤x≤25)
(2) 当x=10时,y=300-12×10=180(件)
答:售出10天后,这种家电产品还有180件。
一次函数
函数 正比例函数
y=kx(k≠0) 一次函数
y=kx+b( k≠0)
图象
性质
过(0,b), (- ,0)两点的直线
过(0,0), (1,k)两点的直线
k>0
k<0
y随x的增大而增大
y随x的增大而减小
布置作业
1、一次函数y=(m+2)x-3的图像经过坐标平面内的第一、三、四象限,那么=m
2、已知一次函数的图像经过点(0,3)与(2,1),则这个一次函数中随的增大而
3、已知一次函数的图像经过A(2,-1),B(-1,2)两点,求这个函数的解析式。
课前热身
(1) 是一次函数的有
(2)是正比例函数的有
3.一次函数y=3x-2中,y随x的增大而 ,
图像经过第 象限。
ACDG
D G
增大
一、二、四
2.一次函数y=3x+6的图像与x轴的交点是
与y轴的交点是
(-2,0)
(0,6)
一次函数的图象
一次函数 的图象是经过点
的一条直线.
正比例函数 的图象是经过原
点(0,0)的一条直线.
画一次函数的图象,只要先描出两点,
再连成直线.
考点聚焦2
考点聚焦1
一次函数的解析式为:
正比例函数的解析式为:
考点聚焦3
一次函数的图像和性质
(一)、填空题:
1.当m 时,y=x+m-2 是正比例函数;
当m 时, 是一次函数.
2.一次函数y=3x+b的图像经过坐标原点,则b的值为
3.一次函数 y= (a-1)x+b+1中,y随x的增大而减小,图像经过第一、二、四象限,
则a , b
=2
=-1
0
<1
>-1
x
0 1 2 3 4 5 6
1
2
3
4
y
-1
-2
A(2,4)
B
O
4.如图,已知一次函数的图像经过点A(2,4),B(0,2).
⊿ABO的面积是
2
(二)、选择题:
1.一次函数 y= kx-2, y随x的增大而减小,则它的图像一定不经过( )
A 第一 象限 B 第 二 象限
C 第三象限 D 第 四象限
2.已知一次函数 y= (a-1)x+b的图像如右图所示,那么( )
A . a>0,b>0 B. a<0, b<0
C. a>1,b>0 D. a<1,b=0
y
x
O
3.下列各点中,在函数y=2x-7的图像
上的是( )
A. (2,3) B.(3,1) C.(0,-7) D.(-1,9)
A
C
C
(三)图像信息题
已知一次函数的图象如图所示:
(1)此一次函数的解析式为:
(2)观察图象,当x 时,y> 0; 当x 时,y=0;当x 时,y<0;
(3)观察图象,当x=2时,y= ,
当y=1时x= ;
(4)不解方程,求
x+2=0的解;
(5)不解不等式,求 x+2<0的解。
x
y
o
1
2
3
-1
-2
-3
1
2
3
-4
-1
-2
-3
>-4
=-4
<-4
3
-2
y= x+2
x=-4
x<-4
(四)解答题
某商店购进一种家电产品,如果每天卖出12件,则25天可以全部售完。
(1)试为这种家电产品的存货量与售出时间的关系建立一个函数模型。
(2)售出10天后,这种家电产品还有多少?
解:(1)由题意可知这种家电产品的存货量为:
12×25=300(件)
设存货量y件,售出时间x天,则y与x的函数关系为:y=300-12x (0≤x≤25)
(2) 当x=10时,y=300-12×10=180(件)
答:售出10天后,这种家电产品还有180件。
一次函数
函数 正比例函数
y=kx(k≠0) 一次函数
y=kx+b( k≠0)
图象
性质
过(0,b), (- ,0)两点的直线
过(0,0), (1,k)两点的直线
k>0
k<0
y随x的增大而增大
y随x的增大而减小
布置作业
1、一次函数y=(m+2)x-3的图像经过坐标平面内的第一、三、四象限,那么=m
2、已知一次函数的图像经过点(0,3)与(2,1),则这个一次函数中随的增大而
3、已知一次函数的图像经过A(2,-1),B(-1,2)两点,求这个函数的解析式。
