3.4.4 实际问题与一元一次方程 课件(共21张PPT)
文档属性
| 名称 | 3.4.4 实际问题与一元一次方程 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 15:31:45 | ||
图片预览





文档简介
第三章 一元一次方程
3.4实际问题与一元一次方程
第四课时 电话计费问题
2021-2022学年初中数学人教版七年级上册
1.通过对这种电话计费问题的探究学习,掌握分段计算的技巧.
2.通过探究实际问题与一元一次方程的关系,感受数学的应用价值,提高分析问题、解决问题的能力.
3.把生活中的实际问题抽象成数学问题.
学习目标
在科技迅猛发展的今天,移动电话成为了人们生活中非常普及的通讯工具,选择经济实惠的资费方式成为了我们所关心而且具有实际意义的问题,你知道你的家人都选择了哪种资费吗?
新课导入
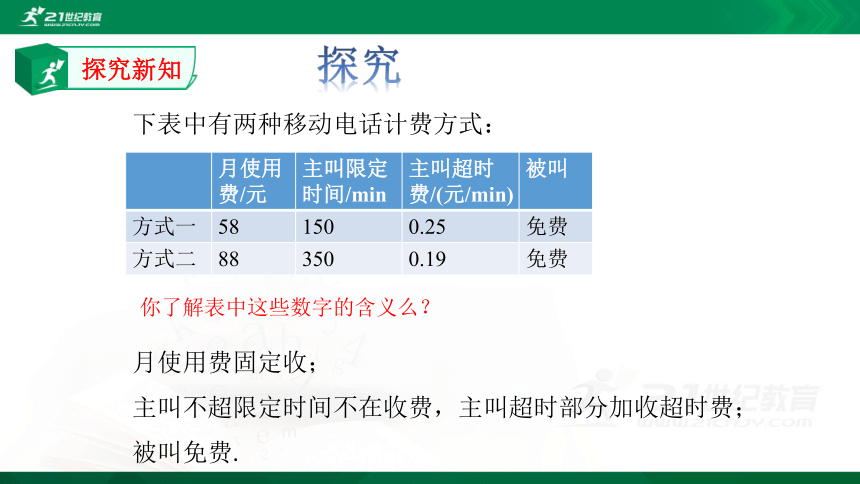
下表中有两种移动电话计费方式:
探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
你了解表中这些数字的含义么?
月使用费固定收;
主叫不超限定时间不在收费,主叫超时部分加收超时费;
被叫免费.
探究新知
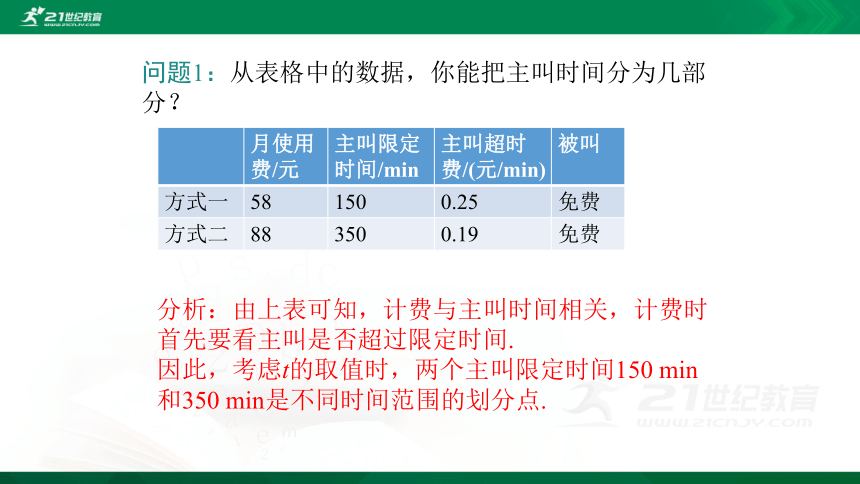
问题1:从表格中的数据,你能把主叫时间分为几部分?
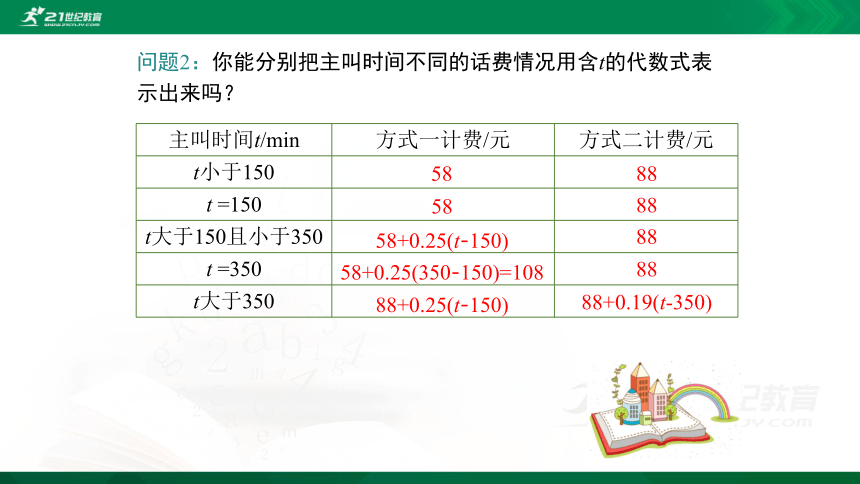
问题2:你能分别把主叫时间不同的话费情况用含t的代数式表示出来吗?
问题3:(1)在两种收费方式下,会不会有这么一个时间,打不同样多时间的电话,却收费相同呢?
(2)如果有这一时间,那么如何分别表示收费表达式呢?(“收费相等”是本题列方程的等量关系)
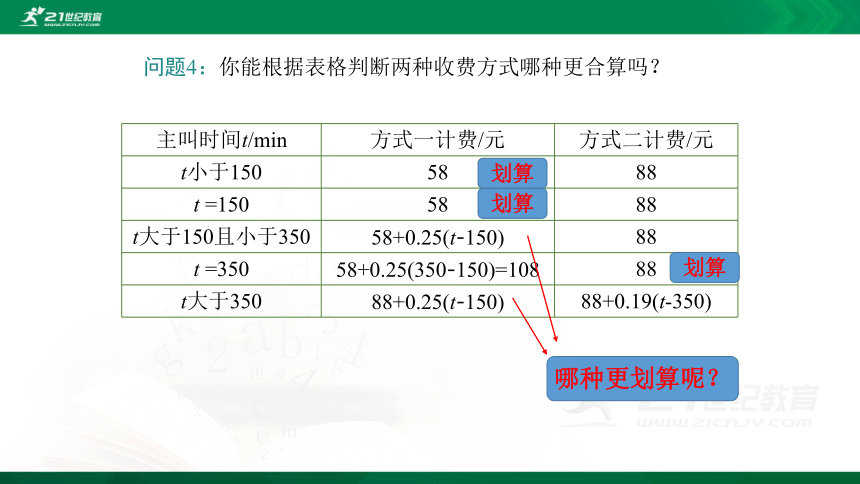
问题4:你能根据表格判断两种收费方式哪种更合算吗?
分析:由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间.
因此,考虑t的取值时,两个主叫限定时间150 min和350 min是不同时间范围的划分点.
问题1:从表格中的数据,你能把主叫时间分为几部分?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
问题2:你能分别把主叫时间不同的话费情况用含t的代数式表示出来吗?
{5940675A-B579-460E-94D1-54222C63F5DA}主叫时间t/min
方式一计费/元
方式二计费/元
t小于150
t =150
t大于150且小于350
t =350
t大于350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
88+0.25(t-150)
88
88
88
88
88+0.19(t-350)
问题3:(1)在两种收费方式下,会不会有这么一个时间,打不同样多时间的电话,却收费相同呢?
问题3: (2)如果有这一时间,那么如何分别表示收费表达式呢?(“收费相等”是本题列方程的等量关系)
会,在t大于150且小于350时
{5940675A-B579-460E-94D1-54222C63F5DA}t大于150且小于350
58+0.25(350-150)=108
88
依题意得:58+0.25(t-150)=88
解得:t=270
所以当 t =270分时,两种计费方式的费用相等
问题4:你能根据表格判断两种收费方式哪种更合算吗?
{5940675A-B579-460E-94D1-54222C63F5DA}主叫时间t/min
方式一计费/元
方式二计费/元
t小于150
58
88
t =150
58
88
t大于150且小于350
58+0.25(t-150)
88
t =350
58+0.25(350-150)=108
88
t大于350
88+0.25(t-150)
88+0.19(t-350)
划算
划算
划算
哪种更划算呢?
综合以上的分析,可以发现:
当t大于350时,按方式一的计费58+0.25(t-150)可变形为108+0.25(t-350).对比按方式二的计费,你能说明此时按哪种方式的计费少吗?
______________时,选择方式一省钱;
______________时,选择方式二省钱;
______________时,方式一、方式二均可.
t小于270
t大于270
t等于270
课后问题:当t大于350时,按方式一的计费58+0.25(t-150)可变形为108+0.25(t-350).对比按方式二的计费,你能说明此时按哪种方式的计费少吗?
1.某商场销售一种西装和领带,西装每套定价1000元,领带每条定价200元.“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
课堂练习
(1)若该客户按方案一购买,需付款________元.若该客户按方案二购买,需付款________;(用含x的代数式表示)
解析:(1)根据题目提供的两种不同的付款方式列出代数式即可;
解:(1)客户要到该商场购买西装20套,领带x条(x>20).
方案一费用:200x+16000,
方案二费用:180x+18000;
课堂练习
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
解析:(2)将x=30代入求得的代数式中即可得到费用,然后比较即可得到选择哪种方案更合算;
解:(2)当x=30时,方案一:200×30+16000=22000(元),
方案二:180×30+18000=23400(元),
所以,按方案一购买较合算.
课堂练习
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
解析:(3)根据题意可以得到先按方案一购买20套西装获赠送20条领带,再按方案二购买10条领带更合算.
解:(3)先按方案一购买20套西装获赠送20条领带,再按方案二购买10条领带.
则20000+200×10×90%=21800(元).
课堂练习
2.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}档次
每户每月用电数(度)
执行电价(元/度)
第一档
小于等于200
0.55
第二档
大于200小于400
0.6
第三档
大于等于400
0.85
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).
课堂练习
某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?
解析:某户居民五、六月份共用电500度,就可以得出每月用电量不可能都在第一档,分情况讨论,当5月份用电量为x度≤200度,6月份用电(500-x)度,当5月份用电量为x度>200度,六月份用电量为(500-x)度,分别建立方程求出其解即可.
解:当5月份用电量为x度≤200度,6月份用电(500-x)度,由题意得
0.55x+0.6×(500-x)=290.5,
解得x=190,
∴6月份用电500-x=310(度).
当5月份用电量为x度>200度,六月份用电量为(500-x)度>200度,由题意得
0.6x+0.6×(500-x)=290.5,
方程无解,
∴该情况不符合题意.
答:该户居民五、六月份分别用电190度、310度.
——你学到了那些新知识呢?
1.解决电话计费问题需要明确“哪种计费方式更省钱”与“主叫时间”有关
2.此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
课堂小结
谢谢聆听
3.4实际问题与一元一次方程
第四课时 电话计费问题
2021-2022学年初中数学人教版七年级上册
1.通过对这种电话计费问题的探究学习,掌握分段计算的技巧.
2.通过探究实际问题与一元一次方程的关系,感受数学的应用价值,提高分析问题、解决问题的能力.
3.把生活中的实际问题抽象成数学问题.
学习目标
在科技迅猛发展的今天,移动电话成为了人们生活中非常普及的通讯工具,选择经济实惠的资费方式成为了我们所关心而且具有实际意义的问题,你知道你的家人都选择了哪种资费吗?
新课导入
下表中有两种移动电话计费方式:
探究
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
你了解表中这些数字的含义么?
月使用费固定收;
主叫不超限定时间不在收费,主叫超时部分加收超时费;
被叫免费.
探究新知
问题1:从表格中的数据,你能把主叫时间分为几部分?
问题2:你能分别把主叫时间不同的话费情况用含t的代数式表示出来吗?
问题3:(1)在两种收费方式下,会不会有这么一个时间,打不同样多时间的电话,却收费相同呢?
(2)如果有这一时间,那么如何分别表示收费表达式呢?(“收费相等”是本题列方程的等量关系)
问题4:你能根据表格判断两种收费方式哪种更合算吗?
分析:由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间.
因此,考虑t的取值时,两个主叫限定时间150 min和350 min是不同时间范围的划分点.
问题1:从表格中的数据,你能把主叫时间分为几部分?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
月使用费/元
主叫限定时间/min
主叫超时费/(元/min)
被叫
方式一
58
150
0.25
免费
方式二
88
350
0.19
免费
问题2:你能分别把主叫时间不同的话费情况用含t的代数式表示出来吗?
{5940675A-B579-460E-94D1-54222C63F5DA}主叫时间t/min
方式一计费/元
方式二计费/元
t小于150
t =150
t大于150且小于350
t =350
t大于350
58
58
58+0.25(t-150)
58+0.25(350-150)=108
88+0.25(t-150)
88
88
88
88
88+0.19(t-350)
问题3:(1)在两种收费方式下,会不会有这么一个时间,打不同样多时间的电话,却收费相同呢?
问题3: (2)如果有这一时间,那么如何分别表示收费表达式呢?(“收费相等”是本题列方程的等量关系)
会,在t大于150且小于350时
{5940675A-B579-460E-94D1-54222C63F5DA}t大于150且小于350
58+0.25(350-150)=108
88
依题意得:58+0.25(t-150)=88
解得:t=270
所以当 t =270分时,两种计费方式的费用相等
问题4:你能根据表格判断两种收费方式哪种更合算吗?
{5940675A-B579-460E-94D1-54222C63F5DA}主叫时间t/min
方式一计费/元
方式二计费/元
t小于150
58
88
t =150
58
88
t大于150且小于350
58+0.25(t-150)
88
t =350
58+0.25(350-150)=108
88
t大于350
88+0.25(t-150)
88+0.19(t-350)
划算
划算
划算
哪种更划算呢?
综合以上的分析,可以发现:
当t大于350时,按方式一的计费58+0.25(t-150)可变形为108+0.25(t-350).对比按方式二的计费,你能说明此时按哪种方式的计费少吗?
______________时,选择方式一省钱;
______________时,选择方式二省钱;
______________时,方式一、方式二均可.
t小于270
t大于270
t等于270
课后问题:当t大于350时,按方式一的计费58+0.25(t-150)可变形为108+0.25(t-350).对比按方式二的计费,你能说明此时按哪种方式的计费少吗?
1.某商场销售一种西装和领带,西装每套定价1000元,领带每条定价200元.“国庆节”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
课堂练习
(1)若该客户按方案一购买,需付款________元.若该客户按方案二购买,需付款________;(用含x的代数式表示)
解析:(1)根据题目提供的两种不同的付款方式列出代数式即可;
解:(1)客户要到该商场购买西装20套,领带x条(x>20).
方案一费用:200x+16000,
方案二费用:180x+18000;
课堂练习
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
解析:(2)将x=30代入求得的代数式中即可得到费用,然后比较即可得到选择哪种方案更合算;
解:(2)当x=30时,方案一:200×30+16000=22000(元),
方案二:180×30+18000=23400(元),
所以,按方案一购买较合算.
课堂练习
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
解析:(3)根据题意可以得到先按方案一购买20套西装获赠送20条领带,再按方案二购买10条领带更合算.
解:(3)先按方案一购买20套西装获赠送20条领带,再按方案二购买10条领带.
则20000+200×10×90%=21800(元).
课堂练习
2.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}档次
每户每月用电数(度)
执行电价(元/度)
第一档
小于等于200
0.55
第二档
大于200小于400
0.6
第三档
大于等于400
0.85
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).
课堂练习
某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?
解析:某户居民五、六月份共用电500度,就可以得出每月用电量不可能都在第一档,分情况讨论,当5月份用电量为x度≤200度,6月份用电(500-x)度,当5月份用电量为x度>200度,六月份用电量为(500-x)度,分别建立方程求出其解即可.
解:当5月份用电量为x度≤200度,6月份用电(500-x)度,由题意得
0.55x+0.6×(500-x)=290.5,
解得x=190,
∴6月份用电500-x=310(度).
当5月份用电量为x度>200度,六月份用电量为(500-x)度>200度,由题意得
0.6x+0.6×(500-x)=290.5,
方程无解,
∴该情况不符合题意.
答:该户居民五、六月份分别用电190度、310度.
——你学到了那些新知识呢?
1.解决电话计费问题需要明确“哪种计费方式更省钱”与“主叫时间”有关
2.此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
课堂小结
谢谢聆听
