七年级数学数据的收集和整理
文档属性
| 名称 | 七年级数学数据的收集和整理 |  | |
| 格式 | zip | ||
| 文件大小 | 209.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-05-01 16:59:04 | ||
图片预览


文档简介
《数据的收集和整理》单元检测题
学号________. 姓名________.
一.选择题 (每小题4分,共40分)
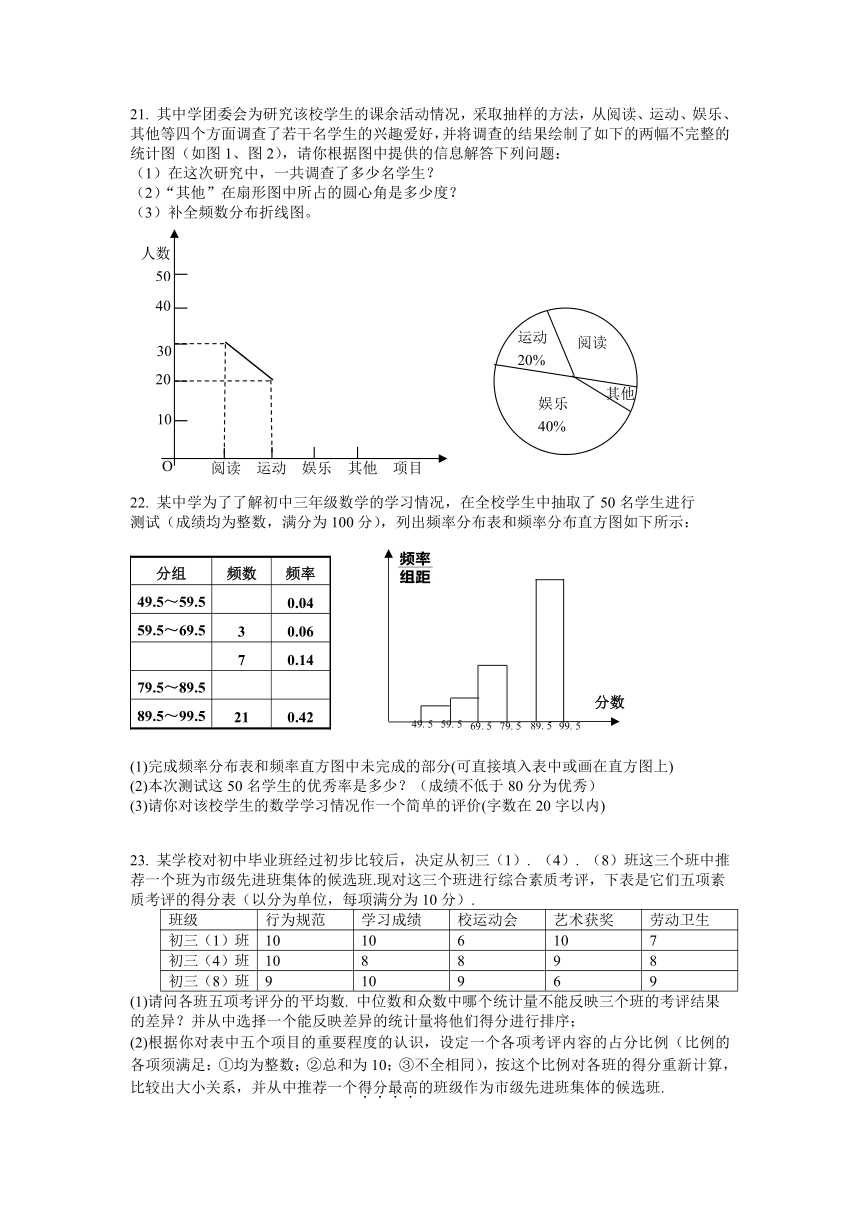
1. 超市为了制定某个时间段收银台开放方案,统计了这个
时间段本超市顾客在收银台排队付款的等待时间,并绘制成
如下的频数分布直方图(图中等待时间6分钟到7分钟表示
大于或等于6分钟而小于7分钟,其它类同).这个时间段内
顾客等待时间不少于6分钟的人数为
A.5 B.7 C.16 D.33
2. 下列调查中适合用普查方法的是
A.要了解本班同学的身高 B.要了解一批灯泡的使用寿命
C.要了解全国人口老龄化的情况 D.要了解电视台某娱乐节目的收视率
3. 右边给出的是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是
A. 69 B. 54 C. 27 D.40
4. 某青年排球队12名队员的年龄情况如下:
年龄(单位:岁) 18 19 20 21 22
人 数 1 4 3 2 2
则这个队队员年龄的众数和中位数是
A.19,20 B.19,19 C.19,20.5 D.20,19
5. 某市对2400名年满15岁的男生的身高进行了测量,结果身高(单位:m)在1.68~1.70这一小组的频率为0.25,则该组的人数为
A. 600人 B. 150 人 C.60人 D. 15人
6. “五一”黄金周期间,为了促销商品,甲、乙两个商店都采取优惠措施,甲店推出八折后再打八折,乙店则一次性六折优惠,对于同一种商品,下列结论正确的是
A.甲比乙优惠; B.乙比甲优惠;
C.两店同样优惠; D.无法比较两店的优惠程度。
7. 举世瞩目的三峡大坝于今年5月全线建成,所装发电机组全部投入运行后,预计年发电量可以达到847亿度,用科学记数法表示这个发电量为
A.847×108度 B.8.47×1010度 C.8.47×1012度 D.84.7×101010度
8. 为筹备班级的初中毕业联欢会, 班长对全班同学爱吃哪几种水果作民意调查, 从而最终决定买什么水果。下列调查数据中最值得关注的是
A. 平均数 B. 中位数 C. 众数 D. 方差
9. 如图是某地区用水量与人口数情况统计表,日平均用水量为400万吨的这一年,人口数大约是
A.180万 B.200万 C.300万 D.400万
10. 从一幅扑克牌中抽出5张红桃,4张梅花,3张黑桃放在一起洗匀后,从中一次随机抽出10张,恰好红桃.梅花.黑桃3种牌都抽到,这件事情
A.可能发生 B.不可能发生 C.很可能发生 D.必然发生
二.填空题 (每小题3分,共24分)
11. 数据22,24,21,28,37,26,30的中位数是________.
12. 一射击运动员在一次射击练习中打出的成绩是(单位:环):7,8,9,8,6,8,10,7,这组数据的众数是_________环
13. 数学老师布置10道选择题作为课堂练习,科代表将全班同学的答题情况绘制成条形统计图,根据图中信息,全班每位同学答对题数的中位数和众数分别为______________.
14. 某商场为了解本商场的服务质量,随机调查了本商场的100名顾客,调查的结果如图所示. 根据图中给出的信息,这100名顾客中对该商场的服务质量表示不满意的有 人.
15. 为了解某校九年级学生的营养状况,随机抽取了8位学生的血样进行血色素检测,以此来估计这个年级学生的平均水平,测得结果如下(单位:克):13.8,12.5,10.6,11,14.7,12.4,13.6,12.2,则这8位学生血色素的平均值为____克.
16. 为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有10条,则估计池塘里有鱼______________条.
17. 近年来,义乌市对外贸易快速增长.右图是根据我市2004年至2007年出口总额绘制的条形统计图,观察统计图可得在这期间我市年出口总额的极差是________亿美元.
18. 某校九年级三班在体育毕业考试中,全班所有学生得分的情况如下表所示:那么该班共有_________ 人,随机地抽取1人,恰好是获得30分的学生的概率是 ,从下表中,你还能获取的信息是 (写出一条即可).
分数段 18分以下 18—20分 21-23分 24-26分 27—29分 30分
人数 2 3 12 20 18 10
三.解答题 (共56分)
19. 某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售负责人把每位营销员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
20. 射击集训队在一个月集训中,对甲、乙两名运动员进行了10次测试,成绩如下:(5分)
次数 1 2 3 4 5 6 7 8 9 10
甲(环数) 9 6 6 8 7 6 6 8 8 6
乙(环数) 4 5 7 6 8 7 8 8 8 9
根据表中提供的信息,填写下表:(3分)
平均数 方差 众数
甲 7 1.2
乙 2.2
(2)如果你是教练,会选哪位运动员参加比赛,请说明理由。(3分)
21. 其中学团委会为研究该校学生的课余活动情况,采取抽样的方法,从阅读、运动、娱乐、其他等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图1、图2),请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了多少名学生?
(2)“其他”在扇形图中所占的圆心角是多少度?
(3)补全频数分布折线图。
22. 某中学为了了解初中三年级数学的学习情况,在全校学生中抽取了50名学生进行
测试(成绩均为整数,满分为100分),列出频率分布表和频率分布直方图如下所示:
(1)完成频率分布表和频率直方图中未完成的部分(可直接填入表中或画在直方图上)
(2)本次测试这50名学生的优秀率是多少?(成绩不低于80分为优秀)
(3)请你对该校学生的数学学习情况作一个简单的评价(字数在20字以内)
23. 某学校对初中毕业班经过初步比较后,决定从初三(1). (4). (8)班这三个班中推荐一个班为市级先进班集体的候选班.现对这三个班进行综合素质考评,下表是它们五项素质考评的得分表(以分为单位,每项满分为10分).
班级 行为规范 学习成绩 校运动会 艺术获奖 劳动卫生
初三(1)班 10 10 6 10 7
初三(4)班 10 8 8 9 8
初三(8)班 9 10 9 6 9
(1)请问各班五项考评分的平均数. 中位数和众数中哪个统计量不能反映三个班的考评结果的差异?并从中选择一个能反映差异的统计量将他们得分进行排序;
(2)根据你对表中五个项目的重要程度的认识,设定一个各项考评内容的占分比例(比例的各项须满足:①均为整数;②总和为10;③不全相同),按这个比例对各班的得分重新计算,比较出大小关系,并从中推荐一个得分最高的班级作为市级先进班集体的候选班.
24. 为了普及环保知识,增强环保意识,某中学组织了一次环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这此选手的决赛成绩(满分100分)如下表:
决赛成绩(单位:分)
初一级 80 86 88 80 99 80 74 91 89
初二级 85 85 87 97 76 88 77 87 88
初三级 82 80 78 78 96 97 88 89 86
(1)请填写下表:(占3分)
平均数 众数 中位数
初一年级
初二年级
初三年级
(2)如果在每个年级的选手中分别选出3人参加决赛,你认为哪个年级的实力更加强一些,说明理由。
25. 某市举办“2008拥抱北京”迎奥运长跑活动,参加长跑活动的市民约有10 000人,为了解参加长跑活动人员的年龄分布情况,从中随机抽取了一部分人的年龄作为样本,进行数据处理后,得到如图所示不完整的频数分布直方图.
(1)若所抽取年龄在60岁以上的人数占样本总人数的15%,请求出样本容量,并补全频数分布直方图;
(2)请估计参加这次长跑活动的市民中,20岁以下的约有多少人
(3)根据统计图提供的信息,请再写出两条正确的结论.
26. 下图是某班学生上学的三种方式(乘车、步行、骑车)的人数分布直方图和扇形图.
(1)求该班有多少名学生;
(2)补上人数分布直方图的空缺部分;
(3)若全年级有800人, 估计该年级步行人数.
参考答案(仅供参考)
一.选择题
1 2 3 4 5 6 7 8 9 10
B A D A A B B C A D
二.填空题
11. 26
12. 8
13. 9, 8
14. 7
15. 12.6
16. 20000
17. 8.04
18. 65,2/13,略
三.解答题答案:
19. (1)平均数320件,中位数210件,众数210件
(2)不合理. 因为15人中有13人的销售额不到320件,320件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平,销售额定为210件合适些,因为210件既是中位数,又是众数,是大部分人能达到的定额.
20. (1)6、7、8 (2)甲、乙的平均分数都是7且S2甲 < S2乙 如果我是教练,我会选甲运动员参加比赛
21. (1)100名
(2)360
(3)如右图
22. (1)略;(2) 76%;(3)该校学生的数学学习情况较好
23. (1)设P1. P4. P8顺次为3个班考评分的平均数;
W1. W4. W8顺次为3个班考评分的中位数;
Z1. Z4. Z8 顺次为3个班考评分的众数.
则:P1=(10+10+6+10+7)=8.6分),
P4=(8+8+8+9+10)=8.6(分),
P8=(9+10+9+6+9)=8.6(分).
W1=10(分),W4=8(分),W8=9(分).
(Z1=10(分),Z4=8(分),Z8=9(分)).
∴平均数不能反映这3个班的考评结果的差异,而用中位数(或众数)能反映差异,
且W1>W8>W4(Z1>Z8>Z4).
(2)(给出一种参考答案)选定:
行为规范:学习成绩:校运动会:艺术获奖:劳动卫生=3:2:3:1:1
设K1. K4. K8顺次为3个班的考评分,则:
K1=0.3×10+0.2×10+0.3×6+0.1×10+0.1×7=8.5,
K4=0.3×10+0.2×8+0.3×8+0.1×9+0.1×8=8.7,
K8=0.3×9+0.2×10+0.3×9+0.1×6+0.1×9=8.9.
∵K8>K4>K1,∴推荐初三(8)班为市级先进班集体的候选班.
24. (1)80、86、85.5
(2)∵初一、初二、初三各级前三名学生决赛成绩的平均数分别是93分、91分94分
∴从各年级参加决赛的选手中分别选队参加决赛初三级实力更强
25. (1)15÷15%=100,
∴样本容量是100。补图如下:
(2)10 000×28%=2800(人),
∴参加这次长跑活动的市民中20岁以下的约有2800人.(6分)
(3)答案不唯一,例如所得的信息可以是:
①参加这次长跑活动的市民中20岁以下的人最多;
②参加这次长跑活动的市民中41~50岁之间的人最少;
参加这次长跑活动的市民中20~30岁之间的人大约是15%:等等
26. (1)该班有学生: 25÷50%=50(人) (2分)
(2) (4分)
(3)该年级步行人数约为: 800×20%=160(人) (7分)
0
1
2
3
4
5
6
7
8
等待时间/min
4
8
12
16
人数
2
3
6
8
16
9
5
2
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
学生数
做对题数
5
10
4
20
10
9
8
7
20
8
18
15
0
(第14题)
人数
50
40
30
20
10
O
阅读 运动 娱乐 其他 项目
运动
20%
娱乐
40%
阅读
其他
分组 频数 频率
49.5~59.5 0.04
59.5~69.5 3 0.06
7 0.14
79.5~89.5
89.5~99.5 21 0.42
49. 5
59. 5
69. 5
79. 5
89. 5
99. 5
分数
学号________. 姓名________.
一.选择题 (每小题4分,共40分)
1. 超市为了制定某个时间段收银台开放方案,统计了这个
时间段本超市顾客在收银台排队付款的等待时间,并绘制成
如下的频数分布直方图(图中等待时间6分钟到7分钟表示
大于或等于6分钟而小于7分钟,其它类同).这个时间段内
顾客等待时间不少于6分钟的人数为
A.5 B.7 C.16 D.33
2. 下列调查中适合用普查方法的是
A.要了解本班同学的身高 B.要了解一批灯泡的使用寿命
C.要了解全国人口老龄化的情况 D.要了解电视台某娱乐节目的收视率
3. 右边给出的是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,请你运用方程思想来研究,发现这三个数的和不可能是
A. 69 B. 54 C. 27 D.40
4. 某青年排球队12名队员的年龄情况如下:
年龄(单位:岁) 18 19 20 21 22
人 数 1 4 3 2 2
则这个队队员年龄的众数和中位数是
A.19,20 B.19,19 C.19,20.5 D.20,19
5. 某市对2400名年满15岁的男生的身高进行了测量,结果身高(单位:m)在1.68~1.70这一小组的频率为0.25,则该组的人数为
A. 600人 B. 150 人 C.60人 D. 15人
6. “五一”黄金周期间,为了促销商品,甲、乙两个商店都采取优惠措施,甲店推出八折后再打八折,乙店则一次性六折优惠,对于同一种商品,下列结论正确的是
A.甲比乙优惠; B.乙比甲优惠;
C.两店同样优惠; D.无法比较两店的优惠程度。
7. 举世瞩目的三峡大坝于今年5月全线建成,所装发电机组全部投入运行后,预计年发电量可以达到847亿度,用科学记数法表示这个发电量为
A.847×108度 B.8.47×1010度 C.8.47×1012度 D.84.7×101010度
8. 为筹备班级的初中毕业联欢会, 班长对全班同学爱吃哪几种水果作民意调查, 从而最终决定买什么水果。下列调查数据中最值得关注的是
A. 平均数 B. 中位数 C. 众数 D. 方差
9. 如图是某地区用水量与人口数情况统计表,日平均用水量为400万吨的这一年,人口数大约是
A.180万 B.200万 C.300万 D.400万
10. 从一幅扑克牌中抽出5张红桃,4张梅花,3张黑桃放在一起洗匀后,从中一次随机抽出10张,恰好红桃.梅花.黑桃3种牌都抽到,这件事情
A.可能发生 B.不可能发生 C.很可能发生 D.必然发生
二.填空题 (每小题3分,共24分)
11. 数据22,24,21,28,37,26,30的中位数是________.
12. 一射击运动员在一次射击练习中打出的成绩是(单位:环):7,8,9,8,6,8,10,7,这组数据的众数是_________环
13. 数学老师布置10道选择题作为课堂练习,科代表将全班同学的答题情况绘制成条形统计图,根据图中信息,全班每位同学答对题数的中位数和众数分别为______________.
14. 某商场为了解本商场的服务质量,随机调查了本商场的100名顾客,调查的结果如图所示. 根据图中给出的信息,这100名顾客中对该商场的服务质量表示不满意的有 人.
15. 为了解某校九年级学生的营养状况,随机抽取了8位学生的血样进行血色素检测,以此来估计这个年级学生的平均水平,测得结果如下(单位:克):13.8,12.5,10.6,11,14.7,12.4,13.6,12.2,则这8位学生血色素的平均值为____克.
16. 为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有10条,则估计池塘里有鱼______________条.
17. 近年来,义乌市对外贸易快速增长.右图是根据我市2004年至2007年出口总额绘制的条形统计图,观察统计图可得在这期间我市年出口总额的极差是________亿美元.
18. 某校九年级三班在体育毕业考试中,全班所有学生得分的情况如下表所示:那么该班共有_________ 人,随机地抽取1人,恰好是获得30分的学生的概率是 ,从下表中,你还能获取的信息是 (写出一条即可).
分数段 18分以下 18—20分 21-23分 24-26分 27—29分 30分
人数 2 3 12 20 18 10
三.解答题 (共56分)
19. 某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员该月销售量的平均数、中位数和众数;
(2)假设销售负责人把每位营销员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.
20. 射击集训队在一个月集训中,对甲、乙两名运动员进行了10次测试,成绩如下:(5分)
次数 1 2 3 4 5 6 7 8 9 10
甲(环数) 9 6 6 8 7 6 6 8 8 6
乙(环数) 4 5 7 6 8 7 8 8 8 9
根据表中提供的信息,填写下表:(3分)
平均数 方差 众数
甲 7 1.2
乙 2.2
(2)如果你是教练,会选哪位运动员参加比赛,请说明理由。(3分)
21. 其中学团委会为研究该校学生的课余活动情况,采取抽样的方法,从阅读、运动、娱乐、其他等四个方面调查了若干名学生的兴趣爱好,并将调查的结果绘制了如下的两幅不完整的统计图(如图1、图2),请你根据图中提供的信息解答下列问题:
(1)在这次研究中,一共调查了多少名学生?
(2)“其他”在扇形图中所占的圆心角是多少度?
(3)补全频数分布折线图。
22. 某中学为了了解初中三年级数学的学习情况,在全校学生中抽取了50名学生进行
测试(成绩均为整数,满分为100分),列出频率分布表和频率分布直方图如下所示:
(1)完成频率分布表和频率直方图中未完成的部分(可直接填入表中或画在直方图上)
(2)本次测试这50名学生的优秀率是多少?(成绩不低于80分为优秀)
(3)请你对该校学生的数学学习情况作一个简单的评价(字数在20字以内)
23. 某学校对初中毕业班经过初步比较后,决定从初三(1). (4). (8)班这三个班中推荐一个班为市级先进班集体的候选班.现对这三个班进行综合素质考评,下表是它们五项素质考评的得分表(以分为单位,每项满分为10分).
班级 行为规范 学习成绩 校运动会 艺术获奖 劳动卫生
初三(1)班 10 10 6 10 7
初三(4)班 10 8 8 9 8
初三(8)班 9 10 9 6 9
(1)请问各班五项考评分的平均数. 中位数和众数中哪个统计量不能反映三个班的考评结果的差异?并从中选择一个能反映差异的统计量将他们得分进行排序;
(2)根据你对表中五个项目的重要程度的认识,设定一个各项考评内容的占分比例(比例的各项须满足:①均为整数;②总和为10;③不全相同),按这个比例对各班的得分重新计算,比较出大小关系,并从中推荐一个得分最高的班级作为市级先进班集体的候选班.
24. 为了普及环保知识,增强环保意识,某中学组织了一次环保知识竞赛活动,初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这此选手的决赛成绩(满分100分)如下表:
决赛成绩(单位:分)
初一级 80 86 88 80 99 80 74 91 89
初二级 85 85 87 97 76 88 77 87 88
初三级 82 80 78 78 96 97 88 89 86
(1)请填写下表:(占3分)
平均数 众数 中位数
初一年级
初二年级
初三年级
(2)如果在每个年级的选手中分别选出3人参加决赛,你认为哪个年级的实力更加强一些,说明理由。
25. 某市举办“2008拥抱北京”迎奥运长跑活动,参加长跑活动的市民约有10 000人,为了解参加长跑活动人员的年龄分布情况,从中随机抽取了一部分人的年龄作为样本,进行数据处理后,得到如图所示不完整的频数分布直方图.
(1)若所抽取年龄在60岁以上的人数占样本总人数的15%,请求出样本容量,并补全频数分布直方图;
(2)请估计参加这次长跑活动的市民中,20岁以下的约有多少人
(3)根据统计图提供的信息,请再写出两条正确的结论.
26. 下图是某班学生上学的三种方式(乘车、步行、骑车)的人数分布直方图和扇形图.
(1)求该班有多少名学生;
(2)补上人数分布直方图的空缺部分;
(3)若全年级有800人, 估计该年级步行人数.
参考答案(仅供参考)
一.选择题
1 2 3 4 5 6 7 8 9 10
B A D A A B B C A D
二.填空题
11. 26
12. 8
13. 9, 8
14. 7
15. 12.6
16. 20000
17. 8.04
18. 65,2/13,略
三.解答题答案:
19. (1)平均数320件,中位数210件,众数210件
(2)不合理. 因为15人中有13人的销售额不到320件,320件虽是所给一组数据的平均数,它却不能很好地反映销售人员的一般水平,销售额定为210件合适些,因为210件既是中位数,又是众数,是大部分人能达到的定额.
20. (1)6、7、8 (2)甲、乙的平均分数都是7且S2甲 < S2乙 如果我是教练,我会选甲运动员参加比赛
21. (1)100名
(2)360
(3)如右图
22. (1)略;(2) 76%;(3)该校学生的数学学习情况较好
23. (1)设P1. P4. P8顺次为3个班考评分的平均数;
W1. W4. W8顺次为3个班考评分的中位数;
Z1. Z4. Z8 顺次为3个班考评分的众数.
则:P1=(10+10+6+10+7)=8.6分),
P4=(8+8+8+9+10)=8.6(分),
P8=(9+10+9+6+9)=8.6(分).
W1=10(分),W4=8(分),W8=9(分).
(Z1=10(分),Z4=8(分),Z8=9(分)).
∴平均数不能反映这3个班的考评结果的差异,而用中位数(或众数)能反映差异,
且W1>W8>W4(Z1>Z8>Z4).
(2)(给出一种参考答案)选定:
行为规范:学习成绩:校运动会:艺术获奖:劳动卫生=3:2:3:1:1
设K1. K4. K8顺次为3个班的考评分,则:
K1=0.3×10+0.2×10+0.3×6+0.1×10+0.1×7=8.5,
K4=0.3×10+0.2×8+0.3×8+0.1×9+0.1×8=8.7,
K8=0.3×9+0.2×10+0.3×9+0.1×6+0.1×9=8.9.
∵K8>K4>K1,∴推荐初三(8)班为市级先进班集体的候选班.
24. (1)80、86、85.5
(2)∵初一、初二、初三各级前三名学生决赛成绩的平均数分别是93分、91分94分
∴从各年级参加决赛的选手中分别选队参加决赛初三级实力更强
25. (1)15÷15%=100,
∴样本容量是100。补图如下:
(2)10 000×28%=2800(人),
∴参加这次长跑活动的市民中20岁以下的约有2800人.(6分)
(3)答案不唯一,例如所得的信息可以是:
①参加这次长跑活动的市民中20岁以下的人最多;
②参加这次长跑活动的市民中41~50岁之间的人最少;
参加这次长跑活动的市民中20~30岁之间的人大约是15%:等等
26. (1)该班有学生: 25÷50%=50(人) (2分)
(2) (4分)
(3)该年级步行人数约为: 800×20%=160(人) (7分)
0
1
2
3
4
5
6
7
8
等待时间/min
4
8
12
16
人数
2
3
6
8
16
9
5
2
日 一 二 三 四 五 六
1 2 3 4 5 6
7 8 9 10 11 12 13
14 15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31
学生数
做对题数
5
10
4
20
10
9
8
7
20
8
18
15
0
(第14题)
人数
50
40
30
20
10
O
阅读 运动 娱乐 其他 项目
运动
20%
娱乐
40%
阅读
其他
分组 频数 频率
49.5~59.5 0.04
59.5~69.5 3 0.06
7 0.14
79.5~89.5
89.5~99.5 21 0.42
49. 5
59. 5
69. 5
79. 5
89. 5
99. 5
分数
