1.4.1 用空间向量研究直线、平面的位置关系-【新教材】人教A版(2019)高中数学选择性必修第一册同步练习(Word含答案解析)
文档属性
| 名称 | 1.4.1 用空间向量研究直线、平面的位置关系-【新教材】人教A版(2019)高中数学选择性必修第一册同步练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 108.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 22:30:56 | ||
图片预览




文档简介
用空间向量研究直线、平面的位置关系同步练习
一、选择题
若直线l的方向向量a=(1,2,?1),平面α的一个法向量m=(?2,?4,k),若l⊥α,则实数k=(??? )
A. 2 B. ?10 C. ?2 D. 10
设l1的方向向量为a=(1,2,?2),l2的方向向量为b=(?2,3,m),若l1⊥l2,则m等于(??? )
A. 1 B. 2 C. 12 D. 3
若直线l的方向向量为(2,1,m),平面α的法向量为(1,12,2),且l⊥α,则m=(????)
A. 2 B. 3 C. 4 D. 5
已知AB=(1,5,?2),BC=(3,1,z),若AB⊥BC,BP=(x?1,y,?3),且BP⊥平面ABC,则实数x、y、z分别为( )
A. 337,?157,4 B. 407,?157,4 C. 407,?2,4 D. 4,407,?15
已知O为坐标原点,向量a=?2,1,1,点A?3,?1,4,B?2,?2,2.若点E在直线AB上,且OE⊥a,则点E的坐标为(??? )
A. ?65,?145,25 B. 65,145,?25 C. 65,?145,25 D. ?65,145,?25
如图,在正方体ABCD?A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是(? ?)
A. MN⊥CC1 B. MN⊥平面ACC1A1
C. MN//平面ABCD D. MN//A1B1
平面α的法向量u=(2,?2,2),平面β的法向量v=(1,2,1),则下列命题正确的是( )
A. α,β平行 B. α,β垂直 C. α,β重合 D. α,β不垂直
若直线l的方向向量为a,平面α的法向量为n,能使l//α的是( )
A. a=(1,0,1),n=(?1,0,?1)
B. a=(1,3,5),n=(1,0,1)
C. a=(0,2,1),n=(?2,1,0)
D. a=(1,?1,3),n=(0,3,1)
若平面α的一个法向量为(1,2,0),平面β的一个法向量为(2,?1,0),则平面α和平面β的位置关系是( )
A. 平行 B. 相交但不垂直 C. 垂直 D. 重合
如图,在三棱锥P?ABC中,PA⊥平面ABC,∠ABC=90°,∠BAC=60°,PA=AB=2,以点B为原点,分别以BC,BA,AP的方向为x,y,z轴的正方向,建立空间直角坐标系,设平面PAB和平面PBC的法向量分别为m和n,则下面选项中正确的是(? ? ?)
A. 点P的坐标为(0,0,2) B. PC=(4,0,?2)
C. n可能为(0,?2,2) D. cosm,n>0
平面α的法向量u=(x,1,?2),平面β的法向量ν=(?1,y,12),已知α//β,则x+y等于(??? )
A. 154 B. 174 C. 3 D. 52
若平面α,β的法向量分别为u=(?2,3,?5),v=(3,?1,4),则(????)
A. α//β B. α⊥β
C. α,β相交但不垂直 D. 以上均不正确
二、填空题
已知点A(1,4,1),B(2,3,1),C(3,2,0),若直线l⊥平面ABC,直线l的方向向量为a=(2,m,k),则m=________.
已知直线l的一个方向向量d=(2,3,5),平面α的一个法向量u=(?4,m,n),若l⊥α,则m+n=______.
设u,v分别是平面α,β的法向量,u=(1,2,?2),v=(?2,?4,m).若α?//?β,则实数m=___________.
在空间直角坐标系O?xyz中,已知平面α的一个法向量是n=(1,?1,2),且平面α过点A(0,3,1).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是__________________.
三、解答题
如图所示,在四棱锥P?ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.用空间向量知识证明:
(1)CM?//平面PAD;????????
(2)平面PAB⊥平面PAD.
如图,在正方体ABCD?A1B1C1D1中,E,F分别为底面A1B1C1D1和侧面B1C1CB的中心.
求证:(1)EF//A1B;
(2)EF//平面A1BD;
(3)平面B1EF//平面A1BD.?
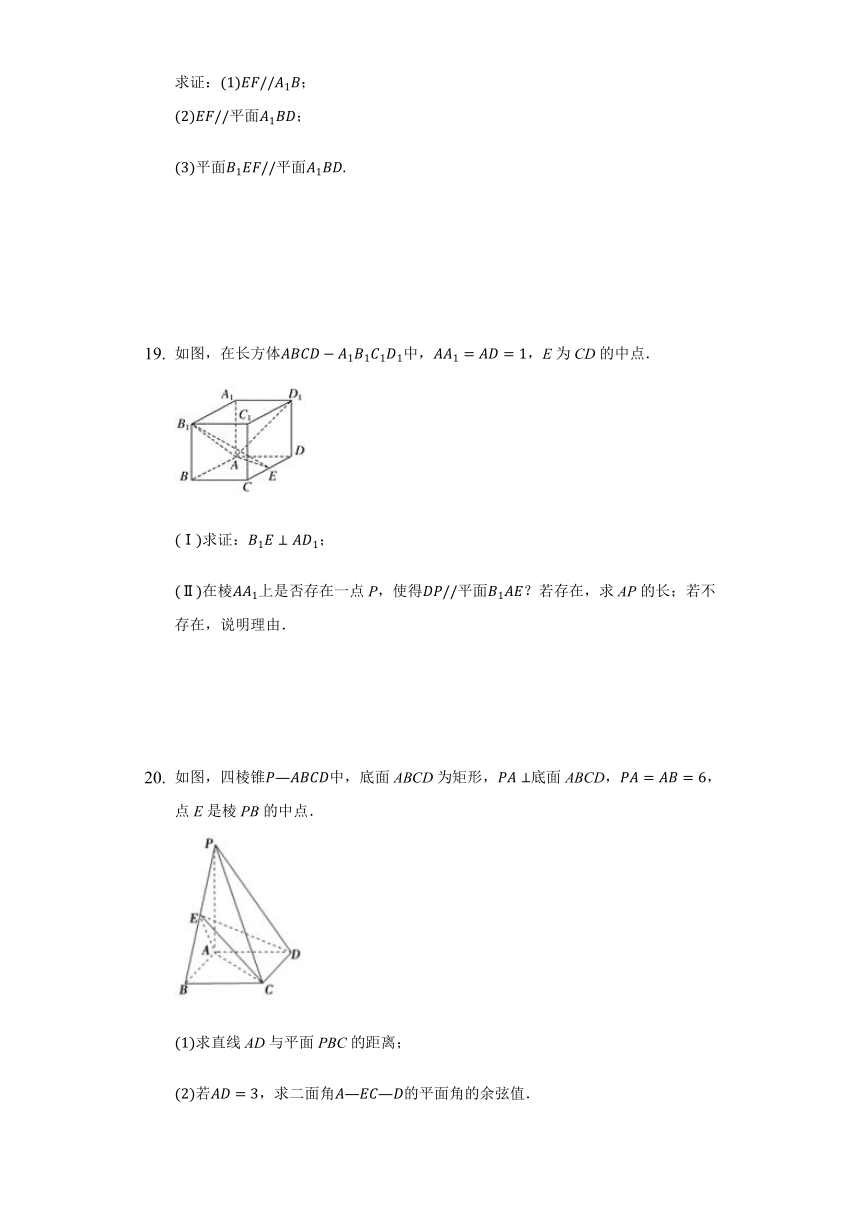
如图,在长方体ABCD?A1B1C1D1中,AA1=AD=1,E为CD的中点.
(Ⅰ)求证:B1E⊥AD1;
(Ⅱ)在棱AA1上是否存在一点P,使得DP//平面B1AE?若存在,求AP的长;若不存在,说明理由.
如图,四棱锥P—ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=6,点E是棱PB的中点.
(1)求直线AD与平面PBC的距离;
(2)若AD=3,求二面角A—EC—D的平面角的余弦值.
答案和解析
1.【答案】A
【解析】
解:∵直线l的方向向量a=(1,2,?1),
平面α的一个法向量m=(?2,?4,k),l⊥α,
∴a//m,
∴1?2=2?4=?1k,解得k=2.
故选A.
2.【答案】B
【解答】
解:∵l1⊥l2,∴a·b=1×?2+2×3?2m=0,
解得m=2,
故选B.
3.【答案】C
【解答】
解:因为直线l的方向向量为(2,1,m),平面α的法向量为(1,12,2),且l⊥α,
所以存在实数λ,使得(2,1,m)=λ(1,12,2),
所以2=λ1=12λm=2λ,
解得λ=2,m=4.
故选C.
4.【答案】B
【解答】
解:∵AB⊥BC,
∴AB?BC=3+5?2z=0,解得z=4.
∴BC=(3,1,4).
∵BP⊥平面ABC,AB?平面ABC,BC?平面ABC,
∴BP⊥AB,BP⊥BC,
∴BP⊥AB,BP⊥BC.
∴BP?AB=x?1+5y+6=0BP?BC=3(x?1)+y?12=0,
解得x=407y=?157.
∴x=407,y=?157,z=4.
故选:B.
5.【答案】A
【解答】
解:∵点E在直线AB上,故OE=OA+AE=OA+tAB=(?3,?1,4)+t(1,?1,?2)=(?3+t,?1?t,4?2t),
且OE⊥a,,
故点E的坐标为?65,?145,25,
故选A.
6.【答案】D
【解答】
解:如图,建立空间直角坐标系:
设正方体棱长为2,
则A(2,0,0),B(2,2,0),C10,2,2,
M(1,2,1),D10,0,2,C(0,2,0),N(0,1,1),
则MN=?1,?1,0,CC1=0,0,2,
AC=?2,2,0,AB=0,2,0,
∴MN·CC1=0,∴MN⊥CC1,故A正确;
∵MN·AC=0,AC⊥MN,
∵AC∩CC1=C,AC,CC1?平面ACC1A1,
∴MN⊥平面ACC1A1,故B正确;
根据AB=0,2,0,MN=?1,?1,0,
可知,MN和AB不平行,故MN和A1B1不平行,故D错误;
易求得平面ABCD的一个法向量为n=0,0,1,
则MN·n=0,又MN?平面ABCD,
∴MN?//平面ABCD,故C正确.
故选D.
7.【答案】B
【解析】解:平面α的法向量u=(2,?2,2),平面β的法向量v=(1,2,1),
因为u?v=2?4+2=0,
所以两个平面垂直.
8.【答案】D
【解答】
解:若l//α,则a→·n→=0,
经验证只有选项D中a→·n→=0,
故选D.
9.【答案】C
【解答】
解:由题意可得(1,2,0)?(2,?1,0)
=1×2?2×1+0×0=0,
故两个平面的法向量垂直,故平面α和平面β的位置关系为垂直,
故选C.
10.【答案】C
【解答】
解:由题意可得B(0,0,0),A(0,2,0),C(23,0,0),P(0,2,2),
所以PC=(23,?2,?2),BP=(0,2,2).
设n=(x,y,z),则23x?2y?2z=02z+2y=0.,
取z=2,可得n=(0,?2,2).
因为AB⊥BC,PA⊥BC,所以BC⊥平面PAB,
所以平面PBC⊥平面PAB,所以,
所以cos=0.
综上所述,A,B,D错,C正确.
故选C.
11.【答案】A
【解答】
解:由题意知,∵α//β,∴u=λν,
即x=?λ,1=λy,?2=12λ,解得λ=?4,y=?14,x=4,
∴x+y=4?14=154.
故选A.
12.【答案】C
【解答】
解:因为u=(?2,3,?5),v=(3,?1,4),
所以u与v不平行且u与v不垂直,
故选C.
13.【答案】2
【解答】
解:由题意知a是平面ABC的一个法向量,
∵AB=(1,?1,0),AC=(2,?2,?1),
∴2×1+m×(?1)+k×0=0,2×2+m×(?2)+k×(?1)=0,解得m=2.
故答案为2.
14.【答案】?16
【解答】
解:因为直线l的一个方向向量d=(2,3,5),平面α的一个法向量u=(?4,m,n),l⊥α,则有d=(2,3,5)和u=(?4,m,n)平行,故有?42=m3=n5,解之得m=?6,n=?10,则m+n=?16.故答案为?16.
15.【答案】4
【解答】
解:因为α?//β,所以u//v,
即1?2=2?4=?2m,
解得m=4.
故答案为4.
16.【答案】x?y+2z+1=0
【解答】
解:由题意知AP⊥n,
所以AP·n=0,
因为AP=x,y?3,z?1,n=(1,?1,2),
所以x?y?3+2z?1=0,
即x?y+2z+1=0.
故答案为x?y+2z+1=0.
17.【答案】证明:以C为坐标原点,CB所在直线为x轴,CD所在直线为y轴,CP所在直线为z轴,建立如图所示的空间直角坐标系Cxyz.
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABCD所成的角,
∴∠PBC=30°.
∵PC=2,∴BC=23,PB=4,
∴D(0,1,0),B(23,0,0),A(23,4,0),P(0,0,2),M,
∴DP=(0,?1,2),DA=(23,3,0),
CM=(32,0,32).
(1)方法一令n=(x,y,z)为平面PAD的法向量,则DP·n=0DA·n=0即?y+2z=0,23x+3y=0,∴z=12yx=?32y
令y=2,得n=(?3,2,1).
∵n·CM=?3×32+2×0+1×32=0,∴n⊥CM.
又CM?平面PAD,∴CM?//平面PAD.
方法二∵PD=(0,1,?2),PA=(23,4,?2).
令CM=xPD+yPA,
则32=23y0=x+4y,32=?2x?2y,解方程组得x=?1,y=14
∴CM=?PD+14PA.
由共面向量定理知CM与PD,PA共面,
又∵CM?平面PAD,
∴CM?//平面PAD.
(2)取AP的中点E,连接BE,
则E(3,2,1),BE=(?3,2,1).
∵PB=AB,∴BE⊥PA.
又∵BE·DA=(?3,2,1)·(23,3,0)=0,
∴BE⊥DA,∴BE⊥DA,又PA∩DA=A,
PA,DA?平面PAD,
∴BE⊥平面PAD,又∵BE?平面PAB,
∴平面PAB⊥平面PAD.
18.【答案】证明:以点D为原点,DA,DC,DD1分别为x轴、y轴、z轴,建立空间直角坐标系,
令正方体的棱长为2,则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,2),E(1,1,2),F(1,2,1),
(1)EF→=(0,1,?1),A1B→=(0,2,?2),
因为A1B→=2EF→,所以A1B→//EF→,
所以EF//A1B;
(2)设平面A1BD的一个法向量为m→=(x,y,z),
则A1B→·m→=0,DB→·m→=0,
即2y?2z=0,2x+2y=0,令x=1,则m=(1,?1,?1),
因为m→·EF→=0,
所以EF//平面A1BD;
(3)由(2),同理求出平面EFB1的一个法向量n=(1,?1,?1),
所以平面B1EF//平面A1BD.
19.【答案】解:以A为原点,AB,AD,AA1?的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,设AB=a.
(Ⅰ)证明:A(0,0,0),D(0,1,0),D1(0,1,1),Ea2,1,0,B1(a,0,1),
故AD1=(0,1,1),B1E=?a2,1,?1,
因为B1E·AD1=?a2×0+1×1+(?1)×1=0,所以B1E⊥AD1.
(Ⅱ)假设在棱AA1上存在一点P(0,0,z0),使得DP//平面B1AE,
此时DP=(0,?1,z0),
再设平面B1AE的一个法向量为n=(x,y,z),
AB1=(a,0,1),AE=a2,1,0.
因为n⊥平面B1AE,
所以n⊥AB1,n⊥AE,即ax+z=0,ax2+y=0,
取x=1,得y=?a2,z=?a,得平面B1AE的一个法向量n=1,?a2,?a.
要使DP//平面B1AE,只要n⊥DP,有a2?az0=0,解得z0=12.
又DP?平面B1AE,所以存在点P,满足DP//平面B1AE,此时AP=12.
20.【答案】解:(1)如图,以A为坐标原点,射线AB、AD、AP分别为x轴、y轴、z轴正半轴,建立空间直角坐标系A?xyz.
设D(0,a,0),则B(6,0,0),C(6,a,0),P(0,0,6),E(62,0,62).
因此,AE=(62,0,62),BC=(0,a,0),PC=(6,a,?6).
则AE?BC=0,AE?PC=0,
所以AE⊥BC,AE⊥PC,又BC∩PC=C,所以AE⊥平面PBC.
由AD//BC,AD?平面PBC,BC?平面PBC,所以AD//平面PBC.
故直线AD与平面PBC的距离为点A到平面PBC的距离,即为|AE|=3.
(2)设平面AEC的法向量为n1=(x1,y1,z1).
因为AE=(62,0,62),AC=(6,3,0).
所以62x1+62z1=06x1+3y1=0,令x1=?1,得y1=2,z1=1,所以n1=(?1,2,1).
设平面EDC的法向量为n2=(x2,y2?z2),
因为EC=(62,3,?62),CD=(?6,0,0),
所以62x2+3y2?62z2=0?6x2=0,令z2=2,得y2=1,所以n2=(0,1,2).
由图可知二面角A?EC?D的平面角为一锐角,
所以二面角A?EC?D的平面角θ的余弦值为:cosθ=n1·n2n1·n2=222×3=63.
一、选择题
若直线l的方向向量a=(1,2,?1),平面α的一个法向量m=(?2,?4,k),若l⊥α,则实数k=(??? )
A. 2 B. ?10 C. ?2 D. 10
设l1的方向向量为a=(1,2,?2),l2的方向向量为b=(?2,3,m),若l1⊥l2,则m等于(??? )
A. 1 B. 2 C. 12 D. 3
若直线l的方向向量为(2,1,m),平面α的法向量为(1,12,2),且l⊥α,则m=(????)
A. 2 B. 3 C. 4 D. 5
已知AB=(1,5,?2),BC=(3,1,z),若AB⊥BC,BP=(x?1,y,?3),且BP⊥平面ABC,则实数x、y、z分别为( )
A. 337,?157,4 B. 407,?157,4 C. 407,?2,4 D. 4,407,?15
已知O为坐标原点,向量a=?2,1,1,点A?3,?1,4,B?2,?2,2.若点E在直线AB上,且OE⊥a,则点E的坐标为(??? )
A. ?65,?145,25 B. 65,145,?25 C. 65,?145,25 D. ?65,145,?25
如图,在正方体ABCD?A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列判断错误的是(? ?)
A. MN⊥CC1 B. MN⊥平面ACC1A1
C. MN//平面ABCD D. MN//A1B1
平面α的法向量u=(2,?2,2),平面β的法向量v=(1,2,1),则下列命题正确的是( )
A. α,β平行 B. α,β垂直 C. α,β重合 D. α,β不垂直
若直线l的方向向量为a,平面α的法向量为n,能使l//α的是( )
A. a=(1,0,1),n=(?1,0,?1)
B. a=(1,3,5),n=(1,0,1)
C. a=(0,2,1),n=(?2,1,0)
D. a=(1,?1,3),n=(0,3,1)
若平面α的一个法向量为(1,2,0),平面β的一个法向量为(2,?1,0),则平面α和平面β的位置关系是( )
A. 平行 B. 相交但不垂直 C. 垂直 D. 重合
如图,在三棱锥P?ABC中,PA⊥平面ABC,∠ABC=90°,∠BAC=60°,PA=AB=2,以点B为原点,分别以BC,BA,AP的方向为x,y,z轴的正方向,建立空间直角坐标系,设平面PAB和平面PBC的法向量分别为m和n,则下面选项中正确的是(? ? ?)
A. 点P的坐标为(0,0,2) B. PC=(4,0,?2)
C. n可能为(0,?2,2) D. cosm,n>0
平面α的法向量u=(x,1,?2),平面β的法向量ν=(?1,y,12),已知α//β,则x+y等于(??? )
A. 154 B. 174 C. 3 D. 52
若平面α,β的法向量分别为u=(?2,3,?5),v=(3,?1,4),则(????)
A. α//β B. α⊥β
C. α,β相交但不垂直 D. 以上均不正确
二、填空题
已知点A(1,4,1),B(2,3,1),C(3,2,0),若直线l⊥平面ABC,直线l的方向向量为a=(2,m,k),则m=________.
已知直线l的一个方向向量d=(2,3,5),平面α的一个法向量u=(?4,m,n),若l⊥α,则m+n=______.
设u,v分别是平面α,β的法向量,u=(1,2,?2),v=(?2,?4,m).若α?//?β,则实数m=___________.
在空间直角坐标系O?xyz中,已知平面α的一个法向量是n=(1,?1,2),且平面α过点A(0,3,1).若P(x,y,z)是平面α上任意一点,则点P的坐标满足的方程是__________________.
三、解答题
如图所示,在四棱锥P?ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠ABC=∠BCD=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.用空间向量知识证明:
(1)CM?//平面PAD;????????
(2)平面PAB⊥平面PAD.
如图,在正方体ABCD?A1B1C1D1中,E,F分别为底面A1B1C1D1和侧面B1C1CB的中心.
求证:(1)EF//A1B;
(2)EF//平面A1BD;
(3)平面B1EF//平面A1BD.?
如图,在长方体ABCD?A1B1C1D1中,AA1=AD=1,E为CD的中点.
(Ⅰ)求证:B1E⊥AD1;
(Ⅱ)在棱AA1上是否存在一点P,使得DP//平面B1AE?若存在,求AP的长;若不存在,说明理由.
如图,四棱锥P—ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=AB=6,点E是棱PB的中点.
(1)求直线AD与平面PBC的距离;
(2)若AD=3,求二面角A—EC—D的平面角的余弦值.
答案和解析
1.【答案】A
【解析】
解:∵直线l的方向向量a=(1,2,?1),
平面α的一个法向量m=(?2,?4,k),l⊥α,
∴a//m,
∴1?2=2?4=?1k,解得k=2.
故选A.
2.【答案】B
【解答】
解:∵l1⊥l2,∴a·b=1×?2+2×3?2m=0,
解得m=2,
故选B.
3.【答案】C
【解答】
解:因为直线l的方向向量为(2,1,m),平面α的法向量为(1,12,2),且l⊥α,
所以存在实数λ,使得(2,1,m)=λ(1,12,2),
所以2=λ1=12λm=2λ,
解得λ=2,m=4.
故选C.
4.【答案】B
【解答】
解:∵AB⊥BC,
∴AB?BC=3+5?2z=0,解得z=4.
∴BC=(3,1,4).
∵BP⊥平面ABC,AB?平面ABC,BC?平面ABC,
∴BP⊥AB,BP⊥BC,
∴BP⊥AB,BP⊥BC.
∴BP?AB=x?1+5y+6=0BP?BC=3(x?1)+y?12=0,
解得x=407y=?157.
∴x=407,y=?157,z=4.
故选:B.
5.【答案】A
【解答】
解:∵点E在直线AB上,故OE=OA+AE=OA+tAB=(?3,?1,4)+t(1,?1,?2)=(?3+t,?1?t,4?2t),
且OE⊥a,,
故点E的坐标为?65,?145,25,
故选A.
6.【答案】D
【解答】
解:如图,建立空间直角坐标系:
设正方体棱长为2,
则A(2,0,0),B(2,2,0),C10,2,2,
M(1,2,1),D10,0,2,C(0,2,0),N(0,1,1),
则MN=?1,?1,0,CC1=0,0,2,
AC=?2,2,0,AB=0,2,0,
∴MN·CC1=0,∴MN⊥CC1,故A正确;
∵MN·AC=0,AC⊥MN,
∵AC∩CC1=C,AC,CC1?平面ACC1A1,
∴MN⊥平面ACC1A1,故B正确;
根据AB=0,2,0,MN=?1,?1,0,
可知,MN和AB不平行,故MN和A1B1不平行,故D错误;
易求得平面ABCD的一个法向量为n=0,0,1,
则MN·n=0,又MN?平面ABCD,
∴MN?//平面ABCD,故C正确.
故选D.
7.【答案】B
【解析】解:平面α的法向量u=(2,?2,2),平面β的法向量v=(1,2,1),
因为u?v=2?4+2=0,
所以两个平面垂直.
8.【答案】D
【解答】
解:若l//α,则a→·n→=0,
经验证只有选项D中a→·n→=0,
故选D.
9.【答案】C
【解答】
解:由题意可得(1,2,0)?(2,?1,0)
=1×2?2×1+0×0=0,
故两个平面的法向量垂直,故平面α和平面β的位置关系为垂直,
故选C.
10.【答案】C
【解答】
解:由题意可得B(0,0,0),A(0,2,0),C(23,0,0),P(0,2,2),
所以PC=(23,?2,?2),BP=(0,2,2).
设n=(x,y,z),则23x?2y?2z=02z+2y=0.,
取z=2,可得n=(0,?2,2).
因为AB⊥BC,PA⊥BC,所以BC⊥平面PAB,
所以平面PBC⊥平面PAB,所以,
所以cos
综上所述,A,B,D错,C正确.
故选C.
11.【答案】A
【解答】
解:由题意知,∵α//β,∴u=λν,
即x=?λ,1=λy,?2=12λ,解得λ=?4,y=?14,x=4,
∴x+y=4?14=154.
故选A.
12.【答案】C
【解答】
解:因为u=(?2,3,?5),v=(3,?1,4),
所以u与v不平行且u与v不垂直,
故选C.
13.【答案】2
【解答】
解:由题意知a是平面ABC的一个法向量,
∵AB=(1,?1,0),AC=(2,?2,?1),
∴2×1+m×(?1)+k×0=0,2×2+m×(?2)+k×(?1)=0,解得m=2.
故答案为2.
14.【答案】?16
【解答】
解:因为直线l的一个方向向量d=(2,3,5),平面α的一个法向量u=(?4,m,n),l⊥α,则有d=(2,3,5)和u=(?4,m,n)平行,故有?42=m3=n5,解之得m=?6,n=?10,则m+n=?16.故答案为?16.
15.【答案】4
【解答】
解:因为α?//β,所以u//v,
即1?2=2?4=?2m,
解得m=4.
故答案为4.
16.【答案】x?y+2z+1=0
【解答】
解:由题意知AP⊥n,
所以AP·n=0,
因为AP=x,y?3,z?1,n=(1,?1,2),
所以x?y?3+2z?1=0,
即x?y+2z+1=0.
故答案为x?y+2z+1=0.
17.【答案】证明:以C为坐标原点,CB所在直线为x轴,CD所在直线为y轴,CP所在直线为z轴,建立如图所示的空间直角坐标系Cxyz.
∵PC⊥平面ABCD,
∴∠PBC为PB与平面ABCD所成的角,
∴∠PBC=30°.
∵PC=2,∴BC=23,PB=4,
∴D(0,1,0),B(23,0,0),A(23,4,0),P(0,0,2),M,
∴DP=(0,?1,2),DA=(23,3,0),
CM=(32,0,32).
(1)方法一令n=(x,y,z)为平面PAD的法向量,则DP·n=0DA·n=0即?y+2z=0,23x+3y=0,∴z=12yx=?32y
令y=2,得n=(?3,2,1).
∵n·CM=?3×32+2×0+1×32=0,∴n⊥CM.
又CM?平面PAD,∴CM?//平面PAD.
方法二∵PD=(0,1,?2),PA=(23,4,?2).
令CM=xPD+yPA,
则32=23y0=x+4y,32=?2x?2y,解方程组得x=?1,y=14
∴CM=?PD+14PA.
由共面向量定理知CM与PD,PA共面,
又∵CM?平面PAD,
∴CM?//平面PAD.
(2)取AP的中点E,连接BE,
则E(3,2,1),BE=(?3,2,1).
∵PB=AB,∴BE⊥PA.
又∵BE·DA=(?3,2,1)·(23,3,0)=0,
∴BE⊥DA,∴BE⊥DA,又PA∩DA=A,
PA,DA?平面PAD,
∴BE⊥平面PAD,又∵BE?平面PAB,
∴平面PAB⊥平面PAD.
18.【答案】证明:以点D为原点,DA,DC,DD1分别为x轴、y轴、z轴,建立空间直角坐标系,
令正方体的棱长为2,则D(0,0,0),A1(2,0,2),B(2,2,0),B1(2,2,2),E(1,1,2),F(1,2,1),
(1)EF→=(0,1,?1),A1B→=(0,2,?2),
因为A1B→=2EF→,所以A1B→//EF→,
所以EF//A1B;
(2)设平面A1BD的一个法向量为m→=(x,y,z),
则A1B→·m→=0,DB→·m→=0,
即2y?2z=0,2x+2y=0,令x=1,则m=(1,?1,?1),
因为m→·EF→=0,
所以EF//平面A1BD;
(3)由(2),同理求出平面EFB1的一个法向量n=(1,?1,?1),
所以平面B1EF//平面A1BD.
19.【答案】解:以A为原点,AB,AD,AA1?的方向分别为x轴,y轴,z轴的正方向建立如图所示的空间直角坐标系,设AB=a.
(Ⅰ)证明:A(0,0,0),D(0,1,0),D1(0,1,1),Ea2,1,0,B1(a,0,1),
故AD1=(0,1,1),B1E=?a2,1,?1,
因为B1E·AD1=?a2×0+1×1+(?1)×1=0,所以B1E⊥AD1.
(Ⅱ)假设在棱AA1上存在一点P(0,0,z0),使得DP//平面B1AE,
此时DP=(0,?1,z0),
再设平面B1AE的一个法向量为n=(x,y,z),
AB1=(a,0,1),AE=a2,1,0.
因为n⊥平面B1AE,
所以n⊥AB1,n⊥AE,即ax+z=0,ax2+y=0,
取x=1,得y=?a2,z=?a,得平面B1AE的一个法向量n=1,?a2,?a.
要使DP//平面B1AE,只要n⊥DP,有a2?az0=0,解得z0=12.
又DP?平面B1AE,所以存在点P,满足DP//平面B1AE,此时AP=12.
20.【答案】解:(1)如图,以A为坐标原点,射线AB、AD、AP分别为x轴、y轴、z轴正半轴,建立空间直角坐标系A?xyz.
设D(0,a,0),则B(6,0,0),C(6,a,0),P(0,0,6),E(62,0,62).
因此,AE=(62,0,62),BC=(0,a,0),PC=(6,a,?6).
则AE?BC=0,AE?PC=0,
所以AE⊥BC,AE⊥PC,又BC∩PC=C,所以AE⊥平面PBC.
由AD//BC,AD?平面PBC,BC?平面PBC,所以AD//平面PBC.
故直线AD与平面PBC的距离为点A到平面PBC的距离,即为|AE|=3.
(2)设平面AEC的法向量为n1=(x1,y1,z1).
因为AE=(62,0,62),AC=(6,3,0).
所以62x1+62z1=06x1+3y1=0,令x1=?1,得y1=2,z1=1,所以n1=(?1,2,1).
设平面EDC的法向量为n2=(x2,y2?z2),
因为EC=(62,3,?62),CD=(?6,0,0),
所以62x2+3y2?62z2=0?6x2=0,令z2=2,得y2=1,所以n2=(0,1,2).
由图可知二面角A?EC?D的平面角为一锐角,
所以二面角A?EC?D的平面角θ的余弦值为:cosθ=n1·n2n1·n2=222×3=63.
