1.4.2 用空间向量研究距离、夹角问题-【新教材】人教A版(2019)高中数学选择性必修第一册同步练习(Word含答案解析)
文档属性
| 名称 | 1.4.2 用空间向量研究距离、夹角问题-【新教材】人教A版(2019)高中数学选择性必修第一册同步练习(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 391.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 22:30:18 | ||
图片预览



文档简介
用空间向量研究距离、夹角问题同步练习
一、选择题
已知空间中三点A(1,0,0),B(2,1,?1),C(0,?1,2),则点C到直线AB的距离为(? ?).
A. 63 B. 62 C. 33 D. 32
如图,在三棱柱ABC?A1B1C1中,AA1⊥底面ABC,AA1=3,AB=AC=BC=2,则AA1与平面AB1C1所成角的大小为( )
A. 30°
B. 45°
C. 60°
D. 90°
已知平面α的一个法向量为n=(2,2,1),点A(?1,3,0)在平面α内,则点P(2,1,3)到平面α的距离为( )
A. 53 B. 43 C. 1 D. 23
在棱长均为23的正四面体ABCD中,M为AC的中点,E为AB的中点,P是DM上的动点,Q是平面ECD上的动点,则AP+PQ的最小值是( )
A. 3+112 B. 3+2 C. 543 D. 23
四棱锥P?ABCD中,AB=2?1,3,AD=?2,1,0,AP=3,?1,4,则这个四棱锥的高为(??? )
A. 55 B. 15 C. 25 D. 255
如图,正方体ABCD?A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F//平面AD1E,则A1F与平面BCC1B1所成角的正切值t构成的集合是( )
A. {t|255≤t≤233} B. {t|2≤t<22}
C. {t|255≤t≤23} D. {t|2≤t≤22}
在棱长为2的正方体ABCD?A1B1C1D1中,E,F分别为棱AA1、BB1的中点,M为棱A1B1上的一点,且A1M=λ(0<λ<2),设点N为ME的中点,则点N到平面D1EF的距离为( )
A. 3λ B. 22 C. 2λ3 D. 55
长方体ABCD?A1B1C1D1中,AB=AD=1,AAl=2,E为棱AA1的中点,则直线C1E与平面CB1D1所成角的余弦值为??? (??? )
A. 69 B. 539 C. 53 D. 23
在三棱锥P?ABC中,PC⊥底面ABC,∠BAC=90°,AB=AC=4,∠PBC=60°,则点C到平面PAB的距离是( )
A. 3427 B. 4427 C. 5427 D. 6427
已知平面α的一个法向量n=?2,?2,1,点A(?1,3,0)在平面α内,则P(?2,1,4)到α的距离为( )
A. 10 B. 3 C. 83 D. 103
在长方体ABCD?A1B1C1D1中,AD=7,AB=10,AA1=1,过点B作直线l与直线A1D及直线AC1所成的角均为π3,这样的直线l的条数为(??? )
A. 1 B. 2 C. 3 D. 4
已知四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2,将△ADC沿AC折起,使D到D′的位置,当D′B=10时,异面直线AB与直线CD′所成角的正切值为(? ?)
A. 78 B. 158 C. 157 D. 87
二、填空题
如图,在正四棱柱ABCD?A1B1C1D1中,底面边长为2,直线CC1与平面ACD1所成角的正弦值为13,则正四棱柱的高为______.
如图,在长方体ABCD?A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.若二面角D1?EC?D的大小为π4,则AE=__________.
在矩形ABCD中,AB=1,AD=2,△ABD沿对角线BD翻折,形成三棱锥A?BCD.
①当AC=3时,三棱锥A?BCD的体积为13;
②当面ABD⊥面BCD时,AB⊥CD;
③三棱锥A?BCD外接球的表面积为定值.
以上命题正确的是______.
已知正方体ABCD?A1B1C1D1的棱长为6,点M是对角线A1C上靠近点A1的三等分点,则三棱锥C?MBD的体积为______.
在棱长为1的正方体ABCD?A1B1C1D1中,E为CC1的中点,P,Q是正方体表面上相异两点,满足BP⊥A1E,BQ⊥A1E.
(1)若P,Q均在平面A1B1C1D1内,则PQ与BD的位置关系是______;
(2)|A1P|的最小值为______.
三、解答题
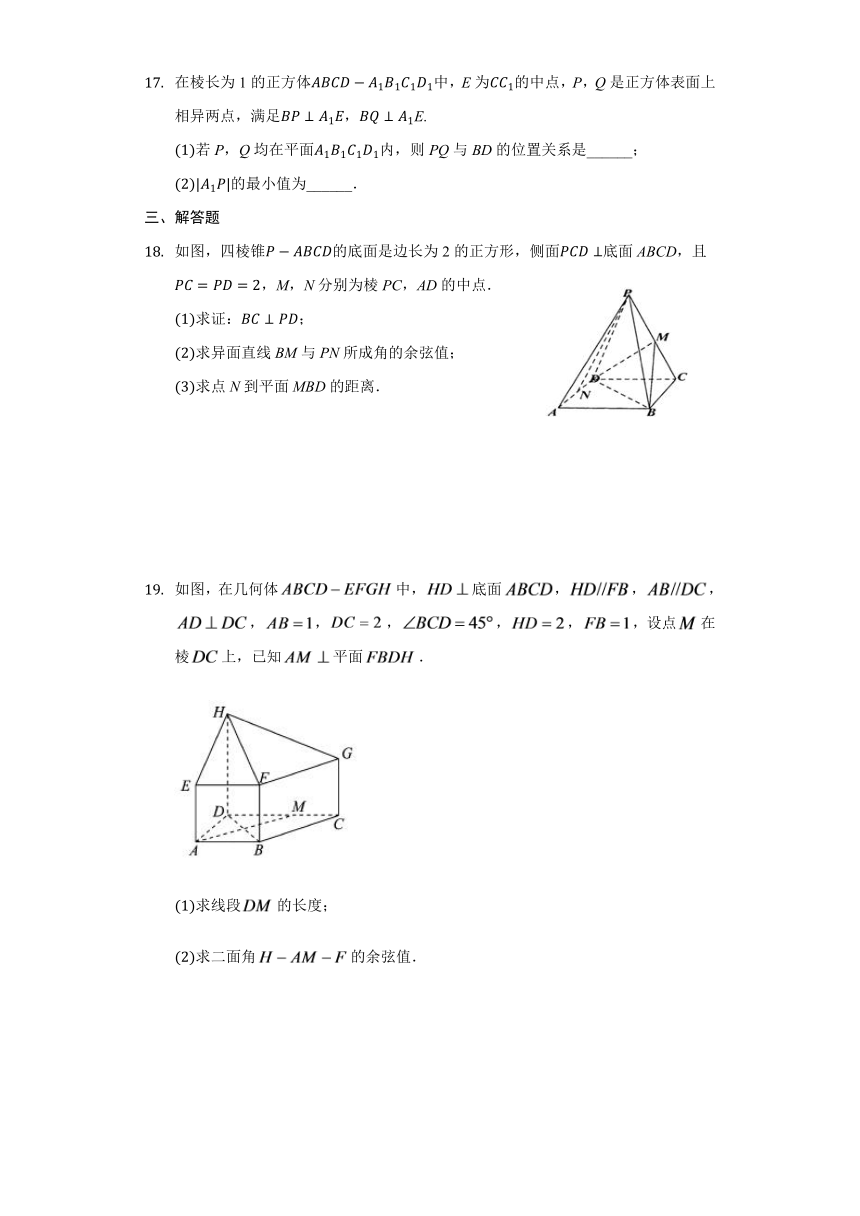
3530600470535如图,四棱锥P?ABCD的底面是边长为2的正方形,侧面PCD⊥底面ABCD,且PC=PD=2,M,N分别为棱PC,AD的中点.
(1)求证:BC⊥PD;
(2)求异面直线BM与PN所成角的余弦值;
(3)求点N到平面MBD的距离.
如图,在几何体中,底面,,,,,,,,,设点在棱上,已知平面.
(1)求线段的长度;
(2)求二面角的余弦值.
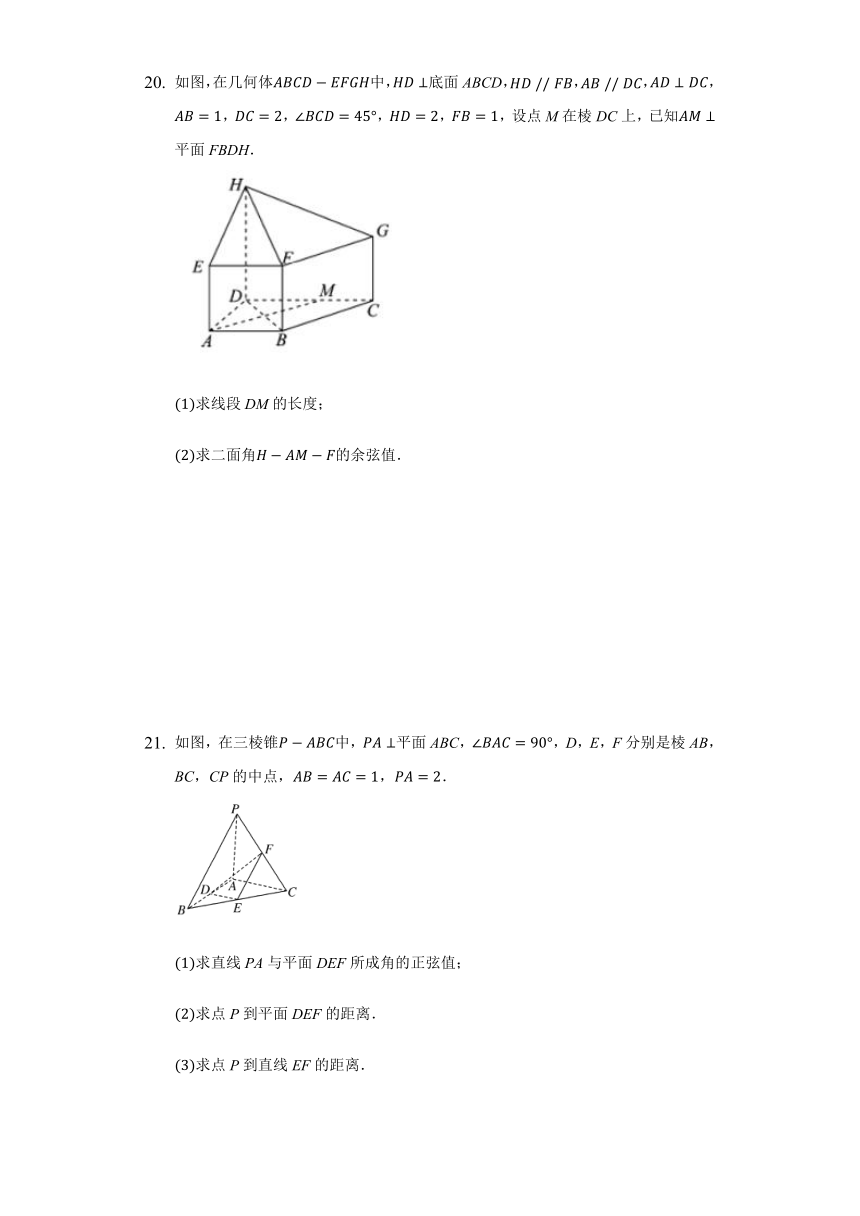
如图,在几何体ABCD?EFGH中,HD⊥底面ABCD,HD?//?FB,AB?//?DC,AD⊥DC,AB=1,DC=2,∠BCD=45°,HD=2,FB=1,设点M在棱DC上,已知AM⊥平面FBDH.
(1)求线段DM的长度;
(2)求二面角H?AM?F的余弦值.
如图,在三棱锥P?ABC中,PA⊥平面ABC,∠BAC=90°,D,E,F分别是棱AB,BC,CP的中点,AB=AC=1,PA=2.
(1)求直线PA与平面DEF所成角的正弦值;
(2)求点P到平面DEF的距离.
(3)求点P到直线EF的距离.
答案和解析
1.【答案】A
【解答】
解:由题意,可得AB=(1,1,?1),AC=(?1,?1,2),
cos,
∴sin=13,
所以点C到直线AB的距离
d=|AC|·sin=63.
故选A.
2.【答案】A
【解答】
解:以B为原点,在平面ABC中,过B作BC的垂线为x轴,以BC所在直线为y轴,BB1所在直线为z轴,建立如图所示的空间直角坐标系,
A(3,1,0),A1(3,1,3),B1(0,0,3),C1(0,2,3),
AA1=(0,0,3),B1C1=(0,2,0),B1A=(3,1,?3),
设平面AB1C1的法向量n=(x,y,z),
则n?B1C1=2y=0n?B1A=3x+y?3z=0,
取z=1,得n=(3,0,1),
设AA1与平面AB1C1所成角的大小为θ,
则.
∵0°≤θ≤90°,∴θ=30°.
∴AA1与平面AB1C1所成角的大小为30°.
故选:A.
3.【答案】A
【解析】解:∵面α的一个法向量为n=(2,2,1),
点A(?1,3,0)在平面α内,点P(2,1,3),
∴AP=(3,?2,3),
∴点P(2,1,3)到平面α的距离为:
d=|AP?n||n|=53.
4.【答案】A
【解析】解:由题意,平面CDE⊥平面ABC,
又平面CDE∩平面ABC=CE,过M作MG⊥CE,
则MG⊥平面CDE,连接DG,则DG为DM在平面CDE上的射影,
要使AP+PQ最小,则PQ⊥DG,沿DM把平面ADM展开,使得平面ADM与平面DMG重合,
则AP+PQ的最小值为A到DG的距离.
MG=12AE=32,DM=(23)2?(3)2=3,则sin∠MDG=36,
∴cos∠MDG=336,
∠ADM=30°,
∴sin∠ADG=sin(∠MDG+30°)=sin∠MDG?cos30°+cos∠MDG?sin30°
=36×32+336×12=3+3312.
又AD=23,∴AQ=23×3+3312=11+32.
5.【答案】A
【解答】
解:∵设面ABCD的法向量为n=x,y,z,
∴n·AB=0n·AD=0,
∴2x?y+3z=0?2x+y=0,
∵令x=1,则y=2,z=0,
∴n=1,2,0,
∵设n与AP的夹角为θ,设四棱锥的高为h,
∴cosθ=n·APn·AP=?AP,
∴?=n·APn=15=55,
故选A.
6.【答案】D
【解答】
解:?建立如下图所示的空间坐标系,
由A(1,0,0),D1(0,0,1),E(12,1,0),
由已知设F(a,1,b),
所以AD1=(?1,0,1),AE=(?12,1,0),AF=(a?1,1,b?1),
设平面AD1E的法向量为n→=(x,y,z),
由已知有AD1→·n→=?x+z=0AE→·n→=?12x+y=0,
令x=2,则n→=(2,1,2),
所以由A1F//平面AD1E得n·A1F=2(a?1)+1+2(b?1)=0,
即a+b=32,
所以|A1F|=(a?1)2+(b?1)2+1,
因为平面BCC1B1的法向量为m→=(0,1,0),
所以A1F与平面BCC1B1所成角的正弦值,
正切值,
令u=2a2?3a+54,
则umin=18,umax=12,
所以2?t?22.
故选D.
7.【答案】D
【解答】
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则E(2,0,1),M(2,λ,2),N2,λ2,32,D1(0,0,2),F(2,2,1),
∴EF=(0,2,0),ED1=(?2,0,1),EN=(0,λ2,12),
设平面D1EF的法向量为n=x,y,z,
则n·EF=0n·ED1=0,取x=1,得n=1,0,2,
∴点N到平面D1EF的距离为d=n·ENn=15=55.
故选D.
8.【答案】A
【解答】
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则D(0,0,0),C(0,1,0),D1(0,0,2),E(1,0,1),C1(0,1,2),B1(1,1,2),
∴C1E=(1,?1,?1),CB1=(1,0,2),D1B1=(1,1,0),
设平面CB1D1的法向量为n=(x,y,z),
则n?CB1=x+2z=0n?D1B1=x+y=0,
取z=1,得n=(?2,2,1),
设直线C1E与平面CB1D1所成角的余弦值为θ,
则sinθ=|C1E?n||C1E|?|n|=53?9=527,
∴cosθ=1?sin2θ=1?(527)2=227=69,
∴异面直线C1E与平面CB1D1所成角的余弦值为69,
故选A.
9.【答案】B
【解析】
【分析】
本题考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
以A为原点,AB为x轴,AC为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能求出点C到平面PAB的距离.
【解答】
解:∵在三棱锥P?ABC中,PC⊥底面ABC,∠BAC=90°,AB=AC=4,∠PBC=60°,
∴以A为原点,AB为x轴,AC为y轴,
过A作平面ABC的垂线为z轴,建立空间直角坐标系,
则C(0,4,0),P(0,4,46),A(0,0,0),
B(4,0,0),
AC=(0,4,0),AB=(4,0,0),
AP=(0,4,46),
设平面PAB的法向量n=(x,y,z),
则n?AP=4y+46z=0n?AB=4x=0,
取z=1,得n=(0,?6,1),
∴点C到平面PAB的距离d=|AC?n||n|=467=4427.
故选:B.
10.【答案】D
【解答】
解:?∵A(?1,3,0),P(?2,1,4),
∴AP=?1,?2,4,
又∵平面α的一个法向量n=(?2,?2,1),点A在α内,
∴点P到α的距离为d=AP·nn=?1×?2+?2×?2+4×14+4+1=103.
故选D.
11.【答案】C
【解答】
解:以D为原点,DA,DC,DD1所在直线为x,y,z轴建立如图坐标系,
因AD=7,AB=10,AA1=1
则D(0,0,0),A1(7,0,1),A7,0,0,C1(0,10,1),
所以DA1=7,0,1,AC1=?7,10,1,
所以直线A1D及直线AC1所成的角余弦值为cos=?7+18×18=12,
所以直线A1D及直线AC1所成的角为π3,
设过点B的直线方向向量为n,∵=60°,∴要使n与DA1,AC1的夹角均为60°,当n,DA1,AC1共面时有一种情况,当n,DA1,AC1时有两种情况,
所以过点B可作3条直线与直线A1D及直线AC1所成的角均为π3,
故选C.
12.【答案】C
【解答】
解:因为四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2.
易知∠ACB=90°,AC=23,记AC的中点为E,则DE⊥AC,EC=3,DE=1.
翻折后,D′E⊥AC,EC=3,D′E=1.
设二面角D′?AC?B的大小为θ,因为D′B=10,
由D′B=D′E+EC+CB,两边平方得(10)2=12+(3)2+22?2×1×2cosθ,
得cosθ=?12,则二面角D′?AC?B的大小为120°.
从点D′向平面ABC作垂线,垂足为O,
以O为坐标原点建立空间直角坐标系O?xyz,如图所示,
则A(3,12,0),B(?3,52,0),C(?3,12,0),D′(0,0,32),
则AB=(?23,2,0),CD′=(3,?12,32),
则,
则
故.
故选C.
13.【答案】4
【解析】解:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
设DD1=a,则A(2,0,0),C(0,2,0),D1(0,0,a),故AC=(?2,2,0),AD1=(?2,0,a),CC1=(0,0,a),
设平面ACD1的一个法向量为n=(x,y,z),则n?AC=?2x+2y=0n?AD1=?2x+az=0,可取n=(1,1,2a),
故cos=n?CC1|n||CC1|=2a?4a2+2=22a2+4,
又直线CC1与平面ACD1所成角的正弦值为13,
∴22a2+4=13,解得a=4.
故答案为:4.
建立空间直角坐标系,设棱柱的高为a,求出平面ACD1的一个法向量n,令cos=13,求出a的值即可.
14.【答案】2?3
【解答】
解:以点D为坐标原点,分别以DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系,设AE=a.
则A1(1,0,1),D1(0,0,1),E(1,a,0),A(1,0,0),C(0,2,0).
∴CE=(1,a?2,0),
D1C=(0,2,?1),
DD1=(0,0,1).
设平面D1EC的法向量为
n→=(x,y,z),
由n⊥D1C,n⊥CE,
可得n→·D1C=0,n→·CE=0,
即2y?z=0x+a?2y=0,
令y=1,则z=2,x=2?a.
∴n→=(2?a,1,2).
∵DD1⊥平面ABCD,
∴可取DD1作为平面ABCD的法向量.
由题意可得,即22?a2+1+22=22,解得a=2±3.
其中2+3不符合题意,应舍去,∴a=2?3.
∴AE=2?3.
故答案为2?3.
15.【答案】③
【解析】解:∵在矩形ABCD中,AB=1,AD=2,
∴AC=BD=12+22=5,
△ABD沿对角线BD翻折,形成三棱锥A?BCD.
在①中,取BD中点O,连结AO,CO,则AO=CO=52,
当AC=3时,cos∠AOC=54+54?32×52×52=?15,
∴sin∠AOC=1?(?15)2=265,
∴点A到平面BCD的距离d=52sin∠AOC=52×265=305.
∴三棱锥A?BCD的体积为:
V=13×12×2×1×305=3015,故①错误;
在②中,当面ABD⊥面BCD时,过点A作AE⊥平面BCD,交BD于E,
则AE⊥CD,又CD与平面ABD不垂直,故AB与CD不垂直,故②错误;
在③中,∵OA=OB=OC=OD=52,
∴三棱锥A?BCD外接球的球心为O,半径为52,
∴三棱锥A?BCD外接球的表面积为定值.故③正确.
故答案为:③.
在①中,取BD中点O,连结AO,CO,则AO=CO=52,当AC=3时,cos∠AOC=?15,从而sin∠AOC=265,点A到平面BCD的距离d=52sin∠AOC=305.由此能求出三棱锥A?BCD的体积;在②中,过点A作AE⊥平面BCD,交BD于E,则AE⊥CD,又CD与平面ABD不垂直,故AB与CD不垂直;在③中,三棱锥A?BCD外接球的球心为O,半径为52,从而三棱锥A?BCD外接球的表面积为定值.
16.【答案】24
【解析】解:∵点M是对角线A1C上靠近点A1的三等分点,
∴M到底面的距离d=23AA1=4,
又S△BCD=12×6×6=18,
∴VC?MBD=VM?BCD=13×18×4=24.
故答案为:24.
17.【答案】平行;?324
【解析】解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A1(1,0,1),E(0,1,12),B(1,1,0),
∵P,Q均在平面A1B1C1D1内,∴设P(a,b,1),Q(m,n,1),
则A1E=(?1,1,?12),BP=(a?1,b?1,1),BQ=(m?1,n?1,1),
∵BP⊥A1E,BQ⊥A1E.
∴BP?A1E=?(a?1)+(b?1)?12=0BQ?A1E=?(m?1)+(n?1)?12=0,
解得b?a=12n?m=12,∴PQ//BD,即PQ与BD的位置关系是平行.
(2)当|A1P|取最小值时,P在平面A1B1C1D1内,
设P(a,b,1),由(1)得b=a+12,
∴|A1P|=(a?1)2+b2=(a?1)2+(a+12)2
=2a2?a+54=2(a?14)2+98,
∴当a=14,即P(14,34,1)时,|A1P|的最小值为324.
故答案为:平行;324.
18.【答案】(1)证明:由题可知,侧面PCD⊥底面ABCD,取DC中点O,
因为PC=PD=2,则PO⊥交线CD,所以PO⊥底面ABCD,
如图,过O平行于DA直线为x轴,以OC,OP所在直线分别为y轴和z轴建立空间直角坐标系,
则A(2,?1,0),B(2,1,0),C(0,1,0),
D(0,?1,0),P(0,0,3),N(1,?1,0),
BC=(?2,0,0),PD=(0,?1,?3),
则BC?PD=0,所以BC⊥PD;
(2)解:由(1)可得,M(0,12,32),
PN=(1,?1,?3),BM=(?2,?12,32)
设异面直线BM与PN所成角为θ,
则cosθ=|PN?BM|PN|?|BM||=|?2+12?32|5?5=35.
所以异面直线BM与PN所成角的余弦值为35;
(3)解:因为BD=(?2,?2,0),BM=(?2,?12,32).
设平面MBD的一个法向量为m=(x,y,z),
由m?BD=0m?BM=0,得?2x?2y=0?2x?12y+32z=0,取y=?1,得x=1,z=3.
所以m=(1,?1,3),又DN=(1,0,0),
所以点N到平面MBD的距离d=|m?DN||m|=15=55.
19.【答案】解:以D为坐标原点,射线DA,DC,DH为x,y,z轴的正半轴,建立如图所示的空间直角坐标系D?xyz,
由AB//DC,AD⊥DC,AB=1,DC=2,∠BCD=45°,易知AD=1,
则A(1,0,0),B(1,1,0),C(0,2,0),D(0,0,0),H(0,0,2),F(1,1,1),
(1)设M(0,t,0),因为AM⊥平面FBDH,所以AM⊥BD,
AM=(?1,t,0),BD=(?1,?1,0),AM?BD=1?t=0,解得t=1,
所以线段DM的长度为1,
(2)设n1=(x,y,z)是平面HAM的一个法向量,AH=(?1,0,2),MF=(1,0,1),
则n1·AM=0n1?AH=0,?x+y=0?x+2z=0,可取n1=(2,2,1),
同理,设n2=(u,v,w)是平面AMF的一个法向量,
则n2?AM=0n2·MF=0??u+v=0u+w=0,可取n2=(1,1,?1),
则cos=n1·n2n1n2=33,显然二面角H?AM?F为锐二面角,
所以二面角H?AM?F的余弦值为33.
20.【答案】解:以D为坐标原点,射线DA为x轴的正半轴,建立如图所示的空间直角坐标系D?xyz,
由AB//DC,AD⊥DC,AB=1,DC=2,∠BCD=45°,易知AD=1.
则A(1,0,0),B(1,1,0),C(0,2,0),D(0,0,0),H(0,0,2),F(1,1,1)
(1)设M(0,t,0),
因为AM⊥平面FBDH,BD?平面FBDH,,
所以AM⊥BD,
AM=(?1,t,0),BD=(?1,?1,0),AM?BD=1?t=0,
解得t=1,所以线段DM的长度为1.
(2)设n1=(x,y,z)是平面HAM的一个法向量,
AH=(?1,0,2),MF=(1,0,1),
则n1?AM=0n1?MF=0??x+y=0?x+2z=0或取n1=(2,2,1),
同理,设n2=(u,ν,w)是平面AMF的一个法向量,
则n2?AM=0n2?MF=0??u+ν=0u+w=0,可取n2=(1,1,?1),
则cos??n1,n2?=n1?n2|n1||n2|=33,
显然二面角H?AM?F为锐二面角,
所以二面角H?AM?F的余弦值为33.
21.【答案】解:(1)如图所示,
以A为原点,AB,AC,AP所在的直线分别为x,y,z轴,建立空间直角坐标系A?xyz.
由AB=AC=1,PA=2,得A(0,0,0),B(1,0,0),C(0,1,0),P(0,0,2),D12,0,0,E12,12,0,F0,12,1.
设平面DEF的法向量n=(x,y,z),
则n·DE=0,n·DF=0,即(x,y,z)·0,12,0=0,(x,y,z)·?12,12,1=0,
解得x=2z,y=0.
取z=1,则平面DEF的一个法向量n=(2,0,1).
设PA与平面DEF所成的角为θ,
则sin?θ=|PA·n||PA|·|n|=55,
故直线PA与平面DEF所成角的正弦值为55.
(2)∵PF=0,12,?1,n=(2,0,1),
∴点P到平面DEF的距离d=|PF·n||n|=55.
(3)∵PF=0,12,?1,EF=?12,0,1,
点P在EF上的投影为|PF·EF||EF|=255,
所以点P到直线EF的距离为PF2?(255)2=1+14?45=920=4510.
一、选择题
已知空间中三点A(1,0,0),B(2,1,?1),C(0,?1,2),则点C到直线AB的距离为(? ?).
A. 63 B. 62 C. 33 D. 32
如图,在三棱柱ABC?A1B1C1中,AA1⊥底面ABC,AA1=3,AB=AC=BC=2,则AA1与平面AB1C1所成角的大小为( )
A. 30°
B. 45°
C. 60°
D. 90°
已知平面α的一个法向量为n=(2,2,1),点A(?1,3,0)在平面α内,则点P(2,1,3)到平面α的距离为( )
A. 53 B. 43 C. 1 D. 23
在棱长均为23的正四面体ABCD中,M为AC的中点,E为AB的中点,P是DM上的动点,Q是平面ECD上的动点,则AP+PQ的最小值是( )
A. 3+112 B. 3+2 C. 543 D. 23
四棱锥P?ABCD中,AB=2?1,3,AD=?2,1,0,AP=3,?1,4,则这个四棱锥的高为(??? )
A. 55 B. 15 C. 25 D. 255
如图,正方体ABCD?A1B1C1D1中,E是棱BC的中点,F是侧面BCC1B1上的动点,且A1F//平面AD1E,则A1F与平面BCC1B1所成角的正切值t构成的集合是( )
A. {t|255≤t≤233} B. {t|2≤t<22}
C. {t|255≤t≤23} D. {t|2≤t≤22}
在棱长为2的正方体ABCD?A1B1C1D1中,E,F分别为棱AA1、BB1的中点,M为棱A1B1上的一点,且A1M=λ(0<λ<2),设点N为ME的中点,则点N到平面D1EF的距离为( )
A. 3λ B. 22 C. 2λ3 D. 55
长方体ABCD?A1B1C1D1中,AB=AD=1,AAl=2,E为棱AA1的中点,则直线C1E与平面CB1D1所成角的余弦值为??? (??? )
A. 69 B. 539 C. 53 D. 23
在三棱锥P?ABC中,PC⊥底面ABC,∠BAC=90°,AB=AC=4,∠PBC=60°,则点C到平面PAB的距离是( )
A. 3427 B. 4427 C. 5427 D. 6427
已知平面α的一个法向量n=?2,?2,1,点A(?1,3,0)在平面α内,则P(?2,1,4)到α的距离为( )
A. 10 B. 3 C. 83 D. 103
在长方体ABCD?A1B1C1D1中,AD=7,AB=10,AA1=1,过点B作直线l与直线A1D及直线AC1所成的角均为π3,这样的直线l的条数为(??? )
A. 1 B. 2 C. 3 D. 4
已知四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2,将△ADC沿AC折起,使D到D′的位置,当D′B=10时,异面直线AB与直线CD′所成角的正切值为(? ?)
A. 78 B. 158 C. 157 D. 87
二、填空题
如图,在正四棱柱ABCD?A1B1C1D1中,底面边长为2,直线CC1与平面ACD1所成角的正弦值为13,则正四棱柱的高为______.
如图,在长方体ABCD?A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上.若二面角D1?EC?D的大小为π4,则AE=__________.
在矩形ABCD中,AB=1,AD=2,△ABD沿对角线BD翻折,形成三棱锥A?BCD.
①当AC=3时,三棱锥A?BCD的体积为13;
②当面ABD⊥面BCD时,AB⊥CD;
③三棱锥A?BCD外接球的表面积为定值.
以上命题正确的是______.
已知正方体ABCD?A1B1C1D1的棱长为6,点M是对角线A1C上靠近点A1的三等分点,则三棱锥C?MBD的体积为______.
在棱长为1的正方体ABCD?A1B1C1D1中,E为CC1的中点,P,Q是正方体表面上相异两点,满足BP⊥A1E,BQ⊥A1E.
(1)若P,Q均在平面A1B1C1D1内,则PQ与BD的位置关系是______;
(2)|A1P|的最小值为______.
三、解答题
3530600470535如图,四棱锥P?ABCD的底面是边长为2的正方形,侧面PCD⊥底面ABCD,且PC=PD=2,M,N分别为棱PC,AD的中点.
(1)求证:BC⊥PD;
(2)求异面直线BM与PN所成角的余弦值;
(3)求点N到平面MBD的距离.
如图,在几何体中,底面,,,,,,,,,设点在棱上,已知平面.
(1)求线段的长度;
(2)求二面角的余弦值.
如图,在几何体ABCD?EFGH中,HD⊥底面ABCD,HD?//?FB,AB?//?DC,AD⊥DC,AB=1,DC=2,∠BCD=45°,HD=2,FB=1,设点M在棱DC上,已知AM⊥平面FBDH.
(1)求线段DM的长度;
(2)求二面角H?AM?F的余弦值.
如图,在三棱锥P?ABC中,PA⊥平面ABC,∠BAC=90°,D,E,F分别是棱AB,BC,CP的中点,AB=AC=1,PA=2.
(1)求直线PA与平面DEF所成角的正弦值;
(2)求点P到平面DEF的距离.
(3)求点P到直线EF的距离.
答案和解析
1.【答案】A
【解答】
解:由题意,可得AB=(1,1,?1),AC=(?1,?1,2),
cos
∴sin
所以点C到直线AB的距离
d=|AC|·sin
故选A.
2.【答案】A
【解答】
解:以B为原点,在平面ABC中,过B作BC的垂线为x轴,以BC所在直线为y轴,BB1所在直线为z轴,建立如图所示的空间直角坐标系,
A(3,1,0),A1(3,1,3),B1(0,0,3),C1(0,2,3),
AA1=(0,0,3),B1C1=(0,2,0),B1A=(3,1,?3),
设平面AB1C1的法向量n=(x,y,z),
则n?B1C1=2y=0n?B1A=3x+y?3z=0,
取z=1,得n=(3,0,1),
设AA1与平面AB1C1所成角的大小为θ,
则.
∵0°≤θ≤90°,∴θ=30°.
∴AA1与平面AB1C1所成角的大小为30°.
故选:A.
3.【答案】A
【解析】解:∵面α的一个法向量为n=(2,2,1),
点A(?1,3,0)在平面α内,点P(2,1,3),
∴AP=(3,?2,3),
∴点P(2,1,3)到平面α的距离为:
d=|AP?n||n|=53.
4.【答案】A
【解析】解:由题意,平面CDE⊥平面ABC,
又平面CDE∩平面ABC=CE,过M作MG⊥CE,
则MG⊥平面CDE,连接DG,则DG为DM在平面CDE上的射影,
要使AP+PQ最小,则PQ⊥DG,沿DM把平面ADM展开,使得平面ADM与平面DMG重合,
则AP+PQ的最小值为A到DG的距离.
MG=12AE=32,DM=(23)2?(3)2=3,则sin∠MDG=36,
∴cos∠MDG=336,
∠ADM=30°,
∴sin∠ADG=sin(∠MDG+30°)=sin∠MDG?cos30°+cos∠MDG?sin30°
=36×32+336×12=3+3312.
又AD=23,∴AQ=23×3+3312=11+32.
5.【答案】A
【解答】
解:∵设面ABCD的法向量为n=x,y,z,
∴n·AB=0n·AD=0,
∴2x?y+3z=0?2x+y=0,
∵令x=1,则y=2,z=0,
∴n=1,2,0,
∵设n与AP的夹角为θ,设四棱锥的高为h,
∴cosθ=n·APn·AP=?AP,
∴?=n·APn=15=55,
故选A.
6.【答案】D
【解答】
解:?建立如下图所示的空间坐标系,
由A(1,0,0),D1(0,0,1),E(12,1,0),
由已知设F(a,1,b),
所以AD1=(?1,0,1),AE=(?12,1,0),AF=(a?1,1,b?1),
设平面AD1E的法向量为n→=(x,y,z),
由已知有AD1→·n→=?x+z=0AE→·n→=?12x+y=0,
令x=2,则n→=(2,1,2),
所以由A1F//平面AD1E得n·A1F=2(a?1)+1+2(b?1)=0,
即a+b=32,
所以|A1F|=(a?1)2+(b?1)2+1,
因为平面BCC1B1的法向量为m→=(0,1,0),
所以A1F与平面BCC1B1所成角的正弦值,
正切值,
令u=2a2?3a+54,
则umin=18,umax=12,
所以2?t?22.
故选D.
7.【答案】D
【解答】
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则E(2,0,1),M(2,λ,2),N2,λ2,32,D1(0,0,2),F(2,2,1),
∴EF=(0,2,0),ED1=(?2,0,1),EN=(0,λ2,12),
设平面D1EF的法向量为n=x,y,z,
则n·EF=0n·ED1=0,取x=1,得n=1,0,2,
∴点N到平面D1EF的距离为d=n·ENn=15=55.
故选D.
8.【答案】A
【解答】
解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则D(0,0,0),C(0,1,0),D1(0,0,2),E(1,0,1),C1(0,1,2),B1(1,1,2),
∴C1E=(1,?1,?1),CB1=(1,0,2),D1B1=(1,1,0),
设平面CB1D1的法向量为n=(x,y,z),
则n?CB1=x+2z=0n?D1B1=x+y=0,
取z=1,得n=(?2,2,1),
设直线C1E与平面CB1D1所成角的余弦值为θ,
则sinθ=|C1E?n||C1E|?|n|=53?9=527,
∴cosθ=1?sin2θ=1?(527)2=227=69,
∴异面直线C1E与平面CB1D1所成角的余弦值为69,
故选A.
9.【答案】B
【解析】
【分析】
本题考查点到平面的距离的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,是中档题.
以A为原点,AB为x轴,AC为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能求出点C到平面PAB的距离.
【解答】
解:∵在三棱锥P?ABC中,PC⊥底面ABC,∠BAC=90°,AB=AC=4,∠PBC=60°,
∴以A为原点,AB为x轴,AC为y轴,
过A作平面ABC的垂线为z轴,建立空间直角坐标系,
则C(0,4,0),P(0,4,46),A(0,0,0),
B(4,0,0),
AC=(0,4,0),AB=(4,0,0),
AP=(0,4,46),
设平面PAB的法向量n=(x,y,z),
则n?AP=4y+46z=0n?AB=4x=0,
取z=1,得n=(0,?6,1),
∴点C到平面PAB的距离d=|AC?n||n|=467=4427.
故选:B.
10.【答案】D
【解答】
解:?∵A(?1,3,0),P(?2,1,4),
∴AP=?1,?2,4,
又∵平面α的一个法向量n=(?2,?2,1),点A在α内,
∴点P到α的距离为d=AP·nn=?1×?2+?2×?2+4×14+4+1=103.
故选D.
11.【答案】C
【解答】
解:以D为原点,DA,DC,DD1所在直线为x,y,z轴建立如图坐标系,
因AD=7,AB=10,AA1=1
则D(0,0,0),A1(7,0,1),A7,0,0,C1(0,10,1),
所以DA1=7,0,1,AC1=?7,10,1,
所以直线A1D及直线AC1所成的角余弦值为cos
所以直线A1D及直线AC1所成的角为π3,
设过点B的直线方向向量为n,∵
所以过点B可作3条直线与直线A1D及直线AC1所成的角均为π3,
故选C.
12.【答案】C
【解答】
解:因为四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2.
易知∠ACB=90°,AC=23,记AC的中点为E,则DE⊥AC,EC=3,DE=1.
翻折后,D′E⊥AC,EC=3,D′E=1.
设二面角D′?AC?B的大小为θ,因为D′B=10,
由D′B=D′E+EC+CB,两边平方得(10)2=12+(3)2+22?2×1×2cosθ,
得cosθ=?12,则二面角D′?AC?B的大小为120°.
从点D′向平面ABC作垂线,垂足为O,
以O为坐标原点建立空间直角坐标系O?xyz,如图所示,
则A(3,12,0),B(?3,52,0),C(?3,12,0),D′(0,0,32),
则AB=(?23,2,0),CD′=(3,?12,32),
则,
则
故.
故选C.
13.【答案】4
【解析】解:以D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
设DD1=a,则A(2,0,0),C(0,2,0),D1(0,0,a),故AC=(?2,2,0),AD1=(?2,0,a),CC1=(0,0,a),
设平面ACD1的一个法向量为n=(x,y,z),则n?AC=?2x+2y=0n?AD1=?2x+az=0,可取n=(1,1,2a),
故cos
又直线CC1与平面ACD1所成角的正弦值为13,
∴22a2+4=13,解得a=4.
故答案为:4.
建立空间直角坐标系,设棱柱的高为a,求出平面ACD1的一个法向量n,令cos
14.【答案】2?3
【解答】
解:以点D为坐标原点,分别以DA、DC、DD1为x轴、y轴、z轴建立空间直角坐标系,设AE=a.
则A1(1,0,1),D1(0,0,1),E(1,a,0),A(1,0,0),C(0,2,0).
∴CE=(1,a?2,0),
D1C=(0,2,?1),
DD1=(0,0,1).
设平面D1EC的法向量为
n→=(x,y,z),
由n⊥D1C,n⊥CE,
可得n→·D1C=0,n→·CE=0,
即2y?z=0x+a?2y=0,
令y=1,则z=2,x=2?a.
∴n→=(2?a,1,2).
∵DD1⊥平面ABCD,
∴可取DD1作为平面ABCD的法向量.
由题意可得,即22?a2+1+22=22,解得a=2±3.
其中2+3不符合题意,应舍去,∴a=2?3.
∴AE=2?3.
故答案为2?3.
15.【答案】③
【解析】解:∵在矩形ABCD中,AB=1,AD=2,
∴AC=BD=12+22=5,
△ABD沿对角线BD翻折,形成三棱锥A?BCD.
在①中,取BD中点O,连结AO,CO,则AO=CO=52,
当AC=3时,cos∠AOC=54+54?32×52×52=?15,
∴sin∠AOC=1?(?15)2=265,
∴点A到平面BCD的距离d=52sin∠AOC=52×265=305.
∴三棱锥A?BCD的体积为:
V=13×12×2×1×305=3015,故①错误;
在②中,当面ABD⊥面BCD时,过点A作AE⊥平面BCD,交BD于E,
则AE⊥CD,又CD与平面ABD不垂直,故AB与CD不垂直,故②错误;
在③中,∵OA=OB=OC=OD=52,
∴三棱锥A?BCD外接球的球心为O,半径为52,
∴三棱锥A?BCD外接球的表面积为定值.故③正确.
故答案为:③.
在①中,取BD中点O,连结AO,CO,则AO=CO=52,当AC=3时,cos∠AOC=?15,从而sin∠AOC=265,点A到平面BCD的距离d=52sin∠AOC=305.由此能求出三棱锥A?BCD的体积;在②中,过点A作AE⊥平面BCD,交BD于E,则AE⊥CD,又CD与平面ABD不垂直,故AB与CD不垂直;在③中,三棱锥A?BCD外接球的球心为O,半径为52,从而三棱锥A?BCD外接球的表面积为定值.
16.【答案】24
【解析】解:∵点M是对角线A1C上靠近点A1的三等分点,
∴M到底面的距离d=23AA1=4,
又S△BCD=12×6×6=18,
∴VC?MBD=VM?BCD=13×18×4=24.
故答案为:24.
17.【答案】平行;?324
【解析】解:(1)以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A1(1,0,1),E(0,1,12),B(1,1,0),
∵P,Q均在平面A1B1C1D1内,∴设P(a,b,1),Q(m,n,1),
则A1E=(?1,1,?12),BP=(a?1,b?1,1),BQ=(m?1,n?1,1),
∵BP⊥A1E,BQ⊥A1E.
∴BP?A1E=?(a?1)+(b?1)?12=0BQ?A1E=?(m?1)+(n?1)?12=0,
解得b?a=12n?m=12,∴PQ//BD,即PQ与BD的位置关系是平行.
(2)当|A1P|取最小值时,P在平面A1B1C1D1内,
设P(a,b,1),由(1)得b=a+12,
∴|A1P|=(a?1)2+b2=(a?1)2+(a+12)2
=2a2?a+54=2(a?14)2+98,
∴当a=14,即P(14,34,1)时,|A1P|的最小值为324.
故答案为:平行;324.
18.【答案】(1)证明:由题可知,侧面PCD⊥底面ABCD,取DC中点O,
因为PC=PD=2,则PO⊥交线CD,所以PO⊥底面ABCD,
如图,过O平行于DA直线为x轴,以OC,OP所在直线分别为y轴和z轴建立空间直角坐标系,
则A(2,?1,0),B(2,1,0),C(0,1,0),
D(0,?1,0),P(0,0,3),N(1,?1,0),
BC=(?2,0,0),PD=(0,?1,?3),
则BC?PD=0,所以BC⊥PD;
(2)解:由(1)可得,M(0,12,32),
PN=(1,?1,?3),BM=(?2,?12,32)
设异面直线BM与PN所成角为θ,
则cosθ=|PN?BM|PN|?|BM||=|?2+12?32|5?5=35.
所以异面直线BM与PN所成角的余弦值为35;
(3)解:因为BD=(?2,?2,0),BM=(?2,?12,32).
设平面MBD的一个法向量为m=(x,y,z),
由m?BD=0m?BM=0,得?2x?2y=0?2x?12y+32z=0,取y=?1,得x=1,z=3.
所以m=(1,?1,3),又DN=(1,0,0),
所以点N到平面MBD的距离d=|m?DN||m|=15=55.
19.【答案】解:以D为坐标原点,射线DA,DC,DH为x,y,z轴的正半轴,建立如图所示的空间直角坐标系D?xyz,
由AB//DC,AD⊥DC,AB=1,DC=2,∠BCD=45°,易知AD=1,
则A(1,0,0),B(1,1,0),C(0,2,0),D(0,0,0),H(0,0,2),F(1,1,1),
(1)设M(0,t,0),因为AM⊥平面FBDH,所以AM⊥BD,
AM=(?1,t,0),BD=(?1,?1,0),AM?BD=1?t=0,解得t=1,
所以线段DM的长度为1,
(2)设n1=(x,y,z)是平面HAM的一个法向量,AH=(?1,0,2),MF=(1,0,1),
则n1·AM=0n1?AH=0,?x+y=0?x+2z=0,可取n1=(2,2,1),
同理,设n2=(u,v,w)是平面AMF的一个法向量,
则n2?AM=0n2·MF=0??u+v=0u+w=0,可取n2=(1,1,?1),
则cos
所以二面角H?AM?F的余弦值为33.
20.【答案】解:以D为坐标原点,射线DA为x轴的正半轴,建立如图所示的空间直角坐标系D?xyz,
由AB//DC,AD⊥DC,AB=1,DC=2,∠BCD=45°,易知AD=1.
则A(1,0,0),B(1,1,0),C(0,2,0),D(0,0,0),H(0,0,2),F(1,1,1)
(1)设M(0,t,0),
因为AM⊥平面FBDH,BD?平面FBDH,,
所以AM⊥BD,
AM=(?1,t,0),BD=(?1,?1,0),AM?BD=1?t=0,
解得t=1,所以线段DM的长度为1.
(2)设n1=(x,y,z)是平面HAM的一个法向量,
AH=(?1,0,2),MF=(1,0,1),
则n1?AM=0n1?MF=0??x+y=0?x+2z=0或取n1=(2,2,1),
同理,设n2=(u,ν,w)是平面AMF的一个法向量,
则n2?AM=0n2?MF=0??u+ν=0u+w=0,可取n2=(1,1,?1),
则cos??n1,n2?=n1?n2|n1||n2|=33,
显然二面角H?AM?F为锐二面角,
所以二面角H?AM?F的余弦值为33.
21.【答案】解:(1)如图所示,
以A为原点,AB,AC,AP所在的直线分别为x,y,z轴,建立空间直角坐标系A?xyz.
由AB=AC=1,PA=2,得A(0,0,0),B(1,0,0),C(0,1,0),P(0,0,2),D12,0,0,E12,12,0,F0,12,1.
设平面DEF的法向量n=(x,y,z),
则n·DE=0,n·DF=0,即(x,y,z)·0,12,0=0,(x,y,z)·?12,12,1=0,
解得x=2z,y=0.
取z=1,则平面DEF的一个法向量n=(2,0,1).
设PA与平面DEF所成的角为θ,
则sin?θ=|PA·n||PA|·|n|=55,
故直线PA与平面DEF所成角的正弦值为55.
(2)∵PF=0,12,?1,n=(2,0,1),
∴点P到平面DEF的距离d=|PF·n||n|=55.
(3)∵PF=0,12,?1,EF=?12,0,1,
点P在EF上的投影为|PF·EF||EF|=255,
所以点P到直线EF的距离为PF2?(255)2=1+14?45=920=4510.
