1.3集合的基本运算-【新教材】人教A版(2019)高中数学必修第一册课后练习(Word含答案)
文档属性
| 名称 | 1.3集合的基本运算-【新教材】人教A版(2019)高中数学必修第一册课后练习(Word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 117.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-09 22:49:37 | ||
图片预览


文档简介
2020-2021学年第一学期人教A版(2019)必修第一册1.3集合的基本运算课后练习
一、单选题
1.已知false,false,则false( )
A.false B.{0,1} C.{1,2} D.false
2.已知false,false,false,则下列运算中错误的是( )
A.false B.false
C.false D.false
3.我们知道,如果集合false,那么S的子集A的补集为false且false.类似地,对于集合false,我们把集合false,且false叫做集合A与B的差集,记作false.设false,若false,则差集false是( )
A.false B.false C.false D.false
4.设集合false,false,则false等于
A.false B.false C.false D.false
5.设集合A={1,2,3,4},B={3,4,5},全集U=A∪B,则集合?U(A∩B)的元素个数为( )
A.1个 B.2个 C.3个 D.4个
6.设集合false,false,集合false中所有元素之和为8,则实数false的取值集合为( )
A.falseB.false B.false C.false
7.设集合U={x|x<3},A={x|x<1},则CUA=( )
A.{x|1≤x<3} B.{x|1<x≤3} C.{x|1<x<3} D.{x|x≥1}
8.设集合S=|x|x<﹣1或x>5},T={x|a<x<a+8},且S∪T=R,则实数a的取值范围是( )
A.﹣3<a<﹣1 B.﹣3≤a≤﹣1
C.a≤﹣3或a≥﹣1 D.a<﹣3或a>﹣1
二、填空题
9.设集合false,集合false,且false,则a+b=_______.
10.已知集合false,false,若false则实数false的值为________
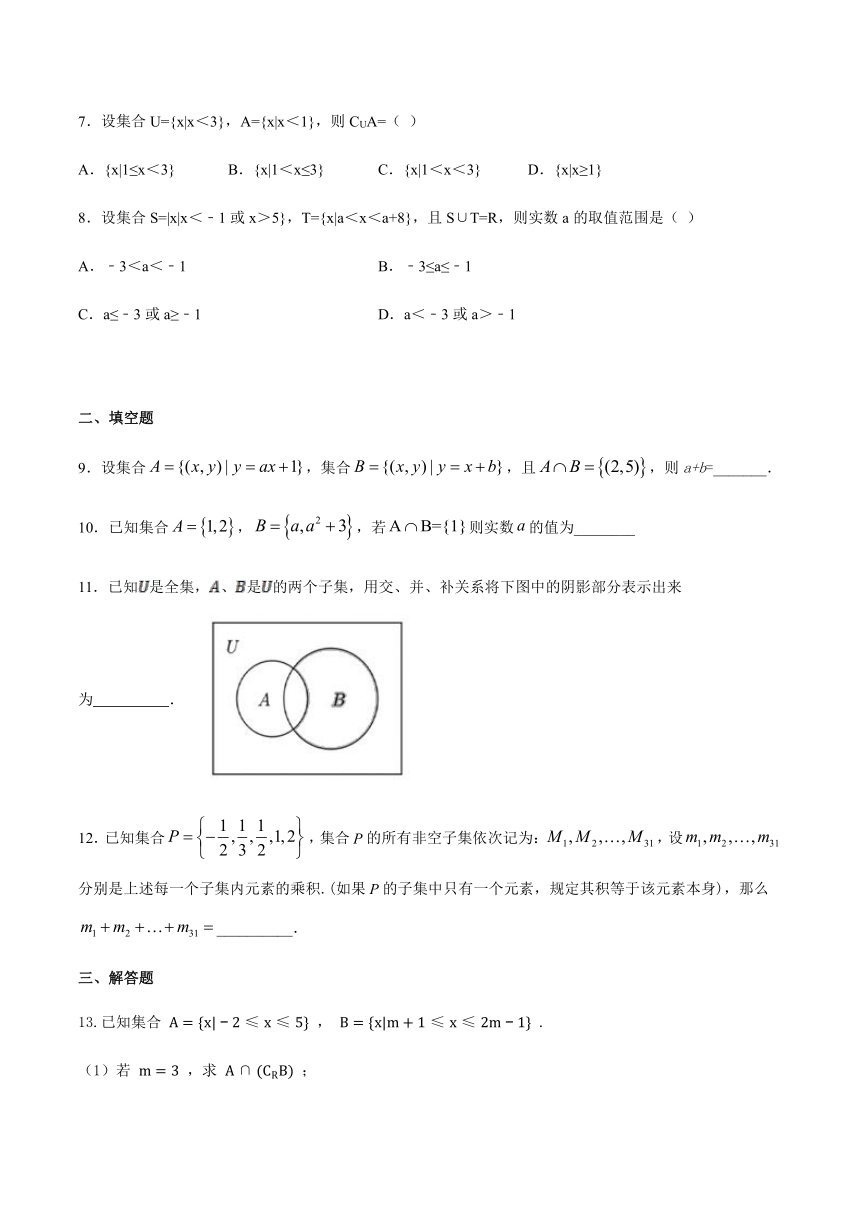
11.已知是全集,、是的两个子集,用交、并、补关系将下图中的阴影部分表示出来为 .
12.已知集合false,集合false的所有非空子集依次记为:false,设false分别是上述每一个子集内元素的乘积.(如果false的子集中只有一个元素,规定其积等于该元素本身),那么false__________.
三、解答题
13.已知集合 A={x|?2≤x≤5} , B={x|m+1≤x≤2m?1} .
(1)若 m=3 ,求 A∩(CRB) ;
(2)若 A∩B=B ,求实数 m 的取值范围.
14.已知p:实数x满足集合 A={x||x?a|≤1} ,q:实数x满足集合 B={x|x(1)若 a=?1 ,求 CR(A∪B) ;
(2)若p是q的充分不必要条件,求实数a的取值范围.
15.已知集合 A={x|(x?2a)?(x?a?3)<0} , B={1,2,3}
(1)若 a=1 ,求 A∩B ;
(2)若 a≠3 ,写出A对应的区间,并在 A∩B={1,2} 时,求a的取值范围.
16.不等式 x2?x?2>0 的解集为A,关于x的不等式 2x2+(5+2a)x+5a<0 的解集为B.
(1)求集合A、集合B;
(2)若集合 A∩B∩Z 中有2019个元素,求实数a的取值范围.
参考答案
D2.D3.C4.B5.C6.C7.A8.A9.510.111.12.5
13.【答案】 (1)解:当 m=3 时,可得 B={x|4≤x≤5}=[4,5] ,则 CRB=(?∞,4)∪(5,+∞) ;
所以 A∩(CRB)=[?2,4) .
(2)解:由 A∩B=B ,即 B?A ,
当 B=? 时,可得 m+1>2m?1 ,解得 m<2 ,此时满足 B?A ;
当 B≠? 时,要使得 B?A ,则满足 {m+1≤2m?1m+1≥?22m?1≤5 ,解得 2≤m≤3 .
综上可得,实数 m 的取值范围是 (?∞,3] .
【解析】(1)当 m=3 时,求得 B=[4,5] ,得到 CRB=(?∞,4)∪(5,+∞) ,在结合集合的交集运算,即可求解;(2)由 A∩B=B ,得到 B?A ,分 B=? 和 B≠? 两种情况分类讨论,即可求解.
14.【答案】 (1)解:当 a=?1 , |x?a|=|x+1|≤1 ,
所以 A={x|?2≤x≤0}
A∪B = {x|x≤0 或 x≥3}
CR(A∪B) ={x|0(2)解:集合 A={x||x?a|≤1}={a?1≤x≤a+1}
因为p是q的充分不必要条件
所以 a+1所以 a所以实数a的取值范围 (?∞,?3)∪[4,+∞) .
【解析】(1)算出集合 A ,以及 A∪B ,从而求出答案;(2)化简集合 A={x||x?a|≤1}={a?1≤x≤a+1} ,根据p是q的充分不必要条件,得到 a+115.【答案】 (1)解:由题意知: A={x|x2?6x+8<0}={x|2∴A∩B={3}
(2)解: ∵A={x|(x?2a)?[x?(a+3)]<0}
法一:当 a>3 时, A=(a+3,2a) , A∩B=? ,不合题意,
当 a<3 时, A=(2a,a+3) ,
所以, 1,2∈A,3?A ,即 2a<1,?????2∴a∈(?1,0] .
法二:当 a>3 时, A=(a+3,2a) ;当 a<3 时, A=(2a,a+3)
由 1,2∈A,3?A ,得 {(2a?1)(a+2)<0(2a?2)(a+1)<0a(2a?3)≥0 .
解得 a∈(?1,0]
【解析】(1)求解二次不等式再求交集即可.(2)由题意,分 a>3 和 a<3 两种情况进行讨论分析,再列出区间端点满足的关系式求解即可.
16.【答案】 (1)解: x2?x?2=(x?2)(x+1)>0 ,解得: x2
∴A=(?∞,?1)∪(2,+∞)
2x2+(5+2a)x+5a=(2x+5)(x+a)<0
当 ?a52 时, ?a当 ?a>?52 ,即 a<52 时, ?52∴B={(?a,?52),a>52?,a=52(?52,?a),a<52
(2)解:若 A∩B∩Z 有2019个元素,则 A∩B 中包含2019个整数
①当 a>52 时, ?a∴?a∈[?2022,?2021) ,即 a∈(2021,2022]
②当 1≤a<52 时, ?52则 A∩B 中不包含2019个整数,不合题意
③当 ?2≤a<1 ,即 ?1则 A∩B 中不包含2019个整数,不合题意
④当 a2 时, A∩B=(?52,?1)∪(2,?a)
∵(?52,?1) 包含 1 个整数??? ∴(2,?a) 需包含2018个整数
∴?a∈(2020,2021] ,即 a∈[?2021,?2020)
综上所述: a∈[?2021,2020)∪(2021,2022]
【解析】(1)利用一元二次不等式的解法可求得集合A;分别在 a>52 、 a<52 和 a=52 三种情况下,根据一元二次不等式解法求得集合B;(2)将问题转化为则 A∩B 中包含2019个整数;分别在 a>52 、 1≤a<52 、 ?2≤a<1 和 a
一、单选题
1.已知false,false,则false( )
A.false B.{0,1} C.{1,2} D.false
2.已知false,false,false,则下列运算中错误的是( )
A.false B.false
C.false D.false
3.我们知道,如果集合false,那么S的子集A的补集为false且false.类似地,对于集合false,我们把集合false,且false叫做集合A与B的差集,记作false.设false,若false,则差集false是( )
A.false B.false C.false D.false
4.设集合false,false,则false等于
A.false B.false C.false D.false
5.设集合A={1,2,3,4},B={3,4,5},全集U=A∪B,则集合?U(A∩B)的元素个数为( )
A.1个 B.2个 C.3个 D.4个
6.设集合false,false,集合false中所有元素之和为8,则实数false的取值集合为( )
A.falseB.false B.false C.false
7.设集合U={x|x<3},A={x|x<1},则CUA=( )
A.{x|1≤x<3} B.{x|1<x≤3} C.{x|1<x<3} D.{x|x≥1}
8.设集合S=|x|x<﹣1或x>5},T={x|a<x<a+8},且S∪T=R,则实数a的取值范围是( )
A.﹣3<a<﹣1 B.﹣3≤a≤﹣1
C.a≤﹣3或a≥﹣1 D.a<﹣3或a>﹣1
二、填空题
9.设集合false,集合false,且false,则a+b=_______.
10.已知集合false,false,若false则实数false的值为________
11.已知是全集,、是的两个子集,用交、并、补关系将下图中的阴影部分表示出来为 .
12.已知集合false,集合false的所有非空子集依次记为:false,设false分别是上述每一个子集内元素的乘积.(如果false的子集中只有一个元素,规定其积等于该元素本身),那么false__________.
三、解答题
13.已知集合 A={x|?2≤x≤5} , B={x|m+1≤x≤2m?1} .
(1)若 m=3 ,求 A∩(CRB) ;
(2)若 A∩B=B ,求实数 m 的取值范围.
14.已知p:实数x满足集合 A={x||x?a|≤1} ,q:实数x满足集合 B={x|x(1)若 a=?1 ,求 CR(A∪B) ;
(2)若p是q的充分不必要条件,求实数a的取值范围.
15.已知集合 A={x|(x?2a)?(x?a?3)<0} , B={1,2,3}
(1)若 a=1 ,求 A∩B ;
(2)若 a≠3 ,写出A对应的区间,并在 A∩B={1,2} 时,求a的取值范围.
16.不等式 x2?x?2>0 的解集为A,关于x的不等式 2x2+(5+2a)x+5a<0 的解集为B.
(1)求集合A、集合B;
(2)若集合 A∩B∩Z 中有2019个元素,求实数a的取值范围.
参考答案
D2.D3.C4.B5.C6.C7.A8.A9.510.111.12.5
13.【答案】 (1)解:当 m=3 时,可得 B={x|4≤x≤5}=[4,5] ,则 CRB=(?∞,4)∪(5,+∞) ;
所以 A∩(CRB)=[?2,4) .
(2)解:由 A∩B=B ,即 B?A ,
当 B=? 时,可得 m+1>2m?1 ,解得 m<2 ,此时满足 B?A ;
当 B≠? 时,要使得 B?A ,则满足 {m+1≤2m?1m+1≥?22m?1≤5 ,解得 2≤m≤3 .
综上可得,实数 m 的取值范围是 (?∞,3] .
【解析】(1)当 m=3 时,求得 B=[4,5] ,得到 CRB=(?∞,4)∪(5,+∞) ,在结合集合的交集运算,即可求解;(2)由 A∩B=B ,得到 B?A ,分 B=? 和 B≠? 两种情况分类讨论,即可求解.
14.【答案】 (1)解:当 a=?1 , |x?a|=|x+1|≤1 ,
所以 A={x|?2≤x≤0}
A∪B = {x|x≤0 或 x≥3}
CR(A∪B) ={x|0
因为p是q的充分不必要条件
所以 a+1所以 a所以实数a的取值范围 (?∞,?3)∪[4,+∞) .
【解析】(1)算出集合 A ,以及 A∪B ,从而求出答案;(2)化简集合 A={x||x?a|≤1}={a?1≤x≤a+1} ,根据p是q的充分不必要条件,得到 a+115.【答案】 (1)解:由题意知: A={x|x2?6x+8<0}={x|2
(2)解: ∵A={x|(x?2a)?[x?(a+3)]<0}
法一:当 a>3 时, A=(a+3,2a) , A∩B=? ,不合题意,
当 a<3 时, A=(2a,a+3) ,
所以, 1,2∈A,3?A ,即 2a<1,?????2
法二:当 a>3 时, A=(a+3,2a) ;当 a<3 时, A=(2a,a+3)
由 1,2∈A,3?A ,得 {(2a?1)(a+2)<0(2a?2)(a+1)<0a(2a?3)≥0 .
解得 a∈(?1,0]
【解析】(1)求解二次不等式再求交集即可.(2)由题意,分 a>3 和 a<3 两种情况进行讨论分析,再列出区间端点满足的关系式求解即可.
16.【答案】 (1)解: x2?x?2=(x?2)(x+1)>0 ,解得: x2
∴A=(?∞,?1)∪(2,+∞)
2x2+(5+2a)x+5a=(2x+5)(x+a)<0
当 ?a52 时, ?a
(2)解:若 A∩B∩Z 有2019个元素,则 A∩B 中包含2019个整数
①当 a>52 时, ?a∴?a∈[?2022,?2021) ,即 a∈(2021,2022]
②当 1≤a<52 时, ?52则 A∩B 中不包含2019个整数,不合题意
③当 ?2≤a<1 ,即 ?1则 A∩B 中不包含2019个整数,不合题意
④当 a2 时, A∩B=(?52,?1)∪(2,?a)
∵(?52,?1) 包含 1 个整数??? ∴(2,?a) 需包含2018个整数
∴?a∈(2020,2021] ,即 a∈[?2021,?2020)
综上所述: a∈[?2021,2020)∪(2021,2022]
【解析】(1)利用一元二次不等式的解法可求得集合A;分别在 a>52 、 a<52 和 a=52 三种情况下,根据一元二次不等式解法求得集合B;(2)将问题转化为则 A∩B 中包含2019个整数;分别在 a>52 、 1≤a<52 、 ?2≤a<1 和 a
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
