四年级下册数学课件-7.10 多边形的内角和苏教版(共31张PPT)
文档属性
| 名称 | 四年级下册数学课件-7.10 多边形的内角和苏教版(共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 16:04:00 | ||
图片预览




文档简介
(共31张PPT)
由这图形你抽象出什么几何图形?
三角形
观察
四边形
由这图形你抽象出什么几何图形?
观察
由这图形你抽象出什么几何图形?
五边形
观察
六边形
由这图形你抽象出什么几何图形?
观察
由这图形你抽象出什么几何图形?
八边形
观察
三角形的定义:
在同一平面内,三条线段首尾相接围成的图形叫做三角形。
在同一平面内,由不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形。
多边形的定义
……
五边形
六边形
七边形
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
内角:多边形相邻两边组成的角
对角线:链接多边形不相邻的两个顶点的线段
多边形的相关概念
钝角三角形
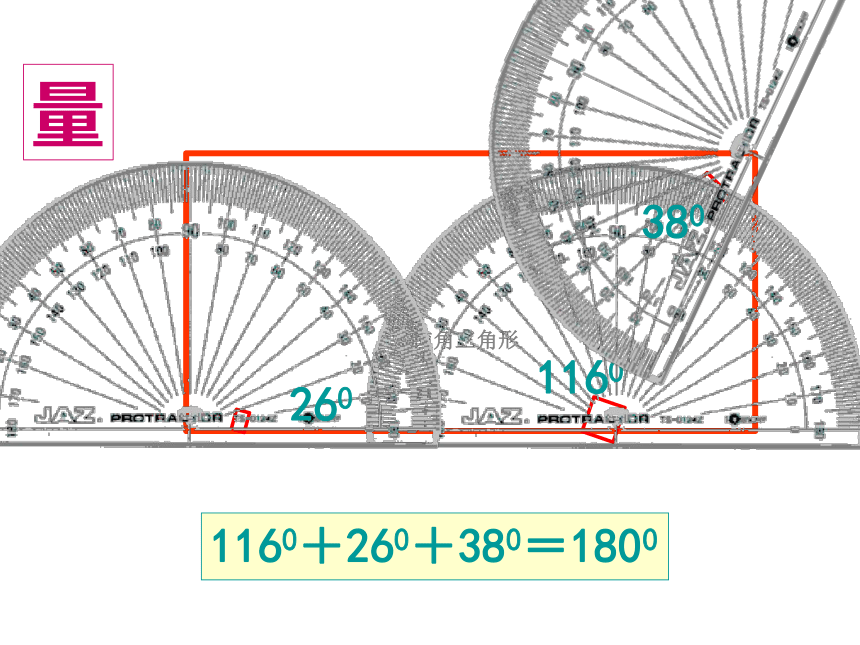
260
1160
1160+260+380=1800
380
量
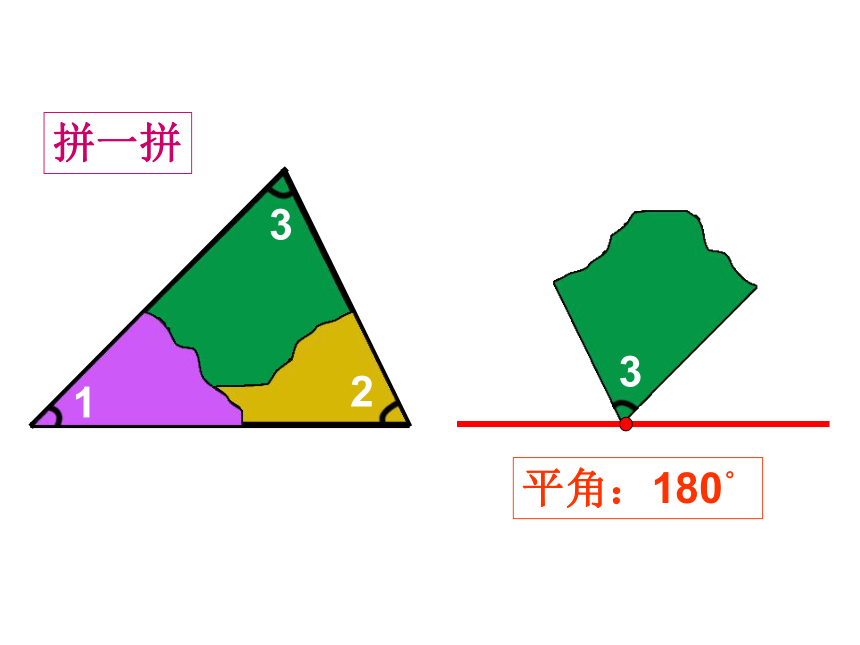
3
2
3
1
平角:180°
拼一拼
2
3
1
1
折一折
四边形
五边形
六边形
七边形
八边形
二十边形
三角形
180°
90°×4=360°
回忆 长方形、正方形的内角和等于______.
360°
创设情境,导入新知
思考 任意一个四边形的内角和是否也等于360°
呢?
这个四边形的内角和是多少度?
猜想:
探索研究方法。
1.拿出课前准备的四边形纸片,想办法求出这个四边形的4个内角的和。
2.将你的方法跟组内其他同学进行交流。
动手操作,探究新知
探究 你能利用三角形内角和定理证明你的结论
吗?
证明:连接AC,可以把四边形分成两个三角形:
180°
+
180°
=
360°
180°
×
2
=
360°
A
B
C
D
动手操作,探究新知
探究 你能利用三角形内角和定理证明你的结论
吗?
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
180°×2
1
2
3
4
5
6
1.把下面五边形、六边形分成若干个三角形,并算出它们的内角和。
2.组内交流你的分法。
探索分法。
五边形内角和=
六边形内角和=
180°×3
180°×4
A
B
C
D
E
动手操作,探究新知
探究 类比前面的过程,你能探索五边形的内角和
吗?六边形呢?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
动手操作,探究新知
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.
3
4
4
720
C
A
B
D
E
F
从n
边形的一个顶点出发,可以作对角线,它们将n
边形分为(n
-2)个三角形,这(n
-2)个三角形的内角和就是n
边形的内角和,所以,n
边形的内角和等于(n
-2)×180°.
归纳总结,获得新知
思考 你能从四边形、五边形、六边形的内角和的
研究过程获得启发,发现多边形的内角和与边数的关系
吗?能证明你发现的结论吗?
探寻规律。
1.
组内分工,每位组员研究一个图形,并把得到的结果填入下表中,组长负责汇总。
图形名称
边数
分成的三角形个数
内角和
三角形
3
1
180°
四边形
4
2
180°×2
五边形
5
六边形
七边形
八边形
……
……
……
……
2.
观察表中的数据,你有什么发现?
3.
组内交流你的发现。
3
180°×3
6
4
180°×4
7
8
5
6
180°×5
180°×6
4.
组内讨论:多边形的内角和=
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形
……
三角形
四边形
五边形
六边形
探究
n边形
……
三角形
四边形
五边形
六边形
1.十二边形的内角和是(
)。
2.内角和是2520°的多边形是(
)边形。
1800°
十六
由这图形你抽象出什么几何图形?
三角形
观察
四边形
由这图形你抽象出什么几何图形?
观察
由这图形你抽象出什么几何图形?
五边形
观察
六边形
由这图形你抽象出什么几何图形?
观察
由这图形你抽象出什么几何图形?
八边形
观察
三角形的定义:
在同一平面内,三条线段首尾相接围成的图形叫做三角形。
在同一平面内,由不在同一条直线上的一些线段首尾顺次相接组成的图形叫做多边形。
多边形的定义
……
五边形
六边形
七边形
多边形按组成它的线段条数分成三角形、四边形、五边形……其中三角形是最简单的多边形。
如果一个多边形由n条线段组成,那么这个多边形就叫做n边形。
内角:多边形相邻两边组成的角
对角线:链接多边形不相邻的两个顶点的线段
多边形的相关概念
钝角三角形
260
1160
1160+260+380=1800
380
量
3
2
3
1
平角:180°
拼一拼
2
3
1
1
折一折
四边形
五边形
六边形
七边形
八边形
二十边形
三角形
180°
90°×4=360°
回忆 长方形、正方形的内角和等于______.
360°
创设情境,导入新知
思考 任意一个四边形的内角和是否也等于360°
呢?
这个四边形的内角和是多少度?
猜想:
探索研究方法。
1.拿出课前准备的四边形纸片,想办法求出这个四边形的4个内角的和。
2.将你的方法跟组内其他同学进行交流。
动手操作,探究新知
探究 你能利用三角形内角和定理证明你的结论
吗?
证明:连接AC,可以把四边形分成两个三角形:
180°
+
180°
=
360°
180°
×
2
=
360°
A
B
C
D
动手操作,探究新知
探究 你能利用三角形内角和定理证明你的结论
吗?
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
180°×2
1
2
3
4
5
6
1.把下面五边形、六边形分成若干个三角形,并算出它们的内角和。
2.组内交流你的分法。
探索分法。
五边形内角和=
六边形内角和=
180°×3
180°×4
A
B
C
D
E
动手操作,探究新知
探究 类比前面的过程,你能探索五边形的内角和
吗?六边形呢?
如图,从五边形的一个顶点
出发,可以作 条对角线,它
们将五边形分为____个三角形,
五边形的内角和等于
180°× = °.
2
3
3
540
动手操作,探究新知
如图,从六边形的一个顶点出发,可以作_____条
对角线,它们将六边形分为_____个三角形,六边形的
内角和等于180°×____=_______°.
3
4
4
720
C
A
B
D
E
F
从n
边形的一个顶点出发,可以作对角线,它们将n
边形分为(n
-2)个三角形,这(n
-2)个三角形的内角和就是n
边形的内角和,所以,n
边形的内角和等于(n
-2)×180°.
归纳总结,获得新知
思考 你能从四边形、五边形、六边形的内角和的
研究过程获得启发,发现多边形的内角和与边数的关系
吗?能证明你发现的结论吗?
探寻规律。
1.
组内分工,每位组员研究一个图形,并把得到的结果填入下表中,组长负责汇总。
图形名称
边数
分成的三角形个数
内角和
三角形
3
1
180°
四边形
4
2
180°×2
五边形
5
六边形
七边形
八边形
……
……
……
……
2.
观察表中的数据,你有什么发现?
3.
组内交流你的发现。
3
180°×3
6
4
180°×4
7
8
5
6
180°×5
180°×6
4.
组内讨论:多边形的内角和=
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形
……
三角形
四边形
五边形
六边形
探究
n边形
……
三角形
四边形
五边形
六边形
1.十二边形的内角和是(
)。
2.内角和是2520°的多边形是(
)边形。
1800°
十六
