华师大版七年级上册地数学第3章 整式的加减3.4.1.2 同类项 合并同类项 课件(23张PPT)
文档属性
| 名称 | 华师大版七年级上册地数学第3章 整式的加减3.4.1.2 同类项 合并同类项 课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 542.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-11 17:24:15 | ||
图片预览








文档简介
华师大版 七年级 上册
03
同类项 合并同类项
情境导入
每个单项式叫做多项式的项.
找出 这个多项式的项:
3x2y-4xy2-3+5x2y+2xy2+5
3x2y,-4xy2, -3, 5x2y, 2xy2, 5
找找这些项中,有哪些具有相同的特征?
3x2y和5x2y
-4xy2和2xy2
-3和5
探索新知
3x2y和5x2y
4xy2和2xy2
3和5
所含字母相同,且x的指数都是2,y的指数都是1
所含字母相同,且x的指数都是1,y的指数都是2
都是常数项
像这样,所含字母相同,并且相同字母的指数也相等的项叫做同类项.所有常数项都是同类项.
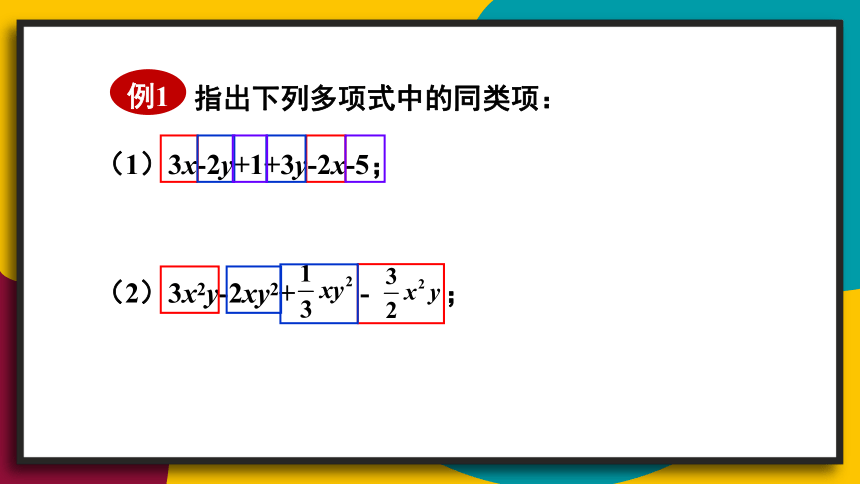
例1
指出下列多项式中的同类项:
(1)3x-2y+1+3y-2x-5;
(2)3x2y-2xy2+ - ;
例2
k取何值时,3xky与-x2y是同类项?
解 要使3xky与-x2y是同类项,那么这两项中的x的指数就必须相等,即k=2.
所以当k=2时, 3xky与-x2y是同类项.
如果一个多项式中含有同类项,那么我们可以把同类项合并起来,使结果得以简化.
将同类项3x2y和5x2y合并
3x2y+5x2y=(3+5)x2y =8x2y
对多项式 进行合并:
3x2y-4xy2-3+5x2y+2xy2+5
3x2y-4xy2-3+5x2y+2xy2+5
=3x2y+5x2y-4xy2+2xy2+5-3
3x2y-4xy2-3+5x2y+2xy2+5
加法交换律
=(3x2y+5x2y)-(4xy2-2xy2)+(5-3)
加法结合律
=(3+5)x2y-(4-2)xy2+(5-3)
=8x2y-2xy2+2
合并同类项的法则:
把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
例3
合并下列多项式中的同类项:
(1)2a2b-3a2b+
解 2a2b-3a2b+
三项都是同类项
(2)a3-a2b+ab2+a2b-ab2+b3
解 a3-a2b+ab2+a2b-ab2+b3
a3-a2b+ab2+a2b-ab2+b3
=a3-a2b+a2b+ab2-ab2+b3
=a3+b3
解 3x2+4x-2x2-x+x2-3x-1
例4
求多项式3x2+4x-2x2-x+x2-3x-1的值,其中x=-3.
先合并同类项
3x2+4x-2x2-x+x2-3x-1
=3x2-2x2+x2+4x-x-3x-1
=(3-2+1)x2+(4-1-3)x-1
=2x2-1
当x=-3时,原式=2×(-3)2-1=17
把x=-3直接代入例4中的多项式,求出它的值.与上面的解法比较一下,哪个解法更简便?
例5
如图所示的窗框,上半部分为半圆,下半部分为6个大小一样的长方形,长方形的长和宽的比为3∶2.
(1)设长方形的长为x米,用x表示所需
材料的长度(重合部分忽略不计);
(2)分别求出当长方形的长为0.4米、0.5
米、0.6米时,所需材料的长度(精
确到0.1米,取π≈3.14).
解 (1) 设长方形的长为x米,则它的宽为 x米.由图不难知道,做这个窗框所需材料的长度为
(2) 当x=0.4时,
当x=0.5时,
(2) 当x=0.6时,
答:当长方形的长为0.4米,所需材料8.1米;长为0.5
米,所需材料10.1米;长为0.6米时,所需材料12.1米.
随堂练习
1.将如图所示的两个圈中的同类项用线连起来.
2.写出3ab2c3的一个同类项.你能写出多少个?
3.k取何值时,-3x2y3k与4x2y6是同类项?
解 2ab2c3, ab2c3, 4ab2c3…,可以写无数个
解 根据题意可知,当-3x2y3k与4x2y6是同类项时
3k=6
解得k=2
当k=2时, -3x2y3k与4x2y6是同类项
1.如果两个同类项的系数互为相反数,那么合并同类项后,结果是___________.
2.先标出下列各多项式中的同类项,再合并同类项:
(1)3x-2x2+5+3x2-2x-5
0
解 3x-2x2+5+3x2-2x-5
=3x-2x-2x2+3x2+5-5
=x+x2
(3) 6a2-5b2+2ab+5b2-6a2
(2)a3+a2b+ab2-a2b-ab2-b3
(2)a3+a2b+ab2-a2b-ab2-b3
=a3+a2b-a2b+ab2-ab2-b3
=a3-b3
(3) 6a2-5b2+2ab+5b2-6a2
=6a2-6a2-5b2+5b2+2ab
=2ab
3.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x3+5xy -2y+1,其中x = ,y =-1.
(1)解 7x2-3x2-2x-2x2+5+6x
=7x2-3x2-2x2-2x+6x+5
=2x2+4x+5
当x=-2时,原式=2×(-2)2+4×(-2)+5=5
3.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x3+5xy -2y+1,其中x = ,y =-1.
(2)解 5a-2b+3b-4a-1
=5a-4a-2b+3b-1
=a+b-1
当a=-1, b=2时,原式=-1+2-1=0
3.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
(3)解 2x2-3xy+y2-2xy-2x2+5xy -2y+1
=2x2-2x2-3xy-2xy+5xy+y2-2y+1
=y2-2y+1
当x = ,y =-1时,原式=(-1)2-2×(-1)+1=4
课堂小结
合并同类项的实际应用
同类项合并同类项
同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项
合并同类项的法则:把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变
利用同类项的概念求字母(或式子)的值
利用合并同类项化简求值
应用
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
03
同类项 合并同类项
情境导入
每个单项式叫做多项式的项.
找出 这个多项式的项:
3x2y-4xy2-3+5x2y+2xy2+5
3x2y,-4xy2, -3, 5x2y, 2xy2, 5
找找这些项中,有哪些具有相同的特征?
3x2y和5x2y
-4xy2和2xy2
-3和5
探索新知
3x2y和5x2y
4xy2和2xy2
3和5
所含字母相同,且x的指数都是2,y的指数都是1
所含字母相同,且x的指数都是1,y的指数都是2
都是常数项
像这样,所含字母相同,并且相同字母的指数也相等的项叫做同类项.所有常数项都是同类项.
例1
指出下列多项式中的同类项:
(1)3x-2y+1+3y-2x-5;
(2)3x2y-2xy2+ - ;
例2
k取何值时,3xky与-x2y是同类项?
解 要使3xky与-x2y是同类项,那么这两项中的x的指数就必须相等,即k=2.
所以当k=2时, 3xky与-x2y是同类项.
如果一个多项式中含有同类项,那么我们可以把同类项合并起来,使结果得以简化.
将同类项3x2y和5x2y合并
3x2y+5x2y=(3+5)x2y =8x2y
对多项式 进行合并:
3x2y-4xy2-3+5x2y+2xy2+5
3x2y-4xy2-3+5x2y+2xy2+5
=3x2y+5x2y-4xy2+2xy2+5-3
3x2y-4xy2-3+5x2y+2xy2+5
加法交换律
=(3x2y+5x2y)-(4xy2-2xy2)+(5-3)
加法结合律
=(3+5)x2y-(4-2)xy2+(5-3)
=8x2y-2xy2+2
合并同类项的法则:
把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变.
例3
合并下列多项式中的同类项:
(1)2a2b-3a2b+
解 2a2b-3a2b+
三项都是同类项
(2)a3-a2b+ab2+a2b-ab2+b3
解 a3-a2b+ab2+a2b-ab2+b3
a3-a2b+ab2+a2b-ab2+b3
=a3-a2b+a2b+ab2-ab2+b3
=a3+b3
解 3x2+4x-2x2-x+x2-3x-1
例4
求多项式3x2+4x-2x2-x+x2-3x-1的值,其中x=-3.
先合并同类项
3x2+4x-2x2-x+x2-3x-1
=3x2-2x2+x2+4x-x-3x-1
=(3-2+1)x2+(4-1-3)x-1
=2x2-1
当x=-3时,原式=2×(-3)2-1=17
把x=-3直接代入例4中的多项式,求出它的值.与上面的解法比较一下,哪个解法更简便?
例5
如图所示的窗框,上半部分为半圆,下半部分为6个大小一样的长方形,长方形的长和宽的比为3∶2.
(1)设长方形的长为x米,用x表示所需
材料的长度(重合部分忽略不计);
(2)分别求出当长方形的长为0.4米、0.5
米、0.6米时,所需材料的长度(精
确到0.1米,取π≈3.14).
解 (1) 设长方形的长为x米,则它的宽为 x米.由图不难知道,做这个窗框所需材料的长度为
(2) 当x=0.4时,
当x=0.5时,
(2) 当x=0.6时,
答:当长方形的长为0.4米,所需材料8.1米;长为0.5
米,所需材料10.1米;长为0.6米时,所需材料12.1米.
随堂练习
1.将如图所示的两个圈中的同类项用线连起来.
2.写出3ab2c3的一个同类项.你能写出多少个?
3.k取何值时,-3x2y3k与4x2y6是同类项?
解 2ab2c3, ab2c3, 4ab2c3…,可以写无数个
解 根据题意可知,当-3x2y3k与4x2y6是同类项时
3k=6
解得k=2
当k=2时, -3x2y3k与4x2y6是同类项
1.如果两个同类项的系数互为相反数,那么合并同类项后,结果是___________.
2.先标出下列各多项式中的同类项,再合并同类项:
(1)3x-2x2+5+3x2-2x-5
0
解 3x-2x2+5+3x2-2x-5
=3x-2x-2x2+3x2+5-5
=x+x2
(3) 6a2-5b2+2ab+5b2-6a2
(2)a3+a2b+ab2-a2b-ab2-b3
(2)a3+a2b+ab2-a2b-ab2-b3
=a3+a2b-a2b+ab2-ab2-b3
=a3-b3
(3) 6a2-5b2+2ab+5b2-6a2
=6a2-6a2-5b2+5b2+2ab
=2ab
3.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x3+5xy -2y+1,其中x = ,y =-1.
(1)解 7x2-3x2-2x-2x2+5+6x
=7x2-3x2-2x2-2x+6x+5
=2x2+4x+5
当x=-2时,原式=2×(-2)2+4×(-2)+5=5
3.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x3+5xy -2y+1,其中x = ,y =-1.
(2)解 5a-2b+3b-4a-1
=5a-4a-2b+3b-1
=a+b-1
当a=-1, b=2时,原式=-1+2-1=0
3.求下列多项式的值:
7x2-3x2-2x-2x2+5+6x,其中x=-2;
5a-2b+3b-4a-1,其中a=-1, b=2;
2x2-3xy+y2-2xy-2x2+5xy -2y+1,其中x = ,y =-1.
(3)解 2x2-3xy+y2-2xy-2x2+5xy -2y+1
=2x2-2x2-3xy-2xy+5xy+y2-2y+1
=y2-2y+1
当x = ,y =-1时,原式=(-1)2-2×(-1)+1=4
课堂小结
合并同类项的实际应用
同类项合并同类项
同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项
合并同类项的法则:把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变
利用同类项的概念求字母(或式子)的值
利用合并同类项化简求值
应用
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
