七年级上册地数学课件-第2章 有理数 单元复习 华师大版(共43张ppt)
文档属性
| 名称 | 七年级上册地数学课件-第2章 有理数 单元复习 华师大版(共43张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 09:21:01 | ||
图片预览










文档简介
华师大版 七年级 上册
02
单元复习
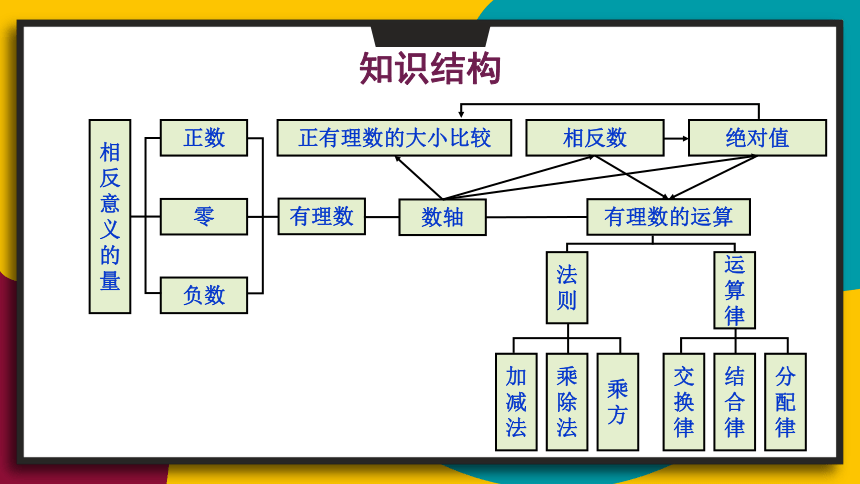
知识结构
有理数的运算
正数
负数
相反意义的量
零
有理数
数轴
正有理数的大小比较
相反数
绝对值
加减法
乘除法
乘方
法则
运算律
交换律
结合律
分配律
释疑解惑
1.为什么要引入负数?举出实例说明正数和负数在表示相反意义的量时的作用.
现实生活中存在很多个有相反意义的量,如:向东5米与向西5米,零上2℃与零下2℃,收入100元与支出100元,低于海平面150米与高出海平面800米……,用正数表示其中一种量,负数表示和它相反意义的量,这样既简单又明白.例如吐鲁番盆地的海拔高度为-155m,表示吐鲁番盆地的海拔高度是低于海平面155m.
2.数的范围从正整数、零和正分数扩充到有理数后,增加了哪些数?减法中哪些原来不能进行的运算可以进行了?
增加了负整数、负分数,解决了原来“小数不能减去大数”的问题,现在任何有理数都可以进行减法运算.
3.怎样用数轴表示有理数?数轴与普通直线有什么不同?怎样用数轴解释绝对值和相反数?
任何一个有理数都可以用数轴上的一个点表示,但数轴上的点不是都表示有理数,这一点,以后我们将要学习.数轴是一条特殊的直线,是规定了正方向、原点和单位长度的直线.原点、正方向、单位长度也称数轴的三要素,缺一不可.
数轴上与原点的距离相等的两个点所表示的数是互为相反数.
4.怎样比较有理数的大小?
有理数的大小比较方法有两种;一是利用数轴,在数轴上较左边的点比右边的点所表示的数小;二是用绝对值,两个负数,绝对值大的反而小.正数大于零,负数小于零.
5.有理数的加法与减法有什么关系?乘法与除法呢?
有理数的减法可以转化为加法,转化的桥梁是相反数,减去一个数等于加上这个数的相反数,同样,除法可以转化为乘法,转化的桥梁是倒数,除以一个数(不为0),等于乘这个数的倒数.有理数的混合运算都可以转化为加法与乘法.
6.有理数满足哪些运算律?
交换律:a+b=b+a、ab=ba
结合律:(a+b)+c=a+(b+c)、(a·b)·c=a(b·c)
分配律:(a+b)·c=ac+bc
其中a、b、c表示任意有理数.
合理使用运算律,可以使计算更简便.
随堂练习
例1 填空:
(1)在知识竞赛中,如果+10分表示加10分,那么扣20分可表示成_______;
(2)某人转动转盘,如果沿逆时针转5圈记作+5圈,那么沿顺时针转12圈可表示成_______;
(3)某次乒乓球质量检测中,一只乒乓球超出标准0.02g记作+0.02g,那么-0.03g可表示成_______ .
-20
-12
低于标准0.03g
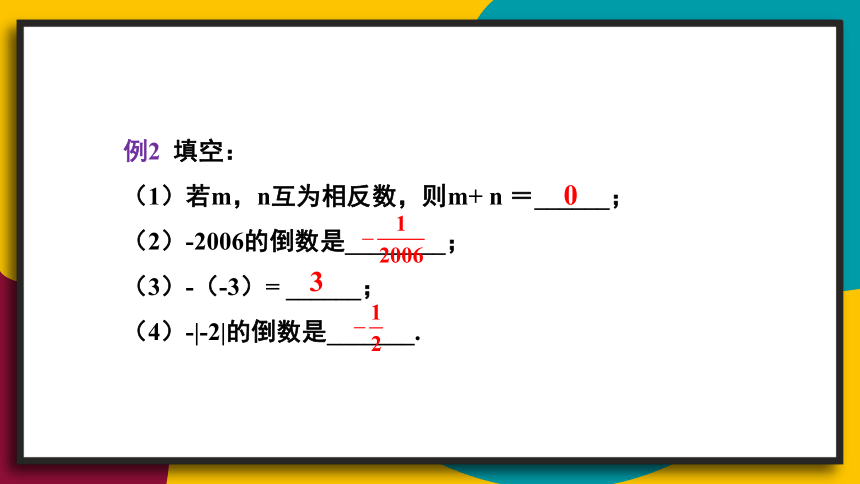
例2 填空:
(1)若m,n互为相反数,则m+ n =______;
(2)-2006的倒数是________;
(3)-(-3)= ______;
(4)-|-2|的倒数是_______.
0
3
例3 如图,数轴上两点所表示的两数( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数
D
例4 下列四个运算中,结果最小的是( )
A.1+(-2) B.1-(-2)
C.1×(-2) D.1÷(-2)
C
例5 如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>-b>-a B.a>-a>b>-b
C.b>a>-b>-a D.-a>b>-b>a
D
例7 神舟六号飞船,在平安飞行115小时23分后重返神州. 用科学记数法表示神舟六号飞船飞行的时间是______________秒 (精确到千位).
分析:a×10x中a的取值范围是1≤a<10,底数10的指数n等于所表示的整数位数减去1.
4.15×105
例8 (-8)2014+(-8)2013能被下列数整除的是( )
A.3 B.5 C.7 D.9
C
巩固练习
正数:2.5、 、0.05;
负数:-8、-0.7、- ;
2
2
7.5
7.5
0
0
没有倒数
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
6
-1.6
0
2.5
-3< <-1.6<0<2.5<
5>0.6> >-0.6>-3.2>-3.3
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
6
其中最大的是3.
-1.17>-1.2
=57
=-50
=-36
=-17
=120
=16
=7
=-216
=3
=3
=-80
=5
=-24
=25
(2)立方等于27的有理数有一个,是3,立方等于-27的有理数有一个,是-3.
(1)平方等于 的有理数有 和 ;
没有平方等于 的有理数.
(1)互为相反数的两数和是0.
(2)如果两个互为相反数的数都不为0,那么它们的商是-1.
(1)2.77
(2)0.009
(3)9.0
(4)1.7×104
≈40.5
≈ 70.0
≈ 48.3
(1) 0和1之间的数的平方和立方都比原数小,例如0.12=0.01 <0.1,0.13=0.001 <0.1;其倒数比原数大,例如 .
(2) -1和0之间的数的平方和立方所得结果都比原数大,例如(-0.1)2 =0.01>-0.1,(0.1)3=-0.001>-0.1.其倒数比原数小,例如 .
C
D
C
=-16
=4
(1)正确,因为a(a>0)的倒数是 ,两个倒数都是正数,分子都是1,分母较大的数较小;
(2)不正确,例如正数的倒数比负数的倒数大;
(1)4
(2)7.5
(3)3.5
+15-2+5-3+8-3-1+11+4-5-2+7-3+5=36(千米)
答:收工时,检修小组在A地的东边,距离A地36千米.
1.3×5×107=6.5×107(cm)=6.5×105(m)
答:两地的实际距离为6.5×105(m).
V圆柱=πR2h=π×0.472×0.820≈0.57(m3)
答:圆柱的体积为0.57 m3.
合格品的直径最大:30+0.03=30.03mm
合格品的直径最小:30-0.02=29.98mm
答:合格品的直径最大:30.03mm;
合格品的直径最小:29.98mm.
(1)a取正数或零;
(2)a取负数;
(3)a取负数或零;
(4)a取正数;
(1)不一定,因为m和n可以互为相反数,例如﹣2和2;
(2)一定,因为由|m|=|n|可以得到|m|2=|n|2,即m2=n2.
6
猜测:从1开始的n个连续奇数之和等于n2.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
02
单元复习
知识结构
有理数的运算
正数
负数
相反意义的量
零
有理数
数轴
正有理数的大小比较
相反数
绝对值
加减法
乘除法
乘方
法则
运算律
交换律
结合律
分配律
释疑解惑
1.为什么要引入负数?举出实例说明正数和负数在表示相反意义的量时的作用.
现实生活中存在很多个有相反意义的量,如:向东5米与向西5米,零上2℃与零下2℃,收入100元与支出100元,低于海平面150米与高出海平面800米……,用正数表示其中一种量,负数表示和它相反意义的量,这样既简单又明白.例如吐鲁番盆地的海拔高度为-155m,表示吐鲁番盆地的海拔高度是低于海平面155m.
2.数的范围从正整数、零和正分数扩充到有理数后,增加了哪些数?减法中哪些原来不能进行的运算可以进行了?
增加了负整数、负分数,解决了原来“小数不能减去大数”的问题,现在任何有理数都可以进行减法运算.
3.怎样用数轴表示有理数?数轴与普通直线有什么不同?怎样用数轴解释绝对值和相反数?
任何一个有理数都可以用数轴上的一个点表示,但数轴上的点不是都表示有理数,这一点,以后我们将要学习.数轴是一条特殊的直线,是规定了正方向、原点和单位长度的直线.原点、正方向、单位长度也称数轴的三要素,缺一不可.
数轴上与原点的距离相等的两个点所表示的数是互为相反数.
4.怎样比较有理数的大小?
有理数的大小比较方法有两种;一是利用数轴,在数轴上较左边的点比右边的点所表示的数小;二是用绝对值,两个负数,绝对值大的反而小.正数大于零,负数小于零.
5.有理数的加法与减法有什么关系?乘法与除法呢?
有理数的减法可以转化为加法,转化的桥梁是相反数,减去一个数等于加上这个数的相反数,同样,除法可以转化为乘法,转化的桥梁是倒数,除以一个数(不为0),等于乘这个数的倒数.有理数的混合运算都可以转化为加法与乘法.
6.有理数满足哪些运算律?
交换律:a+b=b+a、ab=ba
结合律:(a+b)+c=a+(b+c)、(a·b)·c=a(b·c)
分配律:(a+b)·c=ac+bc
其中a、b、c表示任意有理数.
合理使用运算律,可以使计算更简便.
随堂练习
例1 填空:
(1)在知识竞赛中,如果+10分表示加10分,那么扣20分可表示成_______;
(2)某人转动转盘,如果沿逆时针转5圈记作+5圈,那么沿顺时针转12圈可表示成_______;
(3)某次乒乓球质量检测中,一只乒乓球超出标准0.02g记作+0.02g,那么-0.03g可表示成_______ .
-20
-12
低于标准0.03g
例2 填空:
(1)若m,n互为相反数,则m+ n =______;
(2)-2006的倒数是________;
(3)-(-3)= ______;
(4)-|-2|的倒数是_______.
0
3
例3 如图,数轴上两点所表示的两数( )
A.和为正数 B.和为负数
C.积为正数 D.积为负数
D
例4 下列四个运算中,结果最小的是( )
A.1+(-2) B.1-(-2)
C.1×(-2) D.1÷(-2)
C
例5 如果a<0,b>0,a+b<0,那么下列关系式中正确的是( )
A.a>b>-b>-a B.a>-a>b>-b
C.b>a>-b>-a D.-a>b>-b>a
D
例7 神舟六号飞船,在平安飞行115小时23分后重返神州. 用科学记数法表示神舟六号飞船飞行的时间是______________秒 (精确到千位).
分析:a×10x中a的取值范围是1≤a<10,底数10的指数n等于所表示的整数位数减去1.
4.15×105
例8 (-8)2014+(-8)2013能被下列数整除的是( )
A.3 B.5 C.7 D.9
C
巩固练习
正数:2.5、 、0.05;
负数:-8、-0.7、- ;
2
2
7.5
7.5
0
0
没有倒数
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
6
-1.6
0
2.5
-3< <-1.6<0<2.5<
5>0.6> >-0.6>-3.2>-3.3
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
6
其中最大的是3.
-1.17>-1.2
=57
=-50
=-36
=-17
=120
=16
=7
=-216
=3
=3
=-80
=5
=-24
=25
(2)立方等于27的有理数有一个,是3,立方等于-27的有理数有一个,是-3.
(1)平方等于 的有理数有 和 ;
没有平方等于 的有理数.
(1)互为相反数的两数和是0.
(2)如果两个互为相反数的数都不为0,那么它们的商是-1.
(1)2.77
(2)0.009
(3)9.0
(4)1.7×104
≈40.5
≈ 70.0
≈ 48.3
(1) 0和1之间的数的平方和立方都比原数小,例如0.12=0.01 <0.1,0.13=0.001 <0.1;其倒数比原数大,例如 .
(2) -1和0之间的数的平方和立方所得结果都比原数大,例如(-0.1)2 =0.01>-0.1,(0.1)3=-0.001>-0.1.其倒数比原数小,例如 .
C
D
C
=-16
=4
(1)正确,因为a(a>0)的倒数是 ,两个倒数都是正数,分子都是1,分母较大的数较小;
(2)不正确,例如正数的倒数比负数的倒数大;
(1)4
(2)7.5
(3)3.5
+15-2+5-3+8-3-1+11+4-5-2+7-3+5=36(千米)
答:收工时,检修小组在A地的东边,距离A地36千米.
1.3×5×107=6.5×107(cm)=6.5×105(m)
答:两地的实际距离为6.5×105(m).
V圆柱=πR2h=π×0.472×0.820≈0.57(m3)
答:圆柱的体积为0.57 m3.
合格品的直径最大:30+0.03=30.03mm
合格品的直径最小:30-0.02=29.98mm
答:合格品的直径最大:30.03mm;
合格品的直径最小:29.98mm.
(1)a取正数或零;
(2)a取负数;
(3)a取负数或零;
(4)a取正数;
(1)不一定,因为m和n可以互为相反数,例如﹣2和2;
(2)一定,因为由|m|=|n|可以得到|m|2=|n|2,即m2=n2.
6
猜测:从1开始的n个连续奇数之和等于n2.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
