华师大版七年级上册数学第2章 有理数-2.3 相反数 课件(19张PPT)
文档属性
| 名称 | 华师大版七年级上册数学第2章 有理数-2.3 相反数 课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-12 00:00:00 | ||
图片预览




文档简介
华师大版 七年级 上册
02
2.3 相反数
情境导入
(并标上字母)
探究新知
观察这两对数,各有哪些相同?哪些不同?
数字相同,
符号不同,一正一负
像6和﹣6、1.5和﹣1.5那样,只有正负号不同的两个数互称为相反数.
也称这两个数互为相反数。
-6
6
与
-1.5
1.5
与
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
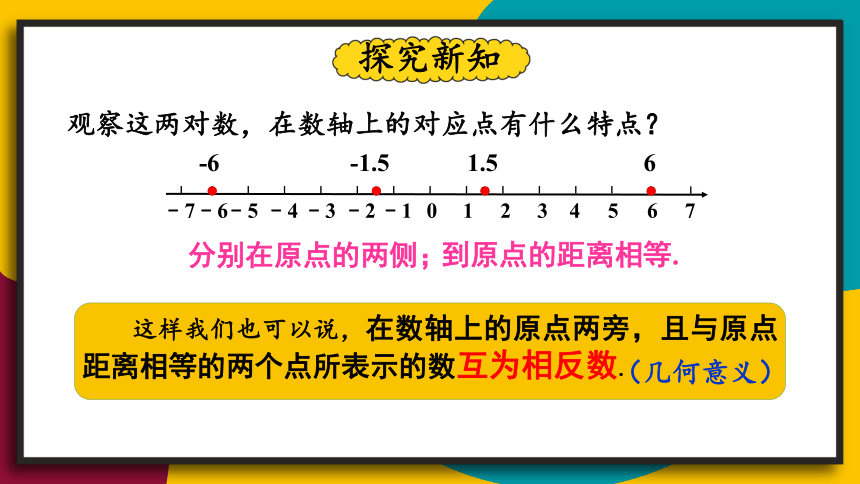
观察这两对数,在数轴上的对应点有什么特点?
探究新知
分别在原点的两侧;
到原点的距离相等.
这样我们也可以说,在数轴上的原点两旁,且与原点距离相等的两个点所表示的数互为相反数.
(几何意义)
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
探究新知
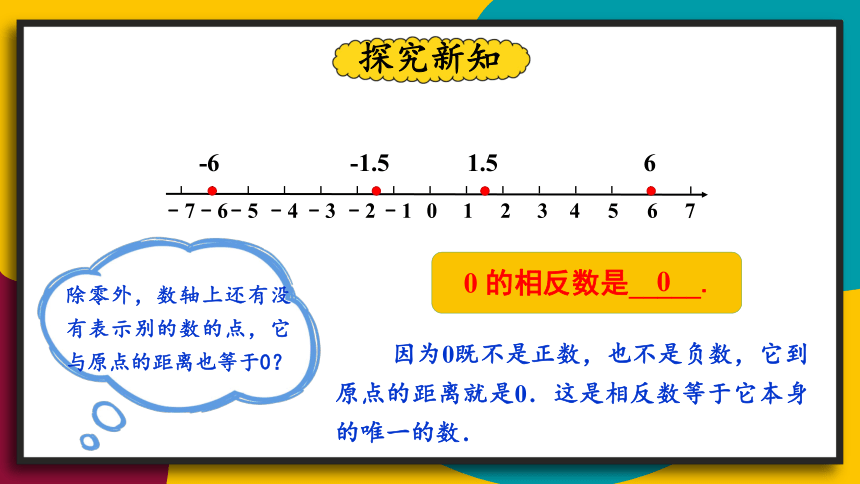
0 的相反数是_____.
0
除零外,数轴上还有没有表示别的数的点,它与原点的距离也等于0?
因为0既不是正数,也不是负数,它到原点的距离就是0.这是相反数等于它本身的唯一的数.
思考:
探究新知
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
a
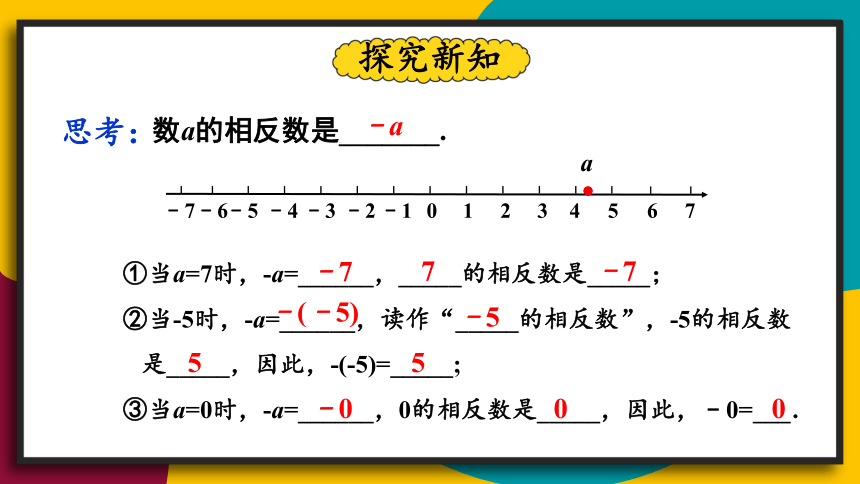
数a的相反数是_______.
﹣a
①当a=7时,-a=______,_____的相反数是_____;
②当-5时,-a=______,读作“_____的相反数”,-5的相反数
是_____,因此,-(-5)=_____;
③当a=0时,-a=______,0的相反数是_____,因此,﹣0=___.
﹣7
7
﹣7
﹣(﹣5)
﹣5
5
5
﹣0
0
0
探究新知
思考:
那么-(-8) , -(+4) , -(- )各表示什么意思?
-(-8)=8 表示-8的相反数;
-(+4)=-4 表示+4的相反数;
-(- )= 表示- 的相反数;
你能自己总结出简化符号的规律吗?
括号外的符号与括号内的符号同号,则简化符号后的数是正数;
括号内、外的符号是异号,则简化符号后的数是负数.
探究新知
思考:
那么-(-8) , -(+4) , -(- )各表示什么意思?
你能自己总结出简化符号的规律吗?
同号为正;异号为负.
-(-8)=8 表示-8的相反数;
-(+4)=-4 表示+4的相反数;
-(- )= 表示- 的相反数;
分别写出下列各数的相反数:
例1
﹢5,﹣7, , 11.2.
解
﹣(﹢5)=﹣5
﹣(﹣7)=7
﹣( )=
﹣(11.2)=﹣11.2
化简:
例2
(1)﹣(﹢10)
(2)+(﹣0.15)
(3)﹢(﹢3)
(4)﹣(﹣20)
解
(1)﹣(﹢10)=﹣10
(2)+(﹣0.15)=﹣0.15
(3)﹢(﹢3)=﹢3=3
(4)﹣(﹣20)=20
巩固练习
﹣2.5
100
1.1
﹣8.2
(1)﹣(﹢0.78)=﹣0.78
(3)﹣(﹣3.14)=3.14
(4)﹢(﹣10.1)=﹣10.1
(2)﹢(﹢ )=
(1)不正确,例如﹢3和﹣5的正负号相反,但它们不互为相反数;
(2)不正确,例如 和2的互为倒数,但它们不互为相反数;
(3)正确,符合相反数的意义;
2.5
﹣1
0
10
2
0
3.75
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
﹣2
2
0
﹣3.75
﹣3.75
(1)﹣(﹣16)=16
(2)﹣(﹢25)=﹣25
(3)﹢(﹣12)=﹣12
(4)﹢(﹢2.1)=2.1
(5)﹣(﹢33)=﹣33
(6)﹣(﹣ )=
负数
0
正数
课堂小结
1.什么样的两个数叫做互为相反数?
2.互为相反数的两个数在数轴上的位置有什么关系?
3.怎样化简多重符号?
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
02
2.3 相反数
情境导入
(并标上字母)
探究新知
观察这两对数,各有哪些相同?哪些不同?
数字相同,
符号不同,一正一负
像6和﹣6、1.5和﹣1.5那样,只有正负号不同的两个数互称为相反数.
也称这两个数互为相反数。
-6
6
与
-1.5
1.5
与
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
观察这两对数,在数轴上的对应点有什么特点?
探究新知
分别在原点的两侧;
到原点的距离相等.
这样我们也可以说,在数轴上的原点两旁,且与原点距离相等的两个点所表示的数互为相反数.
(几何意义)
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
-1.5
1.5
-6
6
探究新知
0 的相反数是_____.
0
除零外,数轴上还有没有表示别的数的点,它与原点的距离也等于0?
因为0既不是正数,也不是负数,它到原点的距离就是0.这是相反数等于它本身的唯一的数.
思考:
探究新知
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
a
数a的相反数是_______.
﹣a
①当a=7时,-a=______,_____的相反数是_____;
②当-5时,-a=______,读作“_____的相反数”,-5的相反数
是_____,因此,-(-5)=_____;
③当a=0时,-a=______,0的相反数是_____,因此,﹣0=___.
﹣7
7
﹣7
﹣(﹣5)
﹣5
5
5
﹣0
0
0
探究新知
思考:
那么-(-8) , -(+4) , -(- )各表示什么意思?
-(-8)=8 表示-8的相反数;
-(+4)=-4 表示+4的相反数;
-(- )= 表示- 的相反数;
你能自己总结出简化符号的规律吗?
括号外的符号与括号内的符号同号,则简化符号后的数是正数;
括号内、外的符号是异号,则简化符号后的数是负数.
探究新知
思考:
那么-(-8) , -(+4) , -(- )各表示什么意思?
你能自己总结出简化符号的规律吗?
同号为正;异号为负.
-(-8)=8 表示-8的相反数;
-(+4)=-4 表示+4的相反数;
-(- )= 表示- 的相反数;
分别写出下列各数的相反数:
例1
﹢5,﹣7, , 11.2.
解
﹣(﹢5)=﹣5
﹣(﹣7)=7
﹣( )=
﹣(11.2)=﹣11.2
化简:
例2
(1)﹣(﹢10)
(2)+(﹣0.15)
(3)﹢(﹢3)
(4)﹣(﹣20)
解
(1)﹣(﹢10)=﹣10
(2)+(﹣0.15)=﹣0.15
(3)﹢(﹢3)=﹢3=3
(4)﹣(﹣20)=20
巩固练习
﹣2.5
100
1.1
﹣8.2
(1)﹣(﹢0.78)=﹣0.78
(3)﹣(﹣3.14)=3.14
(4)﹢(﹣10.1)=﹣10.1
(2)﹢(﹢ )=
(1)不正确,例如﹢3和﹣5的正负号相反,但它们不互为相反数;
(2)不正确,例如 和2的互为倒数,但它们不互为相反数;
(3)正确,符合相反数的意义;
2.5
﹣1
0
10
2
0
3.75
0
1
2
3
﹣1
﹣2
﹣3
﹣4
4
﹣5
5
﹣6
﹣7
6
7
﹣2
2
0
﹣3.75
﹣3.75
(1)﹣(﹣16)=16
(2)﹣(﹢25)=﹣25
(3)﹢(﹣12)=﹣12
(4)﹢(﹢2.1)=2.1
(5)﹣(﹢33)=﹣33
(6)﹣(﹣ )=
负数
0
正数
课堂小结
1.什么样的两个数叫做互为相反数?
2.互为相反数的两个数在数轴上的位置有什么关系?
3.怎样化简多重符号?
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
