人教版五年级上册数学5.2.4.4 实际问题与方程(4)课件(26张PPT)
文档属性
| 名称 | 人教版五年级上册数学5.2.4.4 实际问题与方程(4)课件(26张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 09:29:10 | ||
图片预览





文档简介
(共26张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
第11课时 实际问题与方程(4)
简易方程
5
1. 初步学会解决含有两个未知数的实际问题,会设其中一个量为x,另一个量用含有x的式子表示。
2. 经历解形如ax±x=b方程的步骤和过程,掌握解此类方程的方法和策略。
3. 在解方程过程中培养代数思想和符号意识,以及方程思维和方程意识,体会用方程解决问题的优势。
学习目标
【重点】
初步学会解决含有两个未知数的实际问题。
【难点】
当有两个未知量时,如何合理假设未知数。
课堂导入
填一填。
(1)舞蹈组有男生x人,女生人数是男生的2倍,女生有( )人,男、女生共有( )人。
(2)城郊中学图书馆有科技书m本,故事书的本数是科技书的1.8倍,那么,m+1.8m表示(
), 1.8m-m表示( )。
2x
3x
故事书和科技书一
共的本数
故事书比科技书多的本书
新知探究
4
(教材第78页例4)
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4 倍。
地球上的海洋面积
和陆地面积分别是
多少亿平方千米
从题目中你获得了哪些条件?
要求什么问题?
4
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4 倍。
地球上的海洋面积
和陆地面积分别是
多少亿平方千米
这道题和我们以前学过的题有什么不同之处?
题中的两个量都是未知数。
4
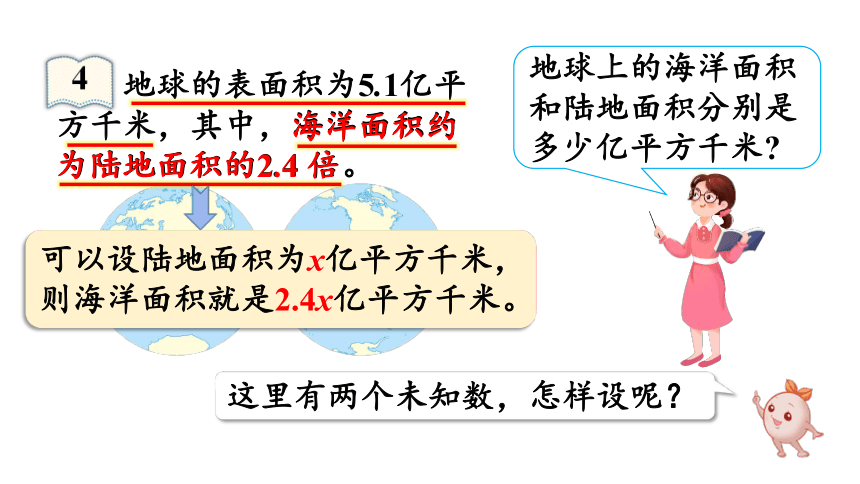
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4 倍。
地球上的海洋面积
和陆地面积分别是
多少亿平方千米
这里有两个未知数,怎样设呢?
海洋面积约
为陆地面积的2.4 倍
可以设陆地面积为x亿平方千米,则海洋面积就是2.4x亿平方千米。
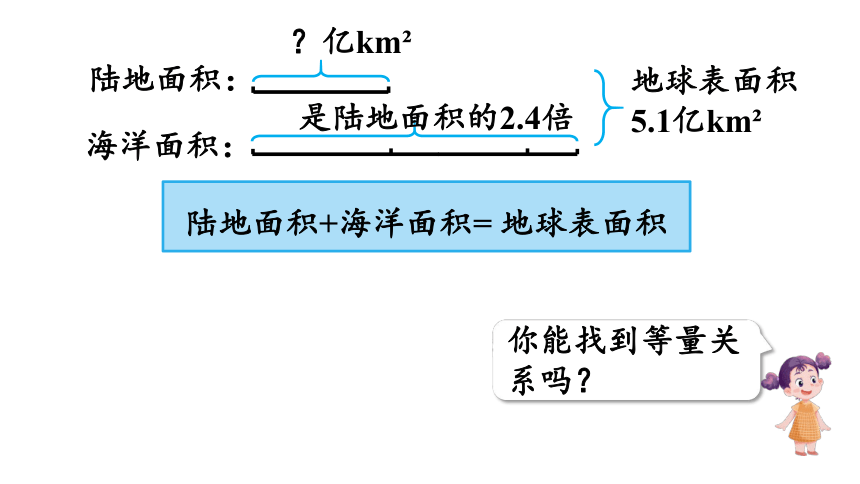
海洋面积:
陆地面积:
?亿km
是陆地面积的2.4倍
地球表面积5.1亿km
你能找到等量关系吗?
陆地面积+海洋面积= 地球表面积
陆地面积+海洋面积= 地球表面积
解:设陆地面积为x亿平方千米。那么海洋面积为2.4x亿平方千米。
x+2.4x = 5.1
(1+2.4)x = 5.1
3.4x = 5.1
3.4x÷3.4 = 5.1÷3.4
x = 1.5
运用了什么运算定律?
陆地面积是1.5亿平方千米,那海洋面积呢?
答:陆地面积是1.5亿平方千米,那海洋面积3.6亿平方千米。
2.4x=2.4×1.5=3.6
3.6+1.5=5.1(亿平方千米);3.6÷1.5=2.4
所求答案与已知条件完全一致,说明所求结果是正确的。
5.1-1.5=3.6(亿平方千米)
检验
小组交流:还可以列什么方程解答这道题呢?
陆地面积+海洋面积=地球表面积
解:设海洋面积为x亿平方千米,则陆地面积为x÷2.4亿平方千米。
x+x÷2.4=5.1
海洋面积÷陆地面积=2.4
解:设陆地面积为x亿平方千米,则海洋面积为
(5.1 x)亿平方千米。
(5.1 x)÷x=2.4
小组交流:这三种方程,哪种比较好呢?
在解这类问题时,用倍数关系来假设,用和差关系来列方程比较简便。
x+x÷2.4=5.1
x+2.4x = 5.1
(5.1 x)÷x=2.4
这个方程比较简明易懂,而且求解比较方便。
这两个方程,一个不会解,一个很麻烦。
课堂练习
做一做
1.
(教材第78页“做一做”)
果园里种着桃树和杏树,杏树的棵数是桃树的3倍。
x+3x=180
(1+3)x=180
4x=180
4x÷4 =180÷4
x=45
解:设桃树有x棵,则杏树为3x棵 。
45×3=135(棵)
答:桃树有45棵,杏树有135棵。
(1)桃树和杏树一共有180棵,桃树和杏树各有多少棵?
设桃树为x棵。
桃树棵数+杏树棵数= 180
果园里种着桃树和杏树,杏树的棵数是桃树的3倍。
3x x=90
(3 1)x=90
2x=90
2x÷2 =90÷2
x=45
解:设桃树有x棵,则杏树为3x棵 。
45+90=135(棵)
(2)杏树比桃树多90棵,桃树和杏树各有多少棵?
杏树棵数-桃树棵数= 90
做一做
1.
答:桃树有45棵,杏树有135棵。
解:设鸡、兔各有x只。
2x+4x = 48
6x = 48
x = 8
答:鸡、兔各有8只。
同学们,你们听说过 “鸡兔同笼”问题吗?
2.
(教材第80页第6题)
注意隐藏的条件:鸡有两只脚,兔有四只脚。
和 的数量相同,两种动物的腿加起来共有48条。
和 各有多少只?
(教材第80页第7题)
3.
小明和妈妈今年分别多少岁?
小明:
妈妈:
x岁
比小明大24岁
3倍
可用倍数关系设未知数,用差关系列方程。
3.
解:设小明今年x岁,那么妈妈今年3x岁。
3x-x = 24
2x = 24
x = 12
3x = 12×3 = 36
答:小明今年12岁,妈妈今年36岁。
小明和妈妈今年分别多少岁?
(教材第80页第8题)
解:设较小的自然数是x,另一个则为(x+1)。
x+(x+1)= 97
2x+1 = 97
2x = 96
x = 48
x+1 = 49
答:这两个自然数分别是48、49。
4. 两个相邻自然数的和是97,这两个自然数分别是多少?
也可以设较大的自然数为x,另一个则为(x-1)
5. 学校买来一批篮球和足球,篮球比足球多10,且篮球的个数是足球的1.2倍,学校买来篮球和足球各多少个?
篮球个数-足球个数=多的个数
解:设买来足球x个,则买来足球1.2x个。
1.2x-x = 10
0.2x = 10
0.2x÷0.2 = 10÷0.2
x = 50
1.2x=1.2×50=60
答:学校买来篮球60个、足球50个。
可用倍数关系假设,用差关系列方程。
(教材第81页第10*题)
提升练习
假设□代表的数是x,则等式可以转化为方程:
24 x-15x = 18
9x = 18
x = 2
所以在□里填2时,等式成立。
1.在下面的两个 里填入相同的数,使等式成立。
24× - ×15 = 18
可以把□里的数看作同一个未知数。
2. 琳琳和乐乐一起叠纸鹤,其中乐乐叠的个数是琳琳的
1.5倍,而乐乐如果把叠的纸鹤给琳琳4个,则两人就一
样多。两人分别叠了多少个纸鹤?
琳琳
乐乐
乐乐叠的个数是琳琳的1.5倍
4个
4个
一样多
多8个
乐乐叠的个数-琳琳叠的个数=4×2
乐乐叠的个数-琳琳叠的个数=4×2
解:设琳琳叠了x个,则乐乐叠了1.5x个。
1.5x-x = 4×2
0.5x = 8
0.5x÷0.5 = 8÷0.5
x = 16
1.5x=1.5×16=24
答:琳琳叠了16个,则乐乐叠了24个。
课堂小结
这节课你有什么收获?
解有两个未知数的实际问题的方法
1.利用倍数关系来假设;
2.利用和差关系来列方程;
3.解方程,并检验作答。
人教版数学
五年级上册
人教版数学五年级(上)
第11课时 实际问题与方程(4)
简易方程
5
1. 初步学会解决含有两个未知数的实际问题,会设其中一个量为x,另一个量用含有x的式子表示。
2. 经历解形如ax±x=b方程的步骤和过程,掌握解此类方程的方法和策略。
3. 在解方程过程中培养代数思想和符号意识,以及方程思维和方程意识,体会用方程解决问题的优势。
学习目标
【重点】
初步学会解决含有两个未知数的实际问题。
【难点】
当有两个未知量时,如何合理假设未知数。
课堂导入
填一填。
(1)舞蹈组有男生x人,女生人数是男生的2倍,女生有( )人,男、女生共有( )人。
(2)城郊中学图书馆有科技书m本,故事书的本数是科技书的1.8倍,那么,m+1.8m表示(
), 1.8m-m表示( )。
2x
3x
故事书和科技书一
共的本数
故事书比科技书多的本书
新知探究
4
(教材第78页例4)
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4 倍。
地球上的海洋面积
和陆地面积分别是
多少亿平方千米
从题目中你获得了哪些条件?
要求什么问题?
4
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4 倍。
地球上的海洋面积
和陆地面积分别是
多少亿平方千米
这道题和我们以前学过的题有什么不同之处?
题中的两个量都是未知数。
4
地球的表面积为5.1亿平方千米,其中,海洋面积约为陆地面积的2.4 倍。
地球上的海洋面积
和陆地面积分别是
多少亿平方千米
这里有两个未知数,怎样设呢?
海洋面积约
为陆地面积的2.4 倍
可以设陆地面积为x亿平方千米,则海洋面积就是2.4x亿平方千米。
海洋面积:
陆地面积:
?亿km
是陆地面积的2.4倍
地球表面积5.1亿km
你能找到等量关系吗?
陆地面积+海洋面积= 地球表面积
陆地面积+海洋面积= 地球表面积
解:设陆地面积为x亿平方千米。那么海洋面积为2.4x亿平方千米。
x+2.4x = 5.1
(1+2.4)x = 5.1
3.4x = 5.1
3.4x÷3.4 = 5.1÷3.4
x = 1.5
运用了什么运算定律?
陆地面积是1.5亿平方千米,那海洋面积呢?
答:陆地面积是1.5亿平方千米,那海洋面积3.6亿平方千米。
2.4x=2.4×1.5=3.6
3.6+1.5=5.1(亿平方千米);3.6÷1.5=2.4
所求答案与已知条件完全一致,说明所求结果是正确的。
5.1-1.5=3.6(亿平方千米)
检验
小组交流:还可以列什么方程解答这道题呢?
陆地面积+海洋面积=地球表面积
解:设海洋面积为x亿平方千米,则陆地面积为x÷2.4亿平方千米。
x+x÷2.4=5.1
海洋面积÷陆地面积=2.4
解:设陆地面积为x亿平方千米,则海洋面积为
(5.1 x)亿平方千米。
(5.1 x)÷x=2.4
小组交流:这三种方程,哪种比较好呢?
在解这类问题时,用倍数关系来假设,用和差关系来列方程比较简便。
x+x÷2.4=5.1
x+2.4x = 5.1
(5.1 x)÷x=2.4
这个方程比较简明易懂,而且求解比较方便。
这两个方程,一个不会解,一个很麻烦。
课堂练习
做一做
1.
(教材第78页“做一做”)
果园里种着桃树和杏树,杏树的棵数是桃树的3倍。
x+3x=180
(1+3)x=180
4x=180
4x÷4 =180÷4
x=45
解:设桃树有x棵,则杏树为3x棵 。
45×3=135(棵)
答:桃树有45棵,杏树有135棵。
(1)桃树和杏树一共有180棵,桃树和杏树各有多少棵?
设桃树为x棵。
桃树棵数+杏树棵数= 180
果园里种着桃树和杏树,杏树的棵数是桃树的3倍。
3x x=90
(3 1)x=90
2x=90
2x÷2 =90÷2
x=45
解:设桃树有x棵,则杏树为3x棵 。
45+90=135(棵)
(2)杏树比桃树多90棵,桃树和杏树各有多少棵?
杏树棵数-桃树棵数= 90
做一做
1.
答:桃树有45棵,杏树有135棵。
解:设鸡、兔各有x只。
2x+4x = 48
6x = 48
x = 8
答:鸡、兔各有8只。
同学们,你们听说过 “鸡兔同笼”问题吗?
2.
(教材第80页第6题)
注意隐藏的条件:鸡有两只脚,兔有四只脚。
和 的数量相同,两种动物的腿加起来共有48条。
和 各有多少只?
(教材第80页第7题)
3.
小明和妈妈今年分别多少岁?
小明:
妈妈:
x岁
比小明大24岁
3倍
可用倍数关系设未知数,用差关系列方程。
3.
解:设小明今年x岁,那么妈妈今年3x岁。
3x-x = 24
2x = 24
x = 12
3x = 12×3 = 36
答:小明今年12岁,妈妈今年36岁。
小明和妈妈今年分别多少岁?
(教材第80页第8题)
解:设较小的自然数是x,另一个则为(x+1)。
x+(x+1)= 97
2x+1 = 97
2x = 96
x = 48
x+1 = 49
答:这两个自然数分别是48、49。
4. 两个相邻自然数的和是97,这两个自然数分别是多少?
也可以设较大的自然数为x,另一个则为(x-1)
5. 学校买来一批篮球和足球,篮球比足球多10,且篮球的个数是足球的1.2倍,学校买来篮球和足球各多少个?
篮球个数-足球个数=多的个数
解:设买来足球x个,则买来足球1.2x个。
1.2x-x = 10
0.2x = 10
0.2x÷0.2 = 10÷0.2
x = 50
1.2x=1.2×50=60
答:学校买来篮球60个、足球50个。
可用倍数关系假设,用差关系列方程。
(教材第81页第10*题)
提升练习
假设□代表的数是x,则等式可以转化为方程:
24 x-15x = 18
9x = 18
x = 2
所以在□里填2时,等式成立。
1.在下面的两个 里填入相同的数,使等式成立。
24× - ×15 = 18
可以把□里的数看作同一个未知数。
2. 琳琳和乐乐一起叠纸鹤,其中乐乐叠的个数是琳琳的
1.5倍,而乐乐如果把叠的纸鹤给琳琳4个,则两人就一
样多。两人分别叠了多少个纸鹤?
琳琳
乐乐
乐乐叠的个数是琳琳的1.5倍
4个
4个
一样多
多8个
乐乐叠的个数-琳琳叠的个数=4×2
乐乐叠的个数-琳琳叠的个数=4×2
解:设琳琳叠了x个,则乐乐叠了1.5x个。
1.5x-x = 4×2
0.5x = 8
0.5x÷0.5 = 8÷0.5
x = 16
1.5x=1.5×16=24
答:琳琳叠了16个,则乐乐叠了24个。
课堂小结
这节课你有什么收获?
解有两个未知数的实际问题的方法
1.利用倍数关系来假设;
2.利用和差关系来列方程;
3.解方程,并检验作答。
