人教版五年级上册数学5 简易方程练习十二课件(29张PPT)
文档属性
| 名称 | 人教版五年级上册数学5 简易方程练习十二课件(29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 09:42:35 | ||
图片预览







文档简介
(共29张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
练习十二
简易方程
5
重点回顾
用字母表示数及用含有字母的式子表示数量关系时,需要注意什么?
1.含有字母的式子中乘号可以省略,数字在字母前面。
2.用含有字母的式子表示生活中的数量关系时,字母
所取的数值要符合实际情况。
3.表示同一个数量时要用同一个未知数。
4.较复杂的式子,要根据乘法分配律进行计算或化简。
如何求含有字母的式子表示学过的运算定律或公式?
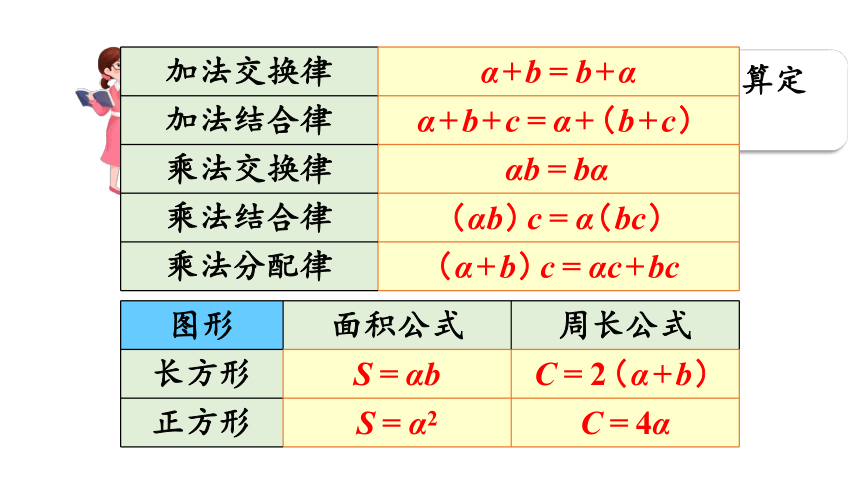
加法交换律 α+b=b+α
加法结合律 α+b+c=α+(b+c)
乘法交换律 αb=bα
乘法结合律 (αb)c=α(bc)
乘法分配律 (α+b)c=αc+bc
图形 面积公式 周长公式
长方形 S=αb C=2(α+b)
正方形 S=α2 C=4α
练习巩固
(教材第55页练习十二)
-105
如果我们用字母x表示身高,那么……
我们也可以用其他字母表示身高,比如h等。
1.成年男子的标准体重通常用下面的式子表示:
用含有字母的式子表示出成年男子的标准体重。
______________________
标准体重=身高-105
身高用厘米数,体重用千克数。
x
你能用它算出你爸爸的标准体重应是多少吗?
我爸爸的身高是1米72厘米,那么他的标准体重应该是多少呢?
1.成年男子的标准体重通常用下面的式子表示:
用含有字母的式子表示出成年男子的标准体重。
______________________
标准体重=身高-105
x-105
身高用厘米数,体重用千克数。
x-105=172-105=67(kg)
1米72厘米=172厘米
答:爸爸的标准体重应该是67kg。
我爸体重是80kg,那该减肥啦!
1.成年男子的标准体重通常用下面的式子表示:
用含有字母的式子表示出成年男子的标准体重。
______________________
标准体重=身高-105
x-105
身高用厘米数,体重用千克数。
你能用它算出你爸爸的标准体重应是多少吗?
2.
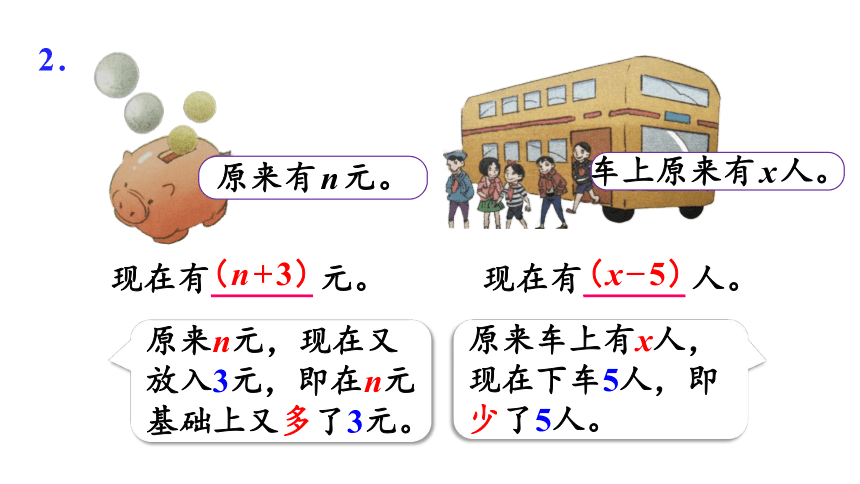
原来有n元。
现在有 元。
(n+3)
车上原来有x人。
现在有 人。
(x 5)
原来n元,现在又放入3元,即在n元基础上又多了3元。
原来车上有x人,现在下车5人,即少了5人。
有m个饺子(m 为整十数), 每盘装10个。可以装 盘。
每袋有a条鱼,
一共有 条。
m÷10
3a
求3个a是多少用乘法计算。
求m里面有多少个10用除法计算。
2.
3.(1)我国青少年(7~17 岁)在1980年平均身高x cm,到2000年,平均身高增长了6cm。
(x+6)
2000年我国青少年平均身高 cm。
1980年的平均身高 + 6 = 2000年的平均身高
x
+ 6
3.(1)
0.18a
装上翅膀,怎么也飞不起来?
你们的骨骼太重!
鸟的骨骼约是体重的0.05~0.06倍,人的骨骼约是体重
的0.18倍。一个人重a kg,骨骼约是 kg。
3.(2)
早上身高 - 2 =晚上身高
人的身高早晚可能会相差2cm,在早上最高,晚上最矮。一个人早 上身高 bcm,晚上身高可能是 cm。
(b-2)
依题意,人晚上身高比早上身高少2厘米。
b
- 2
真的是这样吗?那我现在的身高132厘米,早上应高一点,而晚上就要矮一点啰。
3.(3)
小英家本月的用电量是80千瓦时,交电费c元,那么电费每千瓦时是 元。
c÷ 80
单价=总价÷数量
我明白了:用字母表示数量关系时,可以把字母看作普通的数来进行思考。
总价
求单价
数量
3.(4)
(1)今天卖出足球( )个。
(2)当m=10时,今天卖出足球( )个。
(2)当m=( )时,今天卖出足球60个。
昨天卖出48个足球,今天比昨天多 卖出m个。
昨天卖出的个数
48+m
58
12
依题意48+m=60,所以m=60-48。
4.
今天卖出的个数
多卖的个数
+
=
5. 省略乘号写出下面各式。
2.
a×x x×x b×8 b×1
=ax
=x2
=8b
=b
x 表示什么意思?和2x有什么区别?
不一样,x 表示的是两个x相乘;而2x表示的是两个x相加。
6. 把结果相等的两个式子连起来。
a2
2.5×2.5
x·x
62
x2
6×2
2.52
a×2
一般情况下,一个数的平方和它的2倍是不相等的。只有当这个数等于0或2时,它们才相等。
7. 根据运算定律在 里填上适当的数或字母。
a+(2+c)=( + )+
a b 4= ( )
3x+5x=( + )
4×(x+3)= × + ×
a
2
c
a
b
4
3
5
x
4
x
4
3
运算定律要记牢,字母和数一样看。
8.
在 中填上适当的字母或数。
+b= +3
x× =2.6×
25×a+b× =( + )×25
b
3
x
2.6
25
a
b
这里运用了哪些运算定律?
加法交换律
乘法交换律
乘法分配律
s = vt = 260×30=7800(米)
(1)用v表示速度,t表示时间,s表示路程。
s =_______
(2)如果每分钟行260m,时间是30分,路
程是多少米?
我每分钟骑v m。
2分钟骑______m,
t分钟骑______m。
9.
2v
vt
vt
答:路程是7800米。
路程=速度×时间
v
2
s
=
×
t
长方形的面积=长×宽
长方形的周长=(长+宽)×2
10.(1)用字母表示出长方形的面积和周长。
a
b
S=
C=
ab
2(a+b)
a
b
S
=
×
a
2
C
=
×
( )
b
+
2(a+b)
S = ab
= 8×5
= 40(cm )
C = 2(a+b)
= 2×(8+5)
= 26(cm)
答:它的面积是40cm ,周长是26cm。
注意:在计算面积与周长时,要用字母表示的公式来算,这是和以前不同的。
10.(2)一个长方形的长是 8 cm,宽是 5 cm,它的面积和周长各是多少?
11. 用 a 表示商品的单价,x 表示数量,c 表示总价,分别写出它们之间的数量关系:
c=
a=
x=
如果每袋方便面 1.50 元, 6元可以买几袋?
ax
c÷x
c÷a
x = c÷a
= 6÷1.50
= 4
答: 6元可以买4袋。
从左边选一个公式解决下面的问题。
12.
工作效率 (个/分) 工作时间 分 工作总量
个
x 5
m 150
a t c=
王红每分钟打字50个,利用表中的公式计算她1小时打多少个字。
5x
150÷m
at
c=at
=50×60
=3000(个)
答:她1小时打3000个字。
根据工作效率、工作时间和工作总量的关系可以填表。
长方形的面积=长×宽
13*. 在右图中,
(1)哪一部分的面积是ac
(2)哪一部分的面积是bc
c
b
a
ac
bc
(3)整个图形的面积是多少?
长为a,宽为c,
面积是ac。
长为b,宽为c,
面积是bc。
13*.在右图中,
(1)哪一部分的面积是ac
(2)哪一部分的面积是bc
c
b
a
ac
bc
(3)整个图形的面积是多少?
用左边长方形的面积加右边长方形的面积
方法一
ac+bc
方法二
把整个图形看成是长(a+b),宽c的大长方形
(a+b)c
13*.在右图中,
(1)哪一部分的面积是ac
(2)哪一部分的面积是bc
c
b
a
ac
bc
(3)整个图形的面积是多少?
答: (1)左边长方形长方形的面积是ac。
(2)右边长方形的面积是bc。
(3)整个图形的面积是(ac+bc)或(a+b)c。
拓展提升
如图,边长为b cm的大正方形中有一个边长a cm的小正方形。
(1)图中涂色部分的面积是 cm ,周长是 cm。
a cm
b cm
(2)当a =10,b =23时,涂色部分的周长和面积分别是多少?
S涂色部分= S大正方形- S小正方形
(b -a )
4b
当a =10,b =23时,
4b=4×23=92
b -a =23 -10 =23×23-10×10=429
答:涂色部分的周长是92cm,面积别是429cm 。
C涂色部分= C大正方形
人教版数学
五年级上册
人教版数学五年级(上)
练习十二
简易方程
5
重点回顾
用字母表示数及用含有字母的式子表示数量关系时,需要注意什么?
1.含有字母的式子中乘号可以省略,数字在字母前面。
2.用含有字母的式子表示生活中的数量关系时,字母
所取的数值要符合实际情况。
3.表示同一个数量时要用同一个未知数。
4.较复杂的式子,要根据乘法分配律进行计算或化简。
如何求含有字母的式子表示学过的运算定律或公式?
加法交换律 α+b=b+α
加法结合律 α+b+c=α+(b+c)
乘法交换律 αb=bα
乘法结合律 (αb)c=α(bc)
乘法分配律 (α+b)c=αc+bc
图形 面积公式 周长公式
长方形 S=αb C=2(α+b)
正方形 S=α2 C=4α
练习巩固
(教材第55页练习十二)
-105
如果我们用字母x表示身高,那么……
我们也可以用其他字母表示身高,比如h等。
1.成年男子的标准体重通常用下面的式子表示:
用含有字母的式子表示出成年男子的标准体重。
______________________
标准体重=身高-105
身高用厘米数,体重用千克数。
x
你能用它算出你爸爸的标准体重应是多少吗?
我爸爸的身高是1米72厘米,那么他的标准体重应该是多少呢?
1.成年男子的标准体重通常用下面的式子表示:
用含有字母的式子表示出成年男子的标准体重。
______________________
标准体重=身高-105
x-105
身高用厘米数,体重用千克数。
x-105=172-105=67(kg)
1米72厘米=172厘米
答:爸爸的标准体重应该是67kg。
我爸体重是80kg,那该减肥啦!
1.成年男子的标准体重通常用下面的式子表示:
用含有字母的式子表示出成年男子的标准体重。
______________________
标准体重=身高-105
x-105
身高用厘米数,体重用千克数。
你能用它算出你爸爸的标准体重应是多少吗?
2.
原来有n元。
现在有 元。
(n+3)
车上原来有x人。
现在有 人。
(x 5)
原来n元,现在又放入3元,即在n元基础上又多了3元。
原来车上有x人,现在下车5人,即少了5人。
有m个饺子(m 为整十数), 每盘装10个。可以装 盘。
每袋有a条鱼,
一共有 条。
m÷10
3a
求3个a是多少用乘法计算。
求m里面有多少个10用除法计算。
2.
3.(1)我国青少年(7~17 岁)在1980年平均身高x cm,到2000年,平均身高增长了6cm。
(x+6)
2000年我国青少年平均身高 cm。
1980年的平均身高 + 6 = 2000年的平均身高
x
+ 6
3.(1)
0.18a
装上翅膀,怎么也飞不起来?
你们的骨骼太重!
鸟的骨骼约是体重的0.05~0.06倍,人的骨骼约是体重
的0.18倍。一个人重a kg,骨骼约是 kg。
3.(2)
早上身高 - 2 =晚上身高
人的身高早晚可能会相差2cm,在早上最高,晚上最矮。一个人早 上身高 bcm,晚上身高可能是 cm。
(b-2)
依题意,人晚上身高比早上身高少2厘米。
b
- 2
真的是这样吗?那我现在的身高132厘米,早上应高一点,而晚上就要矮一点啰。
3.(3)
小英家本月的用电量是80千瓦时,交电费c元,那么电费每千瓦时是 元。
c÷ 80
单价=总价÷数量
我明白了:用字母表示数量关系时,可以把字母看作普通的数来进行思考。
总价
求单价
数量
3.(4)
(1)今天卖出足球( )个。
(2)当m=10时,今天卖出足球( )个。
(2)当m=( )时,今天卖出足球60个。
昨天卖出48个足球,今天比昨天多 卖出m个。
昨天卖出的个数
48+m
58
12
依题意48+m=60,所以m=60-48。
4.
今天卖出的个数
多卖的个数
+
=
5. 省略乘号写出下面各式。
2.
a×x x×x b×8 b×1
=ax
=x2
=8b
=b
x 表示什么意思?和2x有什么区别?
不一样,x 表示的是两个x相乘;而2x表示的是两个x相加。
6. 把结果相等的两个式子连起来。
a2
2.5×2.5
x·x
62
x2
6×2
2.52
a×2
一般情况下,一个数的平方和它的2倍是不相等的。只有当这个数等于0或2时,它们才相等。
7. 根据运算定律在 里填上适当的数或字母。
a+(2+c)=( + )+
a b 4= ( )
3x+5x=( + )
4×(x+3)= × + ×
a
2
c
a
b
4
3
5
x
4
x
4
3
运算定律要记牢,字母和数一样看。
8.
在 中填上适当的字母或数。
+b= +3
x× =2.6×
25×a+b× =( + )×25
b
3
x
2.6
25
a
b
这里运用了哪些运算定律?
加法交换律
乘法交换律
乘法分配律
s = vt = 260×30=7800(米)
(1)用v表示速度,t表示时间,s表示路程。
s =_______
(2)如果每分钟行260m,时间是30分,路
程是多少米?
我每分钟骑v m。
2分钟骑______m,
t分钟骑______m。
9.
2v
vt
vt
答:路程是7800米。
路程=速度×时间
v
2
s
=
×
t
长方形的面积=长×宽
长方形的周长=(长+宽)×2
10.(1)用字母表示出长方形的面积和周长。
a
b
S=
C=
ab
2(a+b)
a
b
S
=
×
a
2
C
=
×
( )
b
+
2(a+b)
S = ab
= 8×5
= 40(cm )
C = 2(a+b)
= 2×(8+5)
= 26(cm)
答:它的面积是40cm ,周长是26cm。
注意:在计算面积与周长时,要用字母表示的公式来算,这是和以前不同的。
10.(2)一个长方形的长是 8 cm,宽是 5 cm,它的面积和周长各是多少?
11. 用 a 表示商品的单价,x 表示数量,c 表示总价,分别写出它们之间的数量关系:
c=
a=
x=
如果每袋方便面 1.50 元, 6元可以买几袋?
ax
c÷x
c÷a
x = c÷a
= 6÷1.50
= 4
答: 6元可以买4袋。
从左边选一个公式解决下面的问题。
12.
工作效率 (个/分) 工作时间 分 工作总量
个
x 5
m 150
a t c=
王红每分钟打字50个,利用表中的公式计算她1小时打多少个字。
5x
150÷m
at
c=at
=50×60
=3000(个)
答:她1小时打3000个字。
根据工作效率、工作时间和工作总量的关系可以填表。
长方形的面积=长×宽
13*. 在右图中,
(1)哪一部分的面积是ac
(2)哪一部分的面积是bc
c
b
a
ac
bc
(3)整个图形的面积是多少?
长为a,宽为c,
面积是ac。
长为b,宽为c,
面积是bc。
13*.在右图中,
(1)哪一部分的面积是ac
(2)哪一部分的面积是bc
c
b
a
ac
bc
(3)整个图形的面积是多少?
用左边长方形的面积加右边长方形的面积
方法一
ac+bc
方法二
把整个图形看成是长(a+b),宽c的大长方形
(a+b)c
13*.在右图中,
(1)哪一部分的面积是ac
(2)哪一部分的面积是bc
c
b
a
ac
bc
(3)整个图形的面积是多少?
答: (1)左边长方形长方形的面积是ac。
(2)右边长方形的面积是bc。
(3)整个图形的面积是(ac+bc)或(a+b)c。
拓展提升
如图,边长为b cm的大正方形中有一个边长a cm的小正方形。
(1)图中涂色部分的面积是 cm ,周长是 cm。
a cm
b cm
(2)当a =10,b =23时,涂色部分的周长和面积分别是多少?
S涂色部分= S大正方形- S小正方形
(b -a )
4b
当a =10,b =23时,
4b=4×23=92
b -a =23 -10 =23×23-10×10=429
答:涂色部分的周长是92cm,面积别是429cm 。
C涂色部分= C大正方形
