人教版五年级上册数学5 .2.4.3实际问题与方程(3)课件(28张PPT)
文档属性
| 名称 | 人教版五年级上册数学5 .2.4.3实际问题与方程(3)课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 09:46:17 | ||
图片预览






文档简介
(共28张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
第10课时 实际问题与方程(3)
简易方程
5
1. 理解有关两数之积的数量关系,掌握根据具体情境列出形如a(x±b)=c的方程来解决实际问题。
2. 经历利用迁移类推的方法去解决实际问题的过程,培养方程意识和解决问题的策略方法。
3. 在解方程过程中培养思维能力,感受数学学习的乐趣,树立学习数学的信心。
学习目标
【重点】
分析数量关系,会列出含有括号的方
程并解答。
【难点】
列方程解答类似两积之和或差的问题。
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
课堂导入
填一填,说一说。
工作效率×工作时间 =( )
单价×数量= ( )
速度×时间 = ( )
总价
路程
工作总量
这些常用的数量关系和公式都可以作为等量关系式来列方程。
总价÷单价=数量
总价÷数量=单价
路程÷速度=时间
路程÷时间=速度
新知探究
3
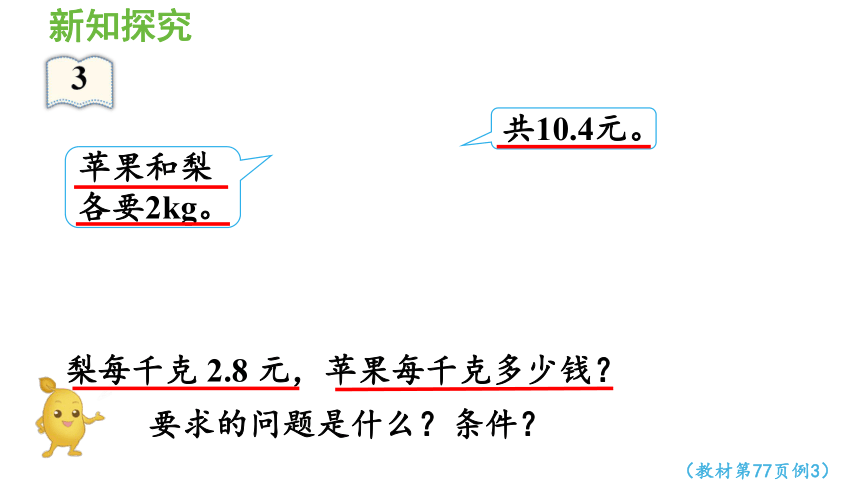
(教材第77页例3)
共10.4元。
苹果和梨各要2kg。
从图中你获取了哪些条件?
梨每千克 2.8 元,苹果每千克多少钱?
要求的问题是什么?
小组讨论:如何列方程解答这道题呢?
合作要求
1.阅读课本相关内容,各人先尝试解题。
2.组内交流,说说自己的解题思路。
3.比较不同的解法,准备全班汇报。
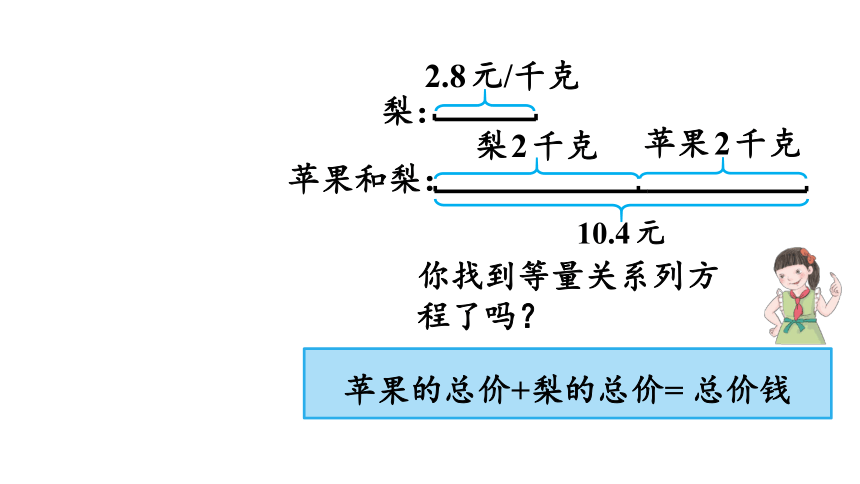
苹果和梨:
梨:
10.4元
2.8元/千克
梨2千克
苹果2千克
你找到等量关系列方程了吗?
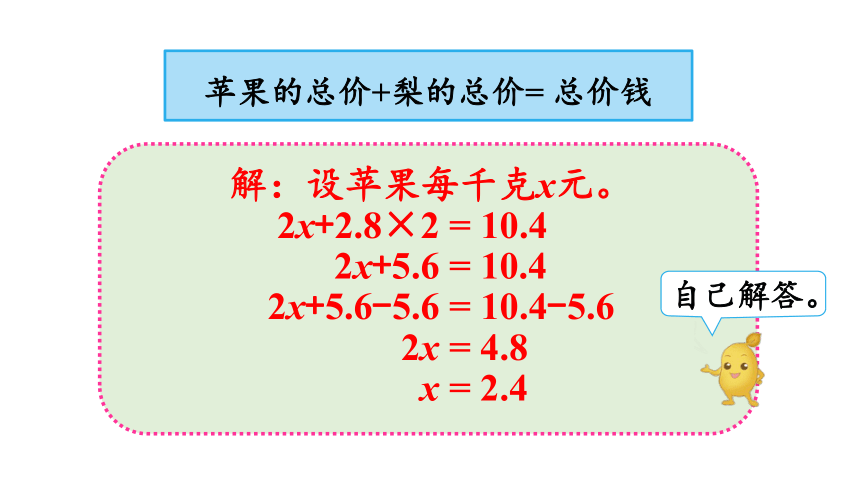
苹果的总价+梨的总价= 总价钱
苹果的总价+梨的总价= 总价钱
解:设苹果每千克x元。
2x+2.8×2 = 10.4
2x+5.6 = 10.4
2x+5.6-5.6 = 10.4-5.6
2x = 4.8
x = 2.4
自己解答。
(1)经检验,列的方程正确;
(2)把x = 2.4代入方程,
方程左边= 2x+2.8×2
=2×2.4+2.8×2
=10.4=方程右边
所以,x=2.4是方程的解。
检验
解方程后要记得检验结果后再作答。
答:苹果每千克2.4元。
解:设苹果每千克x元。
x = 2.4
2.8+x = 5.2
(2.8+x)×2÷2 = 10.4÷2
两种水果的单价总和 ×2= 总钱数
2.8+x-2.8 = 5.2-2.8
(2.8+x)×2 = 10.4
把什么看作一个整体?
还可以怎样列方程呢?
(1)经检验,列的方程正确;
(2)把x = 2.4代入方程,
方程左边=(x+2.8)×2
=(2.4+2.8)×2
=10.4=方程右边
所以,x=2.4是方程的解。
检验
答:苹果每千克2.4元。
没有检验要求时,可以口算检验。
大家一起讨论:这两种解法有什么联系?
苹果的总价+梨的总价= 总价钱
解:设苹果每千克x元。
2x+2.8×2 = 10.4
2x+5.6 = 10.4
2x+5.6-5.6 = 10.4-5.6
2x = 4.8
x = 2.4
答:苹果每千克2.4元。
两种水果的单价总和 ×2= 总钱数
解:设苹果每千克x元。
(2.8+x)×2 = 10.4
(2.8+x)×2÷2 = 10.4÷2
2.8+x = 5.2
2.8+x-2.8 = 5.2-2.8
x = 2.4
答:苹果每千克2.4元。
应用了乘法分配律
课堂练习
做一做
1.
从图中我们能获得哪些条件?
(教材第77页“做一做”)
4张门票共花了11元。
成人票每张4元。
儿童票每张多少钱?
两张成人票和两张儿童票共11元。
所求问题是什么?
成人票的总价+儿童票的总价=11元
成人票的总价+儿童票的总价=11元
2x+2×4=11
2x+8=11
2x+8 8=11 8
2x=3
2x÷2=3÷2
x=1.5
解:设儿童票每张x元。
答:儿童票每张1.5元。
两种门票的单价总和 ×2= 11元
(x+4)×2=11
(x+4)×2÷2=11÷2
x+4=5.5
x+4-4=5.5-4
x=1.5
解:设儿童票每张x元。
答:儿童票每张1.5元。
还可以怎样列方程呢?
解:设饮料瓶有x个。
(6+x)×0.12 = 1.8
(6+x)×0.12÷0.12 = 1.8÷0.12
6+x = 15
x = 9
答:饮料瓶有9个。
饮料瓶有几个?
2.
(教材第80页第2题)
我们收集了易拉罐和饮料瓶,易拉罐有6个。
每个都是0.12元,一共卖了1.8元。
(易拉罐的个数+饮料瓶的个数)×0.12=1.8
(教材第80页第4题)
《科学家》丛书有4本,《发明家》丛书有多少本?
3.
关键句
《科学家》丛书总价+《发明家》丛书总价=22元
2.5元/本
我买了两套丛书,共花了22元。
4元/本
我买了两套丛书,共花了22元。
解:设《发明家》丛书有x本。
2.5×4+4x = 22
10+4x = 22
10+4x-10 = 22-10
x = 3
答:《发明家》丛书有3本。
3.
我买了两套丛书,共花了22元。
4元/本
2.5元/本
《科学家》丛书有4本,《发明家》丛书有多少本?
4. 店里运来150箱汽水,张叔叔每次运30箱,已经运了2次,剩下的还要几次可以运完?
已经运走的箱数+剩下的箱数=总箱数
解:设剩下的还要x次可以运完。
30×2+30x = 150
60+30x = 150
30x = 90
x = 3
答:剩下的还要3次运完。
(教材第80页第3题)
2号楼第二季度水费收取表
单价:2.5元/吨
小朋友,你会看水表吗?
水表上的读数表示水表安装以后的用水总吨数,两次读数的差就是这段时间里的用水吨数。
3102
1.
102室本次的水表读数是多少?
提升练习
室号 上次读数/吨 本次读数/吨 水费/元
101 2756 2788 80
102 3102 135
(本次读数-上次读数)×单价=水费
2号楼第二季度水费收取表
单价:2.5元/吨
室号 上次读数/吨 本次读数/吨 水费/元
101 2756 2788 80
102 3102 135
102室第二季度用水吨数×单价=水费
本次读数
上次读数
-
解:设102室本次水表读数是x。
(x-3102)×2.5 = 135
(x-3102)×2.5÷2.5 = 135÷2.5
x-3102 = 54
x-3102+3102 = 54+3102
x = 3156
答:102室本次水表读数是3156。
(本次读数-上次读数)×单价=水费
2. 师徒二人共同生产一批零件,4天完成。徒弟每天生产48个零件,一共比师傅少生产48个零件。师傅每天、生产多少个零件?
师傅生产的总个数-徒弟生产的总个数=48个
解:设师傅每天生产x个零件。
4x- 48×4= 48
4x-192= 48
4x-192+192= 48+192
4x = 240
x = 60
答:师傅每天生产60个零件。
徒弟比师傅每天少生产的个数×4=48个
解:设师傅每天生产x个零件。
(x-48)×4 = 48
(x-48)×4÷4 = 48÷4
x-48 = 12
x-48+48 = 12+48
x = 60
这题的两种解法也是乘法分配律的推广。
答:师傅每天生产60个零件。
还可以怎样列方程呢?
课堂小结
这节课你有什么收获?
1.列方程解决实际问题关键是找等量关系,找等量关
系时尽量顺向思维。
2.解有括号的方程可以先用运算定律转化,也可以直
接解。解方程后要检验结果。
3.运用乘法分配律可以列出不同的方程来解决实际问
题。
人教版数学
五年级上册
人教版数学五年级(上)
第10课时 实际问题与方程(3)
简易方程
5
1. 理解有关两数之积的数量关系,掌握根据具体情境列出形如a(x±b)=c的方程来解决实际问题。
2. 经历利用迁移类推的方法去解决实际问题的过程,培养方程意识和解决问题的策略方法。
3. 在解方程过程中培养思维能力,感受数学学习的乐趣,树立学习数学的信心。
学习目标
【重点】
分析数量关系,会列出含有括号的方
程并解答。
【难点】
列方程解答类似两积之和或差的问题。
工作总量÷工作效率=工作时间
工作总量÷工作时间=工作效率
课堂导入
填一填,说一说。
工作效率×工作时间 =( )
单价×数量= ( )
速度×时间 = ( )
总价
路程
工作总量
这些常用的数量关系和公式都可以作为等量关系式来列方程。
总价÷单价=数量
总价÷数量=单价
路程÷速度=时间
路程÷时间=速度
新知探究
3
(教材第77页例3)
共10.4元。
苹果和梨各要2kg。
从图中你获取了哪些条件?
梨每千克 2.8 元,苹果每千克多少钱?
要求的问题是什么?
小组讨论:如何列方程解答这道题呢?
合作要求
1.阅读课本相关内容,各人先尝试解题。
2.组内交流,说说自己的解题思路。
3.比较不同的解法,准备全班汇报。
苹果和梨:
梨:
10.4元
2.8元/千克
梨2千克
苹果2千克
你找到等量关系列方程了吗?
苹果的总价+梨的总价= 总价钱
苹果的总价+梨的总价= 总价钱
解:设苹果每千克x元。
2x+2.8×2 = 10.4
2x+5.6 = 10.4
2x+5.6-5.6 = 10.4-5.6
2x = 4.8
x = 2.4
自己解答。
(1)经检验,列的方程正确;
(2)把x = 2.4代入方程,
方程左边= 2x+2.8×2
=2×2.4+2.8×2
=10.4=方程右边
所以,x=2.4是方程的解。
检验
解方程后要记得检验结果后再作答。
答:苹果每千克2.4元。
解:设苹果每千克x元。
x = 2.4
2.8+x = 5.2
(2.8+x)×2÷2 = 10.4÷2
两种水果的单价总和 ×2= 总钱数
2.8+x-2.8 = 5.2-2.8
(2.8+x)×2 = 10.4
把什么看作一个整体?
还可以怎样列方程呢?
(1)经检验,列的方程正确;
(2)把x = 2.4代入方程,
方程左边=(x+2.8)×2
=(2.4+2.8)×2
=10.4=方程右边
所以,x=2.4是方程的解。
检验
答:苹果每千克2.4元。
没有检验要求时,可以口算检验。
大家一起讨论:这两种解法有什么联系?
苹果的总价+梨的总价= 总价钱
解:设苹果每千克x元。
2x+2.8×2 = 10.4
2x+5.6 = 10.4
2x+5.6-5.6 = 10.4-5.6
2x = 4.8
x = 2.4
答:苹果每千克2.4元。
两种水果的单价总和 ×2= 总钱数
解:设苹果每千克x元。
(2.8+x)×2 = 10.4
(2.8+x)×2÷2 = 10.4÷2
2.8+x = 5.2
2.8+x-2.8 = 5.2-2.8
x = 2.4
答:苹果每千克2.4元。
应用了乘法分配律
课堂练习
做一做
1.
从图中我们能获得哪些条件?
(教材第77页“做一做”)
4张门票共花了11元。
成人票每张4元。
儿童票每张多少钱?
两张成人票和两张儿童票共11元。
所求问题是什么?
成人票的总价+儿童票的总价=11元
成人票的总价+儿童票的总价=11元
2x+2×4=11
2x+8=11
2x+8 8=11 8
2x=3
2x÷2=3÷2
x=1.5
解:设儿童票每张x元。
答:儿童票每张1.5元。
两种门票的单价总和 ×2= 11元
(x+4)×2=11
(x+4)×2÷2=11÷2
x+4=5.5
x+4-4=5.5-4
x=1.5
解:设儿童票每张x元。
答:儿童票每张1.5元。
还可以怎样列方程呢?
解:设饮料瓶有x个。
(6+x)×0.12 = 1.8
(6+x)×0.12÷0.12 = 1.8÷0.12
6+x = 15
x = 9
答:饮料瓶有9个。
饮料瓶有几个?
2.
(教材第80页第2题)
我们收集了易拉罐和饮料瓶,易拉罐有6个。
每个都是0.12元,一共卖了1.8元。
(易拉罐的个数+饮料瓶的个数)×0.12=1.8
(教材第80页第4题)
《科学家》丛书有4本,《发明家》丛书有多少本?
3.
关键句
《科学家》丛书总价+《发明家》丛书总价=22元
2.5元/本
我买了两套丛书,共花了22元。
4元/本
我买了两套丛书,共花了22元。
解:设《发明家》丛书有x本。
2.5×4+4x = 22
10+4x = 22
10+4x-10 = 22-10
x = 3
答:《发明家》丛书有3本。
3.
我买了两套丛书,共花了22元。
4元/本
2.5元/本
《科学家》丛书有4本,《发明家》丛书有多少本?
4. 店里运来150箱汽水,张叔叔每次运30箱,已经运了2次,剩下的还要几次可以运完?
已经运走的箱数+剩下的箱数=总箱数
解:设剩下的还要x次可以运完。
30×2+30x = 150
60+30x = 150
30x = 90
x = 3
答:剩下的还要3次运完。
(教材第80页第3题)
2号楼第二季度水费收取表
单价:2.5元/吨
小朋友,你会看水表吗?
水表上的读数表示水表安装以后的用水总吨数,两次读数的差就是这段时间里的用水吨数。
3102
1.
102室本次的水表读数是多少?
提升练习
室号 上次读数/吨 本次读数/吨 水费/元
101 2756 2788 80
102 3102 135
(本次读数-上次读数)×单价=水费
2号楼第二季度水费收取表
单价:2.5元/吨
室号 上次读数/吨 本次读数/吨 水费/元
101 2756 2788 80
102 3102 135
102室第二季度用水吨数×单价=水费
本次读数
上次读数
-
解:设102室本次水表读数是x。
(x-3102)×2.5 = 135
(x-3102)×2.5÷2.5 = 135÷2.5
x-3102 = 54
x-3102+3102 = 54+3102
x = 3156
答:102室本次水表读数是3156。
(本次读数-上次读数)×单价=水费
2. 师徒二人共同生产一批零件,4天完成。徒弟每天生产48个零件,一共比师傅少生产48个零件。师傅每天、生产多少个零件?
师傅生产的总个数-徒弟生产的总个数=48个
解:设师傅每天生产x个零件。
4x- 48×4= 48
4x-192= 48
4x-192+192= 48+192
4x = 240
x = 60
答:师傅每天生产60个零件。
徒弟比师傅每天少生产的个数×4=48个
解:设师傅每天生产x个零件。
(x-48)×4 = 48
(x-48)×4÷4 = 48÷4
x-48 = 12
x-48+48 = 12+48
x = 60
这题的两种解法也是乘法分配律的推广。
答:师傅每天生产60个零件。
还可以怎样列方程呢?
课堂小结
这节课你有什么收获?
1.列方程解决实际问题关键是找等量关系,找等量关
系时尽量顺向思维。
2.解有括号的方程可以先用运算定律转化,也可以直
接解。解方程后要检验结果。
3.运用乘法分配律可以列出不同的方程来解决实际问
题。
