人教版五年级上册数学6 多边形的面积整理和复习课件(27张PPT)
文档属性
| 名称 | 人教版五年级上册数学6 多边形的面积整理和复习课件(27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-10 11:18:38 | ||
图片预览



文档简介
(共27张PPT)
人教版数学
五年级上册
人教版数学五年级(上)
整理和复习
多边形的面积
6
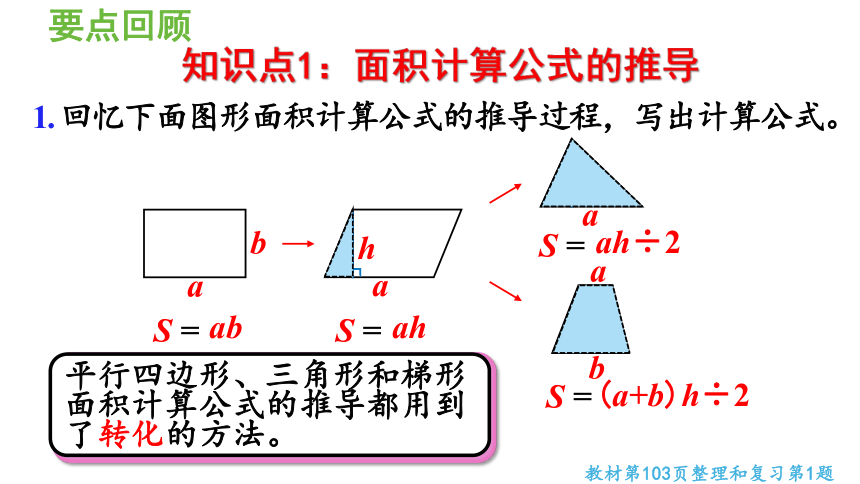
小组交流:本单元主要学习了哪些内容?
知识梳理
分割法、添补法;数格子法、转化法
S=ah
S=ah÷2
S=(a+b)h÷2
要点回顾
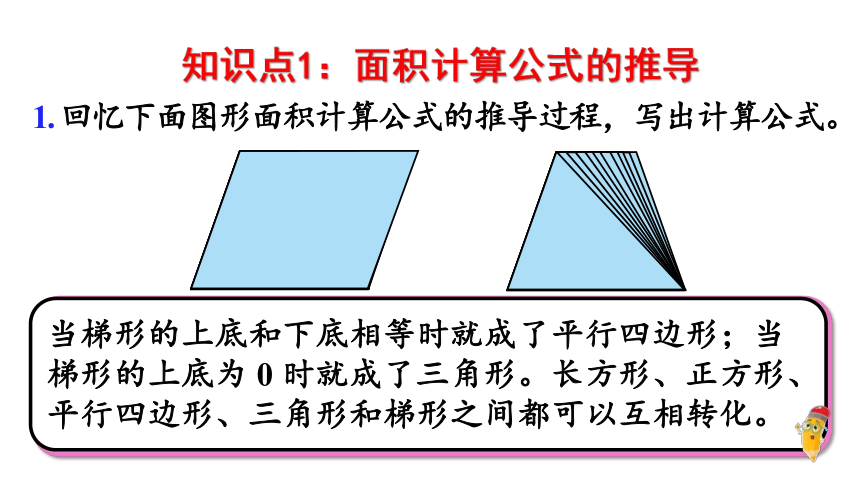
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点1:面积计算公式的推导
教材第103页整理和复习第1题
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
知识点1:面积计算公式的推导
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
当梯形的上底和下底相等时就成了平行四边形;当梯形的上底为 0 时就成了三角形。长方形、正方形、平行四边形、三角形和梯形之间都可以互相转化。
知识点2:面积的计算
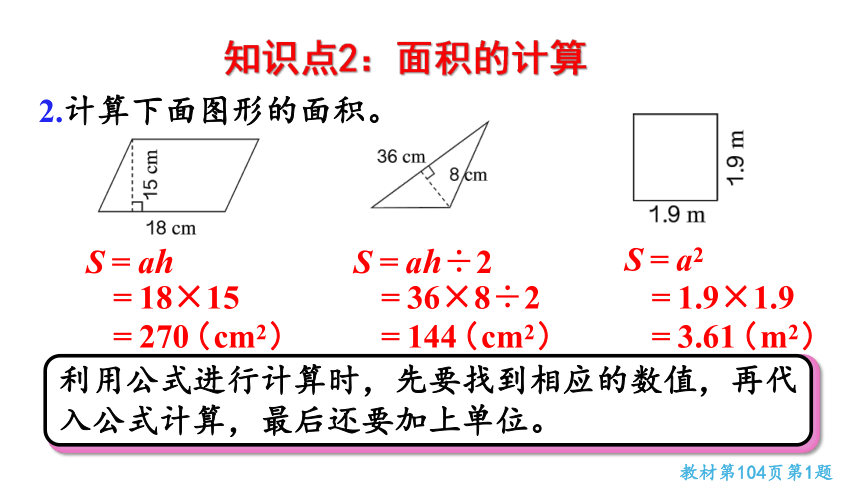
2.计算下面图形的面积。
S=ah
=270(cm2)
=18×15
S=ah÷2
=144(cm2)
=36×8÷2
S=a2
=3.61(m2)
=1.9×1.9
教材第104页第1题
利用公式进行计算时,先要找到相应的数值,再代入公式计算,最后还要加上单位。
S=ah÷2
=3.41(m2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
计算平行四边形、三角形时,还得注意底和高要相对应。
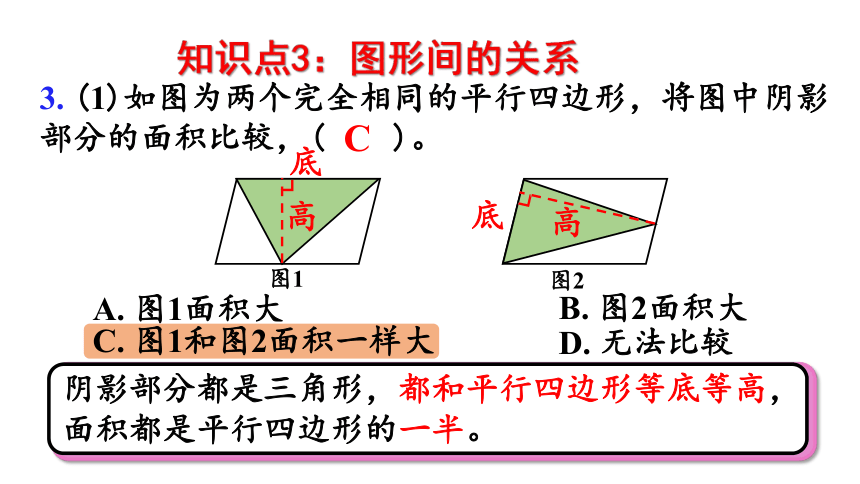
3. (1)如图为两个完全相同的平行四边形,将图中阴影部分的面积比较,( )。
A. 图1面积大
B. 图2面积大
D. 无法比较
C. 图1和图2面积一样大
底
高
底
高
C
知识点3:图形间的关系
阴影部分都是三角形,都和平行四边形等底等高,面积都是平行四边形的一半。
图2
图1
知识点3:图形间的关系
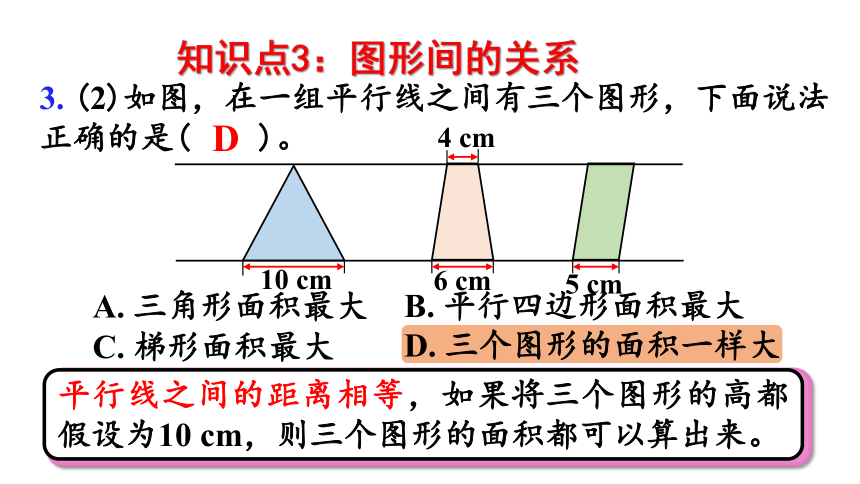
3. (2)如图,在一组平行线之间有三个图形,下面说法正确的是( )。
A. 三角形面积最大
B. 平行四边形面积最大
D. 三个图形的面积一样大
C. 梯形面积最大
10 cm
5 cm
6 cm
4 cm
D
平行线之间的距离相等,如果将三个图形的高都假设为10 cm,则三个图形的面积都可以算出来。
知识点3:图形间的关系
图形间的面积比较,往往牵涉到图形间的关系:
1.三角形的面积是与它等底等高的平行四边形面积的一半。
2.等底等高的平行四边形面积相等;
3.等底等高的三角形面积相等;
4.面积相等的平行四边形、三角形或梯形,形状不一定相同。
知识点4:组合图形的面积计算
4.计算下面图形的面积。你能想出几种方法?
S三角形=(10 5)×(12 6)÷2=15(cm2)
S长方形=12×5=60(cm2)
S=15+60=75(cm2)
教材第103页整理和复习第2题
分割成长方形和三角形
方法一
S长方形=6×5=30(cm2)
S梯形=(5+10)×(12 6)÷2=45(cm2)
S=30+45=75(cm2)
知识点4:组合图形的面积计算
分割成长方形和梯形
方法二
4.计算下面图形的面积。你能想出几种方法?
S三角形=10×(12 6)÷2
=30(cm2)
S梯形=(6+12)×5÷2
=45(cm2)
S=30+45=75(cm2)
知识点4:组合图形的面积计算
分割成三角形和梯形
方法三
4.计算下面图形的面积。你能想出几种方法?
S长方形=12×10=120(cm2)
S梯形=(6+12)×(10 5)÷2
=45(cm2)
S=120 45=75(cm2)
知识点4:组合图形的面积计算
添补成长方形
方法四
组合图形的解法往往不止一种,解题时应综合分析,尽量选用简便的方法计算。
4.计算下面图形的面积。你能想出几种方法?
知识点5:不规则图形面积的估算
5.图中每个小方格的面积是1 cm ,阴影部分的面积约是多少平方厘米?
数方格
方法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
S=28满格+28不满格÷2
=42(cm2)
答:阴影部分的面积约是42 cm2。
知识点5:不规则图形面积的估算
S三角形=ah÷2
=10×8÷2
=40(cm2)
答:阴影部分的面积约是40 cm2。
转化成三角形
方法二
5.图中每个小方格的面积是1 cm ,阴影部分的面积约是多少平方厘米?
(1)平行四边形的面积一定比梯形的面积大。 ( )
(2)平行四边形的面积等于三角形面积的2倍。 ( )
(3)梯形的上底、下底越长,面积越大。 ( )
(4)任何一个梯形都可以分成两个等高的三角形。( )
(5)两个面积相等的三角形,一定能拼成一个平行四边
形。 ( )
课堂练习
1.判断下面各题的叙述是否正确。
√
×
×
×
×
你判断的理由是什么?
2.下图是教室的一面墙。如果砌这面墙平均每平方米用砖 185 块,一共需要用多少块砖?
这面墙由一个三角形和一个长方形组成。先求面积,再求共需用砖的块数。
长方形:5×4 = 20(m2)
三角形:5×5÷2 = 3(m2)
墙:20+3 = 23(m2)
砖的块数:185×23 = 4255(块)
答:一共需要用 4255 块砖。
教材第104页第3题
3.有一台收割机,作业宽度是1.8 m。每小时行5 km,大约多少小时可以收割完下边这块地?
200 m
330 m
100 m
先求这块地的面积,然后计算出收割机的工作效率,最后算工作时间。
5 km = 5000 m
1.8×5000 = 9000(m2)
(200+330)×100÷2 = 26500(m2)
26500÷9000 ≈ 3(时)
答:大约3小时可以收割完这块地。
教材第104页第4题
4.两艘军舰同时从相距948 km的两个港口对开。一艘军舰每小时行38 km,另一艘军舰每小时行41 km。经过几小时两艘军舰相遇?
948÷(38+41)
=12(时)
=948÷79
答:经过12小时两艘军舰相遇。
这是一道相遇问题,相遇时间=总路程÷两军舰的速度之和。
教材第105页第6题
教材第105页第7题
5.下面是一个火箭模型的平面图,计算它的面积。
三角形: 8×10÷2 = 40(cm )
长方形:70×8 = 560(cm )
梯形:(8+16)×8÷2 = 96(cm )
平面图:40+560+96 = 696(cm )
答:这个平面图的面积是 696 cm 。
这个平面图可分成一个三角形、一个长方形和一个梯形。
6*.图中小方格的边长是1 m,请你估计涂色部分的面积。
=26+42÷2
=47(m2)
=26+21
答:涂色部分的面积大约是47m2 。
本题可采用数方格的方法进行估计。
S=S全格+S半格
教材第105页第8*题
梯形:(4+8)×9÷2 = 54(m2)
涂色部分:54 - 8 = 46(m2)
长方形:4×2 = 8(m2)
答:涂色部分的面积大约是46 m2 。
也可把涂色部分看作中间挖去一个长方形的梯形。
6*.图中小方格的边长是1 m,请你估计涂色部分的面积。
①
②
③
④
⑤
⑥
⑦
7.这个由一副七巧板拼出的正方形边长为12 cm,你能求出每个图形的面积吗?
教材第103页整理和复习思考题
①②各占正方形的四分之一;④⑤⑦各占八分之一;③⑥各占十六分之一。先求正方形的面积,再求各部分的面积。
①②:
12×12÷4=36(cm2)
④⑤⑦:
12×12÷8=18(cm2)
③⑥:
12×12÷16 =9(cm2)
①
②
③
④
⑤
⑥
⑦
7.这个由一副七巧板拼出的正方形边长为12 cm,你能求出每个图形的面积吗?
人教版数学
五年级上册
人教版数学五年级(上)
整理和复习
多边形的面积
6
小组交流:本单元主要学习了哪些内容?
知识梳理
分割法、添补法;数格子法、转化法
S=ah
S=ah÷2
S=(a+b)h÷2
要点回顾
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点1:面积计算公式的推导
教材第103页整理和复习第1题
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
知识点1:面积计算公式的推导
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
当梯形的上底和下底相等时就成了平行四边形;当梯形的上底为 0 时就成了三角形。长方形、正方形、平行四边形、三角形和梯形之间都可以互相转化。
知识点2:面积的计算
2.计算下面图形的面积。
S=ah
=270(cm2)
=18×15
S=ah÷2
=144(cm2)
=36×8÷2
S=a2
=3.61(m2)
=1.9×1.9
教材第104页第1题
利用公式进行计算时,先要找到相应的数值,再代入公式计算,最后还要加上单位。
S=ah÷2
=3.41(m2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
计算平行四边形、三角形时,还得注意底和高要相对应。
3. (1)如图为两个完全相同的平行四边形,将图中阴影部分的面积比较,( )。
A. 图1面积大
B. 图2面积大
D. 无法比较
C. 图1和图2面积一样大
底
高
底
高
C
知识点3:图形间的关系
阴影部分都是三角形,都和平行四边形等底等高,面积都是平行四边形的一半。
图2
图1
知识点3:图形间的关系
3. (2)如图,在一组平行线之间有三个图形,下面说法正确的是( )。
A. 三角形面积最大
B. 平行四边形面积最大
D. 三个图形的面积一样大
C. 梯形面积最大
10 cm
5 cm
6 cm
4 cm
D
平行线之间的距离相等,如果将三个图形的高都假设为10 cm,则三个图形的面积都可以算出来。
知识点3:图形间的关系
图形间的面积比较,往往牵涉到图形间的关系:
1.三角形的面积是与它等底等高的平行四边形面积的一半。
2.等底等高的平行四边形面积相等;
3.等底等高的三角形面积相等;
4.面积相等的平行四边形、三角形或梯形,形状不一定相同。
知识点4:组合图形的面积计算
4.计算下面图形的面积。你能想出几种方法?
S三角形=(10 5)×(12 6)÷2=15(cm2)
S长方形=12×5=60(cm2)
S=15+60=75(cm2)
教材第103页整理和复习第2题
分割成长方形和三角形
方法一
S长方形=6×5=30(cm2)
S梯形=(5+10)×(12 6)÷2=45(cm2)
S=30+45=75(cm2)
知识点4:组合图形的面积计算
分割成长方形和梯形
方法二
4.计算下面图形的面积。你能想出几种方法?
S三角形=10×(12 6)÷2
=30(cm2)
S梯形=(6+12)×5÷2
=45(cm2)
S=30+45=75(cm2)
知识点4:组合图形的面积计算
分割成三角形和梯形
方法三
4.计算下面图形的面积。你能想出几种方法?
S长方形=12×10=120(cm2)
S梯形=(6+12)×(10 5)÷2
=45(cm2)
S=120 45=75(cm2)
知识点4:组合图形的面积计算
添补成长方形
方法四
组合图形的解法往往不止一种,解题时应综合分析,尽量选用简便的方法计算。
4.计算下面图形的面积。你能想出几种方法?
知识点5:不规则图形面积的估算
5.图中每个小方格的面积是1 cm ,阴影部分的面积约是多少平方厘米?
数方格
方法一
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
S=28满格+28不满格÷2
=42(cm2)
答:阴影部分的面积约是42 cm2。
知识点5:不规则图形面积的估算
S三角形=ah÷2
=10×8÷2
=40(cm2)
答:阴影部分的面积约是40 cm2。
转化成三角形
方法二
5.图中每个小方格的面积是1 cm ,阴影部分的面积约是多少平方厘米?
(1)平行四边形的面积一定比梯形的面积大。 ( )
(2)平行四边形的面积等于三角形面积的2倍。 ( )
(3)梯形的上底、下底越长,面积越大。 ( )
(4)任何一个梯形都可以分成两个等高的三角形。( )
(5)两个面积相等的三角形,一定能拼成一个平行四边
形。 ( )
课堂练习
1.判断下面各题的叙述是否正确。
√
×
×
×
×
你判断的理由是什么?
2.下图是教室的一面墙。如果砌这面墙平均每平方米用砖 185 块,一共需要用多少块砖?
这面墙由一个三角形和一个长方形组成。先求面积,再求共需用砖的块数。
长方形:5×4 = 20(m2)
三角形:5×5÷2 = 3(m2)
墙:20+3 = 23(m2)
砖的块数:185×23 = 4255(块)
答:一共需要用 4255 块砖。
教材第104页第3题
3.有一台收割机,作业宽度是1.8 m。每小时行5 km,大约多少小时可以收割完下边这块地?
200 m
330 m
100 m
先求这块地的面积,然后计算出收割机的工作效率,最后算工作时间。
5 km = 5000 m
1.8×5000 = 9000(m2)
(200+330)×100÷2 = 26500(m2)
26500÷9000 ≈ 3(时)
答:大约3小时可以收割完这块地。
教材第104页第4题
4.两艘军舰同时从相距948 km的两个港口对开。一艘军舰每小时行38 km,另一艘军舰每小时行41 km。经过几小时两艘军舰相遇?
948÷(38+41)
=12(时)
=948÷79
答:经过12小时两艘军舰相遇。
这是一道相遇问题,相遇时间=总路程÷两军舰的速度之和。
教材第105页第6题
教材第105页第7题
5.下面是一个火箭模型的平面图,计算它的面积。
三角形: 8×10÷2 = 40(cm )
长方形:70×8 = 560(cm )
梯形:(8+16)×8÷2 = 96(cm )
平面图:40+560+96 = 696(cm )
答:这个平面图的面积是 696 cm 。
这个平面图可分成一个三角形、一个长方形和一个梯形。
6*.图中小方格的边长是1 m,请你估计涂色部分的面积。
=26+42÷2
=47(m2)
=26+21
答:涂色部分的面积大约是47m2 。
本题可采用数方格的方法进行估计。
S=S全格+S半格
教材第105页第8*题
梯形:(4+8)×9÷2 = 54(m2)
涂色部分:54 - 8 = 46(m2)
长方形:4×2 = 8(m2)
答:涂色部分的面积大约是46 m2 。
也可把涂色部分看作中间挖去一个长方形的梯形。
6*.图中小方格的边长是1 m,请你估计涂色部分的面积。
①
②
③
④
⑤
⑥
⑦
7.这个由一副七巧板拼出的正方形边长为12 cm,你能求出每个图形的面积吗?
教材第103页整理和复习思考题
①②各占正方形的四分之一;④⑤⑦各占八分之一;③⑥各占十六分之一。先求正方形的面积,再求各部分的面积。
①②:
12×12÷4=36(cm2)
④⑤⑦:
12×12÷8=18(cm2)
③⑥:
12×12÷16 =9(cm2)
①
②
③
④
⑤
⑥
⑦
7.这个由一副七巧板拼出的正方形边长为12 cm,你能求出每个图形的面积吗?
