2012届中考数学解直角三角形及其应用专题复习
图片预览


文档简介
(备战中考)中考数学深度复习讲义
(教案+中考真题+模拟试题+单元测试)
解直角三角形及其应用
◆考点聚焦
1.掌握并灵活应用各种关系解直角三角形,这是本节重点.
2.了解测量中的概念,并能灵活应用相关知识解决某些实际问题,而在将实际问题转化为直角三角形问题时,怎样合理构造直角三角形以及如何正确选用直角三角形的边角关系是本节难点,也是中考的热点.
◆备考兵法
正确地建立解直角三角形的数学模型以及熟悉测量,航海,航空,工程等实际问题中的常用概念是解决这类问题的关键.
注意:(1)准确理解几个概念:①仰角,俯角;②坡角;③坡度;④方位角.
(2)将实际问题抽象为数学问题的关键是画出符合题意的图形.
(3)在一些问题中要根据需要添加辅助线,构造出直角三角形,从而转化为解直角三角形的问题.
◆识记巩固
1.直角三角形的边角关系:
在Rt△ABC中,∠C=90°,a,b,c分别是△ABC中∠A,∠B,∠C的对边.
(1)三边之间的关系:a2+b2=_____;
(2)两锐角之间的关系:∠A+∠B=______;
(3)直角三角形斜边上的中线等于_______;
(4)在直角三角形中,30°角所对的边等于_______.
2.解直角三角形的四种类型:
已知条件 解法
两条直角边a、b c=______,tanA=______,∠B=_______.
一条直角边a和斜边c b=______,sinA=_____,∠B=______.
一条直角边a和锐角A c=_______,b=_______,∠B=_______
斜边c和锐角A a=_______,b=_______,∠B=_______
3.坡面的_________的比叫坡度i(也叫坡比),坡度越大,坡面越陡;坡面与______的夹角,用a表示,tana=i=.
4.视线在水平线上方的角叫做_______;视线在水平线下方的角叫________.
5.方向角:正北或正南方向与目标方向线所成的_______的角叫方向角,常用“北偏东(西)××度”或“南偏东(西)××度”来描述.
识记巩固参考答案:
1.(1)c2 (2)90° (3)斜边的一半 (4)斜边的一半
2. 90°-∠A 90°-∠A
90°-∠A c·sinA 90°-∠A
3.垂直高度h和水平宽度L 水平面
4.仰角 俯角
5.小于90°
◆典例精析
例1 (2011山东威海,23,10分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠E=45°,∠A=60°,AC=10,试求CD的长.
【答案】 解:过点B作BM⊥FD于点M.
在△ACB中,∠ACB=90°, ∠A=60°,AC=10,
∴∠ABC=30°, BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=30°.
∴
在△EFD中,∠F=90°, ∠E=45°,
∴∠EDF=45°,
∴.
∴.
例2 (2011山东烟台,21,8分)综合实践课上,小明所在小组要测量护城河的宽度。如图所示是护城河的一段,两岸ABCD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)
【答案】解:过点F作FG∥EM交CD于G.
则MG=EF=20米.
∠FGN=∠α=36°.
∴∠GFN=∠β-∠FGN=72°-36°=36°.
∴∠FGN=∠GFN,
∴FN=GN=50-20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin72°=30×0.95≈29(米).
一、选择题
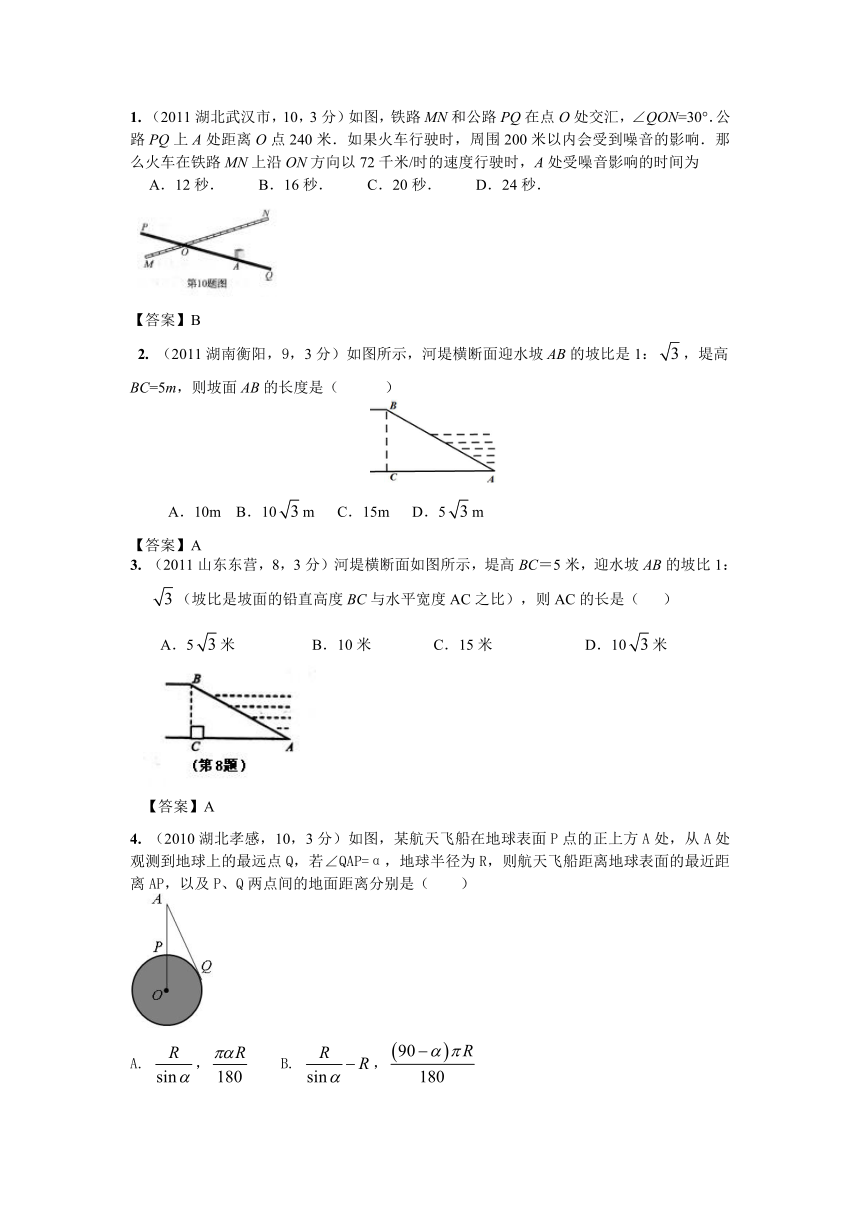
1. (2011湖北武汉市,10,3分)如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为
A.12秒. B.16秒. C.20秒. D.24秒.
【答案】B
2. (2011湖南衡阳,9,3分)如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长度是( )
A.10m B.10m C.15m D.5m
【答案】A
3. (2011山东东营,8,3分)河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比1:(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.5米 B.10米 C.15米 D.10米
【答案】A
4. (2010湖北孝感,10,3分)如图,某航天飞船在地球表面P点的正上方A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞船距离地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
A. , B. ,
C. , D. ,
【答案】B
5. (2011宁波市,9,3分)如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长l为
A. B. C. D. h·sina
【答案】A
6. (2011台湾台北,34)图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分
A. B. C.18 D.19
【答案】D
7. (2011山东潍坊,10,3分)身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
同学 甲 乙 丙 丁
放出风筝线长 140m 100m 95m 90m
线与地面夹角 30° 45° 45° 60°
A.甲 B.乙 C.丙 D.丁
【答案】D
8. (2011四川绵阳10,3)周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米。假设她们的眼睛离头顶都为10cm,则 可计算出塔高约为(结果精确到0.01,参考数据:=1.414,=1.73)
A.36.21 米 B.37. 71 米
C.40. 98 米 D.42.48 米
【答案】D
二、填空题
1. (2011山东济宁,15,3分)如图,是一张宽的矩形台球桌,一球从点(点在长边上)出发沿虚线射向边,然后反弹到边上的点. 如果,.那么点与点的距离为 .
【答案】
2. (2011浙江衢州,13,4分)在一次夏令营活动中,小明同学从营地出发,要到地的北偏东60°方向的处,他先沿正东方向走了200m到达地,再沿北偏东30°方向走,恰能到达目的地(如图),那么,由此可知,两地相距 m.
【答案】200
3. (2011甘肃兰州,17,4分)某水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,则两个坡角的和为 。
【答案】75
4. (2011广东株洲,11,3分)如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
【答案】40
5. (2011浙江义乌,15,4分)右图是市民广场到解百地下通道的手扶电梯示意图.其
中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点C上升的高度h是 ▲ m.
【答案】5
6. (2011广东茂名,13,3分)如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC= 米.
【答案】100
7. (2011湖北襄阳,14,3分)在207国道襄阳段改造工程中,需沿AC方向开山修路(如图3所示),为了加快施工速度,需要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=1000m,∠D=50°.为了使开挖点E在直线AC上,那么DE= m.(供选用的三角函数值:sin50°=0.7660,cos50°=0.6428,tan50°=1.192)
【答案】642.8
8. (2011内蒙古乌兰察布,16,4分)某厂家新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为和,大灯A与地面离地面的距离为1m则该车大灯照亮地面的宽度BC是 m .(不考虑其它因素)
【答案】1.4
9. (2011重庆市潼南,16,4分)如图,某小岛受到了污染,污染范围可
以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形
区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD= 30°,∠ACD= 60°,则直径AD= 米.(结果精确到1米)
(参考数据: )
【答案】260
三、解答题
1. (2011浙江金华,19,6分)生活经验表明,靠墙摆放的梯子,当50°≤α≤70°(α为梯子与地面所成的角),能够使人安全攀爬,现在有一长为6米的梯子AB,试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
【解】由题意知,当α越大,梯子的顶端达到的最大高度越大.因为当50°≤α≤70°时,能够使人安全攀爬,所以当α=70°时AC最大.
在Rt△ABC中,AB=6米,α=70°,
sin70°=,即0.94≈,解得AC ≈5.6.
答:梯子的顶端能达到的最大高度AC≈5.6米.
2. (2011安徽,19,10分)如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长.
(参考数据:=1.73)
【答案】∵OA, OB=OC=1500,
∴AB=(m).
答:隧道AB的长约为635m.
3. (2011广东东莞,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即
解得
小明家到公路的距离AD的长度约为68.2m. ……………………………………………8分
4. (2011江苏扬州,25,10分)如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.
(1)求垂直支架CD的长度。(结果保留根号)
(2)求水箱半径OD的长度。(结果保留三个有效数字,参考数据:,)
【答案】解:(1)在Rt△DCE中,∠CED=60°,DE=76,
∵sin∠CED= ∴DC=DE×sin∠CED = 38 (厘米)
答:垂直支架CD的长度为38厘米。
(2)设水箱半径OD=x厘米,则OC=(38+x)厘米,AO=(150+x)厘米,
∵Rt△OAC中,∠BAC=30°
∴AO=2×OC 即:150+x=2(38+x)
解得:x=150-76≈18.52≈18.5(厘米)
答:水箱半径OD的长度为18.5厘米。
5. (2011山东德州20,10分)某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为.测得A,B之间的距离为4米,,,试求建筑物CD的高度.
【答案】解:设建筑物CD与EF的延长线交于点G,DG=x米. …………1分
在△中,,即. …………2分
在△中,,即. …………3分
∴,.
∴ . ………5分
∴. ………6分
解方程得:=19.2. ………8分
∴ .
答:建筑物高为20.4米. ………10分
6. (2011山东威海,23,10分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠E=45°,∠A=60°,AC=10,试求CD的长.
【答案】 解:过点B作BM⊥FD于点M.
在△ACB中,∠ACB=90°, ∠A=60°,AC=10,
∴∠ABC=30°, BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=30°.
∴
在△EFD中,∠F=90°, ∠E=45°,
∴∠EDF=45°,
∴.
∴.
7. (2011山东烟台,21,8分)综合实践课上,小明所在小组要测量护城河的宽度。如图所示是护城河的一段,两岸ABCD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)
【答案】解:过点F作FG∥EM交CD于G.
则MG=EF=20米.
∠FGN=∠α=36°.
∴∠GFN=∠β-∠FGN=72°-36°=36°.
∴∠FGN=∠GFN,
∴FN=GN=50-20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin72°=30×0.95≈29(米).
8. (2011浙江绍兴,20,8分)为倡导“地摊生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图,车架档与的长分别为45cm,60cm,且它们相互垂直,座杆的长为20cm,点在同一条直线上,且,如图2.
(1)求车架档的长
(2)求车座点到车架档的距离.
(记过精确到1cm,参考数据:)
【答案】解(1)
=75 cm
车档架的长为75 cm
(2)过点作,垂足为点,
距离
车座点到车档架的距离是63cm
9. (2011浙江省,21,10分)图1为已建设封顶的16层楼房和其塔吊图,图2为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地面.
(1)求16层楼房DE的高度;
(2)若EF=16m,求塔吊的高CH 的长(精确到0.1m).
【答案】据题意得:DE=3.5×16=56,AB=EF=16
∵∠ACB=∠CBG-∠CAB=15°,
∴∠ACB =∠CAB
∴CB=AB=16. ∴CG=BC×sin30°= 8
CH=CG+HG=CG+DE+AD=8+56+5=69.
∴塔吊的高CH的长为69m.
10.(2011浙江台州,21,10分)丁丁要制作一个形如图1的风筝,想在一个矩形材料中裁剪出如图2 阴影所示的梯形翅膀,请你根据图2中的数据帮助丁丁计算出BE,CD的长度(精确到个位,)[来源:21世纪教育网]
【答案】解:在Rt△BEC中,∠BCE=30 ,EC=51,∴BE=≈30,AE=64
在Rt△AFD中,∠FAD=45 ,FD=FA=51,∴CD=64—51≈13
∴CD=13cm,BE=30cm.
11. (2011浙江丽水,19,6分)生活经验表明,靠墙摆放的梯子,当50°≤α≤70°(α为梯子与地面所成的角),能够使人安全攀爬,现在有一长为6米的梯子AB,试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
【解】当α=70°时,梯子顶端达到的最大高度,
∵sinα=,
∴AC = sin70°×6≈0.94×6=5.64≈5.6(米)
答:人安全攀爬梯子时,梯子的顶端达到的最大高度约5.6米.
12. (2011江西,22,9分)图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形。当点O到BC(或DE)的距离大于或等于⊙O的半径时(⊙O是桶口所在圆,半径为OA),提手才能从图甲的位置转到图乙的位置,这样的提手才合格,现在用金属材料做了一个水桶提手(如图丙A-B-C-D-E-F,C-D是弧CD,其余是线段),O是AF的中点,桶口直径AF=34cm,AB=FE=5cm,∠ABC=∠FED=149°。请通过计算判断这个水桶提手是否合格。
(参考数据:≈17.72,tan73.6°≈3.40,sin75.4°≈0.97。)
【答案】解:连结OB,过点O作OG⊥BC于点G.在Rt△ABO中,
AB=5,AO=17,∴tan∠ABO=,
∴∠ABO=73.6°,
∴∠GBO=∠ABC-∠ABO=149°-73.6°=75.4°
又∵OB=≈17.72,
∴在Rt△OBG中,OG=OB×sin∠GBO=17.72×0.97≈17.19>17.
∴水桶提手合格.
13. (2011湖南常德,24,8分)青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图7所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)
【答案】解:在Rt△BCD中,
∵∠BCD=90°-30°=60°
∴,则
在Rt△ABD中,[来源:21世纪教育网]
∵∠ABD=60°
∴
即
∴
故约7秒钟后灰太狼能抓到懒羊羊.
14. (2011湖南邵阳,20,8分)崀山成功列入世界自然遗产名录后,景区管理部门决定在八角寨假设旅游索道设计人员为了计算索道AB(索道起点为山脚B处,终点为山顶A处)的长度,采取了如图(八)所示的测量方法。在B处测得山顶A的仰角为16°,查阅相关资料得山高AC=325米,求索道AB的长度。(结果精确到1米,参考数据sin16°≈0.28,cos16°≈0.96,tan16°≈0.29)
【答案】解:AB=AC÷sin 16°= 325÷0.28≈1161米。
15. (2011湖南益阳,18,8分)如图8,AE是位于公路边的电线杆,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根水泥撑杆BD,用于撑起拉线.已知公路的宽AB为8米,电线杆AE的高为12米,水泥撑杆BD高
为6米,拉线CD与水平线AC的夹角为67.4°.求拉线CDE
的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大
小忽略不计).
(参考数据:,,)
【答案】解:⑴在Rt中,,
(m).
,
,,,
(m).
(m)
16. (2011江苏连云港,24,10分)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水答道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5 方向,前行1200m,到达点Q处,测得A位于北偏西49 方向,B位于南偏西41 方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.
(参考数据:cos41 ≈0.75)
【答案】(1)∵B位于P点南偏东24.5 方向,∴∠BPQ=65.5 ,又∵B位于Q点南偏西41 方向, ∴∠PQB=49 , ∴∠PBQ=65.5 , ∴PQ=BQ(等角对等边),(2)∵点P处测得A在正北方向,在Rt△APQ中,,∴AQ=1600,由(1)得PQ=BQ=1200,∵在点Q处,测得A位于北偏西49 方向,B位于南偏西41 方向,∴∠AQB=90 ,在Rt△ABQ中,AB=(m).
17.
18. (2011江苏苏州,25,8分)如图,小明在大楼30米高(即PH=30米)得窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于________度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据:≈1.732).
【答案】解:(1)30.
(2)由题意得:∠PBH=60°,∠APB=45°.
∵∠ABC=30°,∴∠APB=90°.
在Rt△PHB中,PB==20,
在Rt△PBA中,AB=PB=20≈34.6.
答:A、B两点间的距离约34.6米.
19. (2011江苏宿迁,23,10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取=1.732,结果精确到1m)
【答案】
解:设CE=xm,则由题意可知BE=xm,AE=(x+100)m.
在Rt△AEC中,tan∠CAE=,即tan30°=[来源:21世纪教育网]
∴,3x=(x+100)
解得x=50+50=136.6
∴CD=CE+ED=(136.6+1.5)=138.1≈138(m)
答:该建筑物的高度约为138m.
20.(2011江苏泰州,23,10分)一幢房屋的侧面外壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°.外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG ∥EH,GH=2.6cm , ∠FGB=65°.
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
【答案】解:(1)设CD与FG交于点M,由CD∥AB,∠FGB=65°,可得∠FGC=65°,又∠OCD=25°,于是在△FGC中,可得∠CFM=90°,即GF⊥OC.
(2)过点G作GN⊥HE,则GN=EF,在Rt△GHN中,
sin ∠EHG=,即GN=GH sin ∠EHG=2.6 sin 65°=2.6×0.91=2.366≈2.4cm.
21. (2011广东汕头,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即
解得
小明家到公路的距离AD的长度约为68.2m.
22. (2011山东聊城,21,8分)被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑,铁塔由塔身和塔座两部分组成(如图①).为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G(如图②),求铁塔EF的高(结果精确到0.1米).
【答案】设EG=x米,在Rt△CEG中,∵∠ECG=45°,∴∠CEG=45°,∴∠ECG=∠CEG,∴CG=EG,=x米,在Rt△DEG中,∠EDG=60°,tan∠EDB=,∴DG=,∵CG-DG=CD=6, ∴=6,解得x=9+,∴EF=EG+FG=9++16≈158,所以铁塔高约为158米
23. (2011山东潍坊,19,9分)今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔121米,C点海拔721米.
(1)求B点的海拔;
(2)求斜坡AB的坡度.
【解】(1)如图所示,过点C作CF⊥AM,F为垂足,过点B作BE⊥AM,BD⊥CF,E、D为垂足.
∵在C点测得B点的俯角为30°,
∴∠CBD=30°,又∵BC=400米,
∴CD=400×sin30°=400×=200(米).
∴B点的海拔为721-200=521(米).
(2)∵BE=521-121=400(米),AB=1040米,
∴(米).
∴AB的坡度,所以斜坡AB的坡度为1:2.4.
24. (2011广东汕头,19,7分)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D.点C落在点E处,BF是折痕,且BF= CF =8.
(l)求∠BDF的度数;
(2)求AB的长.
【解】(1)∵BF=CF,∠C=,
∴∠FBC=,∠BFC=
又由折叠可知∠DBF=
∴∠BDF=
(2)在Rt△BDF中,
∵∠DBF=,BF=8
∴BD=
∵AD∥BC,∠A=
∴∠ABC=
又∵∠FBC=∠DBF=
∴∠ABD=
在Rt△BDA中,
∵∠AVD=,BD=
∴AB=6.
25. (2011四川广安,26,9分)某校初三课外活动小组,在测量树高的一次活动中,如图7所示,测得树底部中心A到斜坡底C的水平距离为8. 8m.在阳光下某一时刻测得1米的标杆影长为0.8m,树影落在斜坡上的部分CD= 3.2m.已知斜坡CD的坡比i=1:,求树高AB。(结果保留整数,参考数据:1.7)
【答案】解:如图,延长BD与AC的延长线交于点E,过点D作DHAE于H
∵CD=3.2 ∴DH=1.6 CH=
∵ ∴HE=1.28
∵ ∴AB=16
26. (2011四川内江,20,9分)放风筝是大家喜爱的一种运动。星期天的上午小明在大洲广场上放风筝。如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°。为了便于观察,小明迅速向前边移动边收线到达了离A处7米的B处,此时风筝线BD与水平线的夹角为45°。已知点A、B、C在同一条直线上,∠ACD=90°。请你求出小明此时所收回的风筝线的长度是多少米?(本题中风筝线均视为线段,,,最后结果精确到1米)
【答案】设BC=CD=x米,得
,解得
∴AD-BD=2x-=(米)
27. (2011四川宜宾,22,7分)如图,飞机沿水平方向(A,B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个求距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
【答案】解:此题为开放题,答案不惟一,只要方案设计合理,可参照给分
⑴如图,测出飞机在A处对山顶的俯角为,测出飞机在B处对山顶的俯角为,测出AB的距离为d,连接AM,BM.
⑵第一步,在中, ∴
第二步,在中, ∴
其中,解得.
28. (2011重庆綦江,20,6分)如图,小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD, 点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21米,请你帮小刚求出该屏幕上端与下端之间的距离CD. (结果保留根号)
【答案】:解:∵∠CBE=45° CE⊥AE
∴CE=BE=21
AE=21+6=27
在Rt△ADE中,∠DAE=30°
∴DE=AE×tan30°=27×=9
∴CD=CE-DE=21-9
∴该屏幕上端与下端之间的距离CD=21-9 (米).
29. (2011江西南昌,22,9分)图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形。当点O到BC(或DE)的距离大于或等于⊙O的半径时(⊙O是桶口所在圆,半径为OA),提手才能从图甲的位置转到图乙的位置,这样的提手才合格,现在用金属材料做了一个水桶提手(如图丙A-B-C-D-E-F,C-D是弧CD,其余是线段),O是AF的中点,桶口直径AF=34cm,AB=FE=5cm,∠ABC=∠FED=149°。请通过计算判断这个水桶提手是否合格。
(参考数据:≈17.72,tan73.6°≈3.40,sin75.4°≈0.97。)
图甲 图乙 图丙
【答案】解:连结OB,过点O作OG⊥BC于点G.在Rt△ABO中,
AB=5,AO=17,∴tan∠ABO=,
∴∠ABO=73.6°,
∴∠GBO=∠ABC-∠ABO=149°-73.6°=75.4°
又∵OB=≈17.72,
∴在Rt△OBG中,OG=OB×sin∠GBO=17.72×0.97≈17.19>17.
∴水桶提手合格.
30. (2011安徽芜湖,18,8分)如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点的仰角为,再沿着的方向后退20m至处,测得古塔顶端点的仰角为.求该古塔BD的高度(,结果保留一位小数).
【答案】
解:根据题意可知:
在中,由得. …………………………2分
在中,由.得………………………4分
又∵,∴.∴(m).………………7分
答:该古塔的高度约为27.3m.
31. (2011山东济宁,18, 5分)日本福岛出现核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场检测与海水采样,针对核泄漏在极端情况下对海洋的影响及时开展分析评估.如图上午9时,海检船位于A处,观测到某港口城市P位于海检船的北偏西67.5°,海检船以21海里/时的速度向正北方向行驶,下午2时海检船到达B处,这时观测到城市P位于海检船的南偏西36.9°方向,求此时海检船所在B处与城市P的距离?(参考数据:sin36.9°≈,tan36.9°≈,sin67.5°≈,tan67.5°≈)
【答案】解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=,∴AC=.…………2分
在Rt△PCB中,∵tan∠B=,∴BC=.…………4分
∵AC+BC=AB=21×5,∴,解得.
∵,∴(海里).
∴海检船所在B处与城市P的距离为100海里.………………6分
32. (2011四川成都,16,6分)如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)
【答案】解:由题意可知,在Rt△ABC中,AB=500,∠ACB=90°-60°=30°,
∵∠ACB=,
∴BC=(),
∴该军舰行驶的路程为米.
33. (2011广东省,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即
解得
小明家到公路的距离AD的长度约为68.2m.
34. (2011广东省,19,7分)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D.点C落在点E处,BF是折痕,且BF= CF =8.
(l)求∠BDF的度数;
(2)求AB的长.
【解】(1)∵BF=CF,∠C=,
∴∠FBC=,∠BFC=
又由折叠可知∠DBF=
∴∠BDF=
(2)在Rt△BDF中,
∵∠DBF=,BF=8
∴BD=
∵AD∥BC,∠A=
∴∠ABC=
又∵∠FBC=∠DBF=
∴∠ABD=
在Rt△BDA中,
∵∠AVD=,BD=
∴AB=6.
35. (2011江苏淮安,23,10分)题23-1图为平地上一幢建筑物与铁塔图,题23-2图为其示意图.建筑物AB与铁塔CD都垂直于底面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°.求铁塔CD的高度.
题23-1图 题23-2图
【答案】解:如图,设过点A的水平线与CD交于点E,由题意得
∠AEC=∠AED=90°,∠CAE=60°,∠DAE=45°,AE=BD=30m,
∴CD=CE+DE=AE·tan60°+AE·tan45°=30+30(m).
答:铁塔CD的高度为(30+30)m.
36. .(2011江苏南京,25,7分)如图,某数学课外活动小组测量电视塔AB的高度,他们借助一个高度为30m的建筑物CD进行测量,在点C处塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【答案】解:在中,=.
∴EC=≈().
在中,∠BCA=45°,∴
在中,=.∴.∴().
答:电视塔高度约为120.
37. (2011四川凉山州,23,8分)在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图,∥,坝高10m,迎水坡面的坡度,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面的坡度进行修改,修改后的迎水坡面的坡度。
求原方案中此大坝迎水坡的长(结果保留根号)
如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿方向拓宽2.7m,求坝顶将会沿方向加宽多少米?
【答案】
解:⑴过点作于。
在中,∵,且。
∴,
⑵过点作于。
在中,∵,且。
∴,
如图,延长至点,至点,
连接,
∵方案修改前后,修建大坝所需土石方
总体积不变。
。即 。
。
答:坝底将会沿方向加宽。
38. (2011江苏无锡,24,9分)(本题满分9分)如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D。飞机在A处时,测得山头C、D在飞机前方,俯角分别为60°和30°。飞机飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方。求山头C、D之间的距离。
【答案】
解:在Rt△ABD中,∵∠BAD = 30°,∴BD = AB·tan30° = 6 × = 2.………………(2分)
∵∠BAC = 60°,∠ABC = 30°,∴∠ACB = 90°,∴BC = AB·cos30° = 6 × = 3.
…………(4分)
过点C作CE⊥BD于点E,则∠CBE = 60°,CE = BC·sin60° = .…………(6分)
∴BE = BC·cos60° = ,………………………………(7分)
DE = BD BE = 2 = .
∴在Rt△CDE中,CD = = = (km).
答:山头C、D之间的距离为(km).…………………………………………………(9分)
39. (2011湖北黄冈,21,8分)如图,防洪大堤的横断面是梯形,背水坡AB的坡比(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留三个有效数字,1.732).
【答案】 ≈36.0
40. (2011湖北黄石,22,8分)东方山是鄂东南地区的佛教胜地,月亮山是黄荆山脉第二高峰,山顶上有黄石电视塔,据黄石地理资料记载:东方山海拔453.20米,月亮山海拔442.00米。一飞机从东方山到月亮山方向水平飞行,在东方山山顶D的正上方A处测得月亮山山顶C的俯角为α,在月亮山山顶C的正上方B处测得东方山山顶D处的俯角为β,如图(7),已知tanα=0.15987,tanβ=0.15847,若飞机的飞行速度为180米/秒,则该飞机从A到B处需多少时间?(精确到0.1秒)
【答案】解:设AB=x米,根据题意得,
AD=x·tanβ=0.15847x
BC=x·tanα=0.15987x
0.15847x+453.20=0.15987x+442.00
解之得,0.0014x=11.2
x=8000
t=
t=44.4
答:该飞机从A到B处需44.4秒
41. (2011贵州贵阳,20,10分)
某过街天桥的设计图是梯形ABCD(如图所示),桥面DC与地面AB平行,DC=62米,AB=88米.左斜面AD与地面AB的夹角为23°,右斜面BC与地面AB的夹角为30°,立柱DE⊥AB于E,立柱CF⊥AB于F,求桥面DC与地面AB之间的距离.(精确到0.1米)
(第20题图)
【答案】解:在Rt△ADE中,∠A=23°,
∴AE=.
在Rt△BCF中,∠B=30°,
∴BF=.
∵DE⊥AB,CF⊥AB,AB∥CD,
∴CD=EF,DE=CF,
∴++62=88.
解得,DE≈6.4.
即桥面DC与地面AB之间的距离约为6.4米.
42. (2011江苏盐城,24,10分)如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:≈1.732)
【答案】过点B作BF⊥CD于F,作BG⊥AD于G.
在Rt△BCF中,∠CBF=30°,∴CF=BC·sin30°= 30× =15.
在Rt△ABG中,∠BAG=60°,∴BG=AB·sin60°= 40× eq \f(,2) = 20.
∴CE=CF+FD+DE=15+20+2=17+20≈51.64≈51.6(cm)cm.
答:此时灯罩顶端C到桌面的高度CE约是51.6cm. [来源:21世纪教育网]
43. (2011广东中山,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即[来源:21世纪教育网]
解得
小明家到公路的距离AD的长度约为68.3m.
44. (2011湖北鄂州,21,8分)如图,防洪大堤的横断面是梯形,背水坡AB的坡比(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留三个有效数字,1.732).
【答案】 ≈36.0
45. (2011广东湛江24,10分)五一期间,小红到美丽的世界地质公园光岩参加社会实践活动,在景点P处测得景点B位于南偏东方向,然后沿北偏东方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.(结果精确到0.1米)
【答案】过P作,垂足为D,则,[来源:21世纪教育网21世纪教育网]
所以,且米,
所以AD=50米,
又,,所以DB=DP,而,
所以米。
46. (2011贵州安顺,21,8分)一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈)
【答案】过点C作CDAB于D ,
由题意,,设CD = BD = x米,则AD =AB+BD =(40+x)米,
在Rt中,tan=,则,解得x = 60(米).
47. (2011湖南湘潭市,19,6分)(本题满分6分)
莲城中学九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆
顶端A的仰角为30°,向前走了6米到达D点,在D点测得旗杆顶端A的仰角
为60°(测角器的高度不计).
⑴ AD=_______米;
⑵ 求旗杆AB的高度().
【答案】解:(1)6
(2)在Rt△ABD中,(米)所以旗杆AB的高度为5.19米.
48. (2011湖北荆州,21,8分)(本题满分8分)某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝,其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切,上、下桥斜面的坡度i=1:3.7,桥下水深OP=5米,水面宽度CD=24米.设半圆的圆心为O,直径AB在直角顶点M、N的连线上,求从M点上坡、过桥、下坡到N点的最短路径长.(参考数据:,,)
【答案】 解:连结OD、OE、OF,由垂径定理知:PD= 1 2 CD=12(m)
在Rt△OPD中,(m),
∴OE=OD=13m
∵tan∠EMO=i= 1: 3.7 , ≈ 1:3.7
∴∠EMO=15°
由切线性质知∠OEM=90°
∴∠EOM=75°
同理得∠NOF=75°
∴∠EOF=180°-75°×2=30°
在Rt△OEM中,tan15°=
∴EM=3.7×13=48.1(m)
又EF的弧长=30π×13÷180 =6.5(m)
∴48.1×2+6.5=102.7(m)
即从M点上坡、过桥、再下坡到N点的最短路径长为102.7米.
49.
50.
2011中考模拟分类汇编:直角三角形与勾股定理
选择题
1、(2011浙江杭州模拟14)如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处. 已知AB=, ∠B=30°, 则DE的长是( ).
A. 6 B. 4 C. D. 2
答案:B
2.(2011湖北崇阳县城关中学模拟)直角三角形两直角边和为7,面积为6,则斜边长为( )
A. 5 B. C. 7 D.
答案:A
3.(2011年杭州市上城区一模)梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是S1、S2、S3 ,
且S1 +S3 =4S2,则CD=( )
A. 2.5AB B. 3AB C. 3.5AB D. 4AB
答案:B
4.(2011年浙江省杭州市模2)直角三角形两直角边和为7,面积为6,则斜边长为( )
A. 5 B. C. 7 D.
答案:A
填空题
1、(2011年北京四中三模)如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5cm,则正方形A、B、C、D的面积和是 .
答案:25cm2
2.(2010-2011学年度河北省三河市九年级数学第一次教学质量检测试题)如图是两个全等的三角形纸片,其三边长之比为3:4:5,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为SA,SB,已知SA+SB=13,则纸片的面积是 .
答案:36
3、(2011浙江杭州模拟15)如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连结CD.若AB=4cm. 则△BCD的面积为 .
答案:
4.(2011年宁夏银川)将一副三角尺如图所示叠放在一起,若=14cm,则阴影部分的面积_________cm2.
答案:
5.(2011浙江省杭州市8模)如图1,是我国古代著名的“赵爽弦图”的示意图,它是由四全等的直角三角形围成的,若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是__________;
(第5题图)
答案:76
6、(2011年浙江杭州二模)如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米, 那么该古城墙的高度是 米.
答案:8
7、(2011年浙江杭州八模)如图,小明在A时测得某树的影长为3米,B时又测得该树的影长为12米,若两次日照的光线互相垂直,则树的高度为_____米.
答案:6
第8题图
8、(2011年浙江杭州八模)如图1,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是__________;
答案:76
9. (浙江省杭州市党山镇中2011年中考数学模拟试卷)如图,将边长为的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交于点M、N,DFAB,垂足为D,AD=1,则重叠部分的面积为 .
答案:
B组
1.( 2011年杭州三月月考)将一副三角板按如图1位置摆放,使得两块三角板的直角边AC和MD重合.已知AB=AC=8 cm,将△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积是 ▲ cm2
答案:
2.(2011年重庆江津区七校联考一模)一元二次方程的两根恰好是一直角三角形的两边长,则该直角三角形的面积为 。
答案: 6或
3、(2011年浠水模拟2)如图1,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=5,将四个 直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是_______________;
答案: 76
4. (2011年杭州市模拟)侧棱长为cm的直三棱柱的三个侧面面积分别为、和,则该棱柱上底面的面积为 .
答案:
5. (2011年海宁市盐官片一模)已知是直角三角形的三条边,且,斜边上的高为,则下列说法中正确的是 。(只填序号)
①;②;
③由可以构成三角形;④直角三角形的面积的最大值是.
答案:②③
6.(2011北京四中一模)在数学活动课上名师带领学生去测量河两岸A, B两处之间的距离,先从A处出发与AB成90°方向,向前走了10米到C处,在C处测得∠ACB=60°(如图所示),那么A,B之间的距离约为 米(计算结果精确到0.1米)
答案:17
7. (2011深圳市中考模拟五)等腰三角形的腰长为2,腰上的高为1,则它的底角等于 .
答案: 15°或75°
解答题
1、(2011浙江杭州模拟14)
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当时,求线段的长;
(2)点M在线段AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形,若可以,请直接写出t的值(不需解题步骤);若不可以,请说明理由.
(3)若△PCQ的面积为y,请求y关于出t 的函数关系式及自变量的取值范围;
答案:
解:(1)由Rt△AQM∽Rt△CAD. ……………………………………………2分
∴. 即,∴. …………………………………1分
(2)或或4. ……………………………………………3分
(3)当0<t<2时,点P在线段CD上,设直线l交CD于点E
由(1)可得. 即QM=2t.∴QE=4-2t.………………………2分
∴S△PQC =PC·QE= ………………………………………………1分
即
当>2时,过点C作CF⊥AB交AB于点F,交PQ于点H.
.
由题意得,.
∴ . ∴.
∴ . ∴.
∴ 四边形AMQP为矩形.
∴ PQ∥.CH⊥PQ,HF=AP=6- t
∴ CH=AD=HF= t-2 …………………………………………………………1分
∴S△PQC =PQ·CH= ………………………………………1分
即y=
综上所述 或y= ( 2<<6) …………………1分
2、(2011浙江杭州模拟16)
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即 “以数解形”;或者借助形的几何直观性来阐明数之间的某种关系,即 “以形助数”。
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解: 设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)
答案:
解:(1)显然,方程x2-14x+48=0的两根为6和8, 1分
又AC>BC
∴AC=8,BC=6
由勾股定理AB=10
△ACD∽△ABC,得AC2= AD·AB
∴AD=6.4 -------------------------------2分
∵CM平分∠ACB
∴AM:MB=AC:CB
解得,AM=--------------------------------- 1分
∴MD=AD-AM=-----------------------------1分
(2)解:不访设AB=a,CD=d,AC=b,BC=c
由三角形面积公式,得AB·CD=AC·BC
2AB·CD=2AC·BC -------------------------1分
又勾股定理,得AB2=AC2+BC2
∴AB2+2AB·CD =AC2+BC2+2AC·BC(等式性质)
∴AB2+2AB·CD =(AC+BC)2----------------------1分
∴AB2+2AB·CD+CD2 >(AC+BC)2--------------------2分
∴(AB+CD) 2 >(AC+BC)2
又AB、CD、AC、BC均大于零
∴AB+CD>AC+BC即a+d>b+c--------------------1分
3. (2011年北京四中中考全真模拟17)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米?
1、探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和
(或差)的有关问题,这种方法称为面积法。请你运用面积法求解下列问题:在等腰三
角形ABC中,AB=AC,BD为腰AC上的高。
(1)若BD=h,M时直线BC上的任意一点,M到AB、AC的距离分别为。
若M在线段BC上,请你结合图形①证明:= h; 图①
当点M在BC的延长线上时,,h之间的关系为 .
(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线:y = x + 6 ; :y = -3x+6
若上的一点M到的距离是3,请你利用以上结论求解点M的坐标。
(1)证明:连结AM
①∵, EM⊥AB , MF⊥AC, BD⊥AC
∴AC.h = AB. + AC.
又∵AB = AC
∴h = + ………………………………………………2分
② - = h ………………………………………………3分
(2)由题意可知,DE = DF =10,
∴△EDF是等腰三角形。………………………………………4分
当点M在线段EF上时,依据(1)中结论,
∵h = EO=6,∴M到DF(即x轴)的距离也为3.
∴点M的纵坐标为3,此时可求得M(1,3)……………………6分
当点M在射线FE上时,依据(1)中结论
∵h = EO=6,∴M到DF(即x轴)的距离也为9.
∴点M的纵坐标为9,此时可求得M(-1,9)………………………………8分
故点M的坐标为(1,3)或(-1,9)
4、(2011年江苏盐都中考模拟)
解:原式=(4分)
5.(2011年黄冈中考调研六)(满分14分) 如图,以等边△OAB的边OB所在直线为x轴,点O为坐标原点,使点A在第一象限建立平面直角坐标系,其中△OAB边长为6个单位,点P从O点出发沿折线OAB向B点以3单位/秒的速度向B点运动,点Q从O点出发以2单位/秒的速度沿折线OBA向A点运动,两点同时出发,运动时间为t(单位:秒),当两点相遇时运动停止。
点A坐标为_____________,P、Q两点相遇时交点的坐标为________________;
当t=2时,____________;当t=3时,____________;
设△OPQ的面积为S,试求S关于t的函数关系式;
当△OPQ的面积最大时,试求在y轴上能否找一点M,使得以M、P、Q为顶点的三角形是Rt△,若能找到请求出M点的坐标,若不能找到请简单说明理由。
答案.
A点坐标为、交点坐标为(
当t=2时,; 当t=3时,
对(3)中的分段函数进行计算后得知当t=2,S有最大值,此时P与A重合,OP=6,OQ=4,过P作PC⊥OB于C点,计算得OC=3,AC=,CQ=1,PQ=
如图①,过P作PM⊥PQ交y轴于M点,过M作MN⊥AC于N,则MN=OC=3,易得Rt△PMN∽△QPC,有即,得PN=,MO=NC=故M点坐标为
过Q作MQ⊥PQ交y轴于M点,通过△MOQ∽△QCP,求得M坐标为
以PQ为直径作⊙D,则⊙D半径r为,再过P作PE⊥y轴于E点,过D作DF⊥y轴于F点,由梯形中位线求得DF=,显然r<DF,故⊙D与y同无交点,那么此时在y轴上无M点使得△MPQ为直角三角形.
综上所述,满足要求的M点或
6. (2011浙江省杭州市8模)(本题满分8分)某商场为了迎接“六一”儿童节的到来,制造了一个超大的“不倒翁”。小灵对“不倒翁”很感兴趣,原来“不倒翁”的底部是由一个空心的半球做成的,并在底部的中心(即图中的C处)固定一个重物,再从正中心立起一根杆子,在杆子上作些装饰,在重力和杠杆的作用下,“不倒翁”就会左摇右晃,又不会完全倒下去。小灵画出剖面图,进行细致研究:圆弧的圆心为点O,过点O的木杆CD长为260㎝,OA、OB为圆弧的半径长为90㎝(作为木杆的支架),且OA、OB关于CD对称,弧AB的长为30㎝。当木杆CD向右摆动使点B落在地面上(即圆弧与直线l相切于点B)时,木杆的顶端点D到直线l的距离DF是多少㎝?
(第6题)
解:由弧AB的长可得,∠AOB=60°,
从而∠BOE=∠COB=30°,(2分)
∵OB=90cm,
∴OE=cm,(2分)
∴DE=170+ cm, (2分)[来源:21世纪教育网21世纪教育网]
∴DF=180+ cm (2分)
7.(2011广东南塘二模)如图,在小山的东侧A处有一热气球,以每分钟30m
的速度沿着仰角为60°的方向上升,20分钟后升到B处,这时
气球上的人发现在A的正西方向俯角为45°的C处有一着火点,
求气球的升空点A与着火点C的距离(结果保留根号).
答案:过B作BD⊥CA于D,则AB=600m,AD=300m,BD=CD=300m,CA=300(-1)m。
8.(2011深圳市全真中考模拟一)△ABC中,BC=,AC=,AB=c.若,如图l,根据勾股定理,则。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想与的关系,并证明你的结论.
答案:解:若△ABC是锐角三角形,则有 …… (1分)
若△ABC是钝角三角形,为钝角,则有。 (2分)
当△ABC是锐角三角形时,
证明:过点A作ADBC,垂足为D,设CD为,则有BD=……(3分)
根据勾股定理,得
即。
∴…………………………(5分)
∵,
∴。
∴。…………………………(6分)
当△ABC是钝角三角形时,
证明:过B作BDAC,交AC的延长线于D。
设CD为,则有…………………………(7分)
根据勾股定理,得.
即。…………………………(9分)
∵,
∴,
∴。…………………………(10分)
解直角三角形
一、选择题
1.(2010年教育联合体)在△ABC中,已知AB=5,AC=3,BC=4,则下列结论中正确的是( )
A.sinA= B.cosB= C.tanA= D.tanB=
答案:A
2.(2010年安徽省模拟)如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE的长是( )
A. B.
C. D.
答案:D
3.(2010年北京市朝阳区模拟)正方形网格中,如图放置,则的值为( )
A. B.2 C. D.
答案:D
4.(2010年三亚市月考)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,下列各式成立的是( )
A. b=a·sinB B. a=b·cosB C. a=b·tanB D. b=a·tanB
答案D
5.(2010年聊城冠县实验中学二模)正方形网格中,∠AOB如下图放置,则
tan∠AOB的值为( )
A.2 B. C. D.
答案A
6.(2010年聊城冠县实验中学二模)如下图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①BD=BE,②∠A=∠BHE,③AB=BH,④△BHD∽△BDG。其中正确的结论是( )
A.①②③④ B.①②③ C.①②④ D.②③④
答案B
7.(2010年江西南昌一模)如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
A.(-,-)
B.(,)
C.(-,-)
D.(0,0)
答案:A
8.(2010年武汉市中考拟)如图,AB为⊙O的直径,CA切⊙O于A,
CB交⊙O于D,若CD=2,BD=6,则sinB=( )
A. B. C. D.
答案:A
9.(2010年厦门湖里模拟)在Rt△ABC中,∠C=90°,AB=13,BC=5,则 ( )
A. B. C. D.
答案:B
10.(2010年杭州月考)已知在中,,则的值为( )
A. B. C. D.
答案:A
11.(2010年天水模拟)如图为了测量某建筑物AB的高度,在平地上C 处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D 处,在D处测得建筑物项端A的仰角为45°,则建筑物AB的高度等于( )
A.6()m B.6()m
C.12()m D.12()m
答案:A
12.(2010年广州中考数学模拟试题一)已知α为等边三角形的一个内角,则cosα等于( )
A. B. C. D.
答:A
13.( 2010年山东菏泽全真模拟1) 王英同学从A地沿北偏西60 方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地 ( )
A.m B.100 m C.150m D.m
答案:D
14.(2010年江苏省泰州市济川实验初中中考模拟题)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC的值为( )
A. eq \f(3,10) B. eq \f(2,5) C. eq \f(,2) D.
二、填空题
1.(2010年安徽省模拟)化简 .
答案:
2.(2010年三亚市月考).如图,铁路的路基的横断面为等腰梯形,其腰的坡度为1:1.5,上底宽为6m,路基高为4m,则路基的下底宽为 .
答案: 18m ;
3.(2010年天水模拟)如图,某公园入口处原有三阶台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡的坡度i=,则AC的长度是 .
答案:240cm
4.(2010年重庆市綦江中学模拟1)如图,身高1.6m的小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为6m,那么这棵树高大约为(结果精确到0.1m,其中小丽眼睛距离地面高度近似为身高) .
答案: 5.1m
5.(2010年江西南昌一模)如图,在正方形网格中,∠AOB的正切值是
答案:
6.(2010年山东新泰)若△ABC中,∠C=90°,AC:BC=3:4,那么sinA= .
答案:
7.(2010年天津市中考模拟)如图,有一个边长为5的正方形纸片,要将其剪拼成边长分别为的两个小正方形,使得.①的值可以是________(写出一组即可);②请你设计一种具有一般性的裁剪方法,在图中画出裁剪线,并拼接成两个小正方形,同时说明该裁剪方法具有一般性:
__________________________________________
_________________________________________
_________________________________________
答案:①3,4(提示:答案不惟一);
②裁剪线及拼接方法如图所示:图中的点可以是以为直径的半圆上的任意一点(点除外).的长分别为两个小正方形的边长
8.(2010年辽宁抚顺中考模拟)将一个含30°角的三角板和一个含45°角的三角板如图摆放,与完全重合,,,则 .
答案:
9.(2010年江西省统一考试样卷)比较大小:sin33°+cos33° 1.(可用计算器辅助)
答案:>.
10.(2010年河南中考模拟题1)
答案:
三、解答题
1.(2010年湖里区二次适应性考试))如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
(3)连结OA,AB,在x轴下方的抛物线上是否存在点N,使△OBN与△OAB相似?若存在,求出N点的坐标;若不存在,说明理由.
答案:(1)由题意,可设抛物线的解析式为,
∵抛物线过原点,
∴, .
∴抛物线的解析式为.
(2)和所求同底不等高,,
∴的高是高的3倍,即M点的纵坐标是.
∴,即.
解之,得 ,.
∴满足条件的点有两个:,.
(3)不存在.
由抛物线的对称性,知,.
如图,若与相似,必有.
设交抛物线的对称轴于点,显然.
∴直线的解析式为.
由,得,.
∴ .
过作轴,垂足为.在中,,,
∴.
又OB=4,
∴,,与不相似.
同理,在对称轴左边的抛物线上也不存在符合条件的点.
所以在该抛物线上不存在点N,使与相似.
2.(2010年北京市朝阳区模拟) .
解:原式=
=
3.(2010年北京市朝阳区模拟)小明站在A处放风筝,风筝飞到C处时的线长为20米,这时测得∠CBD=60°,若牵引底端B离地面1.5米,求此时风筝离地面高度。(计算结果精确到0.1米,)
解:在Rt△BCD中,CD=BC×sin60°=20×
又∵DE=AB=1.5
∴CE=CD+DE=(米)
答:此时风筝离地面的高度约是18.8米.
4.(2010年教育联合体)计算:
原式= =2
5.(2010年安徽省模拟)为测量大楼CD的高度,某人站在A处测得楼顶的仰角为450,前进20m后到达B处测得楼顶的仰角为600,求大楼 CD的高度。
解:如图,依题意得∠CBD=600 , ∠CDB=900,设BD=x m,则AD=(20+x) m
CD= m
在Rt△ACD中,∠CAD=450 , ∠CDA=900
∴AD=CD
∴20+x=
∴x=10(+1)
∴CD=x=(30+) m ,即楼高为(30+) m
6.(2010年三亚市月考) 如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,试求该塔的高度。(≈1.41,≈1.73)
解:由题意可知 CD=10米,BD=1.5米,∠ACD=60°.
在Rt△ACD中,AD=CDtan60°= 10
∴AB=AD+DB=10 + 1.5 ≈10×1.73 + 1.5 =18.8(米)
答:该塔的高度是18.8米
7.(2010年聊城冠县实验中学二模)九年级甲班数学兴趣小组组织社会实践活动,目的是测量一山坡的护坡石坝高度及石坝与地面的倾角.
(1)如上图1,小明所在的小组用一根木条EF斜靠在护坡石坝上,使得BF与BE的长度相等,如果测量得到∠EFB=36°,那么的度数是___________;
(2)如上图2,小亮所在的小组把一根长为5米的竹竿AG斜靠在石坝旁,量出竿长1米时离地面的高度为0.6米,请你求出护坡石坝的垂直高度AH;
(3)全班总结了各组的方法后,设计了如上图3方案:在护坡石坝顶部的影子处立一根长为米的杆子PD,杆子与地面垂直,测得杆子的影子长为米,点P到护坡石坝底部B的距离为米,如果利用(1)得到的结论,请你用表示出护坡石坝的垂直高度AH。(,,)
解.(1)72°
(2)3米
(3)
8.(2010年年广州市中考六模)、如图,某中学科学楼高15米,计划在科学楼正北方向的同一水平地上建一幢宿舍楼,第一层是高2.5米的自行车场,第二层起为宿舍。已知该地区一年之中“冬至”正午时分太阳高度最低,此时太阳光线AB的入射角∠ABD=55°,为使第二层起能照到阳光,两楼间距EF至少是多少米?(精确到0.1米)。
(参考数据:tan55°=1.4281,tan35°=0.7002)。
答案:
由矩形BCEF得到CE=BF,BC=EF [来源:21世纪教育网]
得到∠CAB=55o
得到BC=ACtan55o BC=17.9米 作答
9.(2010年广州市中考七模)、如图,某电信公司计划修建一条连接B、C两地的电缆。测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长(结果保留根号).
解:画BE、CF均垂直于AM,垂足分别为E、F;画BD⊥CF于D.
则四边形BEFD是矩形. 设BD=x,由题意得
AF=CF=200,EF=BD=x,AE=200- x
∵∠CBD=60°,
∴CD=tan60°·BD=x,BE=DF=200-x
∵= tan∠BAE= tan30°=,
即=,
解得x =,
∴BC=2x= (m)
10.(2010年广东省中考拟)如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合,已知BC=6.
(1)三角尺旋转了多少度?连结CD,试判断⊿BCD的形状;
(2)求AD的长;
(3)连结CE,试猜想线段AC与CE的大小关系,并证明你的结论.
解:(1)三角尺旋转了120°;
⊿BCD为等腰三角形.
(2)∵三角尺ABC为直角三角形,∠ACB=90°,
且∠A=30°,
∴ AB=2BC=2×6=12
∵BD=BC,A、B、D三点在一直线上,
∴AD=AB+BD=12+6=18
(3)如图,连结CE,则AC=CE
证明如下:
∵BC=BD(旋转变换的性质)
即⊿BCD为等腰三角形,
又∵∠EBD=∠ABC=60°(旋转变换的性质),
而点A、B、D在一条直线上,
∴∠CBE=180°-(∠ABC+∠EBD)
=60°=∠DBE
即BE平分等腰⊿BCD的顶角,
∴BE垂直平分底边CD(“三线合一”定理)
∴CE=DE(线段中垂线性质)
而DE=AC
故AC=CE
(也可证⊿BCE≌⊿BCA,可参照给分)
11.(2010年广东省中考拟)计算 :.
解: 原式=
=
=1
(注:只写后两步也给满分.)
12.(2010 年河南模拟)计算:
答案:-8;
13.(2010 年河南模拟)计算:-22 + ()0 + 2sin30
答案:解:原式=-4+1+1=-2
14.(2010 年河南模拟)又到了一年的春游季节,某班学生利用周末到白塔去参观“晏阳初博物馆”.下面是两位同学的对话:
甲:“我站在此处看到塔顶仰角为60°.”
乙:“我站在此处看到塔顶仰角为30°.”
甲:“我们的身高都是1.5米.”
乙:“我们相距20米.”
请你根据两位同学的对话,计算白塔的高度(精确到1米).
答案:36米
15.(2010 河南模拟)如图,有两棵树,一棵高10米,另一棵
高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树
的树梢,问小鸟至少飞行多少米?
答案:10
16.(2010年杭州月考)如图,沿江堤坝的横断面是梯形ABCD,坝顶AD=4m,坝高AE=6 m,斜坡AB的坡比,∠C=60°,求斜坡AB、CD的长。
答案:∵斜坡AB的坡比,
∵AE:BE=,又AE=6 m ∴BE=12 m
∴AB=(m)
作DF⊥BC于F,则得矩形AEFD,有DF=AE=6 m,
∵∠C=60° ∴CD=DF·sin60°= m
答:斜坡AB、CD的长分别是 m , m.
17.(2010年铁岭市加速度辅导学校)如图,为了测量电线杆的高度,在离电线杆25米的处,用高1.20米的测角仪测得电线杆顶端的仰角,求电线杆的高.(精确到0.1米)
参考数据:,,,.
解:在中,
(米)
答:电线杆的高度约为11.3米
18.(2010年广州中考数学模拟试题(四))杭州市在规划钱江新城期间,欲拆除钱塘江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
答案:由tan∠CDF==2,CF=2米.
∴DF=1米,BG=2米.
∵BD=14米,
∴BF=GC=15米.
在Rt△AGC中,由tan30°=,
∴AG=15×=≈5×1.732=8.660米.
∴AB=8.660+2=10.66米,BE=BD-ED=12米.
∵BE>AB,
∴不需要封人行道.
19.(2010年河南省南阳市中考模拟数学试题)课外实践活动中,数学老师带领学生测量学校旗杆的高度.如图,在处用测角仪(离地高度为1.5米)测得旗杆顶端的仰角为,朝旗杆方向前进23米到处,再次测得旗杆顶端的仰角为,求旗杆的高度.
答案:,,
.
.
所以DC=DE=23米.
在中,由,得
.
又FG=CA=1.5米,
因此EG=EF+FG=11.5+1.5=13(米).
答:旗杆的高度为13米.
20.(2010年河南中考模拟题2)如图所示,张伯伯利用假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6cm,微风吹来时,假设铅锤P不动,鱼漂移动了一段距离BC,且顶端恰好与水面平齐(即PA=PC),水平线L与OC的夹角a=80(点A在OC上)。请求出铅锤P处的水深h。
(参数数据:sin80≈,cos80≈,tan80 ≈)
答案:∵l∥BC ∴∠ACB==80
在Rt⊿ABC中,tan=,∴BC=≈=42
根据题意得h2+422=(h+6)2,∴h=144
单元测试
一、基础过关训练
1.从点A看点B的俯角为60°,那么从点B看点A的仰角为( )
A.60° B.30° C.60°或30° D.都不对
2.如图所示,为测一河两岸相对电线杆A,B间的距离,在距A点15m的C处(AC⊥AB)测得∠ACB=50°,则A,B间的距离为( )
A.15sin50° B.15cos50°m C.15tan50° D.15m
图4 图5
3.已知在一段坡面上,铅直高度为,坡面长为2,则坡度i=______,坡角=_____.
4.如图所示,两条宽度都为a的纸条,交叉重叠在一起,且它们的交角为,则它们重叠部分(图中阴影部分)的面积为_______.
5.如图所示,在山顶点P测得正东A,B两船的俯角分别是30°和60°,且两船相距200主,则山高PQ为多少米?(结果保留根号)
二、能力提升训练
6.某中学九(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔AB的高度.如图,在湖面上点C测得塔顶A的仰角为45°,沿直线CD向塔AB方向前进18米到达点D,测得塔顶A的仰角为60°,已知湖面低于地面1米,请你帮他们计算出塔AB的高度.(结果保留根号)
7.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级.每离台风中心距离增加20km,风力就会减弱一级,该台风中心现正在15km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变.如图,若城市所受风力达到或超过4级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由;
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
参考答案
基础过关训练
1.A 2.C 3.:3 30° 4.
5.解:设PQ=x米.
∵P处测得A,B的俯角分别为30°和60°,
∴∠A=30°,∠PBQ=60°.
∴BQ==x,AQ==x,
∴AB=AQ-BQ=x=200.
∴x=100,即PQ=100米.
能力提升训练
6.解:延长CD,交AB的延长线于点E,则∠AEC=90°,∠ACE=45°,∠ADE=60°,CD=18米.
设线段AE的长为x.
在Rt△ACE中,∵∠ACE=45°,∴CE=AE=x.
在Rt△ADE中,∵tan∠ADE=tan60°==.
∴DE=x.
∵CD=18米,且CE-DE=CD,
∴x-x=18,解得x=(27+9)米.
∵BE=1米,∴AB=AE-BE=(26+9)米.
即塔AB的高度是(26+9)米.
7.解:(1)如图,过点A作AD⊥BC,垂足为D.因为AB=220km,∠B=30°,所以AD=110km,即点A距台风中心的最近距离为20×(12-4)=160(km)时,将会受到台风的影响,故该城市会受到这次台风影响.
(2)在BC上取两点E,F,使AE=AF=160(km).当台风中心从E处移到F处时,该城市都要受到这次台风的影响.由勾股定理得DE==30(km),所以EF=60km.因为台风中心以15km/h的速度移动,所以这次台风影响该城市的持续时间为4h.
(3)当台风中心位于D处时,A市所受这次台风影响的风力最大,其最大风力为12-=6.5(级).
A
B
C
D
E
F
M
N
R
α
β
·
·
(第15题)
(第13题)
135°
A
B
C
D
h
图3
第16题图
A
C
D
B
E
F
G
A
C
D
B
E
F
G
A
B
C
D
E
F
M
N
R
α
β
第20题图2
图7
E
A
D
B
C
图8
(第23题)
_
D
_
C
_
B
_
A
i=1:
图7
_
D
_
C
_
B
_
A
i=1:
_
H
_
E
(22题图)
(第25题解答图)
第18题
A
B
E
C
D
h
37°
45°
(第25题)
A
B
C
E
D
23题图
A
B
C
M
D
G
F
E
N
A
B
C
D
C
D
N
M
A
B
第21题图
C
D
N
M
A
B
第21题图
第21题图
第21题图
D
30°
60°
A
6米
D
C
B
(第3题)
B
A
C
D
第2题图
SA
SB
第4题图
A
C
E
D
B
F
30°
45°
图2
A
B
C
图1
A
B
C
A
B
P
D
C
C
第6题图
(第7题)
A时
B时
图2
A
B
C
图1
A
B
C
(第1题)
图2
A
B
C
图1
A
B
C
y
x
E
D
O
F
y
x
E
D
O
F
x
y
O
A
B
x
y
O
A
B
x
y
O
A
B
O
A
B
D
l
A
C
C
D
E
B
F
O
B
C
A
东
西
45°
60°
A
B
O
(第3题 )
第5题图
第6题图
O
B
A
x
第7题
6m
4m
1﹕1.5
第2题图
第7题
D
C
B
A
D
C
B
A
E
2
3
1
2
3
E
B
CB
DB
AB
(第8题图)
y
x
O
A
B
第1题图
y
x
O
A
B
E
N
A′
A
B
D
C
E
第6题图
╮
60°
1.5
第7题图
D
E
F
B
C
D
E
A
B
C
D
E
A
第14题
300
600
第15题
A
B
E
C
D
(第17题)
第18题图
C
B
A
D
E
F
G
23米
第19题图
(教案+中考真题+模拟试题+单元测试)
解直角三角形及其应用
◆考点聚焦
1.掌握并灵活应用各种关系解直角三角形,这是本节重点.
2.了解测量中的概念,并能灵活应用相关知识解决某些实际问题,而在将实际问题转化为直角三角形问题时,怎样合理构造直角三角形以及如何正确选用直角三角形的边角关系是本节难点,也是中考的热点.
◆备考兵法
正确地建立解直角三角形的数学模型以及熟悉测量,航海,航空,工程等实际问题中的常用概念是解决这类问题的关键.
注意:(1)准确理解几个概念:①仰角,俯角;②坡角;③坡度;④方位角.
(2)将实际问题抽象为数学问题的关键是画出符合题意的图形.
(3)在一些问题中要根据需要添加辅助线,构造出直角三角形,从而转化为解直角三角形的问题.
◆识记巩固
1.直角三角形的边角关系:
在Rt△ABC中,∠C=90°,a,b,c分别是△ABC中∠A,∠B,∠C的对边.
(1)三边之间的关系:a2+b2=_____;
(2)两锐角之间的关系:∠A+∠B=______;
(3)直角三角形斜边上的中线等于_______;
(4)在直角三角形中,30°角所对的边等于_______.
2.解直角三角形的四种类型:
已知条件 解法
两条直角边a、b c=______,tanA=______,∠B=_______.
一条直角边a和斜边c b=______,sinA=_____,∠B=______.
一条直角边a和锐角A c=_______,b=_______,∠B=_______
斜边c和锐角A a=_______,b=_______,∠B=_______
3.坡面的_________的比叫坡度i(也叫坡比),坡度越大,坡面越陡;坡面与______的夹角,用a表示,tana=i=.
4.视线在水平线上方的角叫做_______;视线在水平线下方的角叫________.
5.方向角:正北或正南方向与目标方向线所成的_______的角叫方向角,常用“北偏东(西)××度”或“南偏东(西)××度”来描述.
识记巩固参考答案:
1.(1)c2 (2)90° (3)斜边的一半 (4)斜边的一半
2. 90°-∠A 90°-∠A
90°-∠A c·sinA 90°-∠A
3.垂直高度h和水平宽度L 水平面
4.仰角 俯角
5.小于90°
◆典例精析
例1 (2011山东威海,23,10分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠E=45°,∠A=60°,AC=10,试求CD的长.
【答案】 解:过点B作BM⊥FD于点M.
在△ACB中,∠ACB=90°, ∠A=60°,AC=10,
∴∠ABC=30°, BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=30°.
∴
在△EFD中,∠F=90°, ∠E=45°,
∴∠EDF=45°,
∴.
∴.
例2 (2011山东烟台,21,8分)综合实践课上,小明所在小组要测量护城河的宽度。如图所示是护城河的一段,两岸ABCD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)
【答案】解:过点F作FG∥EM交CD于G.
则MG=EF=20米.
∠FGN=∠α=36°.
∴∠GFN=∠β-∠FGN=72°-36°=36°.
∴∠FGN=∠GFN,
∴FN=GN=50-20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin72°=30×0.95≈29(米).
一、选择题
1. (2011湖北武汉市,10,3分)如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距离O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为
A.12秒. B.16秒. C.20秒. D.24秒.
【答案】B
2. (2011湖南衡阳,9,3分)如图所示,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长度是( )
A.10m B.10m C.15m D.5m
【答案】A
3. (2011山东东营,8,3分)河堤横断面如图所示,堤高BC=5米,迎水坡AB的坡比1:(坡比是坡面的铅直高度BC与水平宽度AC之比),则AC的长是( )
A.5米 B.10米 C.15米 D.10米
【答案】A
4. (2010湖北孝感,10,3分)如图,某航天飞船在地球表面P点的正上方A处,从A处观测到地球上的最远点Q,若∠QAP=α,地球半径为R,则航天飞船距离地球表面的最近距离AP,以及P、Q两点间的地面距离分别是( )
A. , B. ,
C. , D. ,
【答案】B
5. (2011宁波市,9,3分)如图,某游乐场一山顶滑梯的高为h,滑梯的坡角为a,那么滑梯长l为
A. B. C. D. h·sina
【答案】A
6. (2011台湾台北,34)图(十六)表示一个时钟的钟面垂直固定于水平桌面上,其中分针上有一点A,且当钟面显示3点30分时,分针垂直于桌面,A点距桌面的高度为10公分。如图(十七),若此钟面显示3点45分时,A点距桌面的高度为16公分,则钟面显示3点50分时,A点距桌面的高度为多少公分
A. B. C.18 D.19
【答案】D
7. (2011山东潍坊,10,3分)身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
同学 甲 乙 丙 丁
放出风筝线长 140m 100m 95m 90m
线与地面夹角 30° 45° 45° 60°
A.甲 B.乙 C.丙 D.丁
【答案】D
8. (2011四川绵阳10,3)周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米。假设她们的眼睛离头顶都为10cm,则 可计算出塔高约为(结果精确到0.01,参考数据:=1.414,=1.73)
A.36.21 米 B.37. 71 米
C.40. 98 米 D.42.48 米
【答案】D
二、填空题
1. (2011山东济宁,15,3分)如图,是一张宽的矩形台球桌,一球从点(点在长边上)出发沿虚线射向边,然后反弹到边上的点. 如果,.那么点与点的距离为 .
【答案】
2. (2011浙江衢州,13,4分)在一次夏令营活动中,小明同学从营地出发,要到地的北偏东60°方向的处,他先沿正东方向走了200m到达地,再沿北偏东30°方向走,恰能到达目的地(如图),那么,由此可知,两地相距 m.
【答案】200
3. (2011甘肃兰州,17,4分)某水库大坝的横断面是梯形,坝内斜坡的坡度i=1∶,坝外斜坡的坡度i=1∶1,则两个坡角的和为 。
【答案】75
4. (2011广东株洲,11,3分)如图,孔明同学背着一桶水,从山脚A出发,沿与地面成30°角的山坡向上走,送水到山上因今年春季受旱缺水的王奶奶家(B处),AB=80米,则孔明从A到B上升的高度BC是 米.
【答案】40
5. (2011浙江义乌,15,4分)右图是市民广场到解百地下通道的手扶电梯示意图.其
中AB、CD分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC=135°,BC的长约是m,则乘电梯从点B到点C上升的高度h是 ▲ m.
【答案】5
6. (2011广东茂名,13,3分)如图,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC= 米.
【答案】100
7. (2011湖北襄阳,14,3分)在207国道襄阳段改造工程中,需沿AC方向开山修路(如图3所示),为了加快施工速度,需要在小山的另一边同时施工.从AC上的一点B取∠ABD=140°,BD=1000m,∠D=50°.为了使开挖点E在直线AC上,那么DE= m.(供选用的三角函数值:sin50°=0.7660,cos50°=0.6428,tan50°=1.192)
【答案】642.8
8. (2011内蒙古乌兰察布,16,4分)某厂家新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为和,大灯A与地面离地面的距离为1m则该车大灯照亮地面的宽度BC是 m .(不考虑其它因素)
【答案】1.4
9. (2011重庆市潼南,16,4分)如图,某小岛受到了污染,污染范围可
以大致看成是以点O为圆心,AD长为直径的圆形区域,为了测量受污染的圆形
区域的直径,在对应⊙O的切线BD(点D为切点)上选择相距300米的B、C两点,分别测得∠ABD= 30°,∠ACD= 60°,则直径AD= 米.(结果精确到1米)
(参考数据: )
【答案】260
三、解答题
1. (2011浙江金华,19,6分)生活经验表明,靠墙摆放的梯子,当50°≤α≤70°(α为梯子与地面所成的角),能够使人安全攀爬,现在有一长为6米的梯子AB,试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
【解】由题意知,当α越大,梯子的顶端达到的最大高度越大.因为当50°≤α≤70°时,能够使人安全攀爬,所以当α=70°时AC最大.
在Rt△ABC中,AB=6米,α=70°,
sin70°=,即0.94≈,解得AC ≈5.6.
答:梯子的顶端能达到的最大高度AC≈5.6米.
2. (2011安徽,19,10分)如图,某高速公路建设中需要确定隧道AB的长度.已知在离地面1500m高度C处的飞机上,测量人员测得正前方A、B两点处的俯角分别为60°和45°.求隧道AB的长.
(参考数据:=1.73)
【答案】∵OA, OB=OC=1500,
∴AB=(m).
答:隧道AB的长约为635m.
3. (2011广东东莞,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即
解得
小明家到公路的距离AD的长度约为68.2m. ……………………………………………8分
4. (2011江苏扬州,25,10分)如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横断面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.
(1)求垂直支架CD的长度。(结果保留根号)
(2)求水箱半径OD的长度。(结果保留三个有效数字,参考数据:,)
【答案】解:(1)在Rt△DCE中,∠CED=60°,DE=76,
∵sin∠CED= ∴DC=DE×sin∠CED = 38 (厘米)
答:垂直支架CD的长度为38厘米。
(2)设水箱半径OD=x厘米,则OC=(38+x)厘米,AO=(150+x)厘米,
∵Rt△OAC中,∠BAC=30°
∴AO=2×OC 即:150+x=2(38+x)
解得:x=150-76≈18.52≈18.5(厘米)
答:水箱半径OD的长度为18.5厘米。
5. (2011山东德州20,10分)某兴趣小组用高为1.2米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为.测得A,B之间的距离为4米,,,试求建筑物CD的高度.
【答案】解:设建筑物CD与EF的延长线交于点G,DG=x米. …………1分
在△中,,即. …………2分
在△中,,即. …………3分
∴,.
∴ . ………5分
∴. ………6分
解方程得:=19.2. ………8分
∴ .
答:建筑物高为20.4米. ………10分
6. (2011山东威海,23,10分)一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°, ∠E=45°,∠A=60°,AC=10,试求CD的长.
【答案】 解:过点B作BM⊥FD于点M.
在△ACB中,∠ACB=90°, ∠A=60°,AC=10,
∴∠ABC=30°, BC=AC tan60°=10,
∵AB∥CF,∴∠BCM=30°.
∴
在△EFD中,∠F=90°, ∠E=45°,
∴∠EDF=45°,
∴.
∴.
7. (2011山东烟台,21,8分)综合实践课上,小明所在小组要测量护城河的宽度。如图所示是护城河的一段,两岸ABCD,河岸AB上有一排大树,相邻两棵大树之间的距离均为10米.小明先用测角仪在河岸CD的M处测得∠α=36°,然后沿河岸走50米到达N点,测得∠β=72°。请你根据这些数据帮小明他们算出河宽FR(结果保留两位有效数字).
(参考数据:sin 36°≈0.59,cos 36°≈0.81,tan36°≈0.73,sin 72°≈0.95,cos 72°≈0.31,tan72°≈3.08)
【答案】解:过点F作FG∥EM交CD于G.
则MG=EF=20米.
∠FGN=∠α=36°.
∴∠GFN=∠β-∠FGN=72°-36°=36°.
∴∠FGN=∠GFN,
∴FN=GN=50-20=30(米).
在Rt△FNR中,
FR=FN×sinβ=30×sin72°=30×0.95≈29(米).
8. (2011浙江绍兴,20,8分)为倡导“地摊生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图,车架档与的长分别为45cm,60cm,且它们相互垂直,座杆的长为20cm,点在同一条直线上,且,如图2.
(1)求车架档的长
(2)求车座点到车架档的距离.
(记过精确到1cm,参考数据:)
【答案】解(1)
=75 cm
车档架的长为75 cm
(2)过点作,垂足为点,
距离
车座点到车档架的距离是63cm
9. (2011浙江省,21,10分)图1为已建设封顶的16层楼房和其塔吊图,图2为其示意图,吊臂AB与地面EH平行,测得A点到楼顶D的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地面.
(1)求16层楼房DE的高度;
(2)若EF=16m,求塔吊的高CH 的长(精确到0.1m).
【答案】据题意得:DE=3.5×16=56,AB=EF=16
∵∠ACB=∠CBG-∠CAB=15°,
∴∠ACB =∠CAB
∴CB=AB=16. ∴CG=BC×sin30°= 8
CH=CG+HG=CG+DE+AD=8+56+5=69.
∴塔吊的高CH的长为69m.
10.(2011浙江台州,21,10分)丁丁要制作一个形如图1的风筝,想在一个矩形材料中裁剪出如图2 阴影所示的梯形翅膀,请你根据图2中的数据帮助丁丁计算出BE,CD的长度(精确到个位,)[来源:21世纪教育网]
【答案】解:在Rt△BEC中,∠BCE=30 ,EC=51,∴BE=≈30,AE=64
在Rt△AFD中,∠FAD=45 ,FD=FA=51,∴CD=64—51≈13
∴CD=13cm,BE=30cm.
11. (2011浙江丽水,19,6分)生活经验表明,靠墙摆放的梯子,当50°≤α≤70°(α为梯子与地面所成的角),能够使人安全攀爬,现在有一长为6米的梯子AB,试求能够使人安全攀爬时,梯子的顶端能达到的最大高度AC.(结果保留两个有效数字,sin70°≈0.94,sin50°≈0.77,cos70°≈0.34,cos50°≈0.64)
【解】当α=70°时,梯子顶端达到的最大高度,
∵sinα=,
∴AC = sin70°×6≈0.94×6=5.64≈5.6(米)
答:人安全攀爬梯子时,梯子的顶端达到的最大高度约5.6米.
12. (2011江西,22,9分)图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形。当点O到BC(或DE)的距离大于或等于⊙O的半径时(⊙O是桶口所在圆,半径为OA),提手才能从图甲的位置转到图乙的位置,这样的提手才合格,现在用金属材料做了一个水桶提手(如图丙A-B-C-D-E-F,C-D是弧CD,其余是线段),O是AF的中点,桶口直径AF=34cm,AB=FE=5cm,∠ABC=∠FED=149°。请通过计算判断这个水桶提手是否合格。
(参考数据:≈17.72,tan73.6°≈3.40,sin75.4°≈0.97。)
【答案】解:连结OB,过点O作OG⊥BC于点G.在Rt△ABO中,
AB=5,AO=17,∴tan∠ABO=,
∴∠ABO=73.6°,
∴∠GBO=∠ABC-∠ABO=149°-73.6°=75.4°
又∵OB=≈17.72,
∴在Rt△OBG中,OG=OB×sin∠GBO=17.72×0.97≈17.19>17.
∴水桶提手合格.
13. (2011湖南常德,24,8分)青青草原上,灰太狼每天都想着如何抓羊,而且是屡败屡试,永不言弃.(如图7所示)一天,灰太狼在自家城堡顶部A处测得懒羊羊所在地B处的俯角为60°,然后下到城堡的C处,测得B处的俯角为30°.已知AC=40米,若灰太狼以5m/s的速度从城堡底部D处出发,几秒钟后能抓到懒羊羊?(结果精确到个位)
【答案】解:在Rt△BCD中,
∵∠BCD=90°-30°=60°
∴,则
在Rt△ABD中,[来源:21世纪教育网]
∵∠ABD=60°
∴
即
∴
故约7秒钟后灰太狼能抓到懒羊羊.
14. (2011湖南邵阳,20,8分)崀山成功列入世界自然遗产名录后,景区管理部门决定在八角寨假设旅游索道设计人员为了计算索道AB(索道起点为山脚B处,终点为山顶A处)的长度,采取了如图(八)所示的测量方法。在B处测得山顶A的仰角为16°,查阅相关资料得山高AC=325米,求索道AB的长度。(结果精确到1米,参考数据sin16°≈0.28,cos16°≈0.96,tan16°≈0.29)
【答案】解:AB=AC÷sin 16°= 325÷0.28≈1161米。
15. (2011湖南益阳,18,8分)如图8,AE是位于公路边的电线杆,为了使拉线CDE不影响汽车的正常行驶,电力部门在公路的另一边竖立了一根水泥撑杆BD,用于撑起拉线.已知公路的宽AB为8米,电线杆AE的高为12米,水泥撑杆BD高
为6米,拉线CD与水平线AC的夹角为67.4°.求拉线CDE
的总长L(A、B、C三点在同一直线上,电线杆、水泥杆的大
小忽略不计).
(参考数据:,,)
【答案】解:⑴在Rt中,,
(m).
,
,,,
(m).
(m)
16. (2011江苏连云港,24,10分)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一条输水答道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5 方向,前行1200m,到达点Q处,测得A位于北偏西49 方向,B位于南偏西41 方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.
(参考数据:cos41 ≈0.75)
【答案】(1)∵B位于P点南偏东24.5 方向,∴∠BPQ=65.5 ,又∵B位于Q点南偏西41 方向, ∴∠PQB=49 , ∴∠PBQ=65.5 , ∴PQ=BQ(等角对等边),(2)∵点P处测得A在正北方向,在Rt△APQ中,,∴AQ=1600,由(1)得PQ=BQ=1200,∵在点Q处,测得A位于北偏西49 方向,B位于南偏西41 方向,∴∠AQB=90 ,在Rt△ABQ中,AB=(m).
17.
18. (2011江苏苏州,25,8分)如图,小明在大楼30米高(即PH=30米)得窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处得俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于________度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据:≈1.732).
【答案】解:(1)30.
(2)由题意得:∠PBH=60°,∠APB=45°.
∵∠ABC=30°,∴∠APB=90°.
在Rt△PHB中,PB==20,
在Rt△PBA中,AB=PB=20≈34.6.
答:A、B两点间的距离约34.6米.
19. (2011江苏宿迁,23,10分)如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取=1.732,结果精确到1m)
【答案】
解:设CE=xm,则由题意可知BE=xm,AE=(x+100)m.
在Rt△AEC中,tan∠CAE=,即tan30°=[来源:21世纪教育网]
∴,3x=(x+100)
解得x=50+50=136.6
∴CD=CE+ED=(136.6+1.5)=138.1≈138(m)
答:该建筑物的高度约为138m.
20.(2011江苏泰州,23,10分)一幢房屋的侧面外壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°.外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG ∥EH,GH=2.6cm , ∠FGB=65°.
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
【答案】解:(1)设CD与FG交于点M,由CD∥AB,∠FGB=65°,可得∠FGC=65°,又∠OCD=25°,于是在△FGC中,可得∠CFM=90°,即GF⊥OC.
(2)过点G作GN⊥HE,则GN=EF,在Rt△GHN中,
sin ∠EHG=,即GN=GH sin ∠EHG=2.6 sin 65°=2.6×0.91=2.366≈2.4cm.
21. (2011广东汕头,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即
解得
小明家到公路的距离AD的长度约为68.2m.
22. (2011山东聊城,21,8分)被誉为东昌三宝之首的铁塔,始建于北宋时期,是我市现存的最古老的建筑,铁塔由塔身和塔座两部分组成(如图①).为了测得铁塔的高度,小莹利用自制的测角仪,在C点测得塔顶E的仰角为45°,在D点测得塔顶E的仰角为60°,已知测角仪AC的高为1.6米,CD的长为6米,CD所在的水平线CG⊥EF于点G(如图②),求铁塔EF的高(结果精确到0.1米).
【答案】设EG=x米,在Rt△CEG中,∵∠ECG=45°,∴∠CEG=45°,∴∠ECG=∠CEG,∴CG=EG,=x米,在Rt△DEG中,∠EDG=60°,tan∠EDB=,∴DG=,∵CG-DG=CD=6, ∴=6,解得x=9+,∴EF=EG+FG=9++16≈158,所以铁塔高约为158米
23. (2011山东潍坊,19,9分)今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔121米,C点海拔721米.
(1)求B点的海拔;
(2)求斜坡AB的坡度.
【解】(1)如图所示,过点C作CF⊥AM,F为垂足,过点B作BE⊥AM,BD⊥CF,E、D为垂足.
∵在C点测得B点的俯角为30°,
∴∠CBD=30°,又∵BC=400米,
∴CD=400×sin30°=400×=200(米).
∴B点的海拔为721-200=521(米).
(2)∵BE=521-121=400(米),AB=1040米,
∴(米).
∴AB的坡度,所以斜坡AB的坡度为1:2.4.
24. (2011广东汕头,19,7分)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D.点C落在点E处,BF是折痕,且BF= CF =8.
(l)求∠BDF的度数;
(2)求AB的长.
【解】(1)∵BF=CF,∠C=,
∴∠FBC=,∠BFC=
又由折叠可知∠DBF=
∴∠BDF=
(2)在Rt△BDF中,
∵∠DBF=,BF=8
∴BD=
∵AD∥BC,∠A=
∴∠ABC=
又∵∠FBC=∠DBF=
∴∠ABD=
在Rt△BDA中,
∵∠AVD=,BD=
∴AB=6.
25. (2011四川广安,26,9分)某校初三课外活动小组,在测量树高的一次活动中,如图7所示,测得树底部中心A到斜坡底C的水平距离为8. 8m.在阳光下某一时刻测得1米的标杆影长为0.8m,树影落在斜坡上的部分CD= 3.2m.已知斜坡CD的坡比i=1:,求树高AB。(结果保留整数,参考数据:1.7)
【答案】解:如图,延长BD与AC的延长线交于点E,过点D作DHAE于H
∵CD=3.2 ∴DH=1.6 CH=
∵ ∴HE=1.28
∵ ∴AB=16
26. (2011四川内江,20,9分)放风筝是大家喜爱的一种运动。星期天的上午小明在大洲广场上放风筝。如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处,此时风筝线AD与水平线的夹角为30°。为了便于观察,小明迅速向前边移动边收线到达了离A处7米的B处,此时风筝线BD与水平线的夹角为45°。已知点A、B、C在同一条直线上,∠ACD=90°。请你求出小明此时所收回的风筝线的长度是多少米?(本题中风筝线均视为线段,,,最后结果精确到1米)
【答案】设BC=CD=x米,得
,解得
∴AD-BD=2x-=(米)
27. (2011四川宜宾,22,7分)如图,飞机沿水平方向(A,B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个求距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
【答案】解:此题为开放题,答案不惟一,只要方案设计合理,可参照给分
⑴如图,测出飞机在A处对山顶的俯角为,测出飞机在B处对山顶的俯角为,测出AB的距离为d,连接AM,BM.
⑵第一步,在中, ∴
第二步,在中, ∴
其中,解得.
28. (2011重庆綦江,20,6分)如图,小刚同学在綦江南州广场上观测新华书店楼房墙上的电子屏幕CD, 点A是小刚的眼睛,测得屏幕下端D处的仰角为30°,然后他正对屏幕方向前进了6米到达B处,又测得该屏幕上端C处的仰角为45°,延长AB与楼房垂直相交于点E,测得BE=21米,请你帮小刚求出该屏幕上端与下端之间的距离CD. (结果保留根号)
【答案】:解:∵∠CBE=45° CE⊥AE
∴CE=BE=21
AE=21+6=27
在Rt△ADE中,∠DAE=30°
∴DE=AE×tan30°=27×=9
∴CD=CE-DE=21-9
∴该屏幕上端与下端之间的距离CD=21-9 (米).
29. (2011江西南昌,22,9分)图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形。当点O到BC(或DE)的距离大于或等于⊙O的半径时(⊙O是桶口所在圆,半径为OA),提手才能从图甲的位置转到图乙的位置,这样的提手才合格,现在用金属材料做了一个水桶提手(如图丙A-B-C-D-E-F,C-D是弧CD,其余是线段),O是AF的中点,桶口直径AF=34cm,AB=FE=5cm,∠ABC=∠FED=149°。请通过计算判断这个水桶提手是否合格。
(参考数据:≈17.72,tan73.6°≈3.40,sin75.4°≈0.97。)
图甲 图乙 图丙
【答案】解:连结OB,过点O作OG⊥BC于点G.在Rt△ABO中,
AB=5,AO=17,∴tan∠ABO=,
∴∠ABO=73.6°,
∴∠GBO=∠ABC-∠ABO=149°-73.6°=75.4°
又∵OB=≈17.72,
∴在Rt△OBG中,OG=OB×sin∠GBO=17.72×0.97≈17.19>17.
∴水桶提手合格.
30. (2011安徽芜湖,18,8分)如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点的仰角为,再沿着的方向后退20m至处,测得古塔顶端点的仰角为.求该古塔BD的高度(,结果保留一位小数).
【答案】
解:根据题意可知:
在中,由得. …………………………2分
在中,由.得………………………4分
又∵,∴.∴(m).………………7分
答:该古塔的高度约为27.3m.
31. (2011山东济宁,18, 5分)日本福岛出现核电站事故后,我国国家海洋局高度关注事态发展,紧急调集海上巡逻的海检船,在相关海域进行现场检测与海水采样,针对核泄漏在极端情况下对海洋的影响及时开展分析评估.如图上午9时,海检船位于A处,观测到某港口城市P位于海检船的北偏西67.5°,海检船以21海里/时的速度向正北方向行驶,下午2时海检船到达B处,这时观测到城市P位于海检船的南偏西36.9°方向,求此时海检船所在B处与城市P的距离?(参考数据:sin36.9°≈,tan36.9°≈,sin67.5°≈,tan67.5°≈)
【答案】解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A=,∴AC=.…………2分
在Rt△PCB中,∵tan∠B=,∴BC=.…………4分
∵AC+BC=AB=21×5,∴,解得.
∵,∴(海里).
∴海检船所在B处与城市P的距离为100海里.………………6分
32. (2011四川成都,16,6分)如图,在亚丁湾一海域执行护航任务的我海军某军舰由东向西行驶.在航行到B处时,发现灯塔A在我军舰的正北方向500米处;当该军舰从B处向正西方向行驶至达C处时,发现灯塔A在我军舰的北偏东60°的方向.求该军舰行驶的路程.(计算过程和结果均不取近似值)
【答案】解:由题意可知,在Rt△ABC中,AB=500,∠ACB=90°-60°=30°,
∵∠ACB=,
∴BC=(),
∴该军舰行驶的路程为米.
33. (2011广东省,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即
解得
小明家到公路的距离AD的长度约为68.2m.
34. (2011广东省,19,7分)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°.折叠纸片使BC经过点D.点C落在点E处,BF是折痕,且BF= CF =8.
(l)求∠BDF的度数;
(2)求AB的长.
【解】(1)∵BF=CF,∠C=,
∴∠FBC=,∠BFC=
又由折叠可知∠DBF=
∴∠BDF=
(2)在Rt△BDF中,
∵∠DBF=,BF=8
∴BD=
∵AD∥BC,∠A=
∴∠ABC=
又∵∠FBC=∠DBF=
∴∠ABD=
在Rt△BDA中,
∵∠AVD=,BD=
∴AB=6.
35. (2011江苏淮安,23,10分)题23-1图为平地上一幢建筑物与铁塔图,题23-2图为其示意图.建筑物AB与铁塔CD都垂直于底面,BD=30m,在A点测得D点的俯角为45°,测得C点的仰角为60°.求铁塔CD的高度.
题23-1图 题23-2图
【答案】解:如图,设过点A的水平线与CD交于点E,由题意得
∠AEC=∠AED=90°,∠CAE=60°,∠DAE=45°,AE=BD=30m,
∴CD=CE+DE=AE·tan60°+AE·tan45°=30+30(m).
答:铁塔CD的高度为(30+30)m.
36. .(2011江苏南京,25,7分)如图,某数学课外活动小组测量电视塔AB的高度,他们借助一个高度为30m的建筑物CD进行测量,在点C处塔顶B的仰角为45°,在点E处测得B的仰角为37°(B、D、E三点在一条直线上).求电视塔的高度h.
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
【答案】解:在中,=.
∴EC=≈().
在中,∠BCA=45°,∴
在中,=.∴.∴().
答:电视塔高度约为120.
37. (2011四川凉山州,23,8分)在一次课题设计活动中,小明对修建一座87m长的水库大坝提出了以下方案;大坝的横截面为等腰梯形,如图,∥,坝高10m,迎水坡面的坡度,老师看后,从力学的角度对此方案提出了建议,小明决定在原方案的基础上,将迎水坡面的坡度进行修改,修改后的迎水坡面的坡度。
求原方案中此大坝迎水坡的长(结果保留根号)
如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿方向拓宽2.7m,求坝顶将会沿方向加宽多少米?
【答案】
解:⑴过点作于。
在中,∵,且。
∴,
⑵过点作于。
在中,∵,且。
∴,
如图,延长至点,至点,
连接,
∵方案修改前后,修建大坝所需土石方
总体积不变。
。即 。
。
答:坝底将会沿方向加宽。
38. (2011江苏无锡,24,9分)(本题满分9分)如图,一架飞机由A向B沿水平直线方向飞行,在航线AB的正下方有两个山头C、D。飞机在A处时,测得山头C、D在飞机前方,俯角分别为60°和30°。飞机飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方。求山头C、D之间的距离。
【答案】
解:在Rt△ABD中,∵∠BAD = 30°,∴BD = AB·tan30° = 6 × = 2.………………(2分)
∵∠BAC = 60°,∠ABC = 30°,∴∠ACB = 90°,∴BC = AB·cos30° = 6 × = 3.
…………(4分)
过点C作CE⊥BD于点E,则∠CBE = 60°,CE = BC·sin60° = .…………(6分)
∴BE = BC·cos60° = ,………………………………(7分)
DE = BD BE = 2 = .
∴在Rt△CDE中,CD = = = (km).
答:山头C、D之间的距离为(km).…………………………………………………(9分)
39. (2011湖北黄冈,21,8分)如图,防洪大堤的横断面是梯形,背水坡AB的坡比(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留三个有效数字,1.732).
【答案】 ≈36.0
40. (2011湖北黄石,22,8分)东方山是鄂东南地区的佛教胜地,月亮山是黄荆山脉第二高峰,山顶上有黄石电视塔,据黄石地理资料记载:东方山海拔453.20米,月亮山海拔442.00米。一飞机从东方山到月亮山方向水平飞行,在东方山山顶D的正上方A处测得月亮山山顶C的俯角为α,在月亮山山顶C的正上方B处测得东方山山顶D处的俯角为β,如图(7),已知tanα=0.15987,tanβ=0.15847,若飞机的飞行速度为180米/秒,则该飞机从A到B处需多少时间?(精确到0.1秒)
【答案】解:设AB=x米,根据题意得,
AD=x·tanβ=0.15847x
BC=x·tanα=0.15987x
0.15847x+453.20=0.15987x+442.00
解之得,0.0014x=11.2
x=8000
t=
t=44.4
答:该飞机从A到B处需44.4秒
41. (2011贵州贵阳,20,10分)
某过街天桥的设计图是梯形ABCD(如图所示),桥面DC与地面AB平行,DC=62米,AB=88米.左斜面AD与地面AB的夹角为23°,右斜面BC与地面AB的夹角为30°,立柱DE⊥AB于E,立柱CF⊥AB于F,求桥面DC与地面AB之间的距离.(精确到0.1米)
(第20题图)
【答案】解:在Rt△ADE中,∠A=23°,
∴AE=.
在Rt△BCF中,∠B=30°,
∴BF=.
∵DE⊥AB,CF⊥AB,AB∥CD,
∴CD=EF,DE=CF,
∴++62=88.
解得,DE≈6.4.
即桥面DC与地面AB之间的距离约为6.4米.
42. (2011江苏盐城,24,10分)如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°. 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
(结果精确到0.1cm,参考数据:≈1.732)
【答案】过点B作BF⊥CD于F,作BG⊥AD于G.
在Rt△BCF中,∠CBF=30°,∴CF=BC·sin30°= 30× =15.
在Rt△ABG中,∠BAG=60°,∴BG=AB·sin60°= 40× eq \f(,2) = 20.
∴CE=CF+FD+DE=15+20+2=17+20≈51.64≈51.6(cm)cm.
答:此时灯罩顶端C到桌面的高度CE约是51.6cm. [来源:21世纪教育网]
43. (2011广东中山,17,7分)如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路。现新修一条路AC到公路l.小明测量出∠ACD=30°,∠ABD=45°,BC=50m.请你帮小明计算他家到公路l的距离AD的长度(精确到0.1m;参考数据:)
【解】设小明家到公路的距离AD的长度为xm.
在Rt△ABD中,
∵∠ABD=,∴BD=AD=x
在Rt△ABD中,
∵∠ACD=,∴,即[来源:21世纪教育网]
解得
小明家到公路的距离AD的长度约为68.3m.
44. (2011湖北鄂州,21,8分)如图,防洪大堤的横断面是梯形,背水坡AB的坡比(指坡面的铅直高度与水平宽度的比).且AB=20 m.身高为1.7 m的小明站在大堤A点,测得高压电线杆端点D的仰角为30°.已知地面CB宽30 m,求高压电线杆CD的高度(结果保留三个有效数字,1.732).
【答案】 ≈36.0
45. (2011广东湛江24,10分)五一期间,小红到美丽的世界地质公园光岩参加社会实践活动,在景点P处测得景点B位于南偏东方向,然后沿北偏东方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.(结果精确到0.1米)
【答案】过P作,垂足为D,则,[来源:21世纪教育网21世纪教育网]
所以,且米,
所以AD=50米,
又,,所以DB=DP,而,
所以米。
46. (2011贵州安顺,21,8分)一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C,测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈)
【答案】过点C作CDAB于D ,
由题意,,设CD = BD = x米,则AD =AB+BD =(40+x)米,
在Rt中,tan=,则,解得x = 60(米).
47. (2011湖南湘潭市,19,6分)(本题满分6分)
莲城中学九年级数学兴趣小组为测量校内旗杆高度,如图,在C点测得旗杆
顶端A的仰角为30°,向前走了6米到达D点,在D点测得旗杆顶端A的仰角
为60°(测角器的高度不计).
⑴ AD=_______米;
⑵ 求旗杆AB的高度().
【答案】解:(1)6
(2)在Rt△ABD中,(米)所以旗杆AB的高度为5.19米.
48. (2011湖北荆州,21,8分)(本题满分8分)某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝,其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切,上、下桥斜面的坡度i=1:3.7,桥下水深OP=5米,水面宽度CD=24米.设半圆的圆心为O,直径AB在直角顶点M、N的连线上,求从M点上坡、过桥、下坡到N点的最短路径长.(参考数据:,,)
【答案】 解:连结OD、OE、OF,由垂径定理知:PD= 1 2 CD=12(m)
在Rt△OPD中,(m),
∴OE=OD=13m
∵tan∠EMO=i= 1: 3.7 , ≈ 1:3.7
∴∠EMO=15°
由切线性质知∠OEM=90°
∴∠EOM=75°
同理得∠NOF=75°
∴∠EOF=180°-75°×2=30°
在Rt△OEM中,tan15°=
∴EM=3.7×13=48.1(m)
又EF的弧长=30π×13÷180 =6.5(m)
∴48.1×2+6.5=102.7(m)
即从M点上坡、过桥、再下坡到N点的最短路径长为102.7米.
49.
50.
2011中考模拟分类汇编:直角三角形与勾股定理
选择题
1、(2011浙江杭州模拟14)如图折叠直角三角形纸片的直角,使点C落在斜边AB上的点E处. 已知AB=, ∠B=30°, 则DE的长是( ).
A. 6 B. 4 C. D. 2
答案:B
2.(2011湖北崇阳县城关中学模拟)直角三角形两直角边和为7,面积为6,则斜边长为( )
A. 5 B. C. 7 D.
答案:A
3.(2011年杭州市上城区一模)梯形ABCD中AB∥CD,∠ADC+∠BCD=90°,以AD、AB、BC为斜边向形外作等腰直角三角形,其面积分别是S1、S2、S3 ,
且S1 +S3 =4S2,则CD=( )
A. 2.5AB B. 3AB C. 3.5AB D. 4AB
答案:B
4.(2011年浙江省杭州市模2)直角三角形两直角边和为7,面积为6,则斜边长为( )
A. 5 B. C. 7 D.
答案:A
填空题
1、(2011年北京四中三模)如图是一个艺术窗的一部分,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5cm,则正方形A、B、C、D的面积和是 .
答案:25cm2
2.(2010-2011学年度河北省三河市九年级数学第一次教学质量检测试题)如图是两个全等的三角形纸片,其三边长之比为3:4:5,按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为SA,SB,已知SA+SB=13,则纸片的面积是 .
答案:36
3、(2011浙江杭州模拟15)如图,将含30°角的直角三角尺ABC绕点B顺时针旋转150°后得到△EBD,连结CD.若AB=4cm. 则△BCD的面积为 .
答案:
4.(2011年宁夏银川)将一副三角尺如图所示叠放在一起,若=14cm,则阴影部分的面积_________cm2.
答案:
5.(2011浙江省杭州市8模)如图1,是我国古代著名的“赵爽弦图”的示意图,它是由四全等的直角三角形围成的,若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是__________;
(第5题图)
答案:76
6、(2011年浙江杭州二模)如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米, 那么该古城墙的高度是 米.
答案:8
7、(2011年浙江杭州八模)如图,小明在A时测得某树的影长为3米,B时又测得该树的影长为12米,若两次日照的光线互相垂直,则树的高度为_____米.
答案:6
第8题图
8、(2011年浙江杭州八模)如图1,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是__________;
答案:76
9. (浙江省杭州市党山镇中2011年中考数学模拟试卷)如图,将边长为的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交于点M、N,DFAB,垂足为D,AD=1,则重叠部分的面积为 .
答案:
B组
1.( 2011年杭州三月月考)将一副三角板按如图1位置摆放,使得两块三角板的直角边AC和MD重合.已知AB=AC=8 cm,将△MED绕点A(M)逆时针旋转60°后(图2),两个三角形重叠(阴影)部分的面积是 ▲ cm2
答案:
2.(2011年重庆江津区七校联考一模)一元二次方程的两根恰好是一直角三角形的两边长,则该直角三角形的面积为 。
答案: 6或
3、(2011年浠水模拟2)如图1,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,若AC=6,BC=5,将四个 直角三角形中边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是_______________;
答案: 76
4. (2011年杭州市模拟)侧棱长为cm的直三棱柱的三个侧面面积分别为、和,则该棱柱上底面的面积为 .
答案:
5. (2011年海宁市盐官片一模)已知是直角三角形的三条边,且,斜边上的高为,则下列说法中正确的是 。(只填序号)
①;②;
③由可以构成三角形;④直角三角形的面积的最大值是.
答案:②③
6.(2011北京四中一模)在数学活动课上名师带领学生去测量河两岸A, B两处之间的距离,先从A处出发与AB成90°方向,向前走了10米到C处,在C处测得∠ACB=60°(如图所示),那么A,B之间的距离约为 米(计算结果精确到0.1米)
答案:17
7. (2011深圳市中考模拟五)等腰三角形的腰长为2,腰上的高为1,则它的底角等于 .
答案: 15°或75°
解答题
1、(2011浙江杭州模拟14)
如图,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
(1)当时,求线段的长;
(2)点M在线段AB上运动时,是否可以使得以C、P、Q为顶点的三角形为直角三角形,若可以,请直接写出t的值(不需解题步骤);若不可以,请说明理由.
(3)若△PCQ的面积为y,请求y关于出t 的函数关系式及自变量的取值范围;
答案:
解:(1)由Rt△AQM∽Rt△CAD. ……………………………………………2分
∴. 即,∴. …………………………………1分
(2)或或4. ……………………………………………3分
(3)当0<t<2时,点P在线段CD上,设直线l交CD于点E
由(1)可得. 即QM=2t.∴QE=4-2t.………………………2分
∴S△PQC =PC·QE= ………………………………………………1分
即
当>2时,过点C作CF⊥AB交AB于点F,交PQ于点H.
.
由题意得,.
∴ . ∴.
∴ . ∴.
∴ 四边形AMQP为矩形.
∴ PQ∥.CH⊥PQ,HF=AP=6- t
∴ CH=AD=HF= t-2 …………………………………………………………1分
∴S△PQC =PQ·CH= ………………………………………1分
即y=
综上所述 或y= ( 2<<6) …………………1分
2、(2011浙江杭州模拟16)
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即 “以数解形”;或者借助形的几何直观性来阐明数之间的某种关系,即 “以形助数”。
如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解: 设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)
答案:
解:(1)显然,方程x2-14x+48=0的两根为6和8, 1分
又AC>BC
∴AC=8,BC=6
由勾股定理AB=10
△ACD∽△ABC,得AC2= AD·AB
∴AD=6.4 -------------------------------2分
∵CM平分∠ACB
∴AM:MB=AC:CB
解得,AM=--------------------------------- 1分
∴MD=AD-AM=-----------------------------1分
(2)解:不访设AB=a,CD=d,AC=b,BC=c
由三角形面积公式,得AB·CD=AC·BC
2AB·CD=2AC·BC -------------------------1分
又勾股定理,得AB2=AC2+BC2
∴AB2+2AB·CD =AC2+BC2+2AC·BC(等式性质)
∴AB2+2AB·CD =(AC+BC)2----------------------1分
∴AB2+2AB·CD+CD2 >(AC+BC)2--------------------2分
∴(AB+CD) 2 >(AC+BC)2
又AB、CD、AC、BC均大于零
∴AB+CD>AC+BC即a+d>b+c--------------------1分
3. (2011年北京四中中考全真模拟17)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米?
1、探索勾股定理时,我们发现“用不同的方式表示同一图形的面积”可以解决线段和
(或差)的有关问题,这种方法称为面积法。请你运用面积法求解下列问题:在等腰三
角形ABC中,AB=AC,BD为腰AC上的高。
(1)若BD=h,M时直线BC上的任意一点,M到AB、AC的距离分别为。
若M在线段BC上,请你结合图形①证明:= h; 图①
当点M在BC的延长线上时,,h之间的关系为 .
(请直接写出结论,不必证明)
(2)如图②,在平面直角坐标系中有两条直线:y = x + 6 ; :y = -3x+6
若上的一点M到的距离是3,请你利用以上结论求解点M的坐标。
(1)证明:连结AM
①∵, EM⊥AB , MF⊥AC, BD⊥AC
∴AC.h = AB. + AC.
又∵AB = AC
∴h = + ………………………………………………2分
② - = h ………………………………………………3分
(2)由题意可知,DE = DF =10,
∴△EDF是等腰三角形。………………………………………4分
当点M在线段EF上时,依据(1)中结论,
∵h = EO=6,∴M到DF(即x轴)的距离也为3.
∴点M的纵坐标为3,此时可求得M(1,3)……………………6分
当点M在射线FE上时,依据(1)中结论
∵h = EO=6,∴M到DF(即x轴)的距离也为9.
∴点M的纵坐标为9,此时可求得M(-1,9)………………………………8分
故点M的坐标为(1,3)或(-1,9)
4、(2011年江苏盐都中考模拟)
解:原式=(4分)
5.(2011年黄冈中考调研六)(满分14分) 如图,以等边△OAB的边OB所在直线为x轴,点O为坐标原点,使点A在第一象限建立平面直角坐标系,其中△OAB边长为6个单位,点P从O点出发沿折线OAB向B点以3单位/秒的速度向B点运动,点Q从O点出发以2单位/秒的速度沿折线OBA向A点运动,两点同时出发,运动时间为t(单位:秒),当两点相遇时运动停止。
点A坐标为_____________,P、Q两点相遇时交点的坐标为________________;
当t=2时,____________;当t=3时,____________;
设△OPQ的面积为S,试求S关于t的函数关系式;
当△OPQ的面积最大时,试求在y轴上能否找一点M,使得以M、P、Q为顶点的三角形是Rt△,若能找到请求出M点的坐标,若不能找到请简单说明理由。
答案.
A点坐标为、交点坐标为(
当t=2时,; 当t=3时,
对(3)中的分段函数进行计算后得知当t=2,S有最大值,此时P与A重合,OP=6,OQ=4,过P作PC⊥OB于C点,计算得OC=3,AC=,CQ=1,PQ=
如图①,过P作PM⊥PQ交y轴于M点,过M作MN⊥AC于N,则MN=OC=3,易得Rt△PMN∽△QPC,有即,得PN=,MO=NC=故M点坐标为
过Q作MQ⊥PQ交y轴于M点,通过△MOQ∽△QCP,求得M坐标为
以PQ为直径作⊙D,则⊙D半径r为,再过P作PE⊥y轴于E点,过D作DF⊥y轴于F点,由梯形中位线求得DF=,显然r<DF,故⊙D与y同无交点,那么此时在y轴上无M点使得△MPQ为直角三角形.
综上所述,满足要求的M点或
6. (2011浙江省杭州市8模)(本题满分8分)某商场为了迎接“六一”儿童节的到来,制造了一个超大的“不倒翁”。小灵对“不倒翁”很感兴趣,原来“不倒翁”的底部是由一个空心的半球做成的,并在底部的中心(即图中的C处)固定一个重物,再从正中心立起一根杆子,在杆子上作些装饰,在重力和杠杆的作用下,“不倒翁”就会左摇右晃,又不会完全倒下去。小灵画出剖面图,进行细致研究:圆弧的圆心为点O,过点O的木杆CD长为260㎝,OA、OB为圆弧的半径长为90㎝(作为木杆的支架),且OA、OB关于CD对称,弧AB的长为30㎝。当木杆CD向右摆动使点B落在地面上(即圆弧与直线l相切于点B)时,木杆的顶端点D到直线l的距离DF是多少㎝?
(第6题)
解:由弧AB的长可得,∠AOB=60°,
从而∠BOE=∠COB=30°,(2分)
∵OB=90cm,
∴OE=cm,(2分)
∴DE=170+ cm, (2分)[来源:21世纪教育网21世纪教育网]
∴DF=180+ cm (2分)
7.(2011广东南塘二模)如图,在小山的东侧A处有一热气球,以每分钟30m
的速度沿着仰角为60°的方向上升,20分钟后升到B处,这时
气球上的人发现在A的正西方向俯角为45°的C处有一着火点,
求气球的升空点A与着火点C的距离(结果保留根号).
答案:过B作BD⊥CA于D,则AB=600m,AD=300m,BD=CD=300m,CA=300(-1)m。
8.(2011深圳市全真中考模拟一)△ABC中,BC=,AC=,AB=c.若,如图l,根据勾股定理,则。若△ABC不是直角三角形,如图2和图3,请你类比勾股定理,试猜想与的关系,并证明你的结论.
答案:解:若△ABC是锐角三角形,则有 …… (1分)
若△ABC是钝角三角形,为钝角,则有。 (2分)
当△ABC是锐角三角形时,
证明:过点A作ADBC,垂足为D,设CD为,则有BD=……(3分)
根据勾股定理,得
即。
∴…………………………(5分)
∵,
∴。
∴。…………………………(6分)
当△ABC是钝角三角形时,
证明:过B作BDAC,交AC的延长线于D。
设CD为,则有…………………………(7分)
根据勾股定理,得.
即。…………………………(9分)
∵,
∴,
∴。…………………………(10分)
解直角三角形
一、选择题
1.(2010年教育联合体)在△ABC中,已知AB=5,AC=3,BC=4,则下列结论中正确的是( )
A.sinA= B.cosB= C.tanA= D.tanB=
答案:A
2.(2010年安徽省模拟)如图,△ABC为边长是5的等边三角形,点E在AC边上,点F在AB边上,ED⊥BC,且ED=AE,DF=AF,则CE的长是( )
A. B.
C. D.
答案:D
3.(2010年北京市朝阳区模拟)正方形网格中,如图放置,则的值为( )
A. B.2 C. D.
答案:D
4.(2010年三亚市月考)在△ABC中,∠C=90°,a、b、c分别为∠A、∠B、∠C的对边,下列各式成立的是( )
A. b=a·sinB B. a=b·cosB C. a=b·tanB D. b=a·tanB
答案D
5.(2010年聊城冠县实验中学二模)正方形网格中,∠AOB如下图放置,则
tan∠AOB的值为( )
A.2 B. C. D.
答案A
6.(2010年聊城冠县实验中学二模)如下图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①BD=BE,②∠A=∠BHE,③AB=BH,④△BHD∽△BDG。其中正确的结论是( )
A.①②③④ B.①②③ C.①②④ D.②③④
答案B
7.(2010年江西南昌一模)如图,点A的坐标为(-1,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为
A.(-,-)
B.(,)
C.(-,-)
D.(0,0)
答案:A
8.(2010年武汉市中考拟)如图,AB为⊙O的直径,CA切⊙O于A,
CB交⊙O于D,若CD=2,BD=6,则sinB=( )
A. B. C. D.
答案:A
9.(2010年厦门湖里模拟)在Rt△ABC中,∠C=90°,AB=13,BC=5,则 ( )
A. B. C. D.
答案:B
10.(2010年杭州月考)已知在中,,则的值为( )
A. B. C. D.
答案:A
11.(2010年天水模拟)如图为了测量某建筑物AB的高度,在平地上C 处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D 处,在D处测得建筑物项端A的仰角为45°,则建筑物AB的高度等于( )
A.6()m B.6()m
C.12()m D.12()m
答案:A
12.(2010年广州中考数学模拟试题一)已知α为等边三角形的一个内角,则cosα等于( )
A. B. C. D.
答:A
13.( 2010年山东菏泽全真模拟1) 王英同学从A地沿北偏西60 方向走100m到B地,再从B地向正南方向走200m到C地,此时王英同学离A地 ( )
A.m B.100 m C.150m D.m
答案:D
14.(2010年江苏省泰州市济川实验初中中考模拟题)如图,△ABC的顶点都是正方形网格中的格点,则cos∠ABC的值为( )
A. eq \f(3,10) B. eq \f(2,5) C. eq \f(,2) D.
二、填空题
1.(2010年安徽省模拟)化简 .
答案:
2.(2010年三亚市月考).如图,铁路的路基的横断面为等腰梯形,其腰的坡度为1:1.5,上底宽为6m,路基高为4m,则路基的下底宽为 .
答案: 18m ;
3.(2010年天水模拟)如图,某公园入口处原有三阶台阶,每级台阶高为20cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡的坡度i=,则AC的长度是 .
答案:240cm
4.(2010年重庆市綦江中学模拟1)如图,身高1.6m的小丽用一个两锐角分别为30°和60°的三角尺测量一棵树的高度,已知她与树之间的距离为6m,那么这棵树高大约为(结果精确到0.1m,其中小丽眼睛距离地面高度近似为身高) .
答案: 5.1m
5.(2010年江西南昌一模)如图,在正方形网格中,∠AOB的正切值是
答案:
6.(2010年山东新泰)若△ABC中,∠C=90°,AC:BC=3:4,那么sinA= .
答案:
7.(2010年天津市中考模拟)如图,有一个边长为5的正方形纸片,要将其剪拼成边长分别为的两个小正方形,使得.①的值可以是________(写出一组即可);②请你设计一种具有一般性的裁剪方法,在图中画出裁剪线,并拼接成两个小正方形,同时说明该裁剪方法具有一般性:
__________________________________________
_________________________________________
_________________________________________
答案:①3,4(提示:答案不惟一);
②裁剪线及拼接方法如图所示:图中的点可以是以为直径的半圆上的任意一点(点除外).的长分别为两个小正方形的边长
8.(2010年辽宁抚顺中考模拟)将一个含30°角的三角板和一个含45°角的三角板如图摆放,与完全重合,,,则 .
答案:
9.(2010年江西省统一考试样卷)比较大小:sin33°+cos33° 1.(可用计算器辅助)
答案:>.
10.(2010年河南中考模拟题1)
答案:
三、解答题
1.(2010年湖里区二次适应性考试))如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
(1)求抛物线的解析式;
(2)在抛物线上求点M,使△MOB的面积是△AOB面积的3倍;
(3)连结OA,AB,在x轴下方的抛物线上是否存在点N,使△OBN与△OAB相似?若存在,求出N点的坐标;若不存在,说明理由.
答案:(1)由题意,可设抛物线的解析式为,
∵抛物线过原点,
∴, .
∴抛物线的解析式为.
(2)和所求同底不等高,,
∴的高是高的3倍,即M点的纵坐标是.
∴,即.
解之,得 ,.
∴满足条件的点有两个:,.
(3)不存在.
由抛物线的对称性,知,.
如图,若与相似,必有.
设交抛物线的对称轴于点,显然.
∴直线的解析式为.
由,得,.
∴ .
过作轴,垂足为.在中,,,
∴.
又OB=4,
∴,,与不相似.
同理,在对称轴左边的抛物线上也不存在符合条件的点.
所以在该抛物线上不存在点N,使与相似.
2.(2010年北京市朝阳区模拟) .
解:原式=
=
3.(2010年北京市朝阳区模拟)小明站在A处放风筝,风筝飞到C处时的线长为20米,这时测得∠CBD=60°,若牵引底端B离地面1.5米,求此时风筝离地面高度。(计算结果精确到0.1米,)
解:在Rt△BCD中,CD=BC×sin60°=20×
又∵DE=AB=1.5
∴CE=CD+DE=(米)
答:此时风筝离地面的高度约是18.8米.
4.(2010年教育联合体)计算:
原式= =2
5.(2010年安徽省模拟)为测量大楼CD的高度,某人站在A处测得楼顶的仰角为450,前进20m后到达B处测得楼顶的仰角为600,求大楼 CD的高度。
解:如图,依题意得∠CBD=600 , ∠CDB=900,设BD=x m,则AD=(20+x) m
CD= m
在Rt△ACD中,∠CAD=450 , ∠CDA=900
∴AD=CD
∴20+x=
∴x=10(+1)
∴CD=x=(30+) m ,即楼高为(30+) m
6.(2010年三亚市月考) 如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,试求该塔的高度。(≈1.41,≈1.73)
解:由题意可知 CD=10米,BD=1.5米,∠ACD=60°.
在Rt△ACD中,AD=CDtan60°= 10
∴AB=AD+DB=10 + 1.5 ≈10×1.73 + 1.5 =18.8(米)
答:该塔的高度是18.8米
7.(2010年聊城冠县实验中学二模)九年级甲班数学兴趣小组组织社会实践活动,目的是测量一山坡的护坡石坝高度及石坝与地面的倾角.
(1)如上图1,小明所在的小组用一根木条EF斜靠在护坡石坝上,使得BF与BE的长度相等,如果测量得到∠EFB=36°,那么的度数是___________;
(2)如上图2,小亮所在的小组把一根长为5米的竹竿AG斜靠在石坝旁,量出竿长1米时离地面的高度为0.6米,请你求出护坡石坝的垂直高度AH;
(3)全班总结了各组的方法后,设计了如上图3方案:在护坡石坝顶部的影子处立一根长为米的杆子PD,杆子与地面垂直,测得杆子的影子长为米,点P到护坡石坝底部B的距离为米,如果利用(1)得到的结论,请你用表示出护坡石坝的垂直高度AH。(,,)
解.(1)72°
(2)3米
(3)
8.(2010年年广州市中考六模)、如图,某中学科学楼高15米,计划在科学楼正北方向的同一水平地上建一幢宿舍楼,第一层是高2.5米的自行车场,第二层起为宿舍。已知该地区一年之中“冬至”正午时分太阳高度最低,此时太阳光线AB的入射角∠ABD=55°,为使第二层起能照到阳光,两楼间距EF至少是多少米?(精确到0.1米)。
(参考数据:tan55°=1.4281,tan35°=0.7002)。
答案:
由矩形BCEF得到CE=BF,BC=EF [来源:21世纪教育网]
得到∠CAB=55o
得到BC=ACtan55o BC=17.9米 作答
9.(2010年广州市中考七模)、如图,某电信公司计划修建一条连接B、C两地的电缆。测量人员在山脚A点测得B、C两地的仰角分别为30°、45°,在B处测得C地的仰角为60°,已知C地比A地高200m,求电缆BC的长(结果保留根号).
解:画BE、CF均垂直于AM,垂足分别为E、F;画BD⊥CF于D.
则四边形BEFD是矩形. 设BD=x,由题意得
AF=CF=200,EF=BD=x,AE=200- x
∵∠CBD=60°,
∴CD=tan60°·BD=x,BE=DF=200-x
∵= tan∠BAE= tan30°=,
即=,
解得x =,
∴BC=2x= (m)
10.(2010年广东省中考拟)如图所示,把一个直角三角尺ABC绕着60°角的顶点B顺时针旋转,使得点C与AB的延长线上的点D重合,已知BC=6.
(1)三角尺旋转了多少度?连结CD,试判断⊿BCD的形状;
(2)求AD的长;
(3)连结CE,试猜想线段AC与CE的大小关系,并证明你的结论.
解:(1)三角尺旋转了120°;
⊿BCD为等腰三角形.
(2)∵三角尺ABC为直角三角形,∠ACB=90°,
且∠A=30°,
∴ AB=2BC=2×6=12
∵BD=BC,A、B、D三点在一直线上,
∴AD=AB+BD=12+6=18
(3)如图,连结CE,则AC=CE
证明如下:
∵BC=BD(旋转变换的性质)
即⊿BCD为等腰三角形,
又∵∠EBD=∠ABC=60°(旋转变换的性质),
而点A、B、D在一条直线上,
∴∠CBE=180°-(∠ABC+∠EBD)
=60°=∠DBE
即BE平分等腰⊿BCD的顶角,
∴BE垂直平分底边CD(“三线合一”定理)
∴CE=DE(线段中垂线性质)
而DE=AC
故AC=CE
(也可证⊿BCE≌⊿BCA,可参照给分)
11.(2010年广东省中考拟)计算 :.
解: 原式=
=
=1
(注:只写后两步也给满分.)
12.(2010 年河南模拟)计算:
答案:-8;
13.(2010 年河南模拟)计算:-22 + ()0 + 2sin30
答案:解:原式=-4+1+1=-2
14.(2010 年河南模拟)又到了一年的春游季节,某班学生利用周末到白塔去参观“晏阳初博物馆”.下面是两位同学的对话:
甲:“我站在此处看到塔顶仰角为60°.”
乙:“我站在此处看到塔顶仰角为30°.”
甲:“我们的身高都是1.5米.”
乙:“我们相距20米.”
请你根据两位同学的对话,计算白塔的高度(精确到1米).
答案:36米
15.(2010 河南模拟)如图,有两棵树,一棵高10米,另一棵
高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树
的树梢,问小鸟至少飞行多少米?
答案:10
16.(2010年杭州月考)如图,沿江堤坝的横断面是梯形ABCD,坝顶AD=4m,坝高AE=6 m,斜坡AB的坡比,∠C=60°,求斜坡AB、CD的长。
答案:∵斜坡AB的坡比,
∵AE:BE=,又AE=6 m ∴BE=12 m
∴AB=(m)
作DF⊥BC于F,则得矩形AEFD,有DF=AE=6 m,
∵∠C=60° ∴CD=DF·sin60°= m
答:斜坡AB、CD的长分别是 m , m.
17.(2010年铁岭市加速度辅导学校)如图,为了测量电线杆的高度,在离电线杆25米的处,用高1.20米的测角仪测得电线杆顶端的仰角,求电线杆的高.(精确到0.1米)
参考数据:,,,.
解:在中,
(米)
答:电线杆的高度约为11.3米
18.(2010年广州中考数学模拟试题(四))杭州市在规划钱江新城期间,欲拆除钱塘江岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2(即tan∠CDF=2),岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
答案:由tan∠CDF==2,CF=2米.
∴DF=1米,BG=2米.
∵BD=14米,
∴BF=GC=15米.
在Rt△AGC中,由tan30°=,
∴AG=15×=≈5×1.732=8.660米.
∴AB=8.660+2=10.66米,BE=BD-ED=12米.
∵BE>AB,
∴不需要封人行道.
19.(2010年河南省南阳市中考模拟数学试题)课外实践活动中,数学老师带领学生测量学校旗杆的高度.如图,在处用测角仪(离地高度为1.5米)测得旗杆顶端的仰角为,朝旗杆方向前进23米到处,再次测得旗杆顶端的仰角为,求旗杆的高度.
答案:,,
.
.
所以DC=DE=23米.
在中,由,得
.
又FG=CA=1.5米,
因此EG=EF+FG=11.5+1.5=13(米).
答:旗杆的高度为13米.
20.(2010年河南中考模拟题2)如图所示,张伯伯利用假日在某钓鱼场钓鱼,风平浪静时,鱼漂露出水面部分AB=6cm,微风吹来时,假设铅锤P不动,鱼漂移动了一段距离BC,且顶端恰好与水面平齐(即PA=PC),水平线L与OC的夹角a=80(点A在OC上)。请求出铅锤P处的水深h。
(参数数据:sin80≈,cos80≈,tan80 ≈)
答案:∵l∥BC ∴∠ACB==80
在Rt⊿ABC中,tan=,∴BC=≈=42
根据题意得h2+422=(h+6)2,∴h=144
单元测试
一、基础过关训练
1.从点A看点B的俯角为60°,那么从点B看点A的仰角为( )
A.60° B.30° C.60°或30° D.都不对
2.如图所示,为测一河两岸相对电线杆A,B间的距离,在距A点15m的C处(AC⊥AB)测得∠ACB=50°,则A,B间的距离为( )
A.15sin50° B.15cos50°m C.15tan50° D.15m
图4 图5
3.已知在一段坡面上,铅直高度为,坡面长为2,则坡度i=______,坡角=_____.
4.如图所示,两条宽度都为a的纸条,交叉重叠在一起,且它们的交角为,则它们重叠部分(图中阴影部分)的面积为_______.
5.如图所示,在山顶点P测得正东A,B两船的俯角分别是30°和60°,且两船相距200主,则山高PQ为多少米?(结果保留根号)
二、能力提升训练
6.某中学九(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔AB的高度.如图,在湖面上点C测得塔顶A的仰角为45°,沿直线CD向塔AB方向前进18米到达点D,测得塔顶A的仰角为60°,已知湖面低于地面1米,请你帮他们计算出塔AB的高度.(结果保留根号)
7.台风是一种自然灾害,它以台风中心为圆心在周围数十千米范围内形成气旋风暴,有极强的破坏力.据气象观测,距沿海某城市A的正南方向220km的B处有一台风中心,其中心最大风力为12级.每离台风中心距离增加20km,风力就会减弱一级,该台风中心现正在15km/h的速度沿北偏东30°方向往C移动,且台风中心风力不变.如图,若城市所受风力达到或超过4级,则称为受台风影响.
(1)该城市是否会受到这次台风的影响?请说明理由;
(2)若会受台风影响,那么台风影响该城市的持续时间有多长?
(3)该城市受到台风影响的最大风力为几级?
参考答案
基础过关训练
1.A 2.C 3.:3 30° 4.
5.解:设PQ=x米.
∵P处测得A,B的俯角分别为30°和60°,
∴∠A=30°,∠PBQ=60°.
∴BQ==x,AQ==x,
∴AB=AQ-BQ=x=200.
∴x=100,即PQ=100米.
能力提升训练
6.解:延长CD,交AB的延长线于点E,则∠AEC=90°,∠ACE=45°,∠ADE=60°,CD=18米.
设线段AE的长为x.
在Rt△ACE中,∵∠ACE=45°,∴CE=AE=x.
在Rt△ADE中,∵tan∠ADE=tan60°==.
∴DE=x.
∵CD=18米,且CE-DE=CD,
∴x-x=18,解得x=(27+9)米.
∵BE=1米,∴AB=AE-BE=(26+9)米.
即塔AB的高度是(26+9)米.
7.解:(1)如图,过点A作AD⊥BC,垂足为D.因为AB=220km,∠B=30°,所以AD=110km,即点A距台风中心的最近距离为20×(12-4)=160(km)时,将会受到台风的影响,故该城市会受到这次台风影响.
(2)在BC上取两点E,F,使AE=AF=160(km).当台风中心从E处移到F处时,该城市都要受到这次台风的影响.由勾股定理得DE==30(km),所以EF=60km.因为台风中心以15km/h的速度移动,所以这次台风影响该城市的持续时间为4h.
(3)当台风中心位于D处时,A市所受这次台风影响的风力最大,其最大风力为12-=6.5(级).
A
B
C
D
E
F
M
N
R
α
β
·
·
(第15题)
(第13题)
135°
A
B
C
D
h
图3
第16题图
A
C
D
B
E
F
G
A
C
D
B
E
F
G
A
B
C
D
E
F
M
N
R
α
β
第20题图2
图7
E
A
D
B
C
图8
(第23题)
_
D
_
C
_
B
_
A
i=1:
图7
_
D
_
C
_
B
_
A
i=1:
_
H
_
E
(22题图)
(第25题解答图)
第18题
A
B
E
C
D
h
37°
45°
(第25题)
A
B
C
E
D
23题图
A
B
C
M
D
G
F
E
N
A
B
C
D
C
D
N
M
A
B
第21题图
C
D
N
M
A
B
第21题图
第21题图
第21题图
D
30°
60°
A
6米
D
C
B
(第3题)
B
A
C
D
第2题图
SA
SB
第4题图
A
C
E
D
B
F
30°
45°
图2
A
B
C
图1
A
B
C
A
B
P
D
C
C
第6题图
(第7题)
A时
B时
图2
A
B
C
图1
A
B
C
(第1题)
图2
A
B
C
图1
A
B
C
y
x
E
D
O
F
y
x
E
D
O
F
x
y
O
A
B
x
y
O
A
B
x
y
O
A
B
O
A
B
D
l
A
C
C
D
E
B
F
O
B
C
A
东
西
45°
60°
A
B
O
(第3题 )
第5题图
第6题图
O
B
A
x
第7题
6m
4m
1﹕1.5
第2题图
第7题
D
C
B
A
D
C
B
A
E
2
3
1
2
3
E
B
CB
DB
AB
(第8题图)
y
x
O
A
B
第1题图
y
x
O
A
B
E
N
A′
A
B
D
C
E
第6题图
╮
60°
1.5
第7题图
D
E
F
B
C
D
E
A
B
C
D
E
A
第14题
300
600
第15题
A
B
E
C
D
(第17题)
第18题图
C
B
A
D
E
F
G
23米
第19题图
同课章节目录
