分式方程
图片预览






文档简介
(共17张PPT)
分式方程(1)
义务教育课程标准实验教科书
数
学
1、理解分式方程的意义以及分式方程化简;
2、熟练地求解分式方程,并会验根。
学
习
目
标
自
学
指
导
1、阅读:P26——P29
2、思考:
(1)什么叫分式方程?
(2)把分式方程化成整式方程的关键是什么?
(3)解分式方程应怎样检验?
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少
设江水的水流速度为 v千米/时,
轮船顺流航行的速度为_____千米/时,
逆流航行的速度为_____千米/时,
顺流航行100千米所用时间为______小时,
逆流航行60千米所用时间为______小时.
(20+v)
(20-v)
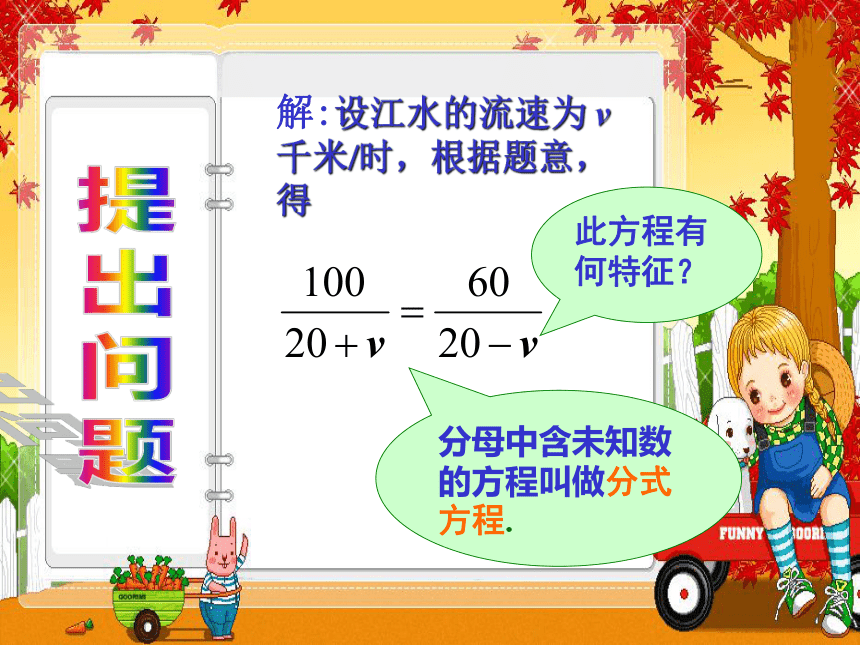
解:设江水的流速为 v 千米/时,根据题意,得
分母中含未知数的方程叫做分式方程.
此方程有何特征?
下列关于x的方程中,其中哪几个是分式方程
分母中是否含有未知数
各分母的最简公分母
你敢应战吗?
将分式方程转化为整式方程
解得: v = 5
检验:将v=5代入原方程,左边=4=右边,因些v=5是分式方程的解.
你敢应战吗?
两边同乘以 得:
各分母的
最简公分母
解分式方程:
方程两边同乘最简公分母
得整式方程
解得
检验: 将 代入原分式方程检验发现分母
相应的分式无意义,因此x=5不是分式方程的解,此分式方程无解
为什么会产生增根
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
因此解分式方程可能产生增根,解分式方程必须检验
解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
4、写出原方程的解.
解分式方程的思路是:
分式方程
整式方程
去分母
解方程
解:方程两边同乘 x ( x – 3 ) , 约去分母,得
2x=3 x - 9
解得
x = 9
检验: x = 9时x ( x – 3 )≠0
∴9是原分式方程的解.
例 1
解方程:
随堂练习
拓展延伸:
解关于x的方程 产生增根,则常数m的值等于( )
(A)-2 (B)-1 (C ) 1 (D) 2
x-3
x-1
x-1
m
=
1、解分式方程的思路是:
分式方程
整式方程
去分母
2、解分式方程的一般步骤:
一化二解三检验
(1)课本
P32 习题16.3
第 1题中的
(1)~(4)
(2)预习
分式方程的应用
再见
分式方程(1)
义务教育课程标准实验教科书
数
学
1、理解分式方程的意义以及分式方程化简;
2、熟练地求解分式方程,并会验根。
学
习
目
标
自
学
指
导
1、阅读:P26——P29
2、思考:
(1)什么叫分式方程?
(2)把分式方程化成整式方程的关键是什么?
(3)解分式方程应怎样检验?
一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少
设江水的水流速度为 v千米/时,
轮船顺流航行的速度为_____千米/时,
逆流航行的速度为_____千米/时,
顺流航行100千米所用时间为______小时,
逆流航行60千米所用时间为______小时.
(20+v)
(20-v)
解:设江水的流速为 v 千米/时,根据题意,得
分母中含未知数的方程叫做分式方程.
此方程有何特征?
下列关于x的方程中,其中哪几个是分式方程
分母中是否含有未知数
各分母的最简公分母
你敢应战吗?
将分式方程转化为整式方程
解得: v = 5
检验:将v=5代入原方程,左边=4=右边,因些v=5是分式方程的解.
你敢应战吗?
两边同乘以 得:
各分母的
最简公分母
解分式方程:
方程两边同乘最简公分母
得整式方程
解得
检验: 将 代入原分式方程检验发现分母
相应的分式无意义,因此x=5不是分式方程的解,此分式方程无解
为什么会产生增根
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
因此解分式方程可能产生增根,解分式方程必须检验
解分式方程的一般步骤
1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程.
2、解这个整式方程.
3、 把整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解.
4、写出原方程的解.
解分式方程的思路是:
分式方程
整式方程
去分母
解方程
解:方程两边同乘 x ( x – 3 ) , 约去分母,得
2x=3 x - 9
解得
x = 9
检验: x = 9时x ( x – 3 )≠0
∴9是原分式方程的解.
例 1
解方程:
随堂练习
拓展延伸:
解关于x的方程 产生增根,则常数m的值等于( )
(A)-2 (B)-1 (C ) 1 (D) 2
x-3
x-1
x-1
m
=
1、解分式方程的思路是:
分式方程
整式方程
去分母
2、解分式方程的一般步骤:
一化二解三检验
(1)课本
P32 习题16.3
第 1题中的
(1)~(4)
(2)预习
分式方程的应用
再见
