对数函数
图片预览


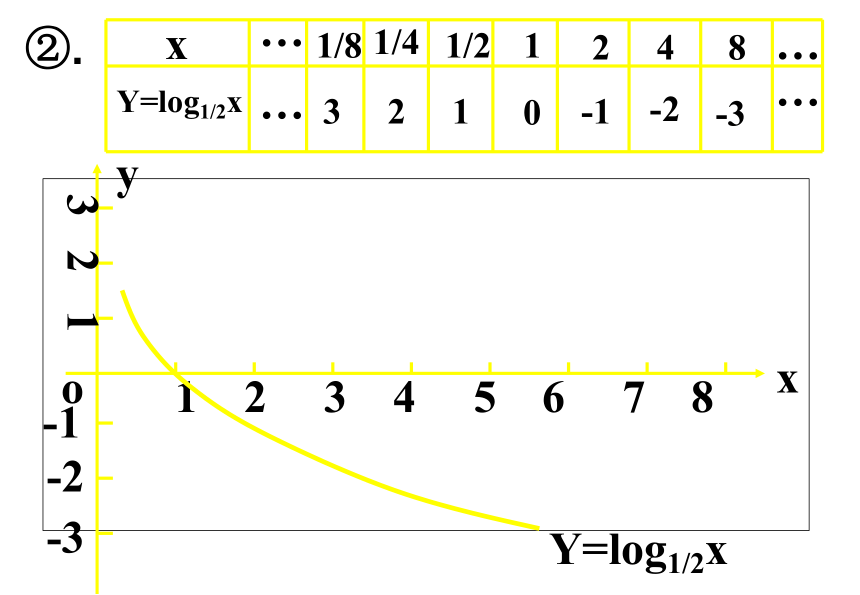

文档简介
(共25张PPT)
对数函数的图像和性质
一.复习对数函数的概念
定义: 函数 y = loga x (a>0,且a≠ 1 )
叫做对数函数.,其中 x是自变量,
函数定义域是( 0 , +∞)。
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0定 义 域 :
值 域 :
恒 过 点:
在 R 上是单调
在 R 上是单调
a>1
0R
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
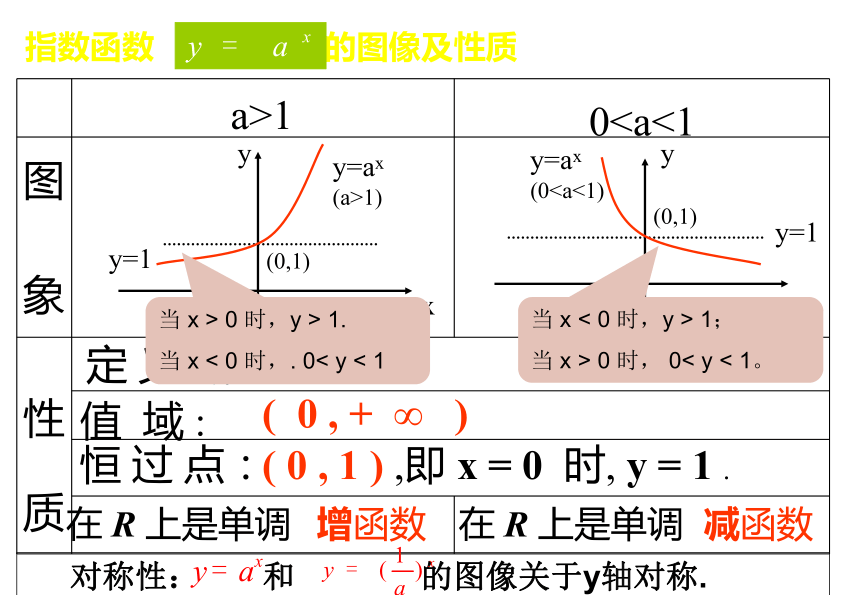
指数函数 的图像及性质
当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
对称性: 和 的图像关于y轴对称.
x
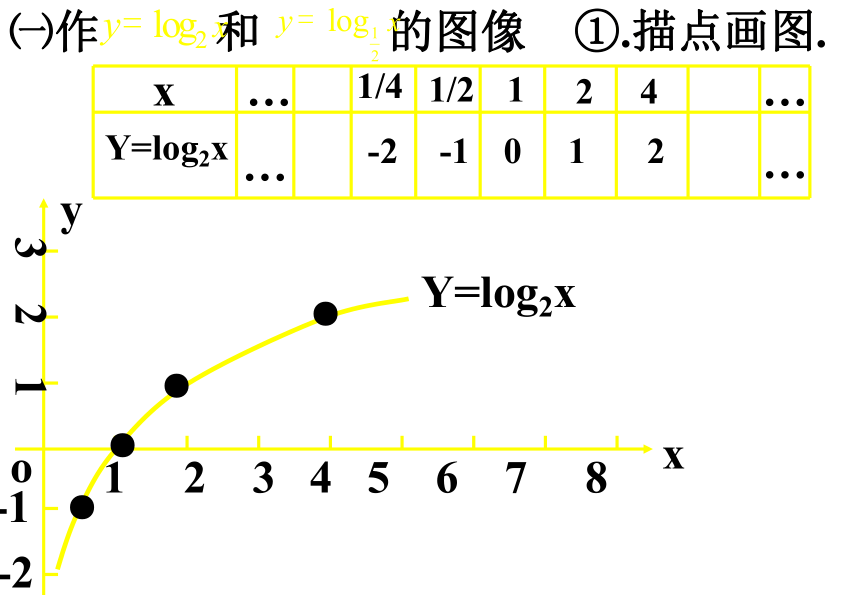
Y=log2x
…
…
1/4
1/2
1
2
4
…
…
-2
-1
0
1
2
x
y
o
1 2 3 4 5 6 7 8
1
2
3
-1
-2
-3
Y=log2x
①.描点画图.
●
●
●
●
㈠作 和 的图像
x
Y=log1/2x
…
…
…
…
-3
1/8
1/4
1/2
1
2
4
8
-2
-1
0
1
2
3
x
y
o
1 2 3 4 5 6 7 8
1
2
3
-1
-2
-3
Y=log1/2x
②.
O
X
Y
1
2
3
4
5
6
7
8
9
1
2
3
-1
-2
-3
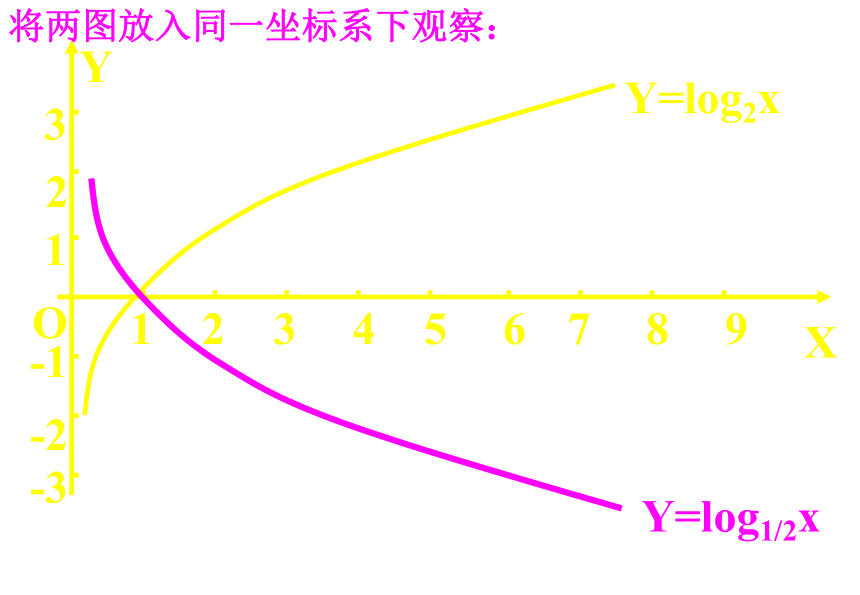
Y=log2x
Y=log1/2x
将两图放入同一坐标系下观察:
三.对数函数的性质:
现在我们同样利用描点法在同一坐标系
下作出 和
的图像,观察图像并
归纳总结性质.
4
3
2
1
-1
-2
-3
2
4
6
8
10
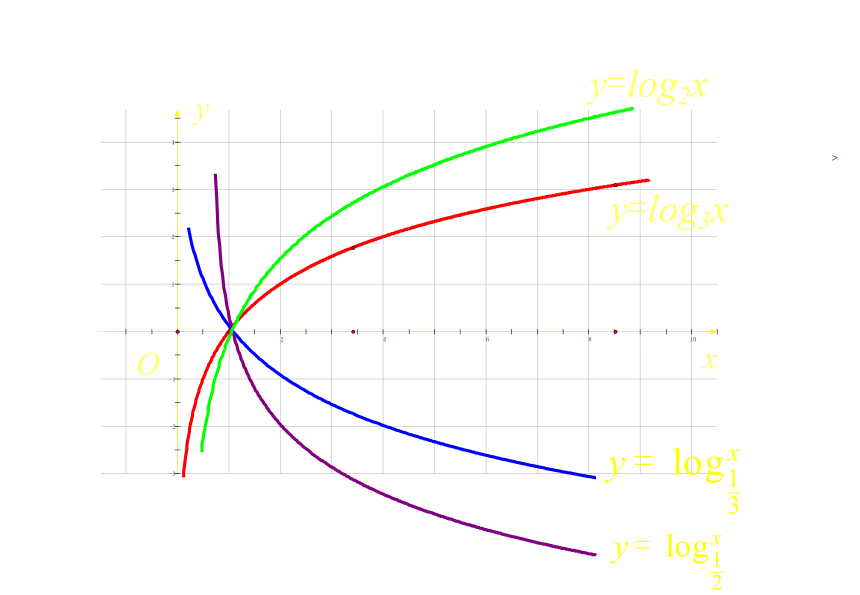
y=log2x
y=log3x
x
y
O
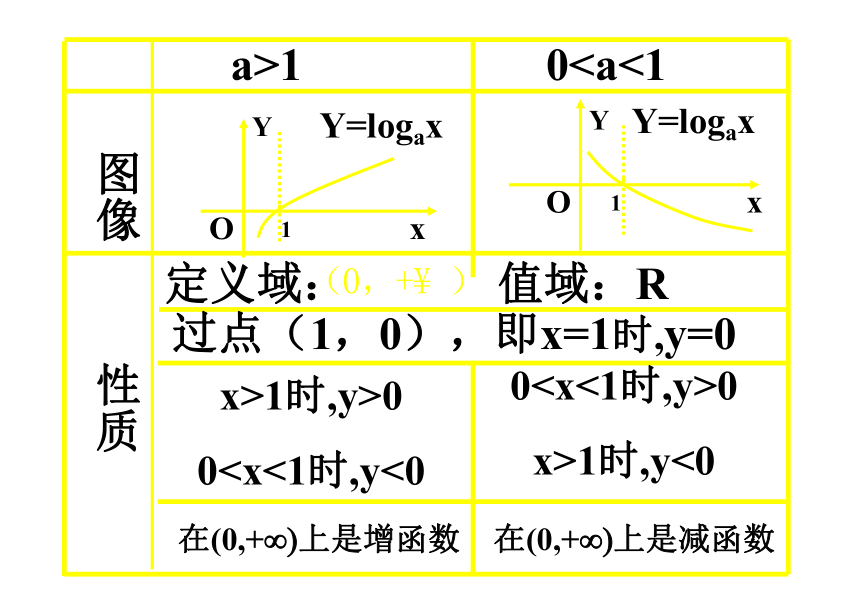
a>1
0图像
性质
定义域: 值域:R
过点(1,0),即x=1时,y=0
x>1时,y>0
000
x>1时,y<0
在(0,+ 上是增函数
在(0,+ 上是减函数
x
1
Y
O
Y=logax
x
Y
O
1
Y=logax
4
3
2
1
-1
-2
-3
2
4
6
8
10
y=log2x
y=log3x
x
y
O
总结其它性质:
(1)y=logax (a>0,且a≠ 1 )与y=log1/ax (a>0,且a≠ 1 ) 的图像关于x轴对称。
(2)对数函数是非奇非偶函数。
考虑:根据作出的图像,还能得到 其他性质吗?
刚才利用描点法作出了 和 的图像.
思考:还有其他方法可以作出它们的 图像吗?
我们现在在同一坐标系下作出 ,
和 , 的图像,并观察分析它们之间的关系.
X
Y
O
1
1
2
2
3
3
4
4
5
5
6
7
Y=log2x
Y=X
Y=2x
-1
-1
-2
●
●
●
●
●
●
●
●
●
●
从图上可以看出:
点(0,1)与点(1,0)关于直线y=x对称,点(-1, )与点( ,-1)点关于直线
y=x对称.则 上的点p(a,b)与
上的点Q(b,a)关于直线
y=x对称.
并且函数 和 互为反函数,由此,我们总结出:
㈡.利用对称性画图.
因为指数函数y=ax (a>0,且a≠ 1 )与对数函数
y=logax (a>0,且a≠ 1 )互为反函数,所以它们
的图象关于直线y=x对称。
则: 上的点p(a,b)关于y=x的对称点Q(b,a)总在 上.故利用对称点可作出 的图像.
例1求下列函数的定义域:
(1)
(2)
解 :
解 :
由
得
∴函数
的定义域是
由
得
∴函数
的定义域是
(3)
解 :
由
得
∴函数
的定义域是
应用:
和x>0,且x≠ 1
例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴考察对数函数 y = log 2x,
所以它在(0,+∞)上是增函数,于是
log 23.4<log 28.5
⑵考察对数函数 y = log 0.3 x,因为它的底数为0.3,
即0<0.3<1,所以它在(0,+∞)上是减函数,于是
log 0.31.8>log 0.32.7
因为它的底数2>1,
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
(对数函数的增减性决定于对数的底数是大于1还是小于1.
而已知条件中并未指出底数a与1哪个大,
因此需要对底数a进行讨论)
解:当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
练习: 比较下列各题中两个值的大小:
⑴ log106 log108
⑵ log0.56 log0.54
⑶ log0.10.5 log0.10.6
⑷ log1.51.6 log1.51.4
<
<
>
>
例3 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 .
解: ⑴ ∵ log67>log66=1
log20.8<log21=0
说明:利用对数函数的增减性比较两个对数的大小.
当“底真”不同不能直接进行比较时,可在两个对数中间插入一 个“桥梁”(如1或0等),间接比较上述两个对数的大小.
提示 : log aa=1
提示: log a1=0
log76<log77=1
∴ log67>log76
⑵ ∵ log3π>log31=0
∴ log3π>log20.8
图
象
性
质
对数函数y=log a x (a>0, a≠1)
指数函数y=ax (a>0,a≠1)
(4) a>1时, x<0,00,y>1
01;x>0,0(4) a>1时,01,y>0
00; x>1,y<0
(5) a>1时, 在R上是增函数;
0(5) a>1时,在(0,+∞)是增函数;
0(3)过点(0,1), 即x=0 时, y=1
(3)过点(1,0), 即x=1 时, y=0
(2)值域:(0,+∞)
(1)定义域:R
(1)定义域: (0,+∞)
(2)值域:R
y=ax
(a>1)
y=ax
(0x
y
o
1
y=logax
(a>1)
y=logax (0x
y
o
1
(2)看见函数式想图像,结合图像记性质。
(1) 类比记忆指数函数和对数函数。
比较大小:
(1)
(2)
提示:此种比较大小属于“同真”.
习题3-5 3,4
对数函数的图像和性质
一.复习对数函数的概念
定义: 函数 y = loga x (a>0,且a≠ 1 )
叫做对数函数.,其中 x是自变量,
函数定义域是( 0 , +∞)。
图 象
性 质
y
x
0
y=1
(0,1)
y=ax
(a>1)
y
x
(0,1)
y=1
0
y=ax
(0
值 域 :
恒 过 点:
在 R 上是单调
在 R 上是单调
a>1
0
( 0 , + ∞ )
( 0 , 1 ) ,即 x = 0 时, y = 1 .
增函数
减函数
指数函数 的图像及性质
当 x > 0 时,y > 1.
当 x < 0 时,. 0< y < 1
当 x < 0 时,y > 1;
当 x > 0 时, 0< y < 1。
对称性: 和 的图像关于y轴对称.
x
Y=log2x
…
…
1/4
1/2
1
2
4
…
…
-2
-1
0
1
2
x
y
o
1 2 3 4 5 6 7 8
1
2
3
-1
-2
-3
Y=log2x
①.描点画图.
●
●
●
●
㈠作 和 的图像
x
Y=log1/2x
…
…
…
…
-3
1/8
1/4
1/2
1
2
4
8
-2
-1
0
1
2
3
x
y
o
1 2 3 4 5 6 7 8
1
2
3
-1
-2
-3
Y=log1/2x
②.
O
X
Y
1
2
3
4
5
6
7
8
9
1
2
3
-1
-2
-3
Y=log2x
Y=log1/2x
将两图放入同一坐标系下观察:
三.对数函数的性质:
现在我们同样利用描点法在同一坐标系
下作出 和
的图像,观察图像并
归纳总结性质.
4
3
2
1
-1
-2
-3
2
4
6
8
10
y=log2x
y=log3x
x
y
O
a>1
0
性质
定义域: 值域:R
过点(1,0),即x=1时,y=0
x>1时,y>0
0
x>1时,y<0
在(0,+ 上是增函数
在(0,+ 上是减函数
x
1
Y
O
Y=logax
x
Y
O
1
Y=logax
4
3
2
1
-1
-2
-3
2
4
6
8
10
y=log2x
y=log3x
x
y
O
总结其它性质:
(1)y=logax (a>0,且a≠ 1 )与y=log1/ax (a>0,且a≠ 1 ) 的图像关于x轴对称。
(2)对数函数是非奇非偶函数。
考虑:根据作出的图像,还能得到 其他性质吗?
刚才利用描点法作出了 和 的图像.
思考:还有其他方法可以作出它们的 图像吗?
我们现在在同一坐标系下作出 ,
和 , 的图像,并观察分析它们之间的关系.
X
Y
O
1
1
2
2
3
3
4
4
5
5
6
7
Y=log2x
Y=X
Y=2x
-1
-1
-2
●
●
●
●
●
●
●
●
●
●
从图上可以看出:
点(0,1)与点(1,0)关于直线y=x对称,点(-1, )与点( ,-1)点关于直线
y=x对称.则 上的点p(a,b)与
上的点Q(b,a)关于直线
y=x对称.
并且函数 和 互为反函数,由此,我们总结出:
㈡.利用对称性画图.
因为指数函数y=ax (a>0,且a≠ 1 )与对数函数
y=logax (a>0,且a≠ 1 )互为反函数,所以它们
的图象关于直线y=x对称。
则: 上的点p(a,b)关于y=x的对称点Q(b,a)总在 上.故利用对称点可作出 的图像.
例1求下列函数的定义域:
(1)
(2)
解 :
解 :
由
得
∴函数
的定义域是
由
得
∴函数
的定义域是
(3)
解 :
由
得
∴函数
的定义域是
应用:
和x>0,且x≠ 1
例2 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5
⑵ log 0.31.8 , log 0.32.7
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴考察对数函数 y = log 2x,
所以它在(0,+∞)上是增函数,于是
log 23.4<log 28.5
⑵考察对数函数 y = log 0.3 x,因为它的底数为0.3,
即0<0.3<1,所以它在(0,+∞)上是减函数,于是
log 0.31.8>log 0.32.7
因为它的底数2>1,
⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
(对数函数的增减性决定于对数的底数是大于1还是小于1.
而已知条件中并未指出底数a与1哪个大,
因此需要对底数a进行讨论)
解:当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
练习: 比较下列各题中两个值的大小:
⑴ log106 log108
⑵ log0.56 log0.54
⑶ log0.10.5 log0.10.6
⑷ log1.51.6 log1.51.4
<
<
>
>
例3 比较下列各组中两个值的大小:
⑴ log 67 , log 7 6 ; ⑵ log 3π , log 2 0.8 .
解: ⑴ ∵ log67>log66=1
log20.8<log21=0
说明:利用对数函数的增减性比较两个对数的大小.
当“底真”不同不能直接进行比较时,可在两个对数中间插入一 个“桥梁”(如1或0等),间接比较上述两个对数的大小.
提示 : log aa=1
提示: log a1=0
log76<log77=1
∴ log67>log76
⑵ ∵ log3π>log31=0
∴ log3π>log20.8
图
象
性
质
对数函数y=log a x (a>0, a≠1)
指数函数y=ax (a>0,a≠1)
(4) a>1时, x<0,0
0
0
(5) a>1时, 在R上是增函数;
0
0
(3)过点(1,0), 即x=1 时, y=0
(2)值域:(0,+∞)
(1)定义域:R
(1)定义域: (0,+∞)
(2)值域:R
y=ax
(a>1)
y=ax
(0
y
o
1
y=logax
(a>1)
y=logax (0
y
o
1
(2)看见函数式想图像,结合图像记性质。
(1) 类比记忆指数函数和对数函数。
比较大小:
(1)
(2)
提示:此种比较大小属于“同真”.
习题3-5 3,4
